1. Opis ćwiczenia.

1. opis teoretyczny:

Ćwiczenie polega na sprawdzeniu zasady zachowania energii mechanicznej, jak również wyznaczaniu momentu bezwładności
bryły sztywnej. W ćwiczeniu używa się kuli staczającej się z równi pochyłej. Ruch ten jest złożony z ruchu postępowego i obrotowego bryły sztywnej. Energia potencjalna kuli znajdującej się na wysokości h zamienia się całkowicie u podstawy równi, gdzie h = 0, na energię kinetyczną ruchu postępowego i obrotowego. Wyrażone to jest równaniem wynikającym z zasady zachowania energii:

(1)

gdzie:

- masa kulki,

- przyspieszenie ziemskie,

- wysokość równi,

- prędkość końcowa kulki,

- moment bezwładności kulki,

- prędkość kątowa.

Na podstawie tej równości należy wyznaczyć moment bezwładności
kuli i porównać z

wartością wyliczoną z zależności:

(2)

gdzie:
- promień kulki.

W celu uproszczenia przekształceń równania (l), podstawić
, stąd:

(3)

W celu określenia prędkości
, należy rozważyć co wywołuje przyspieszenie środka masy a.

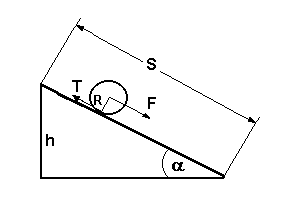
gdzie:

- siła spychająca,

- siła tarcia,

- przyspieszenie środka masy,

- kąt nachylenia równi,

- przyspieszenie kątowe.

Podstawiając do (4) otrzymamy:

stąd:

gdzie: S- długość równi

(5)

Podstawiając wartość uzyskaną w równaniu (5) do równania (3) otrzymamy:

stąd:

(6)

2. przebieg ćwiczenia:

Pomiary zostały wykonane przy dwóch różnych wysokościach dla czterech różnych kul. Droga S ma wartość stałą (nie zmienia się wraz ze zmianą wysokości h) i wynosi 3,3 [m], podana jest z dokładnością ± 1 [cm]. Pomiar czasu t staczania się kuli został zmierzony automatycznie za pomocą elektronicznego czasomierza. Ze względu na zwiększenie dokładności wyznaczania czasu t, wartość ta została zmierzona dziesięć razy dla każdej z kul przy dwóch różnych wysokościach.

2. Tabele pomiarowe.

1. 1 kula (plastikowa):

2. 2 kula (drewniana):

3. 3 kula (mała metalowa):

4. 4 kula (duża metalowa):

3. Obliczenia i dyskusja błędów.

Δh = 0,002 [m];

ΔR = 0,002 [m];

Δm = 0,05 [g];

ΔS = 0,01 [m]

- doświadczalnie wyznaczony moment bezwładności

- teoretyczny moment bezwładności

1. dla 1 kuli:

	dla h = 40 [cm]	dla h = 60 [cm]
ts	3,33	2,68
[s]
ts			0,02	0,01
[s]
C	1,00	0,94
C	0,02	0,02
Id *10^-7	8,58	8,08
[kg * m^2]
It *10^-7			3,43	3,43
[kg * m^2]
Id *10^-7			2,28	2,09
[kg * m^2]
It *10^-7			0,83	0,83
[kg * m^2]

2. dla 2 kuli:

	dla h = 40 [cm]	dla h = 60 [cm]
ts	2,79	2,27
[s]
ts			0,01	0,01
[s]
C	0,40	0,40
C	0,01	0,01
Id *10^-5	1,48	1,46
[kg * m^2]
It *10^-5			1,46	1,46
[kg * m^2]
Id *10^-5			0,29	0,28
[kg * m^2]
It *10^-5			0,26	0,26
[kg * m^2]

3. dla 3 kuli:

	dla h = 40 [cm]	dla h = 60 [cm]
ts	2,85	2,31
[s]
ts			0,02	0,01
[s]
C	0,47	0,45
C	0,01	0,01
Id *10^-5	4,80	4,68
[kg * m^2]
It *10^-5			4,17	4,17
[kg * m^2]
Id *10^-5			1,10	1,04
[kg * m^2]
It *10^-5			0,83	0,83
[kg * m^2]

4. dla 4 kuli:

	dla h = 40 [cm]	dla h = 60 [cm]
ts	2,81	2,28
[s]
ts			0,02	0,002
[s]
C	0,42	0,40
C	0,01	0,01
Id *10^-4	1,34	1,28
[kg * m^2]
It *10^-4			1,27	1,27
[kg * m^2]
Id *10^-4			0,25	0,22
[kg * m^2]
It *10^-4			0,20	0,20
[kg * m^2]

4. Wnioski.

Jak można zauważyć dla wszystkich kul oprócz pierwszej, współczynnik C wyliczony z zależności (6), jest w przybliżeniu równy współczynnikowi ze wzoru na
. Otrzymana niezgodność tej wartości dla pierwszej kuli, jest spowodowana jej niedużą masą a także niewielkimi wymiarami. Zjawisko to potwierdziło prawdziwość twierdzenia o momencie bezwładności bryły sztywnej w ruchu obrotowym, z którego wynika, że jest on zależny od masy i wymiarów bryły.

W ćwiczeniu udało się uzyskać bardzo zbliżone wartości doświadczalnego
i teoretycznego
momentu bezwładności bryły w ruchu obrotowym.

6

Rys. 1. Ruch bryły sztywnej po równi pochyłej

---