Inżynieria środowiska
I ROK
|
|
24.04.2012 |
Ćwiczenie numer 10 |
Badanie ruchu bryły sztywnej na równi pochyłej. |
|
Wprowadzenie
Równia pochyła - jedna z najdawniej używanych maszyn prostych. Przykładem równi jest dowolna pochylnia. Równia to płaska powierzchnia nachylona pod pewnym kątem do poziomu, po której wciągany lub spuszczany jest dany przedmiot. Wyznaczanie parametrów ruchu ciała po tej powierzchni (przede wszystkim wyznaczenie przyspieszenia) nazywane jest zagadnieniem równi.
W ćwiczeniu bryłą sztywną jest kula staczająca
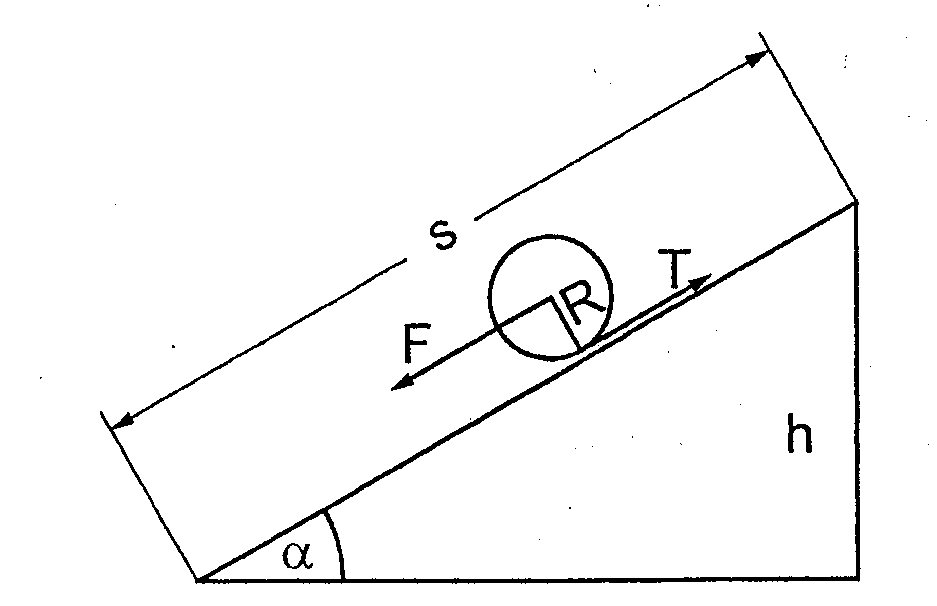
się po równo pochyłej. Ruch kuli złożony jest z ruchu postępowego i obrotowego.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
gdzie:
F - siła spychająca
T - siły tarcia
a - przyspieszenie środka masy
α - kąt nachylenia równi
ε - przyspieszenie kątowe
![]()
Podstawiając otrzymamy:
![]()
![]()
![]()
oraz ![]()
stąd
![]()
![]()
gdzie: s - długość równi
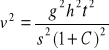
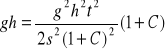
![]()
Tabela pomiarów
Katarzyna Głowska
h1 [m] |
t [s] |
h2 [m] |
t [s] |
||||
|
kulka 1 m=......g |
kulka 2 m=......g |
kulka 3 m=......g |
|
kulka 1 m=......g |
kulka 2 m=......g |
kulka 3 m=......g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Tabela załączona na zdjęciu)
3. Obliczenia
Dla wysokości 0,6m Czas ( t [s] )
Kulka o masie 2,48g o średnicy 37mm Kulka o masie 68,98g o średnicy 47mm Kulka o masie 286,2g o średnicy 41mm
2,743 2,242 2,261
2,700 2,255 2,256
2,677 2,246 2,270
2,692 2,247 2,253
2,711 2,237 2,276
2,671 |
|
Dla wysokości 0,45m Czas ( t [s] )
Kulka o masie 2,48g o średnicy 37mm Kulka o masie 68,98g o średnicy 47mm Kulka o masie 286,2g o średnicy 41mm
3,098 2,613 2,640
3,141 2,614 2,625
3,176 2,607 2,624
3,159 2,616 2,663
3,169 2,619 2,639
3,132 2,618 2,637
3,180 2,599 2,640
3,173 2,601 2,641
3,109 2,614 2,627
3,161 2,612 2,637
Czas średni
3,150 2,611 2,637
|
Dla wysokości 0,6m:
Dla wysokości 0,45m:
Moment bezwładności:
h=0,6m |
Kula 1 |
Kula 2 |
Kula 3 |
h=0,45m |
Kula 1 |
Kula 2 |
Kula 3 |
C= |
0,94 |
0,36 |
0,39 |
C= |
1,01 |
0,38 |
0,41 |
m= |
2,48g |
68,98g |
286,2g |
m= |
2,48g |
68,98g |
286,2g |
R= |
|
|
|
R= |
|
|
|
|
0,0008 |
0,0137 |
0,0469 |
|
0,00009 |
0,0145 |
0,0493 |
Wartości teoretyczne momentu bezwładności:
-dla kuli pełnej
-kula wydrążona cienkościenna
Kula 1 oraz 2 to kule wydrążone cienkościenne, kula 3 to kula pełna. Zatem:
Nie zależy od h |
Kula 1 |
Kula 2 |
Kula 3 |
m= |
2,48g |
68,98g |
286,2g |
R= |
|
|
|
|
0,0006 |
0,0254 |
0,0481 |
4. Rachunek niepewności pomiarowych
|
KULA 1 |
KULA 2 |
KULA 3 |
|
0,004096 |
0,000025 |
0,000064 |
|
0,000441 |
0,000064 |
0,000169 |
|
0,000004 |
0,000001 |
0,000001 |
|
0,000169 |
0,000000 |
0,000256 |
|
0,001024 |
0,000100 |
0,000049 |
|
0,000064 |
0,000000 |
0,000049 |
|
0,003969 |
0,000016 |
0,000064 |
|
0,000900 |
0,000036 |
0,000049 |
|
0,000100 |
0,000009 |
0,000025 |
|
0,000196 |
0,000009 |
0,000729 |
Suma [s]: |
0,006867 |
0,000235 |
0,001391 |
|
KULA 1 |
KULA 2 |
KULA 3 |
|
0,002704 |
0,000004 |
0,000009 |
|
0,000081 |
0,000009 |
0,000144 |
|
0,000676 |
0,000016 |
0,000169 |
|
0,000081 |
0,000025 |
0,000676 |
|
0,000361 |
0,000064 |
0,000004 |
|
0,000324 |
0,000049 |
0 |
|
0,000900 |
0,000144 |
0,000009 |
|
0,000529 |
0,000100 |
0,000016 |
|
0,001681 |
0,000009 |
0,000100 |
|
0,000121 |
0,000001 |
0 |
Suma [s]: |
0,004754 |
0,000417 |
0,001118 |
Obliczam niepewność pomiarową u(C) ze wzoru:
Dla wysokości 0,6m
Dla kuli 1
Dla kuli 2
Dla kuli 3
Dla wysokości 0,45
Dla kuli 1
Dla kuli 2
Dla kulki 3
Obliczam niepewność pomiarową u(Id) ze wzoru:
Dla wysokości 0,6m
Dla kuli 1
Dla kuli 2
Dla kuli 3
Dla wysokości 0,45m
Dla kuli 1
Dla kuli 2
Dla kuli 3
Obliczam niepewność pomiarową u(It) ze wzoru:
Dla kuli 1
Dla kuli 2
Dla kuli 3
5.Wnioski
Porównanie wartości doświadczalnych oraz teoretycznych:
|
Wartości doświadczalne h=0,6m |
Wartości teoretyczne |
|
Wartości doświadczalne h=0,45m |
Wartości teoretyczne |
Kula 1 |
|
|
|
0,00009 |
|
Kula 2 |
|
|
|
|
|
Kula 3 |
|
|
|
0,0493 |
|
Zadaniem było wykonanie odpowiednich pomiarów takich jak: czas staczania się kul, zmierzenie ich mas oraz promieni. Wyniki były potrzebne do obliczenia momentu bezwładności dla każdej kuli z osobna. Otrzymane momenty bezwładności dla poszczególnych kul różniły się od siebie w zależności od ich masy, rozmiarów i wysokości początkowej staczania. Porównując momenty kul wyliczone za pomocą wzorów z ich wartościami teoretycznymi zauważamy że pomiar 3 kuli wyszedł doskonale. Wyniki pozostałych dwóch kul różnią się od wartości teoretycznych. Przyczyną takiego błędu może być: niedokładne ustawienie początkowe kuli lub niedokładne odczyty pomiarów.
Wyszukiwarka
Podobne podstrony:
1. Badanie ruchy bryły sztywnej po równi pochyłej, Badanie ruchu bryły sztywnej na równi pochyłej.,
Badanie ruchu bryły sztywnej po równi pochyłej2
Badanie ruchu bryły sztywnej po równi pochyłej, Studia, laborki fizyka (opole, politechnika opolska)
Badanie ruchu bryły sztywnej na równi pochyłej
Badanie ruchu bryły sztywnej na równi pochyłej
Badanie ruchu bryły sztywnej na równi pochyłej. , Ćwiczenie
Badanie ruchu bryły sztywnej na równi pochyłej
18. Badanie ruchu bryły sztywnej na równi pochyłej
Badanie przemian energii mechanicznej na równi pochyłej POPRAWIONE (2)
Badanie ruchu obrotowego bryły sztywnej, CW6, Temat: Pomiar czujnikiem indykcyjnym.
Ćw 10;?danie ruchu bryły sztywnej na równi pochyłej
Badanie ruchu obrotowego bryły sztywnej i wyznaczenie momentu?zwładności przyrządu (wahadło Obe (2)
10. Ruch po równi pochyłej, Fizyka - Lekcje
Bryła sztywna na równi pochyłej, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
Bryła sztywna na równi pochyłej
Ruchy i wspólnoty w Kościele po Drugim Soborze Watykańskim
więcej podobnych podstron