20./KBI

SCHEMATY STATYCZNE i KOMBINACJE OBCIĄŻEŃ W ZBIORNIKACH NA MATERIAŁY SYPKIE I CIECZE

Silosy są to budowle przeznaczone do tymczasowego składowania materiałów sypkich, utworzone z jednego lub wielu komo w których uwzględnia się wpływ tarcia składowanego materiału na wartości parcia tego materiału na ściany i dno.

Bunkry są to budowle przeznaczone do tymczasowego składowania materiałów sypkich, których głębokości składowania są małe w stosunku do wymiarów ich rzutu poziomego.

Parcie składowanego materiału występujące po napełnieniu komory silosu zależy od:

• cech składowanego materiału

• stosunków wymiarów geometrycznych komory

• wielkości współczynnika tarcia materiału o ściany komory.

Parcie to ma charakter statyczny.

Istnieje kilka metod obliczania tego parcia, najbardziej powszechną w użyciu jest metoda Janssena według której:

• parcie poziome p_h,nap zwiększa się wyraźnie tylko do pewnej wysokości napełnienia dążąc asymptotyczne do wartości stałej;

• parcie pionowe p_v,nap jest znacznie mniejsze od ciężaru składowanego materiału.

Zjawisko to jest spowodowane siłami tarcia p_t,nap występującymi na obwodzie komory, wskutek czego część ciężaru zawartości komory przenosi się na ściany komory. Głównym założeniem Janssena było przyjęcie stałego stosunku pomiędzy poziomym i pionowym parciem materiału.

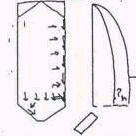
Parcie składowanego materiału podczas opróżniania komory silosu zależy od :

• sposobu i szybkości opróżniania komory

• układu konstrukcyjnego silosu (baterii komór silosowych)

• , układu konstrukcyjnego samej komory

• liczby i usytuowania otworów wysypowych

• parametrów technicznych składowanego materiału

• technologii użytkowania silosu

Parcie to ma charakter dynamiczny - stosujemy współczynnik dynamiczny o wartościach od l do 2.

Parcie poziome p_h,op określa się go jako superpozycję parcia wyznaczonego dla całej powierzchni ściany oraz parcia równomiernego, działającego pierścieniowo p_h,op,p (to parcie ma wpływ na siły równoleżnikowe, a wyznacza się go w zależności od rodzaju przepływu materiału w komorze).

Parcie pionowe p_v,op materiału składowego przyjmuje się równe parciu pionowemu występującemu w komorze po jej napełnieniu

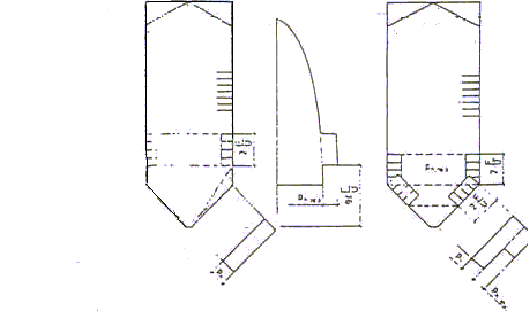
Parcie materiału sypkiego na dno komory:

Parcie na lej silosu sprowadza się do wyznaczenia parcia normalnego p_n oraz parcia stycznego p_t działających równomierne na ściany leja. Na oba te parcia ma wpływ materiału wypełniającego lej oraz parcie materiału znajdującego się w komorze działające na górną poziomą powierzchnie leja.

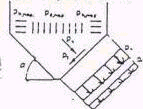
W płaszczyźnie poziomej w ścianach komór występują wewnętrzne siły rozciągające od parci poziomego i momenty zginające - w przypadku baterii silosowych - od sąsiednich komór.

W płaszczyźnie pionowej w ścianach komór występują wewnętrzne siły ściskające od:

• ciężaru przekrycia wraz z galerią nadsilosową oraz obciążenia zewnętrzne (np. śnieg);

• ciężaru własny ścian:

• sil tarcia materiału zasypowego o ścian

i momenty zginające od sil poziomych przy podporach i ciężaru leja wraz z parciem na niego składowanego materiału- gdy konstrukcja leja obciąża ściany komór.

Gdy ściany oparte komór są na słupach bądź fragmentach ścian przekazujących obciążenia pionowe na fundamenty, w dolnych częściach pracują one jak belki-ściany. W przybliżeniu przyjmuje się obliczeniową ich wysokość równą rozstawom słupów w świetle otworów dolnych ścian. Za obciążenia tych belek-ścian przyjmuje się:

• u góry- siły N na wysokości' 0.5 L belki ściany

• u dołu- siły N' obciążające belkę-ścianę od dolnej krawędzi do wysokości 0,5 L

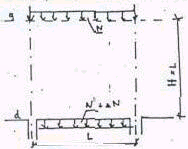
Obliczanie dna silosu:

l. Dno w postaci leja o kształcie odwróconego stożka pracuje na siły rozciągające w kierunku radialnym (wzdłuż tworzącej stożka) oraz w kierunku pierścieniowym (w płaszczyźnie poziomej). Wielkość tych sil można wyznaczyć z warunku równowagi sil działających na myślowo odciętą część stożkowego leja w poziomie obliczanych sil wewnętrznych.

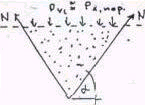
Na górną powierzchnię myślowo odciętej części leja działa parcie pionowe p_d,nap

Wielkość tego parcia wraz z ciężarem odciętej części leja G musi być zrównoważona wewnętrznymi siłami radialnymi N działającymi na obwodzie ściany stożka wzdłuż jego tworzącej,

Momenty zginające w ścianie leja stożkowego poza strefą przypodporową (zawieszenie na ścianach pionowych, komory silosowej) są na ogól niewielkie,

Przy krawędzi powłoki dennej i walcowej moment, zginający w płaszczyźnie pionowej osiąga niekiedy dużą wartość, zasięg jego działania w powłoce walcowej jest jednak niewielki.

Przy obliczaniu leja należy również mieć na uwadze siły odrywające lej od korpusu komory. Wielkość tych sił, przypadających na jednostkę obwodu komory, oblicza się dzieląc całkowite obciążenie leja przez jego obwód u nasady, przy czym na całkowite obciążenie składa się tu obciążenie górnej powierzchni leja od parcia p_d,nap i ciężar własny leja wraz z materiałem sypkim w jego wnętrzu .

2.Lej silosu o kształcie odwróconego ostrosłupa pracuje na siły rozciągające w kierunkach odpowiadających pionowym i poziomym płaszczyznom przekrojów leja. jak również na momenty, które zginają trójkątne bądź trapezowe boczne ściany leja.

Wielkości sil rozciągających R działających w płaszczyźnie poziomej, obliczane są niekiedy jak dla poziomej ramy zamkniętej, jako oddziaływanie przyległych ścian. Również i poziome momenty zginające w ścianach leja bywają często wyznaczane jak dla zamkniętej ramy. Obliczenia takie nie odpowiadają jednak rzeczywistej pracy ścian lejów ostrosłupowych gdyż ściany te pracują jako płyty dwukierunkowo zginane. Dlatego też wielkości te powinny być określane lak samo jak dla płyt trójkątnych bądź trapezowych zamocowanych na obwodzie. Obciążenia tych płyt można przyjmować za równomierne. Otrzymany dla płyt moment zamocowania działający ca górnej krawędzi poziomej, która monolitycznie łączy obliczany lej ze ścianami pionowymi komory, może być przyjęty do wymiarowania wówczas gdy jego wartość będzie odpowiadała wartości momentu zamocowania dolnej krawędzi ściany komory w ścianie leja. Gdy wartości tych momentów różnią się wtedy na podstawie wielkości tej różnicy można określić stopień sprężystego zamocowania na poziomej krawędzi oraz wykonać poprawkę w obliczeniach. Ściany takich lejów zbroi się dwukierunkowo.

Słupowe podpory komór oblicza się na podłużne siły powstające od ciężaru materiału zasypowego, własnego ciężaru konstrukcji i działania wiatru, jak również na momenty zginające od wiatru.

W przypadku baterii silosowej wpływ komory obciążonej na komory przyległe i dalej położone w układzie więcej niż trzy (w każdym kierunku) można uwzględnić wpływ komory tylko na komory najbliższe rozpatrując jedynie układ 9- komorowy.

Im większą liczba boków ma przekrój poziomu komory, tym mniejsze są w nich momenty zginające, a większe siły podłużne.

Najbardziej ekonomiczne są komory okrągłe, gdyż w ich ścianach powstają na ogól tylko pierścienie rozciągające siły osiowe które powstają od poziomego parcia materiału

Z punktu widzenia pracy statycznej rozróżniamy typy bunkrów:

• bunkry-leje

• bunkry niskie

• bunkry wysokie

Parcie materiału sypkiego w bunkrach

Od materiałów przechowywanych mamy statyczne oddziaływanie obciążeń. Natomiast dynamiczne oddziaływanie występuje podczas załadunku i opróżniania bunkrów.

Przy napełnianiu bunkra należy uwzględnić współczynnik dynamiczny (przez który przemnażane jest parcie stateczne) o wartościach 1<
<1.5 w zależności od stosunku objętości jednostkowego wsypu materiału do użytkowanej objętości komory bunkra (zarówno ścian jak i leja).

Siły rozciągające ściany bunkra są wywołane składową normalną g_n ciężaru własnego pochyłych ścian leja oraz jednostkowym parciem normalnym p_n materiału sypkiego wypełniającego bunkier (powodującego mimośrodowe rozciąganie).

Siły N rozciągające ściany leja oraz ściany górnej części bunkra określa się kolejno dla wydzielonych pasów o szerokości l m przy obliczaniu sił w ścianach leja rozpatruje się pas ściany o szerokości jednego metra w kładzie (nie w rzucie).

Gdy na krawędzi połączenia ścian pionowych bunkra z ukośnymi ścianami jego leja wykonuje się obwodowe belki o dużym przekroju poprzecznym lub też podpierające je w narożach słupy znacznie ograniczające podłużne odkształcenia tych belek poziome siły podłużne N' i N'' w ścianach w pobliżu tych belek będą mniejsze niż te obliczone powyżej; jeżeli można założyć że belki w ogolę nic odkształcają się w kierunkach podłużnych, siły N' i N'' w ścianach przy tych krawędziowych belkach będą równe zeru. W tym przypadku siły można obliczyć przyjmując obciążenie normalne - wywołujące te siły - ograniczone do, powierzchni działania według podziału płyt dwusiecznymi kątów krawędziowych.

Zarówno w ścianach leja, jak i dolnej części pionowych ścian bunkra występują także rozciągające siły działające wzdłuż pochyłości ścian, tj. w płaszczyznach stoku. Siły te dążą do oderwania leja i można je wyznaczyć rozpatrując kolejno równowagę sił w poziomych przekrojach bunkra. Przyjmujemy siły N''' i równomiernie rozłożone na obwodzie badanego przekroju, należy jednak pamiętać, ze w rzeczywistości siły N''' rozkładają się nierównomiernie na obwodzie przekroju i mają większą wartość przy narożach leja, gdyż naroża oznaczają się znacznie większą sztywnością niż środkowa część płaszczyzn.

Lej w płaszczyźnie pionowej obliczamy jak belkę-ścianę obciążoną na krawędzi od ciężaru własnego i materiału składowanego.

Obliczanie ścian bunkra na miejscowe zginanie:

Bunkier składa się z szeregu elementów płytowych (leje o kształcie figury obrotowej stosuje się rzadko), z których każdy powinien być obliczony na działanie miejscowego zginania w założeniu, że stanowi samodzielną całość. Ściany leja mają kształt trapezowy, przy czym w przypadku, gdy długość mniejszej podstawy nic przekracza 0,25 długości większej podstawy, mogą one być liczone jako płyty trójkątne (przy zastępczej wysokości trójkąta).

Płyty ograniczające lej (dolna część bunkra) przyjmuje się zazwyczaj jako utwierdzone na krawędziach przecięcia się z sąsiednimi płytami leja, natomiast na pozostałych krawędziach przyjęcie sposobu podparcia i zamocowania musi być każdorazowo uzasadnione stopniem sztywności przylegającego elementu (w miejscu styku z pionową ścianą bunkra) lub też wielkością otworu i nieodkształcalnością jego obrzeża (w miejscu przylegania do otworu leja).

Przy lejach o prostokątnym (nie kwadratowym) przekroju poziomym na każdej z krawędzi leja w sąsiednich płytach uzyskuje się z obliczeń różne momenty utwierdzenia, jednak można dla obu sąsiednich płyt przyjmować jeden moment utwierdzenia równy średniej arytmetycznej obu momentów.

Płyty ścian pionowych bunkra wysokiego należy obliczać jako płyty prostokątne w warunkach brzegowych dostosowanych do rzeczywistego układu konstrukcyjnego.

Górna krawędź pionowej płyty bunkra może być swobodna (co występuje najczęściej), swobodnie podparta lub częściowo, a nawet niekiedy całkowicie zamocowana.

Pionową płytę ścienną bunkra można przyjmować jako wspornikową w przypadku, gdy jej wysokość h nie przekracza połowy długości ściany. Gdy wysokość pionowej ściany bunkra jest przeszło dwukrotnie większa od jej długości, można pionowe płyty obliczać u góry (na odcinku, w którym praktycznie me występują wpływy zamocowania ściany w dnie) jako poziomą ramę zamkniętą.

Jeśli w rzucie poziomym bunkier ma kształt prostokąta o znacznej różnicy długość boków przy czym wysokość h pionowych ścian w stosunku do długości większego boku b waha się w granicach 0.5<b/h<2 można przy obliczani momentów utwierdzenia na pionowych krawędziach narożnych bunkra arytmetyczną momentów w utwierdzeniu obu sąsiadujących ścian; należy wówczas zwiększyć odpowiednio moment przesłony w dłuższej ścianie, gdyż moment utwierdzenia tej ściany przyjmuje się w tym przypadku zmniejszony.

Bunkry-leje oblicza się jako układy przestrzenne w dwóch następujących charakterystycznych przekrojach:

• w przekroju tuż obok podpór - na działanie skoncentrowanych w tym miejscu sił rozciągających oraz poprzecznych sil ścinających:

• w połowie rozpiętości ściany leja, pracującej jako trójkątna belka - ściana- gdzie w dolnej jej części sumują się siły rozciągające wywołane parciem materiału sypkiego oraz siły wywołane pracą belki-ściany (przy pracy trójkątnej belki-ściany w górnej jej części powstają siły ściskające, natomiast w dolnej rozciągające.

W oparciu o ten wykres naprężeń oblicza się wewnętrzne siły rozciągające, które należy zsumować z wewnętrznymi siłami wynikającymi z parcia materiału magazynowanego w leju. Wewnętrzne siły ściskające, powstające w górnej części trójkątnej belki- ściany, należy zsumować z milami rozciągającymi w leju.

Bunkry niskie należy obliczać z uwzględnieniem pracy pionowych ścian, które wspólnie z górną częścią leja pracują jako belki-ściany. Szczególnie duże znaczenie mają te ściany wtedy, gdy wysokość ich jest zbliżona do połowy rozpiętości.

Obliczając te bunkry na zginanie należy:

• określić rozciągające siły występujące w połowie rozpiętość przęsła ścian bunkra

• Sprawdzić pionową ścianę w licu słupa na działanie głównych naprężeń rozciągających, czyli ścinania.

Zbiorniki na materiały płynne ze względu na usytuowanie dzielimy na: podziemne, powierzchniowe (spoczywają bezpośrednio na gruncie lub są częściowo zagłębione), nadziemne (na słupach lub innych konstrukcjach pracujących niezależnie od konstrukcji zbiornika, lub są umieszczane na wieżach).

Pod względem geometrii dzielimy na : o rzucie prostokątnym, o kształcie bryły obrotowej z pionową osią obrotu (przekrój kołowy).

W przypadku zbiorników zagłębionych w gruncie na znaczną głębokość, przy wymiarach poziomych kilkakrotnie większych od wysokości, ściany boczne zbiorników można projektować jako ściany oporowe kątowe lub żebrowo - płytowe z dozbrojeniem naroży jeśli ma to uzasadnienie ekonomiczne).

Istotne jest tu zapewnienie szczelności.

Obciążenie od cieczy - hydrostatyczne:

W zbiornikach prostokątnych ściany mogą być połączone z dnem w sposób sztywny lub przegubowy bądź też oddzielone od dna szczeliną dylatacyjną (zależnie od konstrukcji płyty dna). Górne krawędzie ścian w zbiornikach zamkniętych są połączone w sposób przegubowy lub sztywny z konstrukcją przekrycia a w zbiornikach otwartych krawędzie mogą być swobodnie podparte lul opierać się na poziomej ramie-

W zbiornikach wielokomorowych ściany pionowe połączone są ze sobą monolitycznie, tworząc węzły mogące przenieść powstające w nich momenty zamocowania.

Obliczanie ścian zbiornika jako zespołu płyt wydzielonych: metodę tą stosuje się gdy długość ściany zbiornika otwartego, czyli nie podpartego u góry, jest mniejsza od swojej trzykrotnej wysokości, a w przypadku zbiornika podpartego na górnej krawędzi -gdy długość jest mniejsza od swojej dwukrotnej wysokości; w tych przypadkach płyty można uważać za dwukierunkowo zbrojone. Gdy te warunki nie są spełnione można uważać płytę za jednokierunkowo zbrojoną, uwzględniając jednak zamocowania na jej krawędziach pionowych

W przypadku zbiorników podziemnych występuje zginanie płyty dennej odporem gruntu i parciem wody gruntowej oraz działają siły od:

• ciężaru własnego pionowych ścian

• ciężaru przekrycia zbiornika

• obciążenie przekrycia gruntem

• obciążenie użytkowe powierzchni gruntu

Z oddziaływania ścian na dno (krawędź dolna) wynika, że w środkowej części płyty dennej występują siły rozciągające, natomiast w bocznych częściach położonych blisko naroży płyta denna jest ściskana.

Siły poprzeczne w ścianach, zbiornika będące oddziaływaniem wzajemnych sąsiadujących ścian (i jednocześnie będące siłami podłużnymi w ścianach prostopadłych) od parcia cieczy bądź również parcia ziemi - przy zbiornikach podziemnych, wraz z momentami zginającymi wywołują mimośrodowe rozciąganie (bądź ściskanie), na które wymiaruje się ściany zbiornika.

W zbiornikach o dużych długościach ścian w porównaniu z ich wysokością ściany boczne pracują głównie w płaszczyznach pionowych jak wsporniki zamocowane w fundamentowej podłużnej podstawie płytowej (przy swobodnej górnej krawędzi). Głównym zbrojeniem jest tu zbrojenie pionowe ścian. W narożach połączeń prostopadłych do siebie ścian występują również momenty zginające w płaszczyznach poziomych-Momenty te mają dość złożony przebieg - trójkątny od cieczy lub trapezowy od gruntu z obciążonym naziomem. Można je obliczyć w sposób przybliżony jak dla trójkątnego wspornika wydzielonego przez dwie proste nachylone do krawędzi pionowej pod kątem 45°.

Gdy ściana jest zamocowana u dołu i oparta u góry na poziomej ramie, to można ją obliczać na długości jako płytę jednoprzęsłową. Górne podparcie jest sprężyste i zależy od poziomego odkształcania się ramy.

W przypadku zbiorników zamkniętych ściany boczne mają podparcie u góry przegubowe poziomo nieprzesuwne.

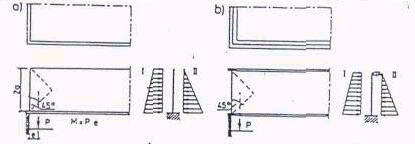
rys. Schematy obliczeniowe dwóch typów zbiorników prostokątnych otwartych o ścianach

2. o swobodnej górnej krawędzi,

3. opierających się u góry na poziomej ramie

Zbiorniki o przekroju kołowym są bardziej ekonomiczne gdyż ich boczne ściany (a czasem dno i przykrycie) pracują głównie na rozciąganie lub ściskanie osiowe

Zestawienie obciążeń następuje dla następuje dla:

- zbiorników pustych

- zbiorników pełnych

KSZTAŁTOWANIE I KONSTRUOWANIE ZASOBNIKÓW NA MATERIAŁY SYPKIE I CIECZE.

1. SILOSY

a) Ściany komory - wstępne określenie grubości można przeprowadzić mi podstawie wzoru:

t = (od 0.4 do 0.5) M^1/2

M - moment zginający w prześle od obciążeń charakterystycznych

Zbrojenie poziome tych ścian oblicza się na mimośrodowe rozciąganie tak w przekrojach przęsłowych jak i w podporowych od sił i momentów obliczeniowych, natomiast od wartości charakterystycznych należy sprawdzić ugięcie ścian, które nie powinno być większe od l\200, gdzie l - jest rozpiętością sprawdzanej ściany komory.

Pionowe ściany komór okrągłych pracują w płaszczyznach poziomych głównie na pierścieniowe siły rozciągające oraz na niewielkie momenty zginające równoleżnikowe (np. od obciążeń termicznych, obciążeń osiowo- niesymetrycznych materiału sypkiego, od miejscowego parcia poziomego działającego w czasie opróżniania komory).

Ściany wewnętrzne zbroi się zawsze dwustronnie (mogą tu wystąpić momenty zginające różnych znaków), natomiast ściany wewnętrzne o malej sile rozciągającej (w górnej części komór) mogą być zbrojone w przęsłach tylko po stronie zewnętrznej, a ściany o dużej sile rozciągającej (w dolnej części komór) muszą być również zbrojone dwustronnie. Inny ryp konstrukcji charakteryzuje się głównie symetrycznymi skosami o pochyleniu najczęściej l:3. Punkt przecinania ukośnie odgiętych prętów pokrywa się tu z zerowym punkiem przebiegu momentów zginających.

Rys. Zbrojenie fragmentu zespołu komór prostokątnych o skosach załamanych o nachyleniu 1:3

Gdy ściany pionowe opierają się bezpośrednio na słupach, wówczas słupy należy wprowadzić w ścianę na taką wysokość, aby siła przekazywana na słup nie przekroczyła nośności na docisk (na poziomej płaszczyźnie oparcia przekroju ściany na słupie) oraz na ścinanie (na bocznych pionowych płaszczyznach przenikania ściany w słup).

Ważne jest przyjęcie odpowiednich fundamentów z uwagi na duże naciski. Przyjmuje się fundamenty specjalne lub pale.

b) Lej - zbroi się obliczając przekroje poziome na rozciąganie osiowe jak w przypadku ścian komór okrągłych. W przekrojach pionowych (południkowych) poza siłami rozciągającymi występują również momenty zginające, lecz są one- poza przekrojami podporowymi- niewielkie i nie mają wpływu na grubość ścian i przekroje zbrojenia.

c) Połączenie ścian komory z dnem - w przekrojach podporowych w miejscu połączenia komory z dnem podwieszonym do jej pionowych ścian należy umieścić zbrojenie przechodzące z konstrukcji dennej w ściany komory- zbrojenie to pracuje na siłę odrywającą.

2. BUNKIER

a) Ściana pionowa -jest zbrojona ze względu na zginanie w płaszczyźnie pionowej od ciężaru własnego oraz użytkowego oraz na ich zginanie wywołane poziomym parciem materiału sypkiego.

Rys. Układ zbrojenia ściany pionowej bunkra niskiego

Rys . Zbrojenie pionowej ściany bunkra a) skrajnej b) środkowej

W ścianach o znacznej wysokości zarówno pręty pionowe jak i poziome pracują na dwukierunkowe zginanie wywołane parciem poziomym składowanego materiału

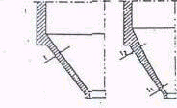
b) Lej ostrosłupowy - najczęściej stosowany w bunkrach

Rys. Zbrojenie leja ostrosłupowego prętami z odgięciami przy podporach.

Rys. Kształt i zbrojenie oporowych belek lejów opartych na słupach lub pilastrach

c) Żelbetowy tej stożkowy - stosowany głównie w silosie.

Rys. Przykład konstrukcji leja stożkowego podwieszonego do ściany komory kolistej

3. Zbiorniki na ciecze:

a) Ściany zbiornika - o wymiarach odpowiadających płytom dwukierunkowo zbrojonym ulegają rozciąganiu siłami podłużnymi oraz zmiennym na długości ściany momentom zginającym. Mogą więc wystąpić przekroje osiowo lub mimośrodowo rozciągane.

Przekroje pionowych prętów należy wyznaczyć na podstawie momentów zginających w płaszczyznach pionowych- z uwzględnieniem ściskających sił pionowych. W zbiornikach ze ścianami bocznymi zamocowanymi w dnie najwięcej prętów potrzeba w pasmach przydennych; w części górnej spełniają rolę prętów montażowych.

• ściany o dużych wymiarach w rzucie w porównaniu z wysokością pracują głównie w kierunku pionowym. W ścianach wspornikowych zbrojenie pionowe usytuowane jednostronnie - gdy na ścianę działa tylko obciążenie od cieczy, lub dwustronnie - gdy zbiornik jest zagłębiony w gruncie. W ścianie gdzie występuje oparcie na dolnej i górnej krawędzi wymiarowanie zbrojenia przeprowadza się przy dnie i w środku, gdzie występują momenty odwrotnego znaku tuż przy podporze dolnej.

b) Konstrukcja naroży pionowych - powinna zapewnić przejecie ujemnych momentów zamocowania częściowego lub pełnego.

Rys. Typowe zbrojenie pionowych narozy zbiorników a) dwóch b) trzech c) i d) czterech.

c) Połączenia ścian bocznych z dnem -jest szczególnie ważne gdyż zastosowanie przegubu bądź utwierdzenia jest uwarunkowane przede wszystkim konstrukcją dna.

Rys . Przegubowe połączenie z ława fundamentową bocznej ściany zbiornika prostokątnego

Rys. Szczegół monolitycznego połączenia bocznej ściany zbiornika z płytą denną

Rys. Dwa rodzaje dylatowania płyty dennej od bocznej ściany zbiornik prostokątnego.

23. Ogólne

Ramy, fundamenty, ściany oporowe

II.35. Ramy żelbetowe monolityczne i z elementów prefabrykowanych

Ramy to układy prętowe o prętach połączonych w sztywnych węzłach tzn. przy odkształceniu sprężystym układu kąty między stycznymi do osi odkształconych prętów zbiegających się w danym węźle nie zmieniają się oraz nie zachodzi wzajemne przesunięcie tych prętów. Węzły ram mogą być realizowane jako bez przegubowe lub przegubowe, przy czym liczba sztywnych połączeń musi być wystarczająca, zapewnić geometryczną niezmienność układu.

W ramach monolitycznych , jeśli tylko pozwalają na to miejscowe warunki gruntowe, stosuje się ogólną sztywność i niezmienność geometryczną układu.

Na terenach o niekorzystnych warunkach gruntowych konieczne jest stosowanie oddzielnych ram połączonych wzajemnie przegubowo za pomocą za pomocą elementów prętowych; jedynie jednoprzęsłowa rama przegubowa, oparta na stopach fundamentowych, jest niewrażliwa na nierównomierne osiadanie.

RYGLE - pracują na zginanie i ścinanie, przekrój zwykle prostokątny szerokość ½ do ¼ h , h co najmniej równa 1/15 rozpiętości. Otwory w ryglach należy wykonać w połowie rozpiętości (decydują siły poprzeczne). Prefabrykowane rygle współpracujące z nadbetonem - dwa typy strzemion, aby zapewnić współpracę : I typ - strzemiona dla prefabrykowanej części rygla, II typ strzemiona dla łącznej wysokości rygla po wykonaniu nadbetonu.

SLUPY - ściskane mimośrodowo ( N i M. - wynikają głównie z monolit. połącz. z ryglami i stopami), przekrój kwadratowy lub prostokątny. Prefabrykowane słupy w budynkach jednokondygnacyjnych do 7 m - przekrój prostokątny lub liniowo zmienny, powyżej 7 m dwuteowy, a w budynkach wielokondygnacyjnych przekrój kwadratowy lub prostokątny o wysokości jednej lub dwóch kondygnacji. W ramach obciążonych suwnicami wykonuje się krótkie wsporniki.

WĘZŁY, ZAŁAMANIA I NAROŻA RAM - należy tak konstruować, aby pręty zbrojeniowe rozciąganej strefy nie miały tendencji do wyrywania się - w zależności od rodzaju węzła należy wykonać odpowiednie wygięcie i zakotwienie prętów oraz stosować strzemiona.

RAMY PREFABRYKOWANE składają się z oddzielnych elementów ( słupy, rygle) scalane w ustrój ramowy na budowie lub gotowych segmentów ramowych.

Połączenia elementów. - 1) w węzłach ram dzięki czemu elementy mają mniej skomplikowany kształt, ale połączenie w przekrojach o dużych M i Q .

- 2) w miejscach występowania najmniejszych M, ale wtedy skomplikowany kształt elementów.

Połączenia powinny być tak skonstruowane, aby zapewniły ustrojowi charakter pracy ramy, powinny być możliwie proste, aby ich wykonanie nie stwarzało trudności technologicznych. Przykłady połączeń Kobiak Rozdz. 11.2.5-11.2.7.

Fundamenty żelbetowe:

• Fundamenty płytkie (bezpośrednie) - ławy, stopy, fundamenty rusztowe, płytowe, skrzyniowe (wyk. gdy grunt niejednorodne zmiennym modułem ściśliwości, duże obciążenia.)

• Fundamenty - pale, studnie, kesony - stosowane, gdy o wymaganej wytrzymałości na większej głębokości

SGN obejmuje: wypieranie podłoża przez pojedynczy fragment lub przez całą budowlę usuwisko lub zsuw fundamentu lub podłoża wraz z budowlą (posadowienie na zboczu) przesunięcie w poziomie posadowienia fundamentu lub głębszych warstwach podłoża.

SGU obejmuje: średnie osiadanie fundamentów budowli, przechylenie budowli jako całości lub jej części wydzielonej dylatacjami, wygięcie (ugięcie) budowli jako części między dylatacjami, różnica osiadań fundamentu.

Podstawowy warunek przy sprawdzaniu SGN:
lub
(1)

- obliczeniowe obciążenie działające na podstawę fundamentu w kN (uwzględniając najniekorzystniejsze zestawienie oddziaływań od obciążenia stałego i zmiennego, parcia gruntu, wód gruntowych, obciążenie od sąsiednich fundamentów)

- obliczeniowy opór graniczny podłoża gruntowego przeciwdziałający obciążeniu
w kN (zależy od wielkości parametrów geotechnicznych wielkości podstawy fundamentu, sposobu jego obciążenia)

- obliczeniowe obciążenie jednostkowe podłoża pod fundamentem w kN/m^2

- obliczeniowy opór jednostkowy jednowarstwowego podłoża pod fundamentem w kN/m^2

m - współczynnik korekcyjny zależny od metody ustalania parametrów geotechnicznych

W przypadku gdy spełnione są powyższe warunki, wymiary fundamentu określa się przyjmując liniowy rozkład
.

• Obliczenie obciążenia pionowo działającego na fundament osiowo lub na mimośrodzie
  

• Pozioma składowa obciążenia nie przekracza 10% składowej pionowej

• Budowla nie jest usytuowana na zboczu, obok niej nie projektuje się wykopów

(2)

(3)

Wymiary podstawy fundamentu należy tak zaprojektować, aby wypadkowa sił od obliczeniowego obciążenia stałego i zmiennego długotrwałego nie wychodziła poza rdzeń podstawy fundamentu
, a od wszystkich obciążeń obliczeniowych powstała szczelina o zasięgu c (dla fundamentu o podstawie prostokąta i momencie zginającym w jednej płaszczyźnie

Jeżeli fundament jest obciążony siłą pionową i siłą poziomą (równoległą do boku B) to sprawdza się warunek
.We wzorze na
przyjmuje się zredukowaną szerokość podstawy fundamentu

ŁAWY FUNDAMENTOWE: - żelbetowe stosuje się, gdy obliczona wysokość ławy betonowej jest zbyt duża. Jeśli posadowienie na warstwie chudego betonu otulina - 5cm, w przeciwnym razie - 7cm. Obliczenie ławy żelbetowej - określenie jej szerokości, zaprojektowanie zbrojenia na zginanie wsporników ławy oraz ewentualne obliczenie zbrojenia na ścinanie.

Szerokość ławy określa się z warunku
lub
, przyjmując L=1.0m;
;Gdy L>5B to B/L=0

- obliczeniowy ciężar ławy i gruntu spoczywającego na jej odsadzkach w kN.

- wypadkowa siła obliczeniowa przekazywana ze ściany na ławę o dł. L=1.0m, w kN.

Wysokość ław - określa się ekonomicznym stopniem zbrojenia wsporników ławy ( h - zależy od klasy betonu i klasy stali ). Zakłada się wysokość h i oblicza potrzebny przekrój zbrojenia, moment zginający oblicza się dla wspornika o wysięgu d i przekroju Lxh. Obliczone zbrojenie układa się prostopadle do osi podłużnej ławy, stosuje się podłużne pręty i strzemiona jak na rysunku. Ław nie zbroimy na ścinanie, gdy
sprawdzany w przekroju 1-1.

STOPY FUNDAMENTOWE - stosowane, gdy ze względu na kąt rozchodzenia się naprężeń wysokość stopy betonowej była zbyt duża i podstawa stopy betonowej byłaby zbyt mała ze względu na kąt rozchodzenia się naprężeń ściskających.

Stopy obciążone osiowo - podstawa kwadratu,

Stopy obciążone mimośrodowo - niesymetryczne,

Stopy prefabrykowane - kielichowe

Wymiary podstawy stopy B i L określa się metodą kolejnych przybliżeń
. Wysokość stopy żelbetowej przyjmuje się z warunku na przebicie lub zakotwienia prętów pionowych.

Przyjmuje się prostoliniowy rozkład naprężeń jednostkowych w gruncie pod stopą. Stopy wymiaruje się na zginanie oraz główne siły rozciągające, docisk (gdy wytrzymałość betonowej stopy jest mała w porównaniu do wytrzymałości obciążających ją słupów). Najczęściej stosowaną metodą obliczania stóp jest metoda wydzielonych wsporników - podział stopy na cztery niezależne bryły o podstawie trapezu, traktowane jako wsporniki zginane obciążone reakcją gruntu. Zbrojenie oblicza się jak dla elementu zginanego pojedynczo zbrojonego
. W przypadku gdy siła N_rs działa na mimośrodzie e<L/6 obliczamy obciążenie jednostkowe w gruncie pod stopą wg wzorów (2) i (3). Dla ułatwienia wyznaczenia momentów zginających przyjmuje się dla trapezów jako równomiernie rozłożone na całej powierzchni q_ro. W przypadku obciążenia mimośrodowego należy ustalić mimośród
działania siły względem osi słupa, następnie mimośród siły pionowej względem środka postawy stopy e' .

UWAGA: - przy określaniu obliczeniowych obciążeń jednostkowych na podłoże gruntowe przyjmuje się siłę N _r z uwzględnieniem ciężaru fundamentu oraz spoczywającego na nim gruntu. Na określenie warunków wytrzymałościowych nie wpływa ani ciężar fundamentu ani ciężar obciążającego go z góry gruntu, gdyż te składowe obciążenia znoszą się z oddziaływaniem podłoża od tych obciążeń i nie wpływają na odkształcenia obliczanych elementów fundamentu.

Żelbetowe ściany oporowe:

ŚCIANY OPOROWE: - to konstrukcje przeznaczone do powstrzymania parcia gruntu, materiałów sypkich (węgiel, koks itp.). Rozróżniamy ściany: - masywne (betonowe, z kamienia), - lekkie (żelbetowe a tekże częściowo sprężone).

Rodzaje ścian oporowych:

Masywne

W zależności od sposobu zabezpieczenia ścian można je podzielić na:

• ściany oporowe zwykłe, które są w stanie własnym ciężarem zapewnić stateczność

• ściany oporowe z płytami odciążającymi

Płytowo - kątowe

W zależności od sposobu zabezpieczenia stateczności rozróżniamy ściany:

• zwykłe, których stateczność zapewnia płyta fundamentowa

• z elementami odciążającymi, których stateczność zapewnia parcie gruntu działającego na te elementy ( odciągi )

- Ściany z odciągami - odciągi kotwione w gruncie zabezpieczają ścianę przed obrotem i przesuwem.

- Płytowo żebrowe

Określenie obciążeń działających na ściany oporowe

- G_g - od ciężaru gruntu spoczywającego na odsadzkach ściany /iloczyn objętości i ciężaru objętościowego gruntu - wartość charakterystyczna / współczynniki obciążenia dla: gruntów rodzimych
; gruntów nasypowych

- G_b - ciężar własny ściany

- E`_c - parcie naziomu

- E``_c - parcie czynne (poziome) wywołane parciem gruntu /trójkątny wykres/

- E_b - parcie bierne (odpór gruntu)

-
- tarcie między podeszwą fundamentu i gruntem

-
- parcie odporem gruntu na płytę fundamentową ściany oporowej

Parcie poziome:

STATYKA ŚCIAN OPOROWYCH:

Obliczenia sprawdzające ogólną stateczność ścian oporowych należy wykonywać przy założeniu walcowych powierzchni poślizgu stosując metodę Felleniusa lub Bishopa.

Obliczenia dotyczą:

1. Stateczności na obrót względem najbardziej obciążonej krawędzi podstawy fundamentu.

2. Stateczność na przesunięcie ze ścięciem poziomym lub ukośnym.

Ad.(a). Uproszczone sprawdzenie stateczności ściany oporowej na obrót względem krawędzi podstawy fundamentu polega na sprawdzeniu warunku:

M_or - moment wszystkich sił obliczeniowych powodujących obrót ściany (moment wywracający)

M_ur - moment wszystkich sił obliczeniowych przeciwdziałających obrotowi ściany (moment utrzymujący)

m_o - zależnie o obciążenia naziomem: gdy
, w pozostałych przypadkach m_o=0.9

Ad.(b). Uproszczone sprawdzenie stateczności ściany oporowej na przesunięcie przeprowadza się gdy obliczeniowy kąt nachylenia (w stosunku do pionu) wypadkowej obciążenia działającego w podstawie fundamentu ściany jest większy niż obliczeniowy kąt tarcia wewnętrznego
gruntu obciążającego ścianę.

W tym przypadku należy sprawdzić:

Q_tr - obliczeniowa wartość składowej stycznej (poziomej) obciążenia w płaszczyźnie ścięcia.

Q_tf - suma rzutów na płaszczyznę ścięcia wszystkich sił obliczeniowych przeciwdziałających przesunięciu ściany.

m_t - zależnie o obciążenia naziomem: gdy
, w pozostałych przypadkach m_t=0.9

Tarcie T = p * f

f - współczynnik tarcia pomiędzy podeszwą fundamentu a gruntem, zależy od rodzaju i wilgotności gruntu

(w Polsce około 0.55-0.10)

p - pionowa składowa obliczeniowego obciążenia podłoża

Zasady zbrojenia.

Ściany żelbetowe kątowe do

Zwykłe kątowe nie przekraczają 1.5m (w rowach odwadniających)

Gr. pionowej płyty w najcieńszym miejscu 10cm, a w miejscu połączenia płyty pionowej z płytą fundamentową około 15cm (1/12 - 1/15h)

Gr. płyty poziomej min.15cm i nie mniej niż grubość płyty pionowej u nasady

Należy stosować skosy. Szerokość podstawy ½ - 3/5h

Ściany kątowe z wysuniętą odsadzką 0.2-0.3 długości płyty fundamentowej.

Ściany płytowo żebrowe:

Rozstaw żeber - 3.5-5.0m

Minimalna szerokość żeber - 25cm

Grubość płyty pionowej - 1/9 - 1/15 odstępu żeber

Grubość płyty fundamentowej - przynajmniej grubość płyty pionowej przy fundamencie (1/10-1/15h), na końcach wsporników 1/15-1/20h_pł.

Jeżeli rozstaw żeber jest nie większy od dwukrotnej ich wysokości to płytę pionową można obliczać jako dwukierunkowo zbrojoną (utwierdzoną na trzech krawędziach)

Jeśli płytę liczymy jako ciągłą:

• dla każdej strefy z wyjątkiem najniżej przylegającej do płyty fundamentu przyjmujemy obciążenie równe rzeczywistemu obciążeniu w środku wysokości strefy

• dla pasma dolnego - obciążenie zredukowane do połowy wartości średniego działającego tu pasma.

Płytę pionową zbroi się jako ciągłą natomiast w pasie dolnym dodatkowe zbrojenie pionowe potrzebne do przeniesienia momentów utwierdzenia w płycie fundamentowej. W przybliżeniu można przyjąć że obciążenie parciem gruntu działające na części płyty wydzielonej dwusiecznymi kątów naroży wywołuje moment utwierdzenia.

Żebra - projektujemy jako wsporniki o przekroju T i zmiennej wysokości

Obliczone zbrojenie umieszcza się w tylnej powierzchni żeber kotwiąc je w płycie dolnej. Płytę pionową należy kotwić w żebrach za pomocą strzemion zamkniętych obejmujących cały przekrój żebra.

Strzemiona należy tak zaprojektować, aby można było przenieść z płyty na żebra całkowitą siłę odrywającą wywołaną parciem gruntu.

22.Ogólne

Zasady projektowania i kształtowania zbrojenia w prostych elementach konstrukcyjnych:

PŁYTY

• Średnica prętów stosowanych do zbrojenia płyt powinna być nie mniejsza niż 4,5 mm. W przypadku siatek zgrzewanych dopuszcza się stosowanie drutów o średnicy 3 mm.

• Do podpory należy doprowadzić bez odgięć nie mniej niż 1/3 dolnych prętów potrzebnych w przęśle i nie mniej niż 3 pręty na 1 m szerokości przekroju.

• Jeżeli na podporze nie występują warunki zapewniające swobodę obrotu, należy stosować odpowiednie zbrojenie górne.

• Pręty rozdzielcze powinny mieć rozstaw nie większy niż 300 mm oraz łączną nośność nie mniejszą niż :

• 1/10 nośności zbrojenia głównego przy obciążeniu równomiernie rozłożonym

• ¼ nośności zbrojenia głównego przy obciążeniu równomiernie rozłożonym i obciążeniu siłami skupionymi w przypadku, gdy momenty zginające wywołane obciążeniami skupionymi są nie większe niż 50% momentów całkowitych. W przeciwnym przypadku zbrojenie prostopadłe dozbrojenia głównego należy odpowiednio obliczyć.

• W przypadku otworów występujących w polu płyty, obrzeża otworów powinny być dodatkowo zbrojone. Jeżeli wymiary otworu nie przekraczają 1/4 obliczeniowej rozpiętości płyty, zaś obliczeniowe obciążenie płyty ponad ciężar własny nie większe niż 10 kN/m², przekrój zbrojenia obrzeżnego powinien być nie mniejszy niż przekrój zbrojenia przypadającego na szerokość otworu. W przeciwnym przypadku wzmocnienie płyty przy otworze należy zaprojektować w postaci wymianów. Przy przyjęciu wymianów jako belek ukrytych w grubości płyty, ich szerokość nie może przekraczać 4 grubości płyty.

• W płycie ze zbrojeniem głównym ułożonym równolegle do podpory, którą stanowi belka lub ściana, należy zastosować dodatkowe zbrojenie górne, prostopadłe do tej podpory, o nośności nie mniejszej niż 1/3 nośności zbrojenia głównego w tej płycie, o przekroju zdolnym przenieść siłę rozciągającą nie mniejszą niż 40 kN/m długości podciągu. Zbrojenie to powinno być wpuszczone w płytę na długość nie mniejszą niż 1/4 obliczeniowej rozpiętości płyty po każdej stronie podpory, licząc od jej krawędzi. Jednocześnie zbrojenie główne płyty w paśmie o szerokości równej 1/4 obliczeniowej rozpiętości płyty, przylegającym do tej podpory, można zredukować do połowy.

Zbrojenie płyt dwukierunkowo zbrojonych należy konstruować zgodnie z założeniami metody obliczania momentów zginających.

W jednoprzęsłowych płytach podpartych na 4 krawędziach, obliczanych wg analizy liniowo sprężystej zbrojenie powinno przebiegać następująco:

• Zbrojenie każdego z dwóch kierunków wyznaczone dla środkowej części płyty powinno być układane w paśmie środkowym o szerokości równej 3/5 szerokości płyty.

• W pasmach skrajnych, obejmujących po 1/5 szerokości płyty, przekrój zbrojenia może być zmniejszony do połowy.

• W narożach wolno podpartych należy umieszczać dwukierunkowe zbrojenie górne, równoległe do krawędzi, na szerokości równej 0,3 mniejszej rozpiętości. Przekrój tego zbrojenia na jednostkę szerokości przekroju płyty powinien wynosić w każdym kierunku co najmniej połowę przekroju większego zbrojenia znajdującego się w

• środku płyty.

Rys. Połączenie płyty z podciągiem

• W narożach, w których zbiega się krawędź swobodnie podparta z krawędzią zamocowaną, postanowienie to rozciąga się jedynie na zbrojenie naroża równoległe do krawędzi zamocowane, natomiast przekrój zbrojenia prostopadłego do krawędzi zamocowanej wynika z obliczeń.

• W narożach wolno podpartych należy również umieszczać dodatkowe zbrojenie dolne, układane prostopadle do dwusiecznej i rozmieszczone na szerokości równej 0,2 mniejszej rozpiętości płyty. Przekrój tego zbrojenia na 1 m szerokości przekroju powinien być co najmniej równy przekrojowi większego zbrojenia w środku płyty.

Rys. Zbrojenie płyt krzyżowo zbrojonych :

1 - zbrojenie dolne,

2 - zbrojenie górne

BELKI

Średnica podłużnych prętów rozciąganych nie powinna być mniejsza niż :

• 8 mm - w belkach wykonanych na miejscu budowy

• 5,5 mm - w belkach prefabrykowanych

Średnica podłużnych prętów ściskanych nie powinna być mniejsza niż :

• 12 mm - w belkach wykonanych na miejscu budowy

• 10 mm - w belkach prefabrykowanych

W belkach żelbetowych co najmniej 1/3 prętów zbrojenia dolnego potrzebnych w przęśle i nie mniej niż dwa pręty powinny być doprowadzone bez odgięć do podpory.

Średnica strzemion powinna być nie mniejsza niż :

• 4,5 mm - w belkach wykonanych na miejscu budowy

• 3,0 mm - w belkach prefabrykowanych

Ponadto średnica strzemion powinna być nie mniejsza niż 0,2 średnicy zbrojenia podłużnego.

Średnica strzemion wykonanych z prętów gładkich nie powinna być większa niż 12 mm.

Pręty powinny być odpowiednio zakotwione. Połączenie na zakład przy powierzchni bocznej środnika dopuszcza się tylko dla prętów żebrowanych.

Stopień zbrojenia na ścinanie nie może być mniejszy od wartości podanych w tabeli (w zależności od klasy stali i klasy wytrzymałości betonu).

Maksymalny odstęp ramion strzemion s_max w kierunku podłużnym określają warunki :

• dla
  s_max = 0,8d ≤ 300 mm

• dla
  s_max = 0,6d ≤ 300 mm (*)

• dla
  s_max = 0,3d ≤ 200 mm (**)

Maksymalny odstęp strzemion s_max w kierunku poprzecznym nie powinien przekraczać :

• przy
  mniejszej z dwóch wartości : s_max = d lub800 mm

• przy
  obowiązują warunki (*) i (**)

Rys. Rozstaw prętów odgiętych w strefie przypodporowej

Pręty odgięte uwzględnione w obliczeniach, powinny być rozmieszczane w strefie przypodporowej tak, aby odległości s_a i s_b były nie większe od wartości podanych na rysunku :

Jeżeli w belce zastosowano pręty ściskane, potrzebne ze względów obliczeniowych, rozstaw strzemion zamkniętych nie powinien być większy niż 15 średnic tego zbrojenia.

W belkach prostokątnych nie połączonych z płytami, należy stosować strzemiona zamknięte. W belkach o szerokości większej niż 350 mm zbrojonych w strefie rozciąganej więcej niż 3 prętami, należy stosować strzemiona czteroramienne.

Zbrojenie elementów skręcanych lub jednocześnie skręcanych i zginanych powinno składać się z dwuramiennych strzemion i dodatkowych - w stosunku do zbrojenia ze względu na moment zginający - prętów podłużnych rozmieszczonych równomiernie na obwodzie rdzenia belki. Zbrojenie elementów skręcanych, jeżeli znak momentu skręcającego nie ulega zmianie, można projektować w postaci uzwojenia o kierunku zgodnym z kierunkiem skręcania. Rozstaw prętów uzwojenia powinien być nie większy niż mniejszy bok przekroju prostokątnego.

W elementach skręcanych należy stosować strzemiona zamknięte, łączone na zakład o długości równej co najmniej 30 średnic strzemienia, lub łączone za pomocą spajania.

Odstęp strzemion powinien spełniać warunki jak dla elementów zginanych.

RAMY

Węzły, załamania oraz naroża ram należy tak konstruować, aby pręty zbrojeniowe rozciąganej strefy nie miały tendencji do wyrwania się przy ich prostowaniu się na wskutek przenoszenia naprężeń rozciągających.

Zbrojenie elementów o kształcie załamanym :

• Belki o kształcie załamanym, w których pręty rozciągane znajdują się od strony wklęsłej, należy zbroić przez skrzyżowanie tych prętów w punkcie załamania belki. Należy przyjmować dla prętów odpowiednią długość zakotwienia od miejsca skrzyżowania.

Rys. Zbrojenie elementów załamanych przy α ≥ 15°

• W przypadku, gdy kąt załamania elementu jest mniejszy niż 15°, zbrojenie rozciągane można załamać, pod warunkiem zabezpieczenia prętów przed wyrwaniem za pomocą dodatkowych strzemion. Strzemiona te powinny odpowiadać następującym warunkom :

• sumaryczne pole przekroju strzemion powinno wynosić :

, gdzie :

A_S - pole przekroju prętów załamanych

α - kąt załamania elementu,

• każdy załamany pręt rozciągany musi być uchwycony co najmniej przez jedno ramię strzemion

• przy średnicy prętów załamanych większej niż 20 mm pręty i strzemiona powinny być ze sobą zespawane

Rys. Zbrojenie elementów załamanych przy α < 15°

• strzemiona, których przekrój obliczony jest wg powyższego wzoru, powinny być rozstawione na długości nie większej niż 8 średnic prętów załamanych, licząc w każdą stronę od miejsca załamania

W elementach zakrzywionych każdy zakrzywiony pręt rozciągany o średnicy większej niż 12 mm, znajdujący się po wklęsłej stronie elementu, powinien być uchwycony co najmniej przez jedno ramię strzemienia. Odstęp strzemion nie powinien w tym przypadku przekraczać 1/4 promienia krzywizny.

Prawidłowe rozwiązanie węzła sztywnego monolitycznego - zbrojenie rygla przedłużeniem zbrojenia słupa.

Rys. Błędne (a) i prawidłowe (b) skonstruowanie sztywnego monolitycznego węzła

Przy konstruowaniu zbrojenia w skosie słupa należy rozróżnić dwie odmiany skosów :

• krótki skos - pręty dolne wpuszcza się w słup, skos zbroi się konstrukcyjnie

2. 
   

Rys. Konstrukcja węzła monolitycznego sztywnego

1. przy skosie konstrukcyjnym

2. przy skosie mającym znaczenie konstrukcyjno-wytrzymałościowe

• długie skosy - mające na celu zwiększenie wysokości rygla w przekroju przypodporowym, w którym występują znaczne momenty ujemne, lub też zmniejszenie naprężeń ścinających w tym przekroju. Przy długich skosach zbrojenie rygla może być łączone (na zakład) na początku skosu, ale wzdłuż jego pochylenia należy wówczas umieścić zbrojenie z co najmniej dwóch prętów o łącznym przekroju równym co najmniej 1/3 przekroju zbrojenia przęsłowego. Długość zakładu l_a ≥ 30d.

Dolne pręty zbrojenia rygla wpuszcza się w słup na długość równą co najmniej 15d.

Górne pręty zbrojenia przypodporowego wpuszcza się w skrajny słup tak, aby zapewnić im należytą przyczepność. W tym celu należy e przedłużyć co najmniej o 30d poniżej dolnej linii rygla.

Szczególną uwagę należy zwrócić na konstruowanie naroży ustrojów ramowych. Z doświadczeń wynika, że największe rozciąganie nie występuje w punkcie narożnym, lecz przesuwa się do osi geometrycznej ramy. Z tego względu właściwiej jest stosować wkładki zewnętrzne zaokrąglone o promieniu r > 20 średnic głównego zbrojenia. Podział naprężeń w węźle zależy również od wielkości kąta wewnętrznego jaki tworzy połączenie dwóch prętów narożnych. Przy kącie prostym występują największe ściskające naprężenia normalne prostopadle skierowane do siecznej kąta, zatem im łagodniej jest skonstruowane przejście słupa w rozporę, tym mniejsze są naprężenia miejscowe w węźle. W związku z tym w ustrojach ramowych stosuje się w węzłach skosy lub przejścia zaokrąglone.

Rys. Konstruowanie połączenia rygla ze słupem w ramie monolitycznej a) wpływ kształtu naroża ramy na przebieg naprężeń wewnętrznych b) konstrukcje połączeń

21. Ogólne

Projektowanie przekroju żelbetowego/sprężonego w elementach konstrukcyjnych w rożnych stanach obciążenia:

PROJEKTOWANIE I SPRAWDZANIE NOŚNOŚCI PRZEKROJÓW PROSTOKĄTNYCH I TEOWYCH

Wstęp

Modele analityczne konstrukcji

Analizowana konstrukcja składa się zwykle z różnego rodzaju elementów konstrukcyjnych spełniających różne funkcje, np. z belek, słupów, płyt, ścian, tarcz, luków itp.

Klasyfikacji elementów do określonej grupy dokonuje się na podstawie następujących zasad:

- za belkę lub słup uważa się element, którego rozpiętość lub długość jest nie mniejsza niż dwukrotna wysokość przekroju. Belkę, której rozpiętość jest mniejsza niż dwukrotna wysokość przekroju, nazywamy belką-ścianą,

- za płytę uważa się element konstrukcyjny, którego mniejsza z rozpięto­ści jest większa od czterokrotnej grubości elementu,

• za ścianę uważa się element pionowy, którego długość w kierunku poziomym jest większa niż czterokrotna jego grubość.

Płytę można uważać za element jednokierunkowo rozpięty jeżeli:

— dwie jego krawędzie w przybliżeniu równolegle są nie podparte, lub

— stanowi część środkową płyty w przybliżeniu prostokątnej, podpartej na czterech krawędziach, o stosunku boków większym od 2.

• Dane geometryczne

l) Obliczeniowa rozpiętość belek

Obliczeniową rozpiętość elementu l_eff wyznaczać można ze wzoru:

l_eff = l_n +a₁ + a₂

gdzie:

l_n — rozpiętość elementu w świetle podpór,

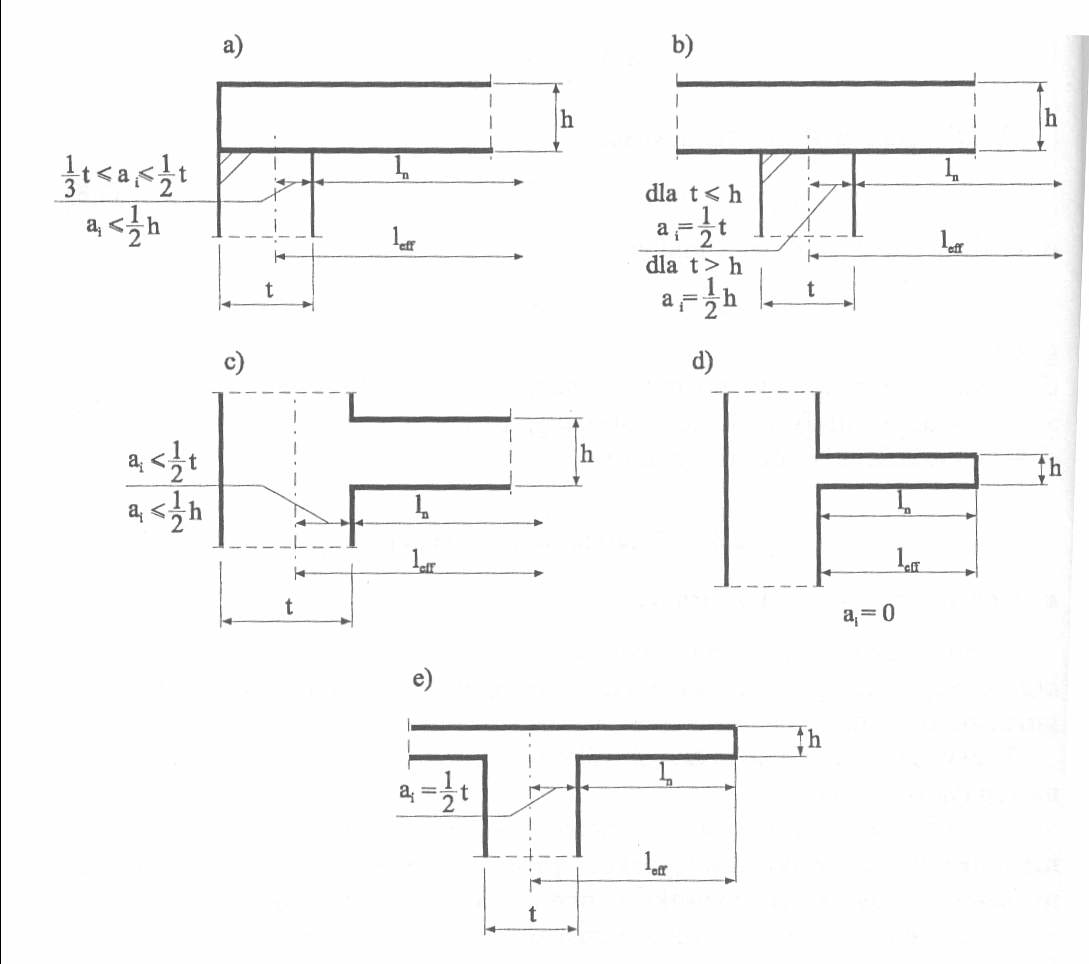
a₁ i a₂ — odległość teoretycznych punktów podparcia elementu od krawędzi podpór według rys. 2.1.

Ogólne zasady obliczania elementów zginanych, ściskanych i rozciąganych

Sprawdzenia stanu granicznego nośności elementów zginanych, ściskanych i rozciąganych dokonuje się przyjmując następujące założenia:

— przekroje płaskie przed odkształceniem pozostają płaskimi również po odkształceniu,

— przy ustalaniu warunków równowagi sił wewnętrznych w przekroju pomija się wytrzymałość betonu na rozciąganie,

— naprężenia w betonie ściskanym i w stali ustala się zgodnie z wykresami zamieszczonymi na rys. 1.1 lub alternatywnie wykres prostokątny oraz na rys. 1.5 lub alternatywnie wykres z półką poziomą (dla stali),

— rozkład odkształceń w przekroju przyjmuje się według rys. 2.4,

— stan graniczny nośności występuje wówczas, gdy osiągnięty jest przynaj­mniej jeden z następujących warunków:

a) w zbrojeniu rozciąganym _s = —0,01,

b) w skrajnym włóknie betonu _c = 0,0035

c) we włóknie betonu położonym w odległości 3/7 h od

bardziej ściskanej krawędzi przekroju _c = 0,002.

Rys. 2.4.Wykres odkształceń przekrojów w stanie granicznym nośności elementu pojedynczo zbrojonego:

Siłę podłużną działającą w przekroju zginanym można pominąć, jeżeli średnie naprężenie ściskające wywołane przez tę siłę nie przekracza 0,08 f_ck ( wtedy    .

Ogólne zasady sprawdzania stanu granicznego nośności ugięciowej:

Sprawdzenie stanu granicznego nośności ugięciowej polega na wykazaniu, że w każdym przekroju belki lub płyty zginanej, moment zginający wywołany działaniem obciążeń obliczeniowych (lub innymi oddziaływaniami) jest mniej­szy lub równy maksymalnemu momentowi wywołanemu działaniem sił we­wnętrznych, tzn. M_sd < M_Rd. Powstające w elemencie siły wewnętrzne do­prowadzają do powstania stanu granicznego nośności, gdy

a) odkształcenie w stali rozciąganej osiągnie _s = 10 %o.

b) odkształcenie w skrajnym ściskanym włóknie betonu będzie równe _c = 3.5 %o

W celu wyznaczenia sil wewnętrznych przyjmuje się następujące założenia:

a) obowiązuje prawo płaskich przekrojów,

b) wytrzymałość betonu na rozciąganie jest pomijana,

c) naprężenia w ściskanej strefie betonu mają przebieg paraboliczno-prostokątny lub alternatywnie prostokątny,

d) stal zbrojeniową traktuje się jako materiał sprężyste — idealnie plas­tyczny lub alternatywnie plastyczny ze wzmocnieniem.

Ze względu na możliwość zastosowania alternatywnych kształtów brył naprężeń w strefie ściskanej betonu (punkt c), wprowadza się pojęcie dwóch dopuszczalnych modeli obliczeniowych.

W pierwszym modelu zależność pomiędzy odkształceniami i naprężeniami ma postać (σ_c = _c (l — 0.25 _c ) α*f_cd gdzie α = 0,85, _c w promilach. Przy stosowa­niu tego modelu trzeba uwzględnić wszystkie podane powyżej założenia dotyczące warunków granicznych odkształceń betonu i stali oraz prawo płaskich przekrojów.

Drugi model jest uproszczony. Obliczenia przeprowadza się przy założeniu,

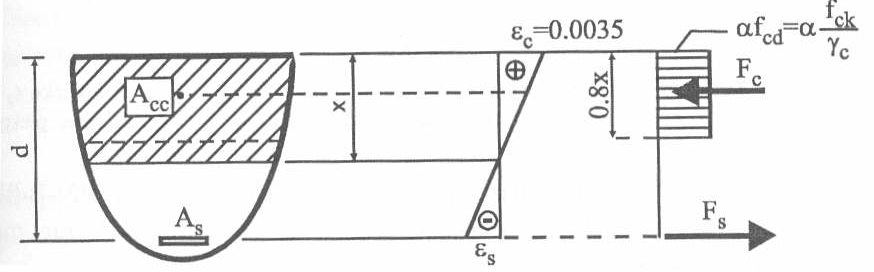
Wymiarowanie przekrojów zginanych przy założeniu prostokątnego kształtu bryły naprężeń

Przy sprawdzaniu nośności i wymiarowaniu bierze się pod uwagę tzw. efektywną wysokość strefy ściskanej x_eff = 0,8x.

W celu zapewnienia odpowiedniego wykorzystania stali w strefie rozciąganej wprowadzone jest ograniczenie względnej wysokości strefy ściskanej

ξ_eff = x_eff /

Wymiarowanie przekrojów prostokątnych pojedynczo zbrojonych (również II.24.)

αf_cd

αf_cdbx_eff

x_eff

d M_sd

h

A_s1 AA A_s1f_yd

b

Układ sił w zginanym przekroju pojedynczo zbrojonym

Przy wymiarowaniu niewiadomymi są: efektywna wysokość strefy ściskanej x_eff oraz powierzchnia zbrojenia A_s1. Wielkości te można wyliczyć korzystając z równań równowagi. Warunek równowagi momentów obliczonych względem środka ciężkości zbrojenia ma postać:

M_sd ≤ M_Rd = αf_cd • b • x_eff (d - 0,5 x_eff).

Jest to równanie kwadratowe, z którego wylicza się x_eff mianowicie :

s_c = M_sd /(b d² α f_cd ) ξ_eff = 1-√(1-2 s_c ) ≤ ξ_eff,lim x_eff = ξ_eff /d

Równanie równowagi sił pozwala natomiast wyliczyć pole powierzchni stali A_s1.

A_s1 f_yd = αf_cd • b • x_eff

mianowicie : A_s1 = αf_cd • b • x_eff / f_yd ≥ A_smin

Minimalne pole zbrojenia określamy wg. p.4.8 s.42 PN i p.6.2 s.78 (ze względu na skurcz )

Z zależności tych można korzystać, gdy obliczona wysokość efektywnej strefy ściskanej nie jest zbyt duża.

Górne ograniczenie x_eff wynika z warunku wykorzystania naprężeń w stali, tzn. ε_s ≥ ε_pl = f_yd / E_s

Po wykorzystaniu prawa płaskich przekrojów względną wysokość tej strefy ξ_eff,lim= x_eff,lim / d można odczytać z tabeli .

Tabela 3.5. Maksymalne wartości względnej wysokości strefy ściskanej betonu

Stal	A-0	A-I	A-II	A-III	A-IIIN
ξeff,lim	0,63	0,62	0,55	0,53	0,50

Jeżeli ξ_eff okaże się większe od wartości podanych w tabeli, to oznacza że nośności strefy ściskanej przekroju jest zbyt mała. Należy więc albo zwiększyć wymiary przekroju, albo zastosować zbrojenie w strefie ściskanej.

Przekroje prostokątne podwójnie zbrojone (również II.24.)

Z takimi przypadkami mamy do czynienia, gdy przy wymiarowaniu przekroju pojedynczo zbrojonego otrzymuje się ξ_eff >ξ_eff,lim lub gdy zbroje­nie w strefie ściskanej znajduje się tam ze względów konstrukcyjnych.

W pierwszym przypadku przy wymiarowaniu występują trzy niewiadome A_s1, A_s2 i x_eff, a do dyspozycji są tylko dwa liniowo niezależne równania równowagi. Trzecie równanie można sformułować korzystając z warunku minimalnego zużycia stali zakładając :

ξ_eff = ξ_eff,lim

pozostałe niewiadome obliczamy z równań

M_sd = αf_cd • b • x_eff (d - 0,5 x_eff)+ A_s2 f_yd ( d- a₂ ) oraz (1)

A_s1 f_yd = αf_cd • b • x_eff + A_s2 f_yd (2)

tzn. przy założeniu x_eff = ξ_eff,lim /d liczymy A_s2 z równania

A_s2 =( M_sd - αf_cd • b • x_eff (d - 0,5 x_eff)) / f_yd ( d- a₂ )

Następnie z równania (2) liczę A_s1

Jeżeli zbrojenie w strefie ściskanej jest zadane konstrukcyjnie, to niewiado­mymi są A_s1 , x_eff związku z tym nie ma potrzeby formułowania dodatkowych warunków, a wartość Xeff wylicza się z równania (1). Konieczne jest jednak sprawdzenie, czy

0,5 x_eff ≥ a₂

Gdy warunek jest spełniony, to powierzchnię zbrojenia rozciąganego wylicza się ze wzoru (2). Przeciwny przypadek oznacza, że ilość stali w strefie ściskanej jest zbyt duża i jest ono wykorzystane jedynie częściowo Wtedy powierzchnię zbrojenia wylicza się z równania:

M_sd = A_s1 f_yd (d-a₂) (3)

Wymiarowanie przekrojów teowych

Określanie szerokości płyty współpracującej

Współpracę płyty uwzględniamy gdy :

• Grubość płyty jest nie mniejsza niż 0.05h oraz nie mniejsza niż 3cm

• Płyta jest monolitycznie połączona z belką

• W płycie znajduje się odpowiednie zbrojenie ułożone prostopadle do belki

Jako b_eff należy przyjąć najmniejszą z wartości :

• dla przekrojów symetrycznych

b_w +l_o /5

b_eff = min 12 h_f +b_w ≤ b

• dla przekrojów z półką z 1 strony

b_w +l_o /10

b_eff = min 4 h_f +b_w ≤ b

Dla belek obciążonych siłą skupioną , której wartość jest większa od pozostałego łącznego obciążenia belki , szerokość wysięgu płyty należy zmniejszyć o 20%

Wymiarowanie przekrojów pozornie teowych

Jeżeli do wymiarowania zakłada się prostokątny wykres naprężeń w strefie ściskanej betonu, to celowe jest wyodrębnienie dwóch przypadków zależnych od położenia osi obojętnej. Gdy oś obojętna znajduje się w pólce, to przekrój taki nazywamy pozornie teowym. Ponieważ w metodzie stanów granicznych pomija się pracę betonu w strefie rozciąganej, to w tym wypadku przekrój wymiaruje się jak przekrój prostokątny o szerokości b_eff i wysokości użyt­kowej d. Przekrój nazywamy rzeczywiście teowym, gdy oś obojętna przechodzi przez środnik .

W celu sprawdzenia, z którym przypadkiem mamy do czynienia, rozpat­rujemy przypadek graniczny zgodnie z rysunkiem

Schemat obliczeniowy służący sprawdzeniu typu przekroju teowego

Moment „przenoszony" przez taki przekrój można wyliczyć jako sumę momentów względem środka ciężkości zbrojenia rozciąganego:

M= αf_cd • b_eff • h_f (d - 0,5 h_f)

Jeżeli M_sd > M, to przekrój jest rzeczywiście teowy, a w przypadku gdy M_sd ≤ M przekrój jest pozornie teowy.

Równania równowagi dla przekroju (a) :

M₁ = αf_cd • (b_eff - b_w) • 0.8h_f (d - 0,5 h_f)

A_s1,1 f_yd = αf_cd • (b_eff - b_w) • 0.8h_f

Równania równowagi dla przekroju (b) :

M₂=M_sd - M₁ = αf_cd • b_w • x_eff (d - 0,5 • x_eff )

A_s1,2 f_yd = αf_cd • b_w • x_eff

x_eff wylicza się ze wzoru na M₂ a ostateczna powierzchnia zbrojenia A_s1 = A_s1,1 + A_s1,2

Wymiarując te przekroje należy również pamiętać o granicznej wartości strefy ściskanej

OBLICZANIE ZBROJENIA NA ŚCINANIE

O ile w środku rozpiętości belki naprężenia główne mają kierunki zgodne z osiami belki, to przy podporach kierunki te są nachylone do osi. Konsekwen­cją tego jest (po odpowiednim wzroście obciążenia) powstanie rys prostopad­łych do osi belki w środku jej rozpiętości oraz rys ukośnych w okolicach podpory.

Do chwili powstania rys ukośnych naprężenia wywołane ścinaniem przeno­szone są przez beton oraz przez zbrojenie podłużne. Występowanie znacznych sił tnących pogarsza warunki współpracy stali i betonu i powoduje konieczność staranniejszego kotwienia tych prętów na podporze.

Po powstaniu rys ukośnych w belce schemat pracy i trajektorie naprężeń ulegają zmianie. W klasycznych modelach zakłada się, że główną rolę za­czynają odgrywać strzemiona, pręty odgięte oraz beton ściskany. Pomija się natomiast wpływ betonu w strefie rozciąganej pomiędzy rysami oraz odkształ­ceń poprzecznych zbrojenia. Istotę klasycznego modelu reprezentuje klasyczna analogia kratownicowa .

W najprostszym przypadku, jeżeli zbrojenie belki składa się wyłącznie ze zbrojenia głównego i strzemion, analogia kratownicowa pokazana jest na rysunku

s - rozstaw strzemion

F_cwd F_swd

z=0,9 d

 

c=z*cot 

F_cwd V_Rd2



V_sd<F_swd F_swd=f_ywd*c*A_sw/s

V_sd<V_Rd2 V_Rd2=F_cwd*sin  V_Rd2=*f_cd*b_w*z*1/(cot tg 

F_cwd = σ_c*c* sin b_w σ_c<*f_cd

Pas górny kratownicy tworzy beton strefy ściskanej, a pasem dolnym jest rozciągane zbrojenie główne. Ukośne krzyżulce (linia przerywana) to beton, który jest ściskany, a pionowe słupki to rozciągane strzemiona. Analogicznie wyglądałaby sytuacja, gdyby zamiast pionowych strzemion przyjąć krzyżulce ukośne reprezentujące pręty odgięte. Przy takich schematach można jedno­znacznie wyznaczyć siły w betonie i zbrojeniu. Jeżeli powierzchnię strzemion (przy przyjęciu odpowiednich naprężeń dopuszczalnych dla stali) obliczy się zakładając, że przeniosą one całą siłę Q, to taki element nazywa się w pełni zabezpieczonym przed ścinaniem.

s - rozstaw prętów

F_swd F_cwd

α θ

z cotθ z cotα

F_cwd V_Rd2



V_sd<F_swd F_swd=f_ywd*c*A_sw/s

V_sd<V_Rd2 V_Rd2=F_cwd*sin 

F_cwd=σ_c*c* sin b_w σ_c<*f_cd

V_Rd2=*f_cd*b_w*z*1/(cot tg 

V_Rd3 F_swd

α

c=z (cotθ + cotα)

V_sd ≤ F_swd F_swd = f_ywd*c*A_sw / s

V_sd ≤V_Rd3

F_swd =σ_s*c* A_sw /s σ_s ≤ f_ywd

V_Rd2=*f_cd*b_w*z*( cotθ + cotα))/(1+cot² 

V_Rd3= z* f_ywd ( cotθ + cotα)*sinα *A_sw / s

Sytuacja komplikuje się, gdybyśmy w analo­giczny sposób chcieli określić optymalny układ sił przy jednoczesnym uwzględ­nieniu betonu, strzemion i prętów odgiętych.

W tym przypadku kratownica staje się statycznie niewyznaczalna i stopień wykorzystania któregoś z elementów należy założyć. Trzeba jednak pamiętać że min. 50% siły muszą przenieść strzemiona .

W obecnie wprowadzanej normie zmodyfikowana metoda kratownicowa stanowi podstawę wymiarowania przekrojów na ścinanie.

Sprawdzanie nośności przekrojów ukośnych — odcinki pierwszego rodzaju

Przy sprawdzaniu nośności przekrojów rozróżnia się dwa podstawom przypadki. Pierwszy dotyczy sytuacji, gdy dodatkowe zbrojenie na ścinanie m jest konieczne. Ma to miejsce wtedy, gdy w schemacie kratownicowym można przyjąć, że krzyżulce rozciągane są utworzone z betonu.

Odpowiada to sytuacji, gdy beton przenosi naprężenia rozciągając a zbrojenie rozciągane jest tak zakotwione, że przyrost siły w nim nie powoduje naruszenia przyczepności. W przypadku typowych belek zginanych belka nie wymaga sprawdzenia na ścinanie, gdy spełniony jest warunek:

V_sd ≤ V_Rd1 = (1.4*k τ_Rd (1.2+40ρ_l)+0.15σ_cp)*b_w d

Występująca we wzorze wielkość τ_Rd jest wytrzymałością betonu na| ścinanie i wynosi τ_Rd = f_ctd• 0,25. Naprężenie σ_cp jest naprężeniem normalnym, które jest wywołane obciążeniem lub sprężeniem. W typowych elementach zginanych σ_cp = 0. Wpływ zbrojenia podłużnego jest uwzględniony za pomocą stopnia zbrojenia ρ_l. Przy jego obliczaniu nie można uwzględnić prętów, które kończą się w odległości mniejszej niż długość zakotwienia od końca analizowanego przekroju ukośnego. Należy przy tym przyjmować ρ_l < 0,02. Szerokość b_w określa najmniejszą szerokość analizowanego przekroju (np. dla teowników — środnik). Współczynnik k określający efekt skali jest równy:

k = 1.0 jeżeli do podpory doprowadzono mniej niż 50% prętów,

l,6-d [d]=m. |

W większości typowych przypadków warunek na V_Rd1 jest wystarczający, ale zgodnie z normą należy obliczyć jeszcze V_Rd2 i jako miarodajną przyjąć mniejszą z tych dwóch wartości

V_Rd2 =0.5*f_cd*b_w*z

Równanie to określa nośność ściskanych krzyżulców. Warunek ten nabiera znaczenia, gdy belka jest obciążona znaczną silą normalną. Wtedy należy obliczyć

V_{Rd2 ,red}=1.67 V_Rd2 (1- σ_cp /f_cd ) ≤ V_Rd2

Współczynnik efektywności v dany jest wzorem:

  f_ck /200 ≥ 0.4

zbrojenie samymi strzemionami pionowymi

Taki typ zbrojenia stosuje się, gdy siła tnąca nie jest zbyt duża (długość odcinka drugiego rodzaju nie przekracza 2—3d) lub kiedy odginanie prętów zbrojenia głównego jest utrudnione lub wręcz niemożliwe.

Siła w rozciąganym krzyżulcu jest równa

V_Rd3 =A_sw1 * f_ywd1 *z *cotθ /s₁

Maksymalna silą w ściskanym krzyżulcu betonowym jest wyrażona wzorem:

V_Rd2 = *f_cd*b_w*z*cos   sin 

zbrojenie strzemionami i prętami odgiętymi

W przypadku zastosowania takiego zbrojenia maksymalna siła w krzyżulcu rozciąganym (składowa pionowa) jest równa:

V_Rd3 = A_sw1 * f_ywd1 *z *cotθ /s₁ + A_sw2 * f_ywd2 *z *( cotθ + cotα)*sinα /s₂

Wzór ten oznacza, że siły w krzyżulcu rozciąganym ulegają sumowaniu . Siłę w krzyżulcu betonowym oblicza się ze wzoru

V_Rd2 = *f_cd*b_w*z*( cotθ + cotα))/(1+cot²  - A_sw1 * f_ywd1 *z *cotα /s₁

Jeżeli założy się, że beton w strefie rozciąganej uległ zarysowaniu i nie przenosi naprężeń, to jego rolę musi odegrać zbrojenie.

Jeżeli zbrojenie strefy podporowej składa się tylko ze strzemion, to warunki równowagi prowadzą do zależności

ΔF₁ =V_sd cotθ, a jeżeli są dodatkowo pręty odgięte, to one przenoszą część siły poziomej i wtedy

ΔF₁ =V_sd cotθ - V_sd cotα

Ponieważ około połowy tej siły przenosi beton w pasie górnym, to ostatecznie po uwzględnieniu zginania otrzymuje się:

T_d = M_sd /z + 0.5 ΔF₁

Siła w zbrojeniu T_d musi być mniejsza niż A_s1*f_yd . Warunek ten nabiera istotniejszego znaczenia przy podporach belek ciągłych lub w belkach wspor­nikowych, gdzie maksymalnym momentom towarzyszą znaczne siły tnące. Jeżeli dodatkowo nie stosowano prętów odgiętych, to może wystąpić koniecz­ność zwiększenia ilości zbrojenia głównego, tak aby spełnić warunek T_d ≤ A_s1*f_yd . W przekroju, gdzie m_sd jest bliskie zeru, warunek powyższy określa niezbędną ilość prętów, które muszą dojść do podpory. W zdecydowa­nej jednak większości przypadków wystarcza ilość zbrojenia przyjęta z warun­ków konstruowania podanych dla stanu granicznego nośności na zginanie. Zbrojenie to musi sięgać na odległość równą co najmniej 0,5d ctg0 poza miejsce, gdzie jest niezbędne obliczeniowo.

Ścinanie między średnikiem i półką w przekrojach teowych

W przekrojach teowych, gdy pólka jest ściskana, oś obojętna przechodzi najczęściej niedaleko dolnej krawędzi tej płyty i naprężenia ścinające mają w polce jeszcze dosyć znaczną wartość. Ponieważ ścinanie wynika ze zmiany naprężeń (momentów), średnią silę ścinającą na jednostkę długości oblicza się ze wzoru

V_sd = F_d,max / a_v

gdzie: F_d,max - jest maksymalną wartością obliczeniowej siły podłużnej w półce po jednej stronie średnika.

a_v - odległością pomiędzy miejscami występowania maksymalnego i zerowe­go momentów.

W najbardziej niekorzystnym przypadku w półce naprężenia są stałe i równe -αf_cd W związku z tym wartość V_sd oblicza się ze wzoru

V_sd = αf_cd • (b_eff - b_w) /2 a_v

Siła ta jest przenoszona w przyjętym modelu przez ściskane krzyżulce betonowe (równolegle do osi polki) i rozciągane cięgna stalowe (prostopadłe do osi półki). W belkach teowych rolę tych cięgien spełniają zwykle strzemiona, a w stropach płytowo-żebrowych — zbrojenie górne płyty nad żebrem. Nośność betonowych krzyżulców sprawdza się z warunku

V_sd ≤ V_Rd2 = 0.2*f_cd*h_f

Jeżeli do wyrażenia wstawimy poprzednie to warunek ten okaże się ograniczeniem szerokości półki:

b_eff - b_w ≤ 0.4* a_v

to równanie jest spełnione tożsamościowo

Drugi warunek dotyczy rozciągania i ma postać

V_sd ≤2.5 τ_Rd h_f + A_sf* f_yd /s_f

Praktycznie służy on do wyznaczenia niezbędnego zbrojenia (strzemion) w półce belki Najczęściej rozstaw strzemion s_f ich powierzchnia A_sf są takie same jak wyliczone dla średnika ze względu na ścinanie i szerokość rozwarcia rys ukośnych.

Jeżeli na odcinku a_v pólka jest rozciągana, to we wzorze powyższym należy przyjąć 2.5 τ_Rd h_f =0.

Zasady postępowania przy sprawdzaniu nośności przekrojów ukośnych

Podstawą do sprawdzania stanu granicznego nośności na ścinanie jest wykres sił tnących. W następnej kolejności wyznacza się wartości sił V_Rd1 oraz V_Rd2 i miarodajną siłę tnącą V_sd . W przypadku, gdy obciążenie belki jest równomiernie rozłożone a jej podparcie bezpośrednie, do obliczeń można przyjmować wartość siły tnącej w odległości d od lica podpory. Jeżeli warunki te nie są spełnione (np. podciąg), to miarodajną jest siła tnąca w licu podpory.

Siła V_Rd1 obrazuje nośność na ścinanie przekroju, w którym naprężenia rozciągające jest w stanie przenieść beton. Przy korzystaniu ze wzoru na V_Rd1 należy zwrócić uwagę na fakt, że zbrojenie główne można uwzględnić tylko wtedy, gdy jego pręty są przedłużone (w celu zakotwienia) poza analizowany przekrój o co najmniej l_b,netto .

Jeżeli obliczeniowa siła tnąca V_{sd ≤} V_Rd1 to nie przeprowadza się szczegóło­wych obliczeń ścinania, a jedynie zbroi się przekroje przypodporowe, tak aby spełnić wymagania konstrukcyjne. Siła V_Rd2 jest natomiast maksymalną sili ściskającą, która może powstać w krzyżulcu betonowym (odpowiada kątów nachylenia krzyżulca θ =π /4). Jeżeli siła V_{sd >} V_Rd2 to nie ma możliwości prawidłowego zaprojektowania przekrojów ukośnych. W związku z tym celowe jest uwzględnienie tego ograniczenia na etapie wstępnego przyjmowania wymiarów przekroju (aby uniknąć późniejszej konieczności zwiększania b lub h ) .

W związku z tym obliczenia nośności przekrojów ukośnych przeprowadzi się, gdy spełniony jest warunek

V_{Rd1 ≤} V_{sd ≤} V_Rd2

Kolejnym krokiem (po obliczeniu V_Rd1 jest określenie w jakiej części belki należy obliczać zbrojenie na ścinanie. Zasięg ten oznaczany „l_t" spełnia warunek V_sd (x< l_t) > V_Rd1.

Jeżeli odcinek , „l_t" jest krótki („l_t" < 2d), to oznacza że wpływ ścinania na nośność belki nie jest istotny. W takich przypadkach całą siłę w rozciąganych krzyżulcach mogą przyjąć strzemiona.

W przypadku, gdy odcinek „l_t" jest dłuższy niż 2d lub na odcinku tym występują pręty odgięte, które mogą być uwzględnione przy sprawdzaniu nośności na ścinanie (spełniają wymagania konstrukcyjne), należy odcinek ten podzielić na mniejsze. W sytuacji, gdy występują pręty odgięte, podział odcinka należy dostosować do miejsc występowania tych prętów. Przy wymiarowaniu bierze się do obliczeń maksymalną siłę tnącą dla każdego z tych odcinków. Dzięki temu podziałowi wymiarowanie jest oszczędniejsze.

Jeżeli rozstaw strzemion spełnia wymagania konstrukcyjne, obliczenia stanu granicznego nośności można uznać za zakończone. W przypadku, gdy rozstaw strzemion jest zbyt duży, najprostszym rozwiązaniem jest zmniej­szenie ich średnicy. Gdy natomiast rozstaw s₁ byłby mniejszy niż 5 cm, celowe jest zwiększenie średnicy lub zastosowanie strze­mion czteroramiennych (zbyt gęste strzemiona utrudniają betonowanie).

Praktycznym rozwiązaniem jest ujednolicenie rozstawu strzemion na całym odcinku l, — do najmniejszego z obliczonych s₁. Kosztem niewielkiego wzrostu zużycia stali ułatwia się i przyspiesza konstruowanie szkieletu zbroje­niowego i eliminuje możliwość popełnienia błędów.

Obliczanie elementów żelbetowych na skręcanie.

Moment skręcający wynika z działania sił przyłożonych na mimośrodzie względem osi podłużnej elementu. Efekty towarzyszące skręcaniu mogą wystąpić również w wyniku odkształceń, jako skutek wzajemnego połączenia elementów konstrukcyjnych.

W skutek działania momentu skręcającego T powstają naprężenia ścinające t_T w przekrojach poprzecznych elementów. Rozkład tych naprężeń zależy od kształtu przekroju, a także od kierunku i usytuowania linii przekrojowej.

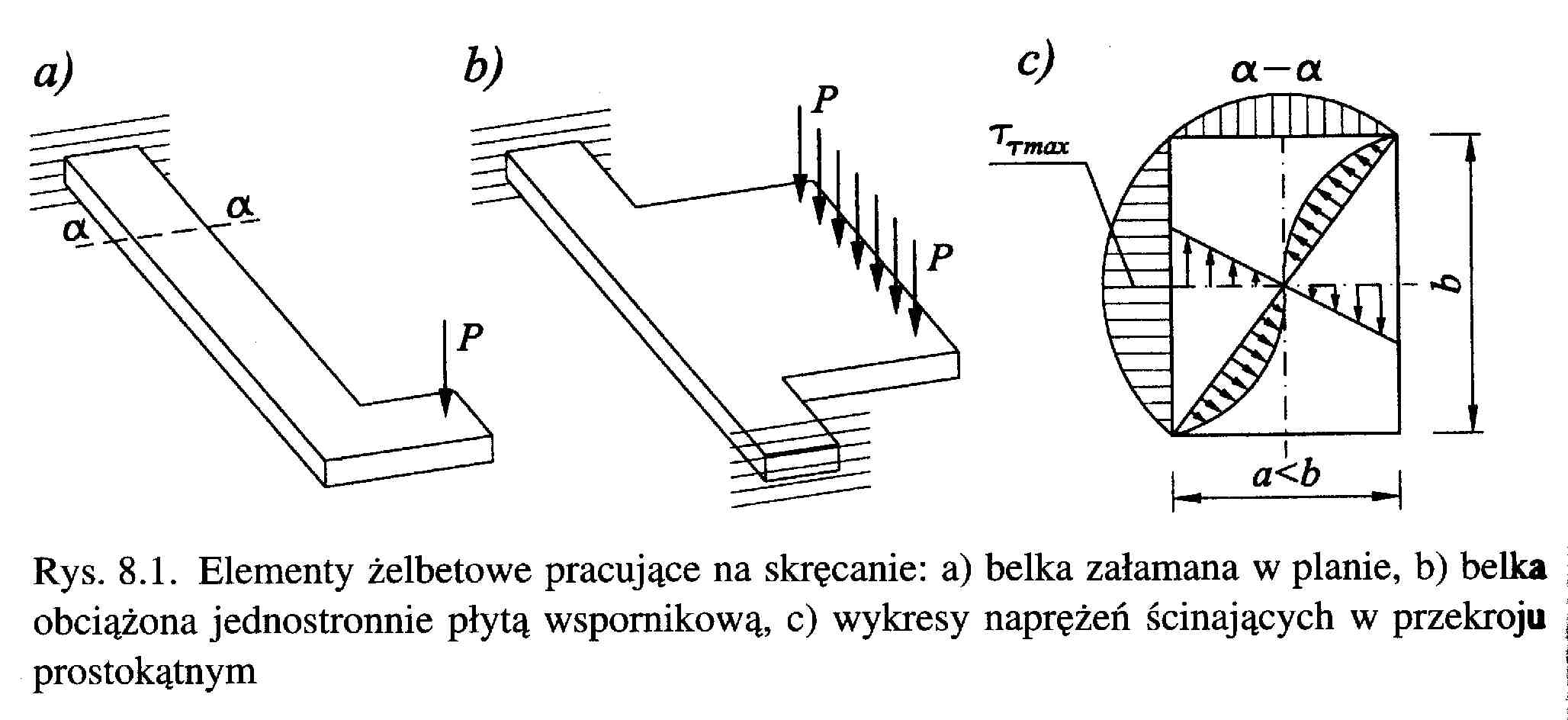
W przekroju o kształcie kołowym skręcanie spowodowane jest liniowym wzdłuż promienia i osiowo symetrycznym stanem naprężeń, co oznacza, że rozkład naprężeń nie zależy od linii przekroju. W prętach pryzmatycznych wykresy naprężeń na poszczególnych krawędziach przekroju są różne.

W przekroju prostokątnym największe naprężenia ścinające powstają przy powierzchni zewnętrznej pręta w środku dłuższego boku przekroju poprzecznego

Model kratownicy przestrzennej w obliczeniach na skręcanie.

Zgodnie z założeniami metody wszystkie przekroje żelbetowe rozpatruje się jako wydrążone przekroje cienkościenne. Wynika to z rezultatów badań doświadczalnych, które wykazują, że po zarysowaniu elementu żelbetowego poddanego skręcaniu beton zawarty wewnątrz przekroju, w pobliżu środka ciężkości elementu, nie osiąga wytrzymałości i nie podlega zarysowaniu, a zatem jego udział może zostać pominięty w obliczeniach.

Sztywność na skręcanie dla przekroju nieprostokątnego otrzymuje się dzieląc przekrój na zespół prostokątów i sumując ich sztywności na skręcanie. Przekrój należy dzielić tak, aby uzyskać maksymalną sztywność.

W omawianej metodzie „grubość” ścianki można wyznaczyć t=A/u gdzie:

u - obwód zewnętrzny przekroju poprzecznego elementu

A - całkowita powierzchnia przekroju elementu

Dla celów obliczeniowych jako model pryzmatycznego pręta skręcanego przyjmuje się kratownicę przestrzenną.

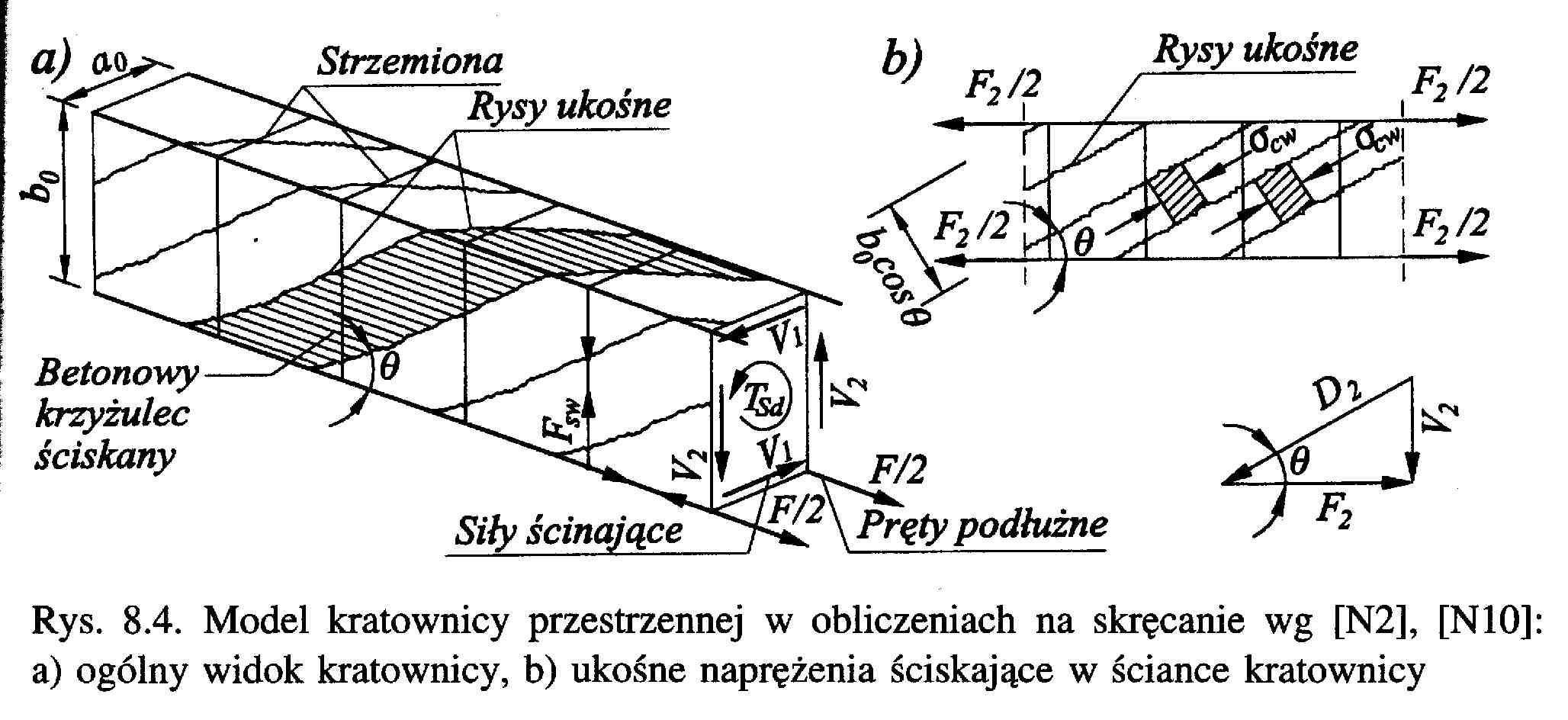
W modelu o którym mowa, element jest zastępowany ustrojem złożonym z:

• podłużnych prętów zbrojenia głównego (umieszczonych w narożach)

• zamkniętych rozciąganych strzemion (prostopadłych lub ukośnych)

• ukośnych ściskanych krzyżulców betonowych nachylonych pod kątem
  do krawędzi poziomych

Czyste skręcanie.

Obliczeniowy moment skręcający powinien spełniać następujące warunki

- z uwagi na ściskane krzyżulce betonowe

- z uwagi na zbrojenie

Jednoczesne skręcanie i ścinanie.

Powinien być spełniony warunek (ze względu na ściskane krzyżulce betonowe):

gdzie:

T_Rd1 - nośność przekroju na skręcanie

V_Rd2 - graniczna siła poprzeczna w funkcji nachylenia betonowych krzyżulców ściskanych

W złożonym stanie obciążeń pole przekroju strzemion wyznacza się niezależnie ze względu na ścinanie, oraz czyste skręcanie.

W przypadku jednoczesnego skręcania i ścinania prętów pryzmatycznych w przekrojach pełnych (o kształcie zbliżonym do prostokątnego) można nie projektować zbrojenia, jeśli jednocześnie spełnione są warunki:

Jednoczesne skręcanie i zginanie.

W takim przypadku należy projektować wymagane zbrojenie podłużne oddzielnie dla każdego rodzaju oddziaływań. Obowiązują tu następujące zasady:

• zbrojenie podłużne na skręcanie w strefie rozciąganej elementu musi być zbrojeniem dodatkowym w stosunku do obliczonego na moment zginający

• zbrojenie podłużne w strefie ściskanej (od zginania) nie wymaga uzupełnienia o pręty podłużne obliczeń na skręcanie, gdy naprężenia od skręcania są mniejsze od naprężeń ściskających od zginania

Zasady projektowania przekrojów poddanych skręcaniu.

W celu zaprojektowania przekroju poddanego czystemu skręcaniu należy postępować jak podano niżej.

• Określić zastępczą grubość t umownej ścianki elementu pełnościennego. W przekrojach skrzynkowych będzie to minimalna grubość ścianki.

• Obliczyć maksymalną nośność T_Rd1 na skręcanie.

• Przy wyznaczonej T_Rd1 sprawdzić nośność z uwagi na beton ściskany.

• Przyjąć średnice strzemion i obliczyć ich rozstaw.

• Sprawdzić minimalny stopień zbrojenia dla strzemion wg zasad obowiązujących dla ścinania.

• Obliczyć pole przekroju zbrojenia podłużnego.

Wymagania konstrukcyjne dla elementów zbrojonych na skręcanie.

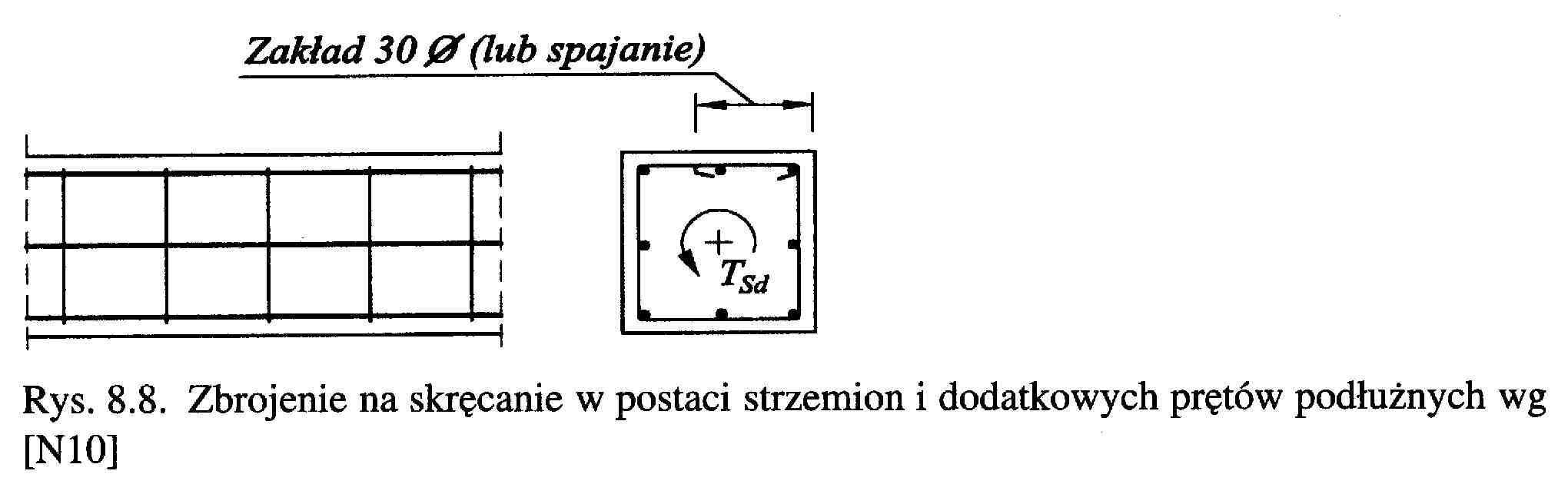
Zbrojenie elementów poddanych czystemu skręcaniu, lub skręcaniu połączonemu ze ścinaniem powinno składać się z dwuramiennych zamkniętych strzemion i dodatkowych (w stosunku do zbrojenia na zginanie) prętów podłużnych rozmieszczonych równomiernie na obwodzie rdzenia elementu.

Stosowanie strzemion czteroramiennych nie jest wskazane z uwagi na to, że ich wewnętrzne ramiona pozostają z reguły poza zastępczą grubością t ścianki elementu i nie przenoszą naprężeń od skręcania. W PN-99 dopuszcza się także konstruowanie zbrojenia na skręcanie w postaci uzwojenia o kierunku zgodnym z kierunkiem działania momentu skręcającego. Stosowanie uzwojenia jest dopuszczalne jedynie wtedy, gdy na przekrój działa moment skręcający jednego znaku. W takim przypadku rozstaw prętów uzwojenia nie powinien przekraczać mniejszego wymiaru przekroju poprzecznego skręcanego elementu.

W elementach skręcanych należy stosować wyłącznie strzemiona zamknięte lub też spajane. Siła ściskająca w betonowych ukośnych krzyżulcach umownej kratownicy będzie przekazana na strzemiona pod warunkiem, że co najmniej jeden pręt podłużny zostanie umieszczony w każdym z naroży skręcanego elementu.

Zarysowanie elementów żelbetowych.

Rysy w konstrukcjach z betonu powstają w efekcie osiągnięcia przez beton wytrzymałości na rozciąganie w określonych przekrojach i strefach elementów.

W pierwszym okresie po wykonaniu przyczyną zarysowania niektórych konstrukcji mogą być tzw. odkształcenia wymuszone, wywołujące w przekrojach elementów niezrównoważone naprężenia termiczne, pochodzące z wewnętrznych pól temperatury związanych z utrata ciepła hydratacji przez dojrzewający beton. Mimo, że naprężenia te dość szybko zanikają, to w młodym betonie o małej jeszcze wytrzymałości na rozciąganie, są one w stanie wywołać trwałe zarysowanie. W belkach i płytach zbrojonych rysy skurczowe mogą powstać jeszcze przed obciążeniem elementu.

Naprężenia pochodzące od zewnętrznych czynników mechanicznych (ciężar własny, obciążenia użytkowe) lub nie mechanicznych (zmiany temp., osiadanie podpór) mogą przyczynić się do powstawania rys eksploatacyjnych o różnym układzie, zagęszczeniu czy rozwartości.

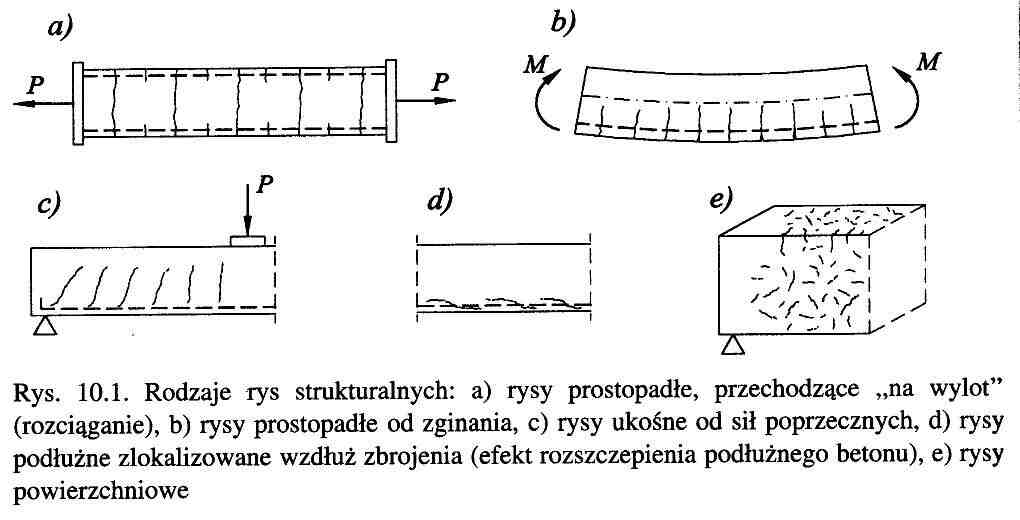
Założenia.

Pola przekrojów, momenty statyczne, wskaźniki wytrzymałości, momenty bezwładności, zasięgi stref ściskanej i rozciąganej, oraz naprężenia w betonie i w zbrojeniu, występujące we wzorach stosowanych przy sprawdzaniu stanów granicznych użytkowalności, oblicza się przyjmując, że przekroje płaskie przed odkształceniem pozostają płaskie po odkształceniu, a stal jest materiałem sprężystym o module E_s. W analizie elementów zarysowanych rozpatruje się I i II fazy obliczeń. W fazie I (element tuż przed pojawieniem się rysy) należy uwzględniać wytrzymałość betonu na ściskanie i rozciąganie. W fazie II (element całkowicie zarysowany) do obliczeń przyjmuje się, że beton nie wykazuje wytrzymałości na rozciąganie, a w strefie ściskanej zachowuje się jak materiał liniowo sprężysty.

Beton i stal traktuje się jako materiały sprężyste, których wzajemna odkształcalność pod obciążeniem krótkotrwałym wyrażona jest współczynnikiem

Natomiast przy obciążeniach długotrwałych wzajemną odkształcalność stali i betonu można opisać współczynnikiem

- końcowy współczynnik pełzania betonu

Wymagania w zakresie zarysowania konstrukcji.

W obliczeniach zarysowanych konstrukcji żelbetowych należy spełniać wymagania stawiane przez normę w zakresie stanu granicznego użytkowalności. Trzeba wykazać, że w konstrukcji nie pojawią się rysy nadmiernie rozwarte, niedopuszczalne z uwagi na trwałość i estetykę. Odpowiedni warunek stanu granicznego zarysowania zapisujemy

gdzie: w_k - obliczenia szerokość rysy

w_lim - graniczna szerokość rysy prostopadłej bądź ukośnej

W niektórych typach konstrukcji żelbetowych, jak zbiorniki na ciecze, a także w przypadku ścian oporowych, przecieki wody są niedopuszczalne, zatem w tych przypadkach powstanie bardziej rozwartych rys grozi wstrzymaniem eksploatacji obiektów.

Zgodnie z wymaganiami PN-99 obliczenia dotyczące zarysowania należy przeprowadzić , przyjmując kombinację obciążeń długotrwałych. W przypadku elementów projektowanych w środowisku klasy 5 wymagane są specjalne ograniczenia w zakresie szerokości rys z uwagi na oddziaływania chemicznie agresywne.

Tablica 10.1 Graniczne szerokości rys w konstrukcjach żelbetowych wg [N10]

Wymagania użytkowe	Klasa środowiska wg tabl. 2.20	Graniczna szerokość rysy w^ [mm]
Ochrona przed korozją	5bi5c	O,1^1)
		3, 4a, 4b, 5a	0,2
		l i2	0,3
Zapewnienie szczelności		O,1^1)

¹⁾ Jeżeli przepisy szczegółowe nie stanowią inaczej

Szerokość rys prostopadłych w elementach zginanych o przekroju prostokątnym zbrojonych stalą żebrowaną można uważać za nie większą niż w_lim, jeżeli maksymalna średnica prętów podłużnych zbrojenia rozciąganego nie przekracza F_max określonego odpowiednią tabelką w normie.

Wyznaczanie szerokości rys.

N_cr=f_ctmA_c - siła rysująca element osiowo rozciągany

M._cr=f_ctmW_ct - wartość momentu rysującego przy zginaniu

- siła rysująca przy rozciąganiu mimośrodowym

Szerokość rys prostopadłych.

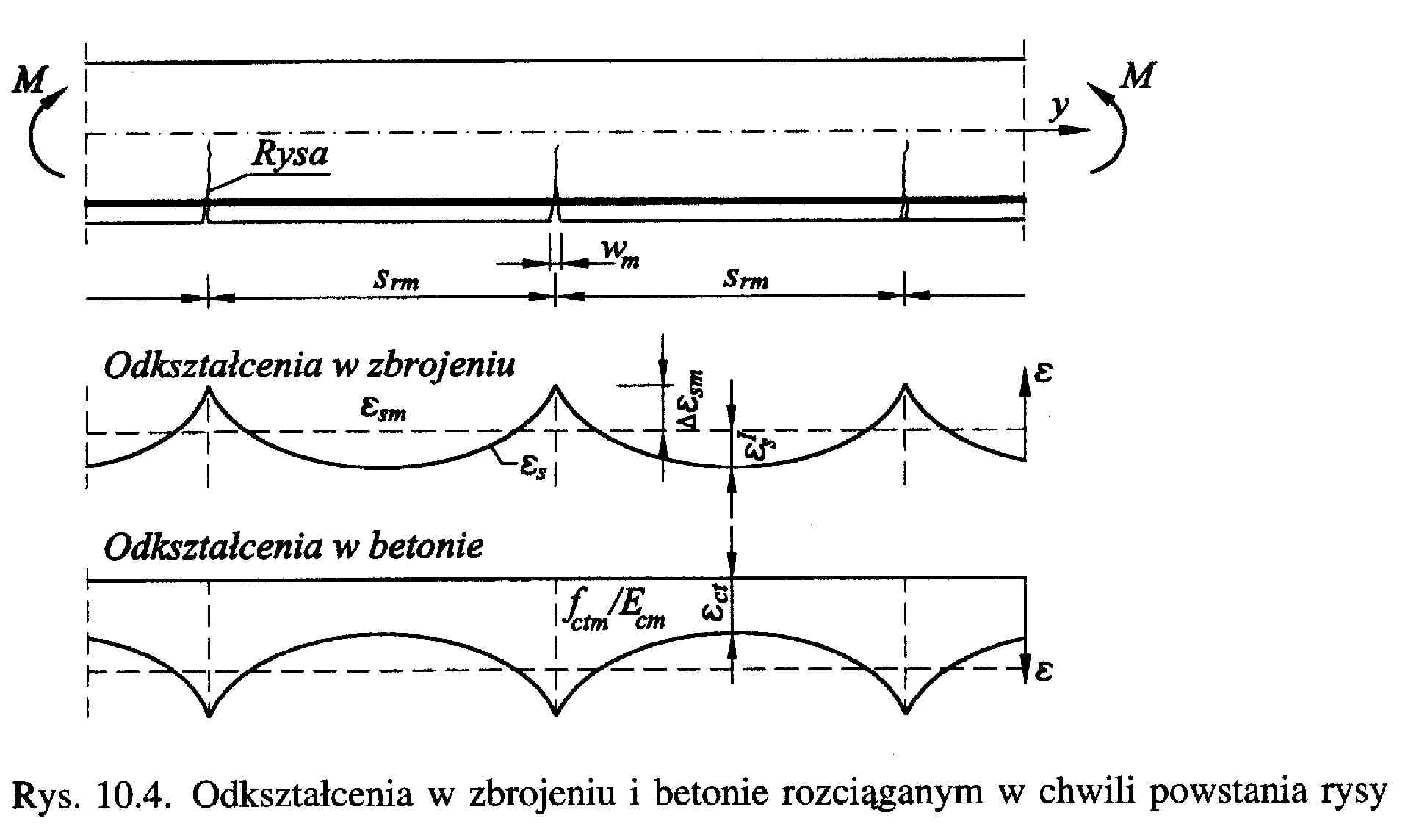
Szerokość rys oblicza się na podstawie uśrednionych wartości odkształceń w betonie i stali zbrojeniowej. Można tu wykorzystać założenia przedstawione na rysunku poniżej.

Całkując różnicę odkształceń stali i betonu na odcinku między rysami, wyznaczamy średnią szerokość rysy.

- obliczeniowa szerokość rys prostopadłych do elementu

- współczynnik wyrażający stosunek obliczeniowej szerokości rys do szerokości średniej

s_rm - średni końcowy rozstaw rys

- średnie odkształcenie zbrojenia rozciąganego

Rozstaw rys.

Przyrostowi naprężeń w prętach zbrojenia w przekroju przez rysę 1-1 towarzyszy wzrost naprężeń przyczepności w pręcie na odcinku nieznanej długości s_r. Założenia do obliczeń podano na rysunku poniżej.

Po obu stronach rysy w przekroju 1-1 naprężenia w zbrojeniu maleją dzięki zjawisku przyczepności, rosną natomiast w betonie strefy rozciąganej, która przenosi część siły rozciągającej F_ct. Nowa rysa powstanie w przekroju 2-2, który ustala się w poszukiwanej odległości s_r od zarysowanego przekroju 1-1. Powstaniu rysy towarzyszą naprężenia w betonie równe wytrzymałości betonu na rozciąganie f_ctm.

Szerokość rys ukośnych.

W PN-99 zezwala się odstąpić od obliczania szerokości rys ukośnych w przekrojach elementów żelbetowych (dla których w_lim=0,3mm), jeżeli nośność na ścinanie tych elementów została osiągnięta wyłącznie w wyniku zastosowania strzemion pionowych ze stali klasy A-0 o średnicy mniejszej, bądź równej 8mm, a kąt nachylenia krzyżulców betonowych jest większy, bądź równy 29,7⁰.

Minimalne pole przekroju zbrojenia.

Minimalne pole przekroju zbrojenia rozciąganego, wymagane z uwagi na ograniczenie szerokości rys spowodowanych naprężeniami wywołanymi przez odkształcenia wymuszone przyczynami wewnętrznymi (skurcz), lub zewnętrznymi (osiadanie podpór) - wyznacza się z odpowiedniego wzoru normowego.

Ugięcia elementów żelbetowych niezarysowanych i zarysowanych.

Stosowanie w rozwiązaniach konstrukcyjnych wyższych klas betonu i stali zbrojeniowej pozwala realizować bardziej materiałooszczędne, lecz jedno­cześnie coraz bardziej wiotkie elementy nośne. W wyniku działających obciążeń ustroje mogą podlegać przemieszczeniom, które w procesie projektowania muszą być uwzględniane i kontrolowane w ramach weryfi­kacji stanu granicznego użytkowalności.

Ugięcie należy zatem traktować jako maksymalne przemieszczenie elementu, będące odpowiedzią konstrukcji na przyłożone obciążenie. Kon­trola ugięć spowodowanych działaniem obciążeń użytkowych ma istotne znaczenie z uwagi na następujące przesłanki eksploatacyjne:

— zapewnienie użytkowalności konstrukcji,

— możliwość uszkodzeń przylegających elementów niekonstrukcyjnych,

— odczucia estetyczne użytkowników.

Nadmierne ugięcia elementów konstrukcyjnych w niektórych przypadkach mogą być przyczyną utraty zdolności eksploatacyjnych przez konstrukcję, jak to ma miejsce np. w nadmiernie ugiętych płytach stropodachów, co może prowadzić do powstawania zastoisk wody opadowej na połaci dachu. Bardzo ważną przesłanką jest możliwość uszkodzenia elementów przylegających do nadmiernie odkształconych konstrukcji nośnych. Może to mieć miejsce w przypadku ich kontaktu ze ściankami działowymi, oszklonymi przegrodami lub zamocowanymi detalami wykończenia. Odkształcenia mogą też ograni­czać lub wręcz uniemożliwiać funkcjonowanie drzwi lub okien stykających się z elementami nośnymi. Nie bez znaczenia może być także pogorszenie estetyki wnętrza, w którym np. elementy stropowe są nadmiernie ugięte.

Na ugięcia elementów żelbetowych wpływa wiele czynników, z któ­rych większości nie udaje się uwzględnić w obliczeniach w sposób ścisły. Podstawowe znaczenie ma tu czas, z czym wiążą się głównie skurcz i pełzanie betonu oraz relaksacja stali zbrojeniowej. Dlatego też w więk­szości norm postuluje się uwzględnienie ugięć elementów wywołanych kombinacją obciążeń długotrwałych. Ugięcia powstają zarówno w wyniku działania obciążeń bezpośrednich, jak i pośrednich (np. pól temperatury). Obciążenia termiczne mogą niekiedy powodować przemieszczenia ustroju większe niż obciążenia mechaniczne. Ma to np. miejsce w cylindrycznych żelbetowych ścianach zbiorników na ciecze czy w silosach.

W ujęciu ogólnym weryfikacja stanu granicznego ugięć konstrukcji żelbetowych polega na wykazaniu, że ugięcia a elementu (pod wpływem założonej kombinacji obciążeń eksploatacyjnych) nie przekraczają warto­ści granicznych, traktowanych jako dopuszczalne.

Według PN-99 sprawdzanie ugięć jest konieczne w konstrukcjach żelbetowych dachowych i stropowych w budownictwie mieszkaniowym, przemysłowym, rolniczym, a także użyteczności publicznej. W innych przypadkach należy kontrolować ugięcia jedynie tych elementów, dla których sformułowano takie wymaganie w warunkach eksploatacji.

W celu częściowej lub całkowitej kompensacji ugięć zezwala się nadawać elementom konstrukcyjnym odwrotną strzałkę ugięcia, której wartość nie może jednak przekroczyć 1/250 rozpiętości obliczanego ele­mentu.

Ugięcia elementów niezarysowanych

W obliczeniowym modelu liniowo-sprężystym przemieszcze­nie a(y) niezarysowanego elementu prętowego może być wyznaczone na podstawie krzywizny, która w przypadku zginania może być obliczona z uproszczonego równania osi odkształconej.

Rys. 11.2. Krzywizna i ugięcie elementu zginanego bez zarysowania (w fazie I)

Na tej podstawie można sformułować normowy wzór obowiązujący przy wyznaczeniu maksymal­nych ugięć w elementach zginanych

gdzie:

a_k - współczynnik zależny od rozkładu momentu zginającego

B - sztywność przekroju elementu odpowiadająca momentowi obliczeniowemu M._Sd (wg. załącznika E)

B_oo=E_c,effJ_I - dla długotrwałych (uwzględnione pełzanie betonu)

B_o=E_cmJ_I - dla krótkotrwałych

W przeciwieństwie do Eurokodu 2 w PN-99 nie nałożono obowiązku obliczania w elementach żelbetowych ugięć wywołanych skurczem betonu, jakkolwiek jest to wymagane przy obliczaniu elementów zespolonych.

Rys. 11.6. Sprowadzony przekrój prostokątny w fazie I

Ugięcia elementów zarysowanych

Jak wyjaśniono to wcześniej, w elemencie zarysowanym sztywność ulega zasadniczym zmianom na długości elementu, przy czym wyraźne różnice obserwuje się nawet w sąsiednich przekrojach. Zmiany sztywności B_II w zarysowanym elemencie zginanym obciążonym siłą skupioną pokazano schematycznie na rys. 11.3.

Rys. 11.3. Wpływ zarysowania na spadek sztywności zginania elementu

Jest oczywiste, że uwzględnienie rzeczywistej funkcji zmiany sztywności na długości elementu poważnie komplikuje obliczanie ugięć. W obliczeniach inżynierskich można stosować założenia upraszczające, które polegają na uśrednieniu sztywności przekrojów na odcinku między rysami oraz sztywności w przekrojach przechodzących przez rysy (tak, jak pokazano to linią przerywaną na rys. 11.3). W jeszcze większym uproszczeniu możliwe jest uśrednienie sztywności na długości elementu.

Sztywność elementu zarysowanego przy obciążeniu długotrwałym można wyznaczyć ze wzoru

Sztywność elementu zarysowanego przy obciążeniu krótkotrwałym można wyznaczyć ze wzoru

Wartości współczynników doświadczalnych
przyjmuje się podobnie jak w przypadku obliczania szerokości rys prostopadłych przy zginaniu. I tak w zależności od przyczepności zbrojenia do betonu:

— dla prętów żebrowanych
= 1,0,

— dla prętów gładkich
= 0,5.

W zależności od czasu działania i powtarzalności obciążenia:

— dla jednokrotnego obciążenia krótkotrwałego
= 1,0,

— dla obciążeń długotrwałych lub wielokrotnie powtarzalnych
= 0,5. W

Rys. 11.7. Sprowadzony przekrój prostokątny w fazie II

Na ogół obciążenie krótkotrwałe działa na element, który ugiął się wcześniej pod wpływem obciążeń długotrwałych. Wartości graniczne ugięć, wywołanych jednoczesnym działaniem tych dwóch rodzajów obciążeń, nie są określone w tej normie - jeżeli zachodzi taka potrzeba, to ustala się je stosownie do wymagań w rozpatrywanym przypadku.

Maksymalne ugięcie można obliczyć ze wzoru:

a=a_0,k+d-a_0,d+a_oo,d

w którym:

a_0,k+d - ugięcie, które powstałoby natychmiast po jednoczesnym przyłożeniu obciążeń krótko i długotrwałych -

sztywność B₀

a_0,d - ugięcie, które powstałoby natychmiast po przyłożeniu obciążeń długotrwałych - sztywność B₀

a_oo,d - ugięcie długotrwałe, wywołane obciążeniami długotrwałymi - sztywność B_oo

Projektowanie i sprawdzanie nośności żelbetowych elementów ściskanych przy małym i dużym mimośrodzie.

Termin „elementy ściskane" odnosi się do konstrukcji takich, jak słupy lub tarcze ścienne, które podlegają działaniu podłużnych sił ściskających w połączeniu ze zginaniem, co prowadzi do ściskania mimośrodowego. Mimośrody towarzyszą w praktyce pracy wszystkich ustrojów budow­anych, np. z uwagi na oddziaływanie momentów zginających pochodzących od obciążeń zewnętrznych. Występują też mimośrody przypadkowe, nie zamierzone przez projektanta, spowodowane np. imperfekcjami geometrycznymi samego elementu lub węzła mocującego element. Z tego punktu widzenia wyeliminowany został z obliczeń inżynierskich przypadek „osiowego ściskania". W elementach konstrukcyjnych z betonu obciążonych podłużną siłą ściskającą istotny wpływ na zachowanie się ustroju mają efekty II rzędu.

Elementy żelbetowe.

W ślad za Eurokodem 2 również w PN-99 wprowadza się klasyfikację żelbetowych elementów ściskanych smukłych, w przypadku których niezbędne jest uwzględnienie efektów II rzędu. W ustrojach tych wskaźnik smukłości

i

Jeżeli powyższe zalecenia nie są spełnione, to elementy ściskane uznaje się za krępe, a projektant nie ma obowiązku uwzględnienia efektów II rzędu.

Obliczeniową długość l₀ elementu ściskanego, niezbędną do określenia smukłości wg normy PN-99, można ustalać zgodnie z zasadami teorii sprężystości liniowej. Długości obliczeniowe l₀ słupów mogą być przyjmowane według załącznika C.

W celu uwzględnienia efektów II rzędu (wpływu smukłości) w przepi­sach polskich utrzymane zostało obowiązujące od 1976 r. zalecenie, zgodnie z którym mimośród statyczny (I rzędu) należy powiększyć o mimośród e_a wyrażający imperfekcje słupa, a następnie sumę obu mimośrodów pomnożyć przez współczynnik
, nie mniejszy od jedności. Od­powiedni zapis ma postać

e_e - mimośród statyczny - różne wzory w zależności od kształtu wykresu momentów zginających (prosto czy krzywoliniowy) i czy węzły są przesuwne czy nieprzesuwne

e_a - mimośród niezamierzony - w zależności od typu konstrukcji, długości l_col elementu oraz wysokości h przekroju poprzecznego

Nośność przekrojów podporowych słupów w układach nieprzesuwnych obciążonych momentami należy sprawdzać bez uwzględnienia wpływu smukłości.

Metoda ogólna. - kij jej w oko, nie ma jej w normie, a poza tym to zbyt porąbane - (wyktesy naprężeń paraboliczno - prostokątne podobne jak w ogólnej dla rozciągania)

Na podstawie odkształceń granicznych betonu i stali zbrojeniowej w konstrukcjach ściskanych wprowadza się dwa podstawowe przypadki obliczeniowe związane z wartością mimośrodu e₀ działania siły podłużnej ściskającej. Dotyczy to:

— dużego mimośrodu, gdy spełniony jest warunek ogólny zasięgu strefy ściskanej przekroju

— małego mimośrodu, gdy spełniony jest warunek

W obu przypadkach
to graniczna wysokość strefy ściskanej prze­kroju wyznaczana wg zasady płaskich przekrojów. Zniszczenie przekroju przy dużym mimośrodzie powoduje uplastycznienie zbrojenia rozciąganego (ang. tension failure), co w konsekwencji pozwala na pełne wykorzystanie przekroju tego zbrojenia. Natomiast w przypadku małego mimośrodu zbrojenie rozciągane nie osiąga granicy plastyczności, a znisz­czenie przekroju następuje wskutek wyczerpania nośności betonu w strefie ściskanej (ang. compression failure).

Metoda uproszczona obliczeń elementów ściskanych.

W obliczeniach żelbetowych przekrojów mimośrodowo ściskanych dopu­szcza się stosowanie metody uproszczonej. Główne założenie tej metody polega na przyjęciu prostokątnego wykresu naprężeń na całej powierzchni strefy ściskanej, której efektywny zasięg x_eff jest zredukowany do wartości 0,8x.

W metodzie uproszczonej nie jest wymagane zachowanie warunku zgodności odkształceń w betonie i zbrojeniu przekroju, co w metodzie ogólnej wynika wprost z zasady płaskich przekrojów. W projektowaniu elementów ściskanych zarówno metodą uproszczoną, jak i ogólną, rozpat­ruje się przypadki obliczeniowe dotyczące:

— dużego mimośrodu, gdy spełniony jest warunek

• małego mimośrodu, gdy spełniony jest warunek

W przypadku dużego mimośrodu, gdy na przekrój dowolny działa siła ściskająca na mimośrodzie względem środka ciężkości przekroju, układ sił wewnętrznych od obciążeń, zgodnie z zasadami metody uprosz­czonej, można przedstawić jak na rys. 4.17. Widać, że dowolny przekrój elementu obciążonego mimośrodowo pozostaje w równowadze pod działa­niem następujących sił wewnętrznych:

F_c=A_cc,effaf_cd — wypadkowej naprężeń ściskających beton w strefie ściskanej przekroju

F_s2=A_s2f_yd — wypadkowej naprężeń w zbrojeniu umieszczonym w strefie ścis­kanej

F_s1=A_s1f_yd — wypadkowej naprężeń w zbrojeniu umieszczonym w strefie rozciąganej

Rys. 4.17. Wykres naprężeń i układ sił wewnętrznych w przypadku dużego mimośrodu (metoda uproszczona)

Ze wzoru na wypadkową zbrojenia A_s2 wynika, że w metodzie uprosz­czonej — niezależnie od zasięgu efektywnej strefy ściskanej — przyjmuje się naprężenia w tym zbrojeniu równe granicy plastyczności f_yd. Przy takich założeniach (podobnie jak w metodzie ogólnej) przekroje ściskane w przypadkach dużego mimośrodu wymiaruje się według zasad obowiązu­jących dla zginania.

Na rysunku 4.18 przedstawiono układ sił wypadkowych w przekroju w przypadkach małego mimośrodu, które występują z reguły wówczas, gdy siła podłużna przyłożona jest między środkami ciężkości zbroje­nia ściskanego i rozciąganego.

Rys. 4.18. Wykres naprężeń i układ sił wewnętrznych w przypadku małego mimośrodu (metoda uproszczona)

Wartość współczynnika k_s wyznacza się z normowych wzorów w zależności od
i przyjmuje on wartość

Nośność elementów ściskanych mimośrodowo symetrycznych względem płaszczyzny zginania należy sprawdzać z warunku równowagi sumy momentów sił zewnętrznych i wewnętrznych względem osi zbrojenia A_s1.

Zasięg efektywnej strefy ściskanej wyznacza się z warunku równowagi sumy rzutów siły podłużnej oraz wypadkowych sił wewnętrznych na oś podłużną elementu ściskanego.

przy czym w przypadku dużego mimośrodu współczynnik k_s z definicji należy przyjmować jako równy +1.

Projektowanie i sprawdzanie nośności elementów żelbetowych rozciąganych.

W żelbetowych elementach konstrukcyjnych rozciąganie może wystę­pować bez udziału momentu zginającego (osiowe rozciąganie) lub przy jego udziale (mimośrodowe rozciąganie). Przykłady konstruk­cji żelbetowych poddanych rozciąganiu pokazano na rys. 5.1. Osio­we rozciąganie występuje np. w pasach dolnych żelbetowych kratow­nic, ściągach żelbetowych, środkowych pasmach ścian cylindrycz­nych zbiorników na ciecze lub silosów. W strefach podporowych takich ustrojów z reguły na stan naprężeń ma wpływ moment zgina­jący, co w efekcie odpowiada przypadkowi mimośrodowego rozcią­gania.

Rys. 5.1. Przykłady ustrojów żelbetowych rozciąganych: a) rama ze słupem rozciąganym, b) ściana zbiornika cylindrycznego, c) ściana zbiornika prostopadłościennego

W elementach podlegających działaniu podłużnych sił rozciągających nie uwzględnia się efektów wynikających z wyboczenia. Wynika to stąd, że nieosiowo przyłożona siła rozciągająca nie powoduje przyrostu ugięć elementów, które to zjawisko obserwuje się przy ściskaniu. Dlatego też w obliczeniach elementów rozciąganych pomija się wpływ imperfekcji (mimośrodów przypadkowych), której uwzględnienie jest obowiązkowe przy ściskaniu.

W ustrojach żelbetowych poddanych rozciąganiu powstają rysy prosto­padłe do osi podłużnej elementu, mogące przecinać „na wylot" cały jego przekrój poprzeczny.

Niezbędna jest tu zatem dokładna analiza stanu zarysowania, zwłaszcza w przypadku środowiska agresywnego w stosunku do stali lub betonu.

Z uwagi na wielkość mimośrodu działania siły rozciągającej e = M_Sd/N_Sd rozróżnia się następujące przypadki obliczeniowe (rys. 5.2):

a) rozciąganie osiowe (przy e —> 0),

b) rozciąganie z małym mimośrodem, gdy punkt przyłożenia siły roz­ciągającej N_Sd znajduje się między środkami ciężkości zbrojenia,

c) rozciąganie z dużym mimośrodem, gdy punkt przyłożenia siły N_Sd zlokalizowany jest poza odcinkiem łączącym środki ciężkości zbrojenia.

Rys. 5.2. Przypadki obliczeniowe w przekrojach elementów rozciąganych (opis w tekście)

W przypadkach a) i b) (rys. 5.2a i 5.2b) w przekroju elementu nie występuje strefa ściskana, co oznacza, że całość naprężeń pochodzących od obciążeń musi być przekazana na zbrojenie rozciągane. W przypadku pokazanym na rys. 5.2c występuje strefa ściskana i jej zasięg decyduje o nośności przekroju.

Podobnie jak w elementach zginanych lub ściskanych mimośrodowo w PN-99 (za Eurokodem 2) preferuje się obliczanie nośności przekrojów rozciąganych metodą ogólną na podstawie założeń stanu granicznego nośności i z uwzględnieniem modelu odkształceniowego betonu i stali zbrojeniowej.

W przypadkach a) i b), czyli w przekrojach bez strefy ściskanej, należy:

- przyjąć założenie o płaskich przekrojach,

- pominąć pracę betonu na rozciąganie,

- przyjąć graniczne wartości odkształceń w zbrojeniu rozciąganym (e_S1 = 10,0%0) i uwzględnić bilinearny wykres

dla stali zbrojenio­wej.

Dla przypadku obliczeniowego c) zakłada się graniczne wartości od­kształceń w betonie ściskanym (e_c = 3,5%0) przy paraboliczno -prostokątnym wykresie
w betonie.

W PN-99 zezwolono również na prowadzenie obliczeń metodą uproszczoną, zgodnie z którą w przekrojach rozciąganych z dużym mimośrodem i można korzystać z prostokątnego wykresu naprężeń w strefie ściskanej. Poniżej zostaną omówione oddzielnie metody ogólna i uproszczona.

Metoda ogólna obliczeń. - kij jej w oko (ale jak ktoś ciekaw, to ma wykresy naprężeń)

Mechanizm zniszczenia przekroju rozciąganego osiowo lub z małym mimośrodem wynika z założenia, zgodnie z którym pomija się wytrzyma­łość betonu na rozciąganie. W tych przypadkach występuje specyficzny stan odkształceń i naprężeń, który dla przekroju o dowolnym kształcie pokazano na rys. 5.3. Cały przekrój elementu podlega rozciąganiu, a fik­cyjna strefa ściskana x. położona jest poza tym przekrojem.

W stanie granicznym nośności zbrojenie A_s1 (położone bliżej siły rozciągającej) osiąga odkształcenia graniczne e_s1 = 10%o. Odkształcenia w zbrojeniu A_s2 (mniej rozciąganym) związane są z odkształceniami e_s1 i zgodnie z zasadą płaskich przekrojów zależą od zasięgu fikcyjnej strefy ściskanej x_f. Równania równowagi sił przekrojowych wg oznaczeń poda­nych na rys. 5.3 można zapisać

N_Sd-F_s1-F_s2=0 N_Sde_s1-F_s2(d-a₂)=0

Rys. 5.3. Wykresy odkształceń i naprężeń w przekroju rozciąganym bez strefy ściskane

W analizowanym przekroju dowolnym oblicza się moment M_Sd1=N_Sd(e-y_c+a₁) siły podłużnej N_Sd względem środka ciężkości zbrojenia bardziej rozciąganego. Jeżeli spełniony jest warunek M_Sd1>0 to w przekroju występuje rzeczywista strefa ściskana o zasięgu x, a przekrój podlega rozciąganiu z dużym mimośrodem. Można tu wyróżnić trzy fazy odkształceń: 1a, 1b oraz 2.

Rys. 5.4. Rozkłady naprężeń w różnych zakresach odkształceń w przekroju rozciąganym z dużym mimośrodem

Równania równowagi sił i momentów w przekroju rozciąganym z dużym mimośrodem można zapisać:

F_c+F_s2-F_s1+N_Sd=0 M_Sd1-F_cz_c-F_s2(d-a₂)=0

Wypadkowa F_s2 naprężeń w zbrojeniu ściskanym zależy od jego odkształceń. W celu wyznaczenia wielkości odkształceń należy posłużyć się liniową proporcją wynikającą z zasady płaskich przekrojów. Postępowanie jest tu identyczne jak przy zginaniu.

Metoda uproszczona.

Definicje małego i dużego mimośrodu w metodzie uproszczonej obliczeń przekrojów rozciąganych są identyczne jak w metodzie ogólnej. Ponadto takie same są założenia do wymiarowania przy osiowym rozciąganiu i rozciąganiu z małym mimośrodem.

Zastosowanie metody uproszczonej (prostokątny wykres naprężeń w strefie ściskanej) ułatwia natomiast obliczenia w algorytmie projekto­wania przekrojów rozciąganych z dużym mimośrodem. Układ sił działają­cych na rozciągany przekrój prostokątny (wg założeń metody uprosz­czonej) pokazano na rys. 5.7. Zgodnie z tymi założeniami nośność prze­krojów rozciąganych z dużym mimośrodem określa się z równania równo­wagi momentów sił wewnętrznych względem osi zbrojenia rozciągane­go A_s1. Dla przekroju dowolnego z jedną płaszczyzną symetrii zapiszemy warunek

N_Sde_s1<S_cc,efff_cd+A_s2(d-a₂)f_yd

Rys. 5.7. Układ sił przy rozciąganiu z dużym mimośrodem (metoda uproszczona)

Zasięg efektywnej strefy ściskanej, określający moment statyczny strefy, oblicza się z równania równowagi sił w kierunku osi podłużnej elementu.

Jeżeli x_eff
2a₂ to nośność przekroju należy odliczyć w warunku N_Sde_s2
A_s1f_yd(d-a₂) - mały mimośród. Pomijamy beton na ściskanie.

Elementy rozciągane osiowo.

Minimalny stopień zbrojenia na rozciąganie 0.2% przy każdej z dwu przeciwległych stron elementu.

Obliczanie elementów żelbetowych w strefie obciążeń lokalnych: przebicie, docisk.

1. przebicie

W przypadku działania na konstrukcję siły skupionej (np. od słupa), obciążenia skupionego ciągłego (np. od ściany podłużnej) lub też obciążenia ciągłego rozłożonego stosunkowo na niewielkiej powierzchni, należy sprawdzić nośność tej konstrukcji na przebicie. Najczęściej ma się do czynienia z tym zjawiskiem w płytach opartych na słupach bezpośrednio lub za pośrednictwem głowic - przy braku zbrojenia zaprojektowanego na siły przebicia, oraz w przypadku stóp bądź płyt fundamentowych.

Nośność na przebicie należy sprawdzać w przekrojach ukośnych poprowadzonych pod kątem nie mniejszym niż 45^o od krawędzi powierzchni, na którą działa obliczeniowa siła N_Sd , do poziomu płaszczyzny zbrojenia.

Sposób wyznaczania powierzchni przebicia przedstawiono na poniższych rysunkach.

Nośność elementów bez zbrojenia na przebicie obciążonych w sposób ciągły, w przybliżeniu symetryczny, można obliczać wg wzoru:

N_Sd - (g+q)*A ≤ N_Rd = f_ctd* u_p*d

gdzie:

A - pole powierzchni odciętej przekrojami przebicia w poziomie (średnim) zbrojenia na zginanie

(prostokąt ABCD), na rys. 7.9.

g, q - obciążenie równomierne lub odpór podłoża,

u_p - średnia arytmetyczna obwodów: powierzchni na którą działa siła i powierzchni powstającej w poziomie zbrojenia przy założeniu, rozkładu sił pod kątem 45^o,

d - wysokość użyteczna; jako d należy przyjmować wartość średnią dla kierunków x i y.

W przypadku elementów, w których przebicie może nastąpić tylko w przekrojach nachylonych pod kątem większym niż 45^o (np. płyta fundamentowa oparta na palach ( rys. 7.11.) , obliczenie na przebicie można przeprowadzić na podstawie wzoru:

N_Sd ≤ N_Rd = f_ctd* u_p* d* tan α

w którym:

tan α =d/a lecz nie więcej niż 2,5

a - długość odcinka na rys. 7.11.

W przypadku mimośrodowo obciążonych stóp fundamentowych nośność na przebicie można sprawdzać ze wzoru:

N_Sd = q _max *A ≤ N_Rd = f _ctd * b_m*d

gdzie:

q _max - największy krawędziowy obliczeniowy odpór jednostkowy podłoża (rys. 7.12.)

A - pole powierzchni wielokąta ABCDEF

b_m - średnia arytmetyczna szerokości b₁ i b₂ wg rys. 7.12.

Nośność elementów zbrojonych na przebicie należy sprawdzać z warunków:

N_Sd ≤ N_Rd = 1,4*f_ctd*u_p*d

N_Sd ≤ N_Rd = ΣA_sw1f_ywd + ΣA_sw2f_yw2 sin α

w których:

ΣA_sw1f_ywd - suma sił w strzemionach prostopadłych do płaszczyzny płyty,

ΣA_sw2f_yw2 sin α - suma rzutów sił w prętach odgiętych i w strzemionach nachylonych na kierunek prostopadły do

płaszczyzny płyty.

Zasady konstruowania zbrojenia na przebicie

Zgodnie z normą PN-99 stopień zbrojenia podłużnego elementów sprawdzanych na przebicie nie może być mniejszy niż 0,005 w obu kierunkach.

Zbrojenie to powinno się składać ze strzemion prostopadłych lub ukośnych bądź z prętów ukośnie odgiętych.

Kąt nachylenia zbrojenia ukośnego powinien spełniać warunek: 30^o ≤ α ≤ 60^o.

2. docisk

Nośność przekrojów poddanych działaniu obciążeń miejscowych należy sprawdzać przy założeniu, że wytrzymałość betonu na docisk f_cud zależy od stosunku powierzchni docisku, tj. powierzchni, na którą przykładane jest obciążenie miejscowe, do powierzchni rozdziału tj. powierzchni współpracującej przy przenoszeniu tego obciążenia.

Wytrzymałość betonu na docisk należy obliczać wg wzoru:

- dla elementu niezbrojonego na docisk:

f_cud = ν_cu f*_cd

gdzie:

f*_cd - obliczeniowa wytrzymałość betonu na ściskanie w elementach bez zbrojenia

ν_cu - współczynnik obliczany z wyrażenia:

- dla elementu zbrojonego na docisk:

f_cud = ν_cu f_cd

gdzie:

f_cd - obliczeniowa wytrzymałość betonu na ściskanie

W powyższych wzorach:

lecz nie więcej niż ω_u,max wg tablicy 14 PN-99, przy czym

A_co - pole powierzchni docisku rys.30

A_c1 - pole powierzchni rozdziału rys. 30

σ_cum - średnie naprężenie ściskające na powierzchni rozdziału poza powierzchnią docisku rys. 30

Elementy niezbrojone na docisk należy sprawdzać z warunku:

N_Sd ≤ N_Rd = α_u f_cud A_co

w którym:

N_Sd - siła działająca prostopadle na powierzchnię docisku A_co wyznaczona dla miarodajnej kombinacji obciążeń

obliczeniowych,

α_u - współczynnik zależny od rozkładu obciążenia na powierzchni docisku, określony wzorem:

gdzie:

σ_u,min i σ_u,max - odpowiedni minimalne i maksymalne naprężenia docisku.

Elementy zbrojone na docisk należy sprawdzać z warunku:

N_Sd ≤ N_Rd = α_u f_cud A_co + k f_yd A_u

w którym:

k - współczynnik efektywności zbrojenia na docisk ( np. dla siatek k=1,5)

f_.yd - granica plastyczności stali zbrojeniowej

A_u - zastępcze pole powierzchni zbrojenia w strefie docisku.

Zasady konstruowania zbrojenia na docisk.

Zbrojenie na docisk można kształtować w postaci siatek zgrzewanych z prętów prostych, siatek z prętów wyginanych (wężyków) l

ub uzwojenia. Przykłady przedstawia poniższy rysunek.

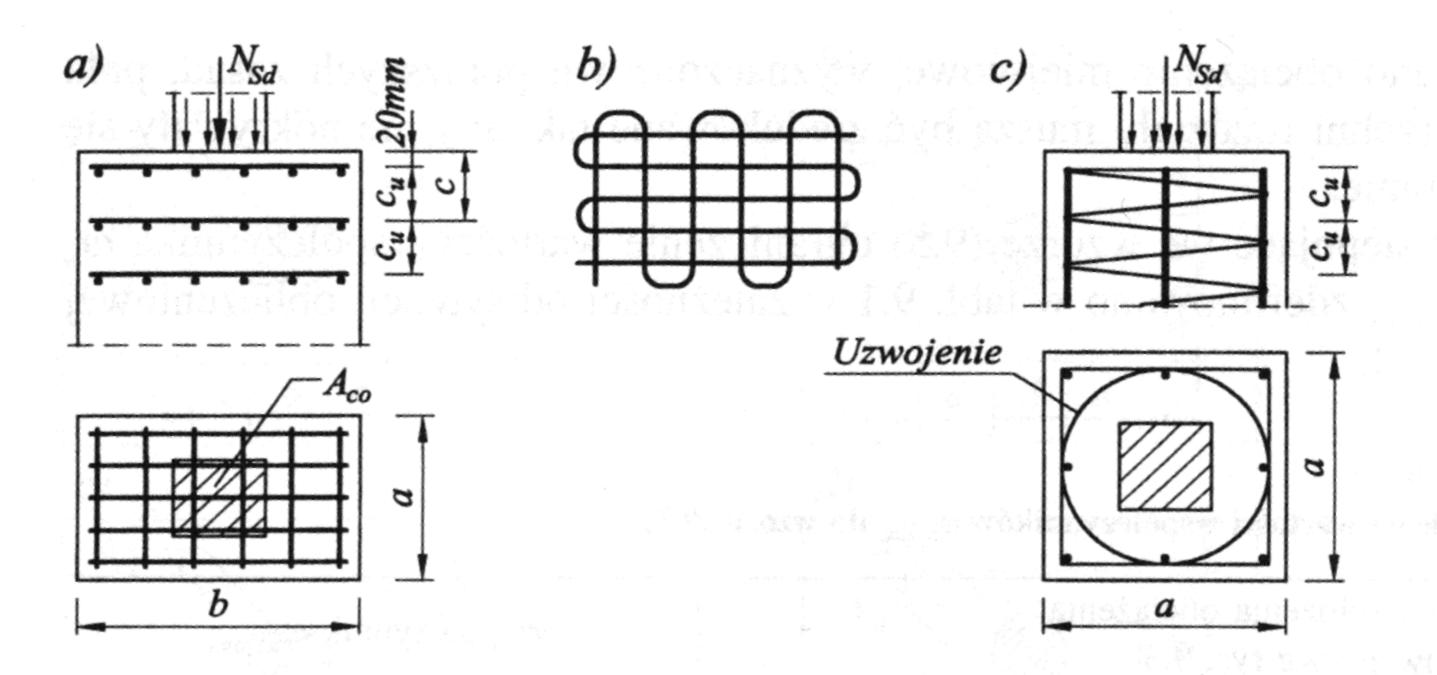
Płyty jednokierunkowo i krzyżowo zbrojone.

Płyty żelbetowe to płaskie elementy nośne obciążone w płaszczyźnie prostopadłej do swej powierzchni. Są stosowane w stropach budynków mieszkalnych i przemysłowych lub też występują jako części składowe zbiorników, ścian oporowych, fundamentów i schodów.

Ponadto stosunek rozpiętości l_eff płyty do wysokości użytecznej przekroju d nie powinien być większy niż:

40- w przypadku płyt wolno podpartych jednokierunkowo zbrojonych,

50 - w przypadku płyt zamocowanych i ciągłych jednokierunkowo oraz krzyżowo zbrojonych.

1. płyty jednokierunkowo zbrojone

Typowe schematy statyczne jednoprzęsłowych płyt jednokierunkowo zbrojonych przedstawia rys. 12.1.

Płyty ciągłe stosowane powszechnie w stropach płytowo - żebrowych i sztywno połączone na podporach z belkami, można traktować jako podparte przegubowo.

Obliczenia statyczne:

Obliczenia statyczne jednoprzęsłowych wolno podpartych lub wspornikowych należy przeprowadzać, zakładając sprężystą pracę ustroju. Płyty ciągłe można obliczać wg teorii sprężystości albo metodą plastycznego wyrównania momentów.

Jeżeli długości przęseł nie różną się między sobą o więcej niż 20 % to wartości momentów ekstremalnych w przęsłach i na podporach można określić na podstawie tablic Winklera. Należy zwrócić tu uwagę na odpowiednie ustawienie obciążeń zmiennych w celu uzyskania ekstremalnych wartości sił wewnętrznych.

Zasady obliczania i konstruowania zbrojenia.

Płyty jednokierunkowo zbrojone charakteryzuje nieskomplikowany układ zbrojenia głównego na zginanie. Zbrojenie to rozmieszcza się w kierunku efektywnej rozpiętości płyty l_eff , w strefach rozciągania jej przekrojów.

Dodatkowo w kierunku prostopadłym do l_eff układa się pręty rozdzielcze.

Mogą być one zbrojone prętami pojedynczymi lub siatkami z prętów zgrzewanych. W płytach monolitycznych średnica prętów powinna być nie mniejsza niż 4,5 mm, a siatek - niż 3 mm.

Maksymalny rozstaw prętów zbrojenia głównego w płytach jednokierunkowo zbrojonych o grubości h wynosi:

• przy h≤100 mm, s₁≤120 mm

• przy h>100 mm, s₁≤1,2 h oraz s₁≤250 mm

Do podpory należy doprowadzić bez odgięć nie mniej niż 1/3 dolnych prętów potrzebnych w przęśle i nie mniej niż 3 pręty na 1 m szerokości przekroju.

Jeżeli na podporze nie występują warunki zapewniające swobodę obrotu przekroju, należy zastosować odpowiednie zbrojenie górne.

Pręty rozdzielcze powinny mieć rozstaw nie większy niż 300 mm. Przejmują one naprężenia od skurczu , ułatwiają montaż i stabilizują układ zbrojenia głównego oraz przyczyniają siędo rozłożenia ewentualnego obciążenia skupionego na większą powierzchnię płyty.

Układ zbrojenia głównego w przekrojach podłużnych wynika z przebiegu momentów zginających.

Typowe rozwiązania dla płyt jednoprzęsłowych przedstawia poniższy rysunek.

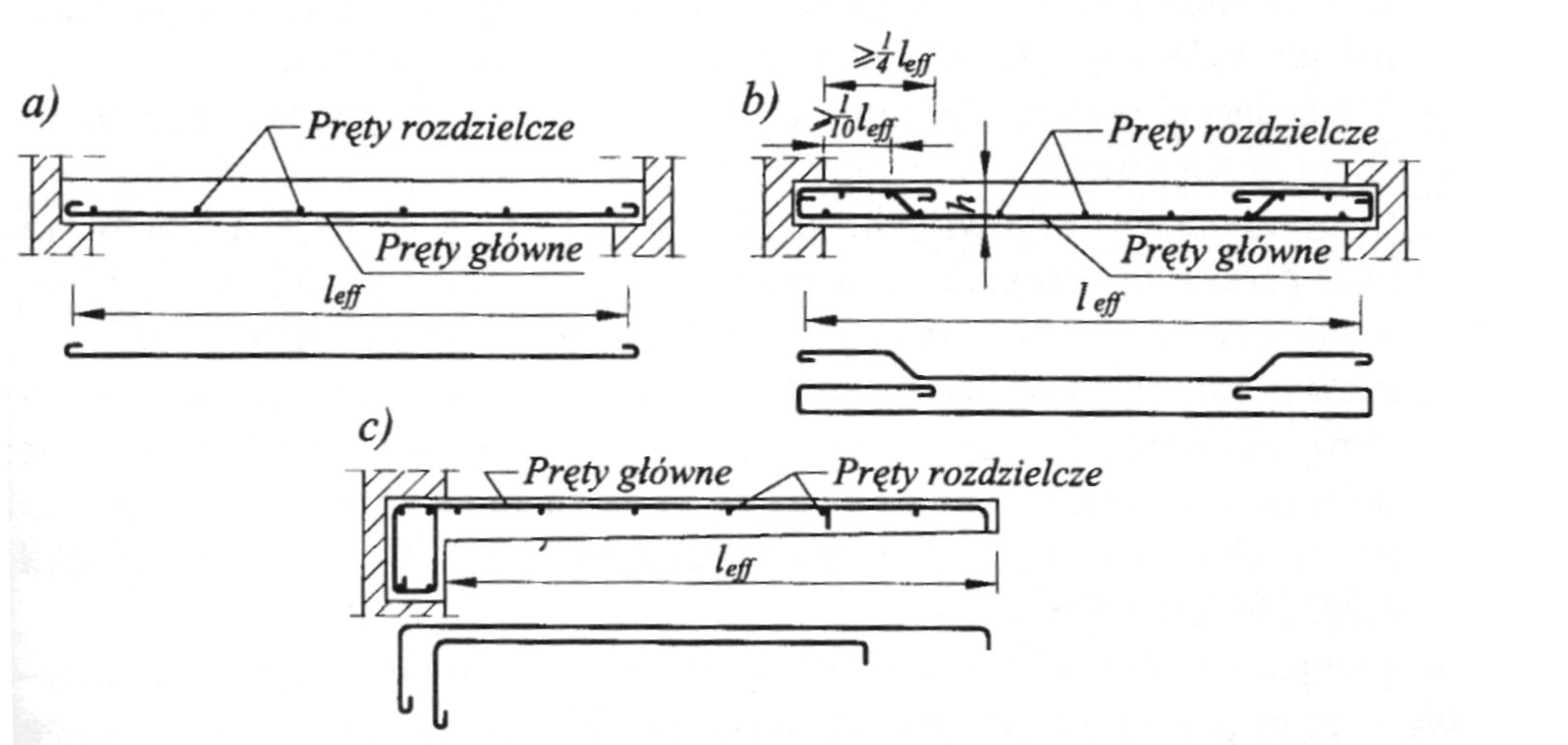
Przykładowe rozmieszczenie zbrojenia złożonego z ciągłych prostych oraz odgiętych prętów w płycie wieloprzęsłowej pokazuje rys. 12.6.

W przypadku otworów występujących w polu płyty, obrzeża otworów powinny być dodatkowo zbrojone.

Jeżeli wymiary otworu nie przekraczają 1/4 obliczeniowej rozpiętości płyty, zaś obliczeniowe obciążenie płyty ponad ciężar własny jest nie większe niż 10 kN/m², ,przekrój zbrojenia obrzeżnego powinien być nie mniejszy niż przekrój zbrojenia przypadającego na szerokość otworu. W przeciwnym wypadku należy zaprojektować wzmocnienie płyty w postaci wymianów. Szerokość wymianów, jako belek ukrytych nie może przekraczać 4 grubości płyty.

W płytach ze zbrojeniem głównym umieszczonym równolegle do podpory ( np. podciągu lub ściany) należy stosować dodatkowe zbrojenie górne, umieszczone prostopadle do tej podpory (rys. 12.7). Zbrojenie to ma przenosić naprężenia rozciągające, jakie powstają w wyniku zginania płyty prostopadle do kierunku jej pracy.

Nośność tego zbrojenia powinna być nie mniejsza niż 1/3 nośności zbrojenia głównego w płycie. Powinno też przenieść siłę o wartości 40 kN na każdy metr długości rozpatrywanej podpory.

Obliczone zbrojenie powinno być wpuszczone w płytę na szerokość nie mniejszą niż 1/4 jej rozpiętości po każdej stronie podpory. Jednocześnie pole zbrojenia głównego płyty w paśmie przylegającym do rozpatrywanej podpory może być zredukowane do połowy.

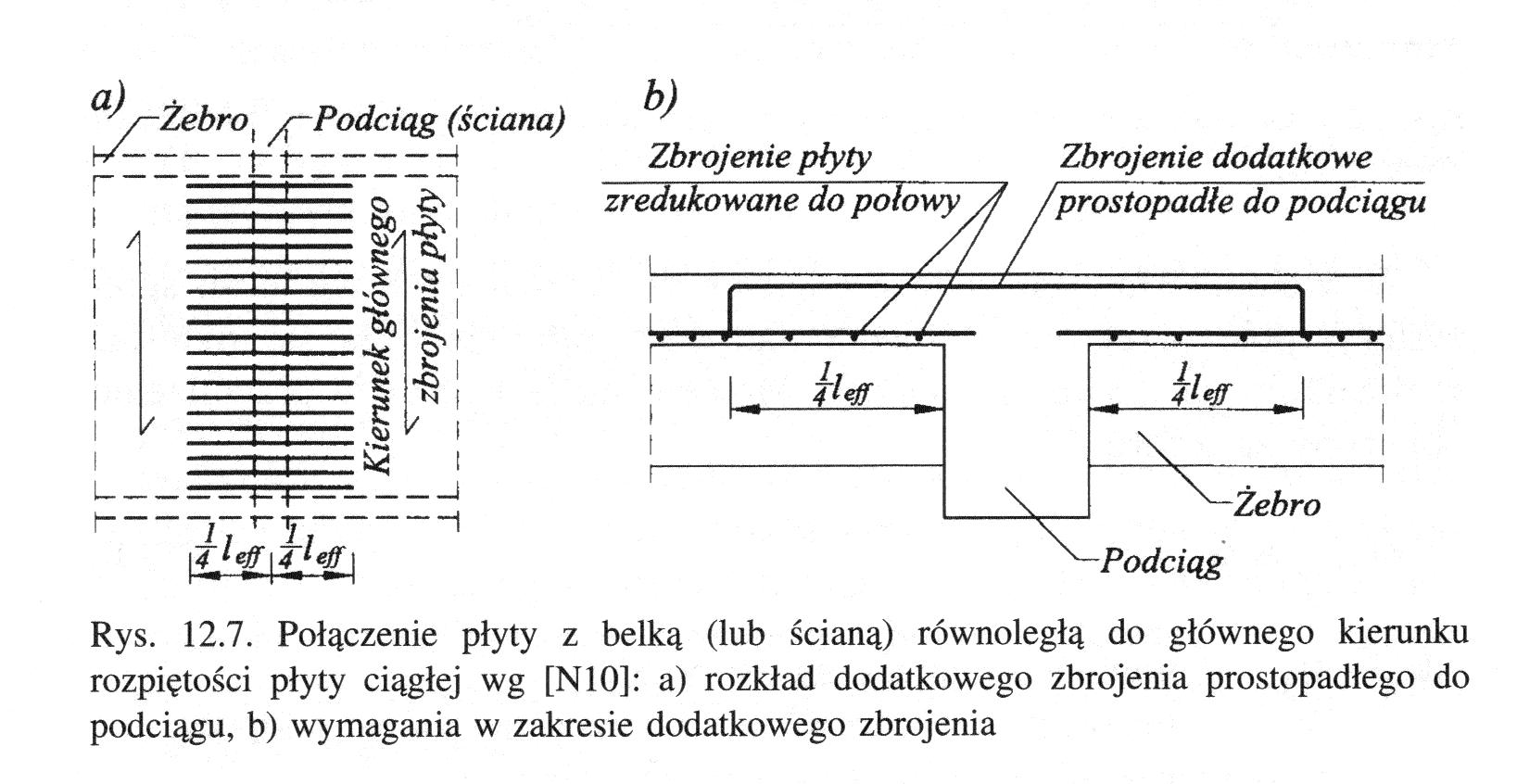
b) płyty krzyżowo (dwukierunkowo) zbrojone

Płyty spełniające warunek 0,5 ≤ l_y/l_x ≤ 2,0 , rozpatruje się jako zginane w dwóch płaszczyznach. Można je traktować jako ustroje jednopolowe, najczęściej jednak projektowane są jako wielopolowe. Typowe przykłady zastosowań to stropy płytowo-żebrowe, kasetonowe lub rusztowe.

Obliczenia statyczne:

Można je przeprowadzać wg teorii cienkich płyt sprężystych lub teorii nośności granicznej. Schematy statyczne jednopolowych płyt opartych na czterech krawędziach pokazano na rys. 12.8

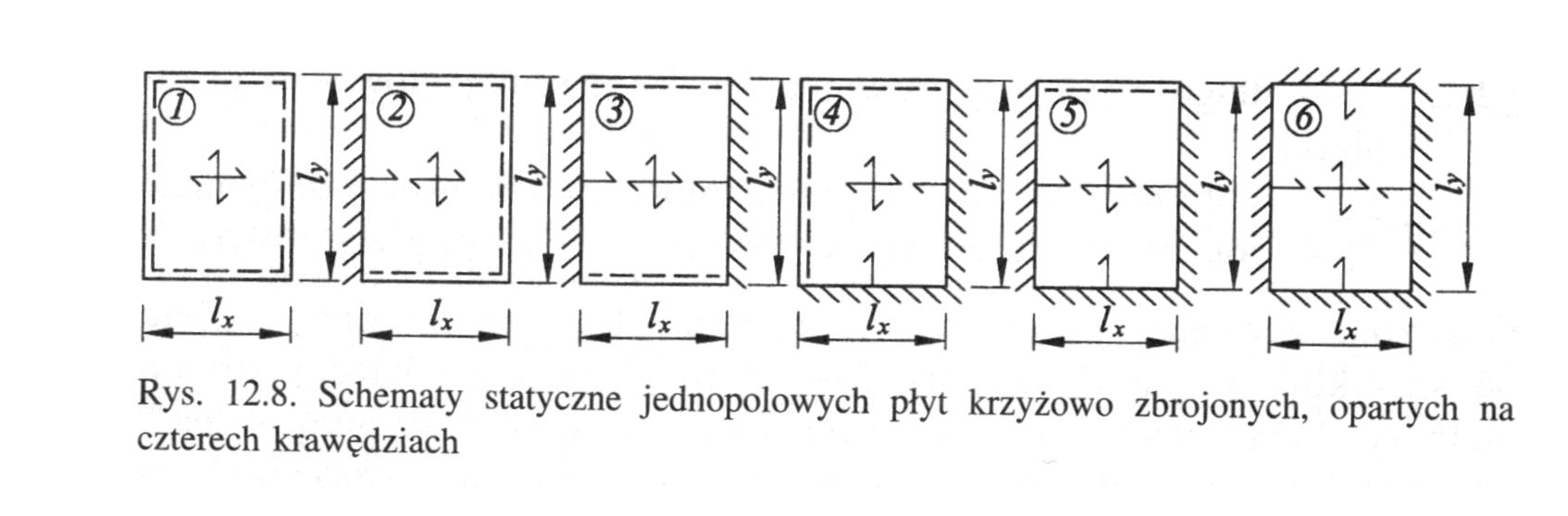
Momenty zginające w obu kierunkach można obliczać za pomocą tablic, jednak coraz szersze zastosowanie mają tutaj programy komputerowe wykorzystujące MES.

Zbrojenie płyt prostokątnych pracujących dwukierunkowo.

Wg PN-99 w jednoprzęsłowych płytach podpartych na czterech krawędziach, wymiarowanych zgodnie z teorią sprężystości, zbrojenie przęsłowe na zginanie każdego z kierunków x i y należy układać w strefie środkowej o wymiarach 3/5 l_x i 3/5 l_y. W pasmach skrajnych, poza wyznaczoną wyżej strefą środkową, przekrój zbrojenia może być zmniejszony do połowy. Maksymalny rozstaw prętów zbrojenia głównego w płytach krzyżowo zbrojonych o grubości h wynosi s₁ ≤ 250 mm.

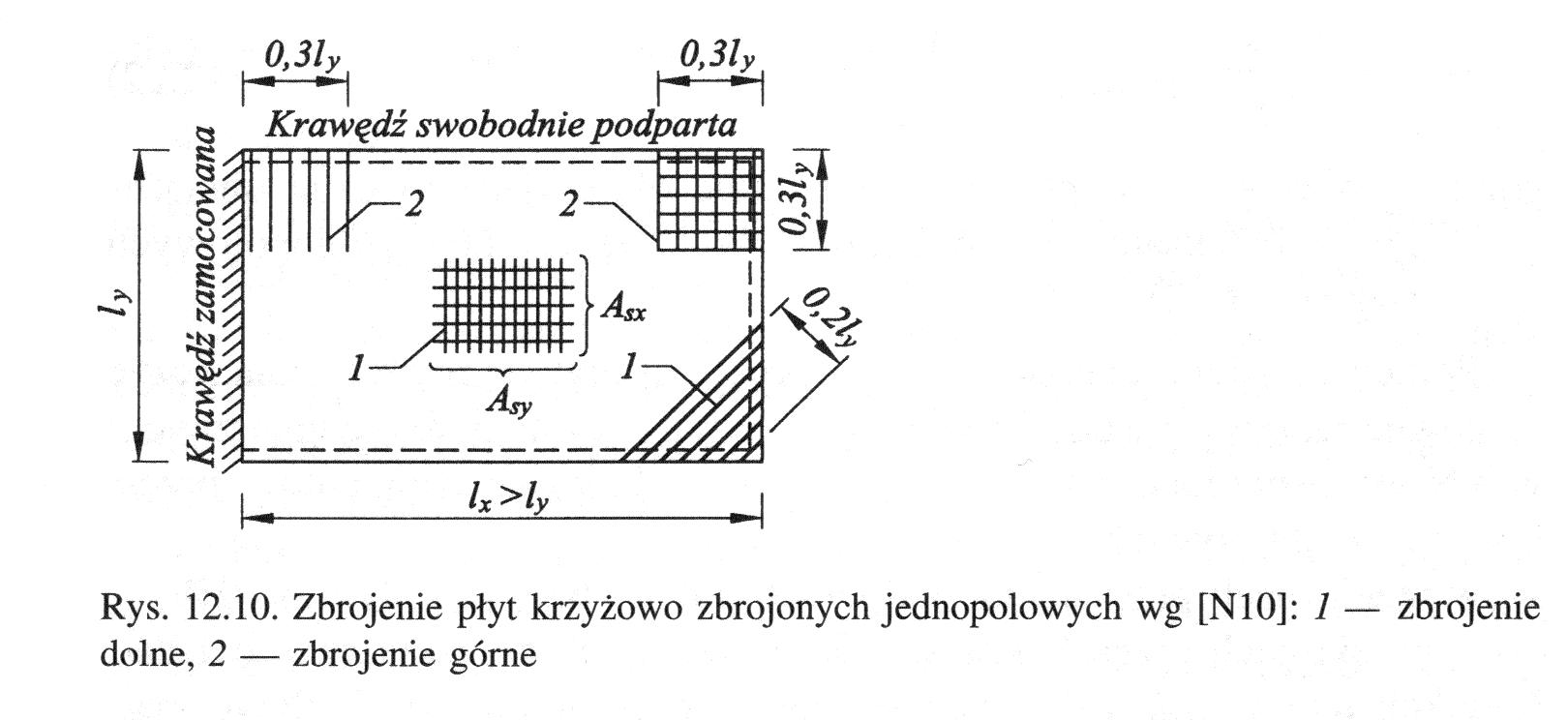
W narożach wolno podpartych należy umieszczać dwukierunkowe zbrojenie górne, równoległe do krawędzi, na szerokości równej 0,3 mniejszej rozpiętości (rys. 12.10). Przekrój tego zbrojenia na jednostkę szerokości płyty powinien wynosić w każdym kierunku co najmniej połowę przekroju większego zbrojenia znajdującego się w środku płyty. W narożach, w których zbiega się krawędź swobodnie podparta z krawędzią zamocowaną postanowienie to rozciąga się jedynie na zbrojenie naroża równoległe do krawędzi zamocowanej, natomiast przekrój zbrojenia prostopadłego do krawędzi zamocowanej wynika z obliczeń.

W narożach wolno podpartych należy również umieszczać dodatkowe zbrojenie dolne, układane prostopadle do dwusiecznej i rozmieszczone na szerokości równej 0,2 mniejszej rozpiętości płyty. Przekrój tego zbrojenia na

1 m szerokości przekroju powinien być co najmniej równy przekrojowi większego zbrojenia w środku płyty. Podczas projektowania zbrojenia na zginanie należy pamiętać, że w płytach krzyżowo zbrojonych zachodzi konieczność zróżnicowania wysokości użytecznej płyty w kierunkach x i y.

Żebra, podciągi i wsporniki.

a) żebra, podciągi

Zasadniczymi elementami układów płytowych i płytowo-żebrowych są: płyta, żebra czyli tzw. belki drugorzędne oraz podciągi zwane też belkami głównymi.

Rozplanowanie żeber i podciągów należy stropu monolitycznego należy tak przeprowadzić, aby przekroje płyty, żeber i podciągów były ekonomicznie uzasadnione.

Najbardziej racjonalne rozpiętości tych elementów są następujące:

• żebra: rozpiętość 5 do 7 m,

• podciągi: rozpiętość 5 do 8 m.

Belki żelbetowe wykonywane są jako monolityczne lub prefabrykowane. Kształty przekroju poprzecznego i podłużnego dostosowuje się do ich funkcji statycznej i do sposobu wykonania elementu. Najczęściej spotykane przekroje poprzeczne belek żelbetowych ukazuje rys. 12.12.

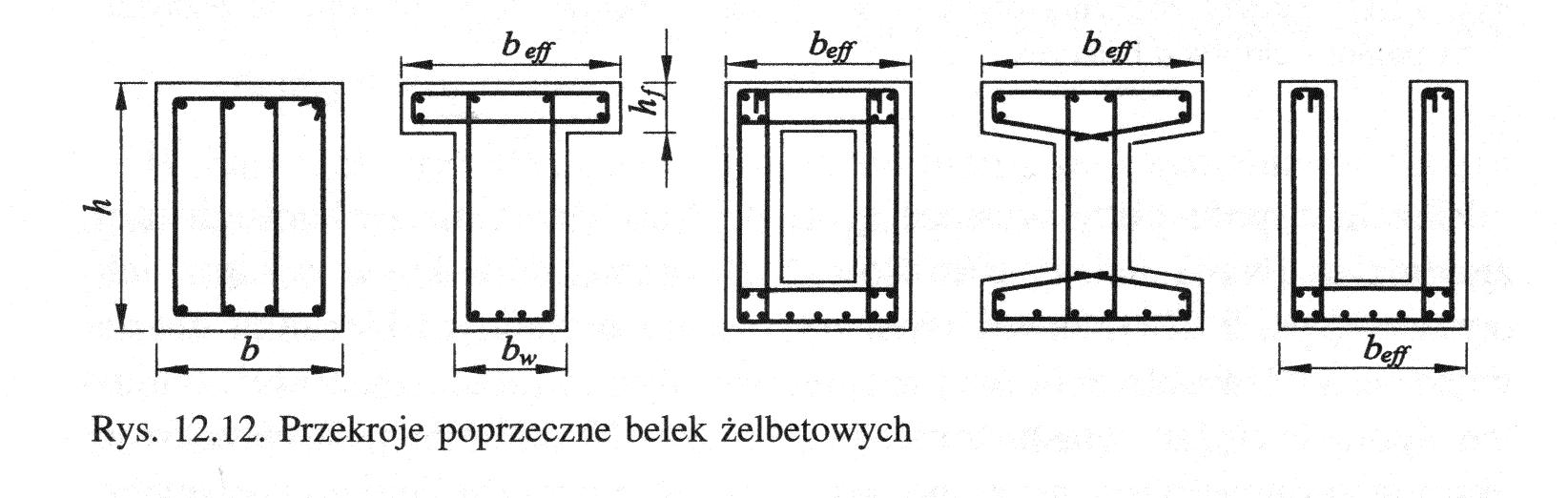
Wysokość podciągów przyjmuje się nie mniejszą niż 1/15 ich rozpiętości, a żeber 1/20 rozpiętości.

Szerokość belek o przekroju prostokątnym wynosi zwykle od 0,3 do 0,5 ich rozpiętości.

Obliczenia statyczne belek

Belki wieloprzęsłowe, sztywno połączone na podporach z innymi belkami lub słupami, można obliczać jako ustroje ciągłe podparte przegubowo. Siły wewnętrzne w belkach ciągłych o równej bądź zbliżonej rozpiętości przęseł można wyznaczać korzystając z tabli Winklera. Obecnie jednak najczęściej stosuje się programy komputerowe.

Zasady zbrojenia belek

W belkach wyróżnia się zbrojenie główne i pomocnicze. Zbrojenie główne to pręty podłużne zaprojektowane na zginanie oraz strzemiona lub pręty odgięte ze względu na ścinanie (i ewentualne skręcanie). Zbrojenie pomocnicze stanowią pręty montażowe oraz w niektórych przypadkach - przeciwskurczowe.

W belkach żelbetowych co najmniej 1/3 liczby prętów zbrojenia rozciąganego w przęśle, lecz nie mniej niż 2 pręty, należy doprowadzić do podpory bez odginania. W belkach żelbetowych i sprężonych w których dopuszcza się zarysowanie, jeżeli wysokość przekroju belki jest większa niż 700 mm, przy powierzchniach bocznych należy umieszczać podłużne pręty konstrukcyjne o średnicy nie mniejszej niż 8 mm w rozstawie nie większym niż 250 mm. Belki o wysokości przekroju większej niż 1000 mm, jak również belki zbrojone prętami o średnicy większej niż 25 mm powinny posiadać zbrojenie przypowierzchniowe.

Przykładowe zbrojenie belki jednoprzęsłowej (rys. 12.13)

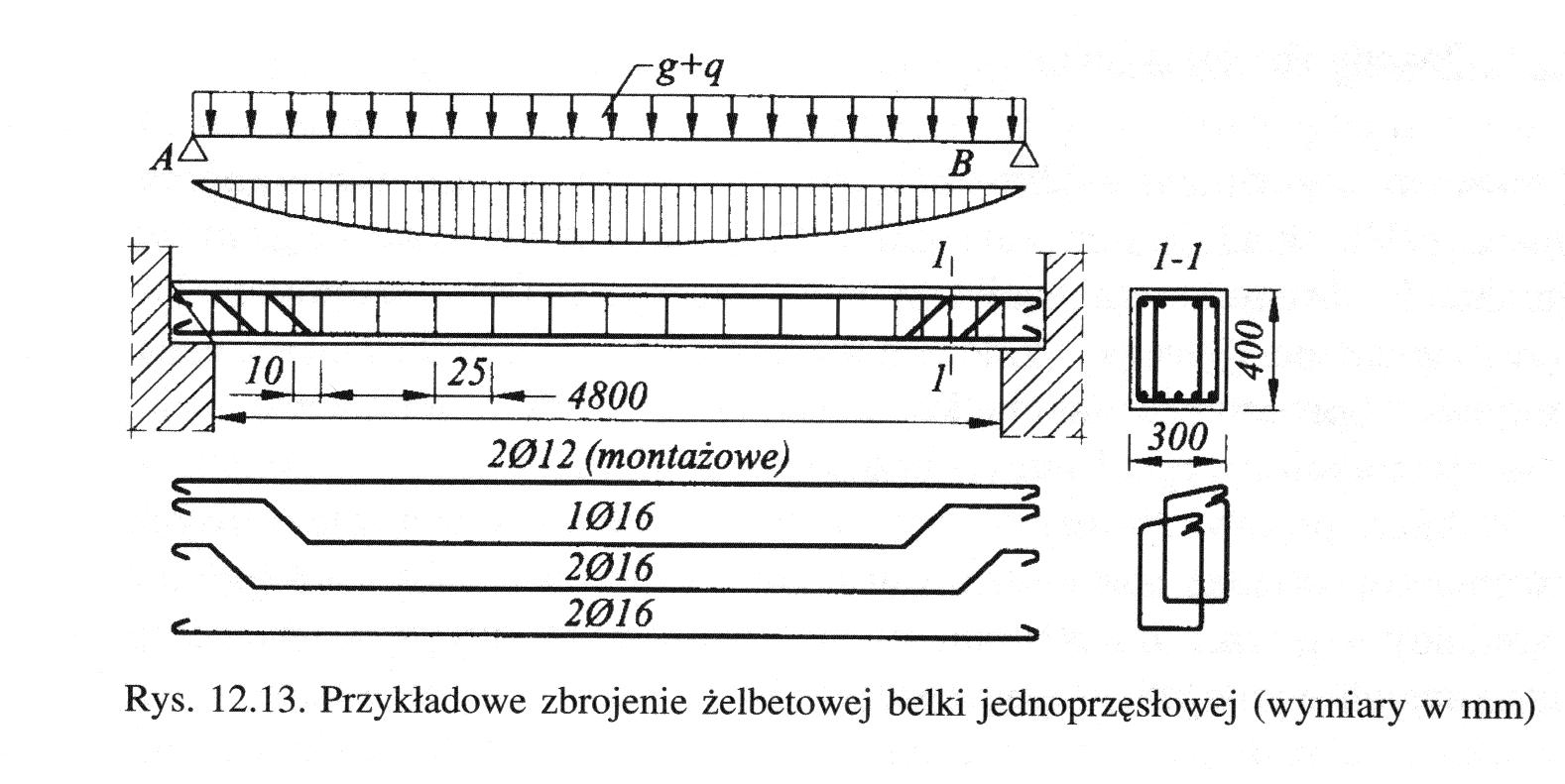
W belkach prostokątnych nie połączonych z płytami należy stosować strzemiona zamknięte. W belkach o szerokości większej niż 350 mm zbrojonych w strefie rozciąganej więcej niż 3 prętami należy stosować strzemiona czteroramienne.

W strefie ścinania zbrojonej strzemionami i prętami odgiętymi co najmniej 50 % obliczeniowej siły poprzecznej powinny przenosić strzemiona.

Połączenie żebra z podciągiem

Ze względów konstrukcyjnych takie połączenie powinno być zabezpieczone dodatkowym zbrojeniem, nie uwzględnianym w obliczeniach podciągu. Liczba strzemion zależy tu od wartości siły poprzecznej w podciągu w miejscu połączenia z belką drugorzędną. Jeżeli obliczeniowa siła poprzeczna w miejscu połączenia nie przekracza wartości:

V_Sd=2f_ctd b d

to należy stosować co najmniej 4 strzemiona jak to pokazano na poniższym rysunku.

Jeżeli siła poprzeczna jest większa to należy obliczyć przekrój strzemion korzystając ze wzoru normowego.

Jeżeli zbrojenie rozciągane żebra znajduje się poniżej podciągu (żebro podwieszone do podciągu), reakcję podporową belki w całości przejmują strzemiona o polu ΣA_sw , obejmujące pręty dolnego zbrojenia belki.

Do ΣA_sw można wliczać przekrój odgiętego zbrojenia głównego belki, pod warunkiem spełnienia wymagań w zakresie zagięcia i zakotwienia prętów.

2. wsporniki długie

wsporniki to elementy konstrukcyjne utwierdzone jednym końcem drugim zaś niepodparte. Mogą być wykonane jako płyty, belki, wykusze, dachy wspornikowe. Wsporniki pracują na moment ujemny.

Przykład zbrojenia płyty balkonowej przedstawia rys. 10.28

Obliczenie wsporników sprowadza się do znalezienia momentu utwierdzenia i siły poprzecznej. Mury w których utwierdza się wsporniki należy obliczać na ściskanie wywołane obciążeniem wspornika. Należy także sprawdzić wspornik na stateczność. Moment utrzymujący powinien być 1,5 razy większy od momentu obracającego.

3. krótkie wsporniki

Zadaniem krótkich wsporników, które z reguly są zamocowane w słupach, jest przenoszenie reakcji belek (rygli, belek podsuwnicowych w ustrojach ramowych monolitycznych lub prefabrykowanych.

Średnica prętów zbrojenia głównego krótkiego wspornika nie powinna być większa niż 25 mm. zaleca się stosowanie pętli poziomych i ukośnych.

---