Ad1 Równania Maxwella są podstawowymi równaniami elektromagnetyzmu . Równania te odgrywają w elektromagnetyzmie podobną rolę jak prawa Newtona w dynamice.

1 równanie Maxwella - prawo Faradaya dla indukcji elektromagnetycznej mówi że zmienne pole magnetyczne wytwarza wirowe pole elektryczne, które może wywoływać prąd elektryczny. Z I równania Maxwella wynika też, że gry brak pola magnetycznego, bądź też pole magnetyczne jest stałe, to istniejące pole elektryczne jest bezwirowe. Takie pole to pole elektrostatyczne wywoływane przez stacjonarne ładunki elektryczne.

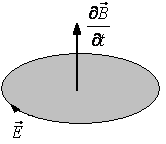
2 równanie Maxwella - uogólnione prawo Ampere'a mówi, że prąd elektryczny lub zmienne pole elektryczne wytwarza wirowe pole magnetyczne.

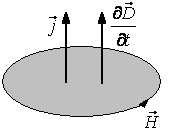
3 równanie Maxwella - prawo Gaussa dla pola elektrycznego mówi, że źródłami pola elektrycznego są ładunki. Jeżeli brak jest ładunków elektrycznych to linie pola elektrycznego są liniami zamkniętymi.

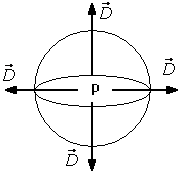
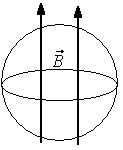
4 równanie Maxwella - prawo Gaussa dla pola magnetycznego mówi, że nie istnieją w przyrodzie ładunki magnetyczne. Linie indukcji pola magnetycznego są liniami zamkniętymi.

Ad3. Polaryzacja światła. Metody polaryzacji światła spolaryzowanego.

Światłem spolaryzowanym nazywa się światło, w którym drgania wektora świetlnego są w jakiś sposób uporządkowane. Światło naturalne można przedstawić jako nałożenie się dwóch niespójnych fal elektromagnetycznych spolaryzowanych w płaszczyznach wzajemnie prostopadłych i mających jednakowe natężenie. Dwie spójne płasko spolaryzowane fale świetlne, w których płaszczyzny drgań są wzajemnie prostopadłe dają w wyniku nałożenia falę świetlną spolaryzowaną eliptycznie. Dla różnicy faz
równej zeru lub
elipsa redukuje się do prostej i powstaje światło spolaryzowane liniowo. Dla
=
lub
= -
i jednoczesnej równowadze amplitud drgań składowych elipsa przechodzi w okrąg koła - światło spolaryzowane kołowo.

Metody polaryzacji światła :

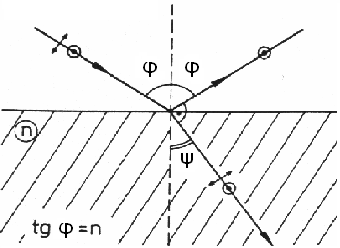
Polaryzacja przez odbicie i załamanie - Jeżeli kąt padania światła niespolaryzowanego padającego na granicę dwóch dielektryków nie jest równy zeru, to wiazka odbita jest częściowo spolaryzowana. Stwierdzono że dla szkła (oraz innych dielektryków) istnieje pewien kąt padania φ który nosi nazwę kąta całkowitej polaryzacji lub kąta Brewstera dla którego wiązka odbita jest całkowicie spolaryzowana. W wiązce całkowicie spolaryzowanej odbija się tylko składowa prostopadła wektora elektrycznego fali świetlnej, natomiast jego składowa równoległa do płaszczyzny padania nie ulega odbiciu. Jeżeli kąt padania α jest równy kątowi φ to wiązki odbita i załamana tworzą kąt prosty: φ+ψ=90 podstawiając ten związek do równania Sneliusa:

Polaryzacja przez podwójne załamanie:

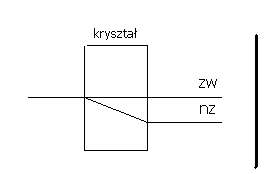
Zjawisko polega na tym ze padający na kryształ promień rozdziela się wewnątrz kryształu na dwa promienie : promień niezłamany (zw) nosi nazwę promienia zwyczajnego a promień załamany(nz) nosi nazwę promienia nadzwyczajnego. Podwójnym załamaniem nazywamy zatem zjawisko polegające na tym że przy przechodzeniu światła przez pewne ośrodki promień padający rozszczepia się na dwa promienie: zwyczajny i nadzwyczajny, promienie te są spolaryzowane liniowo w płaszczyznach wzajemnie prostopadłych.

Ad4 Prawo Malusa. Ćwierćfalówka

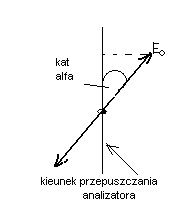
Zależność opisana równaniem I=b(E₀)³cos² α ,gdzie I₀=b(E₀ )² to natężenie wiązki padającej, b- stała i I=bE² to natężenie wiązki światła po przejściu przez analizator stanowi najprostszą postać prawa Malusa z 1808r.Jest to szczególny przypadek znanego obecnie ogólnego prawa Malusa. W rzeczywistym analizatorze występuje niedoskonała polaryzacja, odbicie pochłanianie światła, a ponadto wiązka światła padającego nie musi być spolaryzowana zupełnie i liniowo.

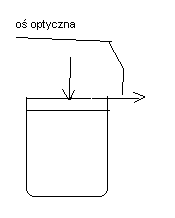
Ćwierćfalówka : płytka opóźniająca. Najmniejsza grubość płytki polaryzującej kołowo δ=π/2 wynosi
Ćwierćfalówka daje różnicę dróg optycznych obu promieni - równą ¼ długości fali światła padającego. Ćwierćfalówka zmienia polaryzację liniową na eliptyczną (i odwrotnie)

ΔΦ₀=2Π/λ₀·l·n₀ -promienie zwyczajne

ΔΦ_e=2Π/λ₀·l·n_ec - promienie nadzwyczajne

ΔΦ=2Π/λ₀·l·(n_o - n_e)

Jeżeli ΔΦ=Π/2 , to Π/2=2Π/λ₀·l·(n_o - n_e)

Stad wynika: l= λ₀ /4·(n_o - n_e)

Ad5 Dwójłomność wymuszona. Skręcanie płaszczyzny polaryzacji.

Dwójłomność spowodowana czynnikiem zewnętrznym nazywa się dwójłomnością wymuszoną lub indukowaną. Zjawisko dwójłomności wymuszonej wywołują naprężenia mechaniczne, odkształcenia, pole elektryczne, pole magnetyczne oraz gradient temp. Jeżeli te czynniki działają na ośrodek naturalnie dwójłomny, to dwójłomność tego ośrodka zmienia się.

Wiązka światła biegnąc w ośrodku dwójłomnym rozdziela się na dwie wiązki spolaryzowane w kierunkach wzajemnie prostopadłych .Wiązki te poruszają się różnymi prędkościami fazowymi. Związaną z tymi prędkościami różnicę współczynników załamania nazywamy dwójłomnością

Δn: Δn=n_w-n_s,

n_w-współczynnik załamania wiązki wolniejszej

n_s-współczynnik załamania wiązki szybszej.

Zmiana dwójłomności wywołana zewnętrznym polem elektrycznym jest nazywana zjawiskiem elektrooptycznym. Przykładem dwójłomności wymuszonej mechanicznie może być ściskanie lub rozciąganie ciała. W badanym ciele powstaje wówczas promień zwyczajny i nadzwyczajny. które biegną z różnymi prędkościami tak, ze po wyjściu z ciała wystąpi między nimi różnica faz wskutek czego wytworzą one falę spolaryzowaną eliptycznie. Różnica promienia n_zw i n_nz jest proporcjonalna do iloczynu ciśnienia (naprężenia) p i stałej k zależnej od rodzaju ciała i długości fali światła. n_zw - n_nz =kp. Dwółomność taką ma np.szybko chłodzone szkło.

Dwójłomność powstała pod wpływem pola elektrycznego nosi nazwę zjawiska Kerra. Zjawisko to obserwuje się zarówno w ciałach stałych, gazach i cieczach a różnica współczynników załamania n_zw - n_nz jest proporcjonalna do kwadratu natężenia pola elektrycznego E czyli n_zw - n_nz =BE² , gdzie B to stała zależna od rodzaju cieczy.

Skręcanie płaszczyzny polaryzacji: Dwie spójne płasko polaryzowane fale świetlne, których płaszczyzny drgań są wzajemnie prostopadłe dają w wyniku nałożenia falę świetlna spolaryzowana eliptycznie. Dla różnicy faz δ równej zeru lub П elipsa redukuje się do prostej i powstaje światło spolar. Liniowo. Dla δ=+ П/2, - П/2 i jednoczesnej równości amplitud drgań składowych przechodzi w okrąg i powstaje światło spolar. Kołowo.

Ad6 Interferencja światłą. Prążki interferencyjne.

Interferencja światła - fale o jednakowych długościach wzmacniają się najsilniej jeżeli różnica ich dróg optycznych jest równa wielokrotności długości fali a maksymalnie się osłabiają jeżeli różnica ich dróg optycznych jest wielokrotnością połówek długości fali.

Prążki interferencyjne są wytwarzane przy użyciu warstwy powietrza o zmiennej grubości

Powstającej pomiędzy soczewka wypukła o dużym promieniu krzywizny a płytka płasko- równoległa na której ta soczewka leży.

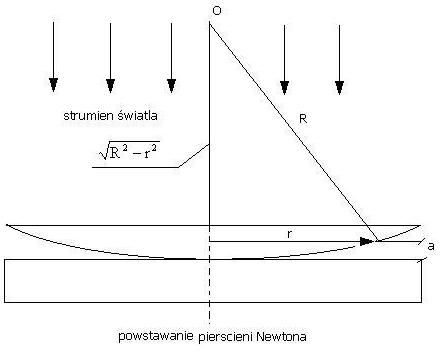
Promienie światła padające pod bardzo małym katem na plaska powierzchnie soczewki ulegają odbiciu na jej przedniej i tylniej ściance oraz na powierzchni płytki płasko -równoległej. Prążki powstają wskutek interferencji promieni odbitych od dolnej (zakrzywionej) powierzchni soczewki z promieniami odbitymi od górnej powierzchni płytki płasko-równoległej.

Ad7 Doświadczenie Younga- Thomas Young wykazał doświadczalnie, że światło jest falą, co było sprzeczne z poglądami większości uczonych ówczesnych. Dowód Younga polegał na wykazaniu, że światło może interferować, tak jak interferują fale wodne, fale dźwiękowe i wszystkie fale innych rodzajów. Eksperyment polega na przepuszczeniu światła poprzez dwa pobliskie otwory w przesłaniu i rzutowaniu na ekran. Na ekranie wskutek interferencji tworzą się charakterystyczne prążki potwierdzające falową naturę światła. Aby wykonać doświadczenie należy użyć siatki dyfrakcyjnej, czyli płytki szkła, na której gęsto zarysowane są rysy.

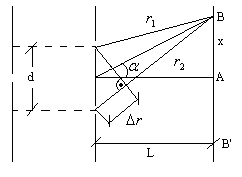
Można wyznaczyć długość fali :

- prążek jasny

- prążek ciemny

Ad8 Koherencja światła. Wpływ koherencji czasowej i przestrzennej na prążki w doświadczeniu Younga

Płaska falę elektromagnetyczna, rozchodzącą się z na przykład wzdłuż osi x można opisać równaniamiα

E=E₀sin(ωt-kx+α)

H=H₀ sin(ωt-kx+α)

Gdzie E ₀ to amplituda wektora pola elektrycznego, H₀ to amplituda wektora pola magnetycznego, ω-pulsacja,α-faza początkowa, k- liczba falowa. Działania takie jak fotoelektryczne, fotochemiczne, fizjologiczne są wywołane głownie drganiami wektora elektrycznego(świetlnego).Wyżej zapisane równania pokazują prawo według którego zmienia się w czasie i przestrzeni wektor świetlny, jego moduł opisuje równanie

E=E₀sin(ωt-kx+α), które nazywamy równaniem fali świetlnej, a wielkość E ₀ amplitudą fali świetlnej.

Dla dwóch fal o jednakowej pulsacji ω, poruszających się w tym samym kierunku.

E`=E₁sin(ωt-kx+α)

E`=E₁sin(ωt-kx+α) ,amplituda fali wypadkowej, powstałej w wyniku nałożenia się fal wyrazi się równaniem K² =(K₁)² +(K₂)²+2K₁·K₂cos(α₂ -α₁), jeżeli różnica faz (α₂ -α₁ )będzie stała, to amplituda wypadkowej fali świetlnej jest stała w czasie.Fale takie nazywamy koherentnymi lub spojnymi.Dodając amplitudy fal świetlnych spójnych możemy obliczyć natężenie fali wypadkowej. I =I₁ +I₂+2 (I₁· I₂)^1/2 cos(α₂ -α₁), po obliczeniu natężeń fal składowych otrzymamy natężenie fali wypadkowej I =I₁ +I_2, w punktach przestrzeni, w których cos(α₂ -α₁)>0, natężenie I >I₁ +I_2, w innych miejscach przestrzeni w których cos(α₂ -α₁)<0 nateżenie wypadkowej I <I₁ +I_2. Przy nakładaniu się na siebie fal swiatła spójnego powstają w pewnych punktach przestrzeni minima i maksima.Jest to interferencja światła, gdy I ₁=I₂ =I₀ natężenia fal świetlnych są jednakowe i równanie przyjmuje postać; I =2I₀ [(1+ cos(α₂ -α₁)]. Jeżeli na ekran padają dwie wiązki światła spójnego o jednakowym natężeniu to powstanie na nim obraz interferencyjny, w którym natężenie prążków będzie opisane wyzej zapisanym równaniem. a)schemat interferencji dwóch wiązek światła spójnego, b)obraz interferencyjny

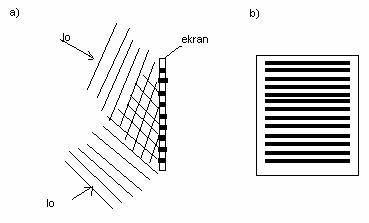
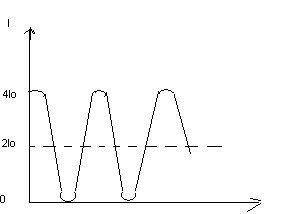
Przebieg natężenia fali wypadkowej powstałej w wyniku nałożenia się dwóch spójnych fal o jednakowym natężeniu w zależności od różnicy faz

Ad9 Interferencja równej grubości - Zazwyczaj zakłada się, że warstwa ośrodka o współczynniku załamania n i grubości h jest płasko-równoległe, a rozbieżność wiązki równa zeru. Oba te warunki są niemożliwe do ścisłego spełnienia. Zarówno grubość warstwy jak i kąt padania promieni mogą się zmienić. Jeżeli mierzona jest grubość, a kąt padania jest w wystarczającym stopniu stały, obserwujemy jasne prążki w miejscach, w których grubość spełnia warunek: wzór:

k - liczba całkowita

n - współczynnik załamania

α₁ - kąt padania

Nazywamy je prążkami równej grubości. Odmianą prążków równej grubości są pierścienie Newtona.

Ad10 Interferencja równego nachylenia - Zazwyczaj zakłada, żę warstwa ośrodka o współczynniku załamania n i grubości h jest płaskorównoległa, a rozbieżność wiązki równa zeru. Oba te warunki są niemożliwe do spełnienia. Zarówno grubość warstwy jak i kąt padania mogą się zmieniać. Jeżeli mamy stałą grubość to obserwujemy prążki równego nachylenia dla promieni o kątach padania α_k które znaleźć ze wzoru:

k - liczba całkowita

n - współczynnik załamania

h - grubość

Przykładem mogą być barwy interferencyjne baniek mydlanych.

Ad12 Dyfrakcja typu Fraunhofera

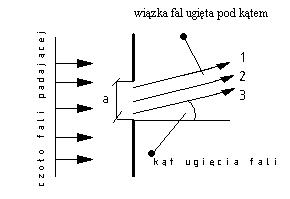
Dyfrakcja (ugięcie) fali na pojedynczej szczelinie. Szczelinę o skończonej szerokości a , na którą pada płaska monochromatyczna fala, zgodnie z zasadą Huygensa, możemy traktować jak zbiór nieskończonej ilości źródeł drgających zgodnie w fazie. Dyfrakcją fali na pojedynczej szczelinie nazywamy interferencję fal od tej nieskończonej ilości źródeł rozłożonych na jej powierzchni.

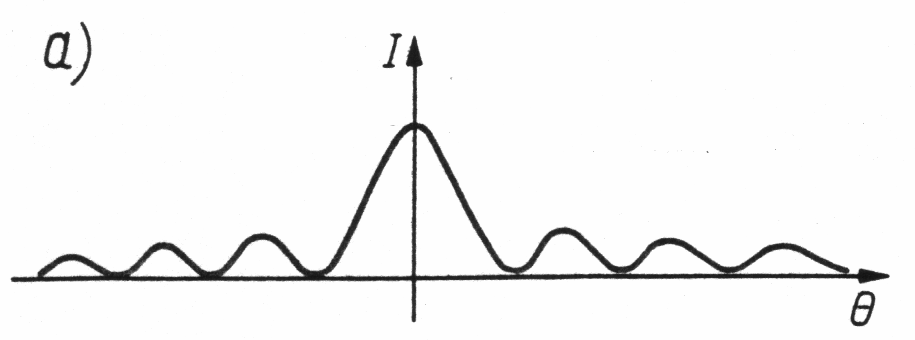
1. Obraz dyfrakcyjny jest zawsze symetryczny

2. W środku obrazu dyfrakcyjnego natężenie światła osiąga max

Natężenie światła za szczeliną:
I - natężenie fali ugiętej pod kątem

I_o - max natężenie fali

gdzie:

Ad13 Dyfrakcja Frensela

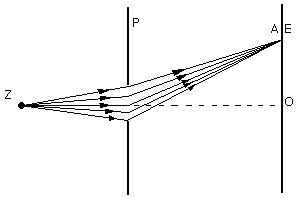
Dyfrakcja światła na szczelinie. Zjawisko dyfrakcji światła polegające na uginaniu się promieni świetlnych napotykających na swej drodze przeszkody w wyniku czego występują odstępstwa od prostoliniowego ich biegu jest ściśle związane z falową naturą światła.

Na rysunku pokazano ugięcie promieni świetlnych, wychodzących ze źródła światła Z na brzegach wąskiej szczeliny w przesłonie P. Promienie ugięte padają na punkt A na ekranie E tworząc na nim obraz źródła światła Z. Gdy źródło światła Z i ekran E na którym pojawia się obraz znajdują się w malej odległości ugięcie to nosi nazwę Fresnela.

Ad14 Chromatyczna zdolność rozdzielcza i dyspersja siatki dyfrakcyjnej dwupunktowa zdolność rozdzielcza, kryterium Rayleigha

Siatką dyfrakcyjną nazywamy zbiór dużej liczby jednakowych, równoległych szczelin, między którymi występują równe odstępy. Podstawowymi wielkościami charakteryzującymi siatkę dyfrakcyjną są dyspersja i zdolność rozdzielcza. Dyspersja określa kątową lub liniową odl. Między dwiema liniami widzialnymi, różniącymi się długością fali o jedną jednostkę .Dyspersja kątowa: D=dφ/dλ=m/dcosφ, D≈m/d - przy dużych kątach cosφ≈1. Dyspersja liniowa: Dlim=f `m/d, gdzie f-ogniskowa soczewki skupiająca na ekranie promienie ugięte.

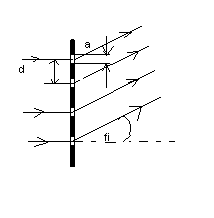
Zdolność rozdzielcza: Możliwość odróżnienia dwóch maksimów obrazu dyfrakcyjnego zależy nie tylko od odległ. między nimi ale również od ich szerokości. W celu rozróżnienia dwóch leżących obok siebie maksimów(plamek świetlnych lub linii) stosujemy kryterium Rayleigh, które mówi, że: Obrazy dwóch leżących blisko siebie oddzielonych punktów świecących można uważać jeszcze za rozdzielone, jeżeli środek głównego maksimum dyfrakcyjnego jednego z nich leży w pierwszym minimum dyfrakcyjnego drugiego. Zdolność rozdzielcza siatki dyfrakcyjnej jest proporcjonalna do rzędu widma m i całkowitej liczbie szczelin(nacięć) N siatki. R=mN

Siatka dyfrakcyjna szczelinowa pokazana na rysunku o szerokości szczelin a i stałą siatki d (odległością miedzy sąsiednimi szczelinami).Miedzy promieniami padającymi a ugiętym powstaje kąt określony stosunkiem λ/d, a względne natężenie tych prążków zależy od stosunku λ/a. Różnica dróg optycznych promieni wychodzących z dwóch sąsiednich szczelin wynosi dsinφ, gdzie φ-kąt ugięcia. Wzmocnienie (maksima główne) natężenia powstanie gdy spełniony zostanie warunek dsinφ=mλ, gdzie m=1,2,3…to rzędy widma. Dla a=Nd otrzymujemy warunek na położenie minimów natężenia dsinφ=kλ/N, gdzie k=1,2,3…Dla k=N otrzymujemy pierwsze maksimum główne(m=1).W miarę zwiększania liczby szczelin siatki N maksima główne stają się coraz węższe, a maksima wtórne coraz mniejsze.

Funkcja falowa Ψ.Zgodnie z hipotezą de Broglie'a,w mikroświecie,cząstki takie jak elektron czy proton,mają własności falowe.Własności falowe cząstki (lub innego obiektu)w mechanice kwantowej opisuje tzw.funkcja falowa Ψ.Jest to w ogólnym przypadku zespolona funkcja współrzędnych przestrzennych oraz czasu Ψ (x,y,z,t).Funkcja falowa niesie w sobie wszystkie informacje o obiekcie (np.cząstce).Funkcja falowa musi być funkcją ciągłą,a także musi mieć ciągłą pochodną.Sens fizyczny ma kwadrat modułu funkcji falowej Ψ * Ψ =| Ψ |². Wielkość ∆P=| Ψ |² ∆V, gdzie ∆V jest małą objętością w przestrzeni,jest równa prawdopodobieństwu znalezienia cząstki w chwili t w objętości ∆V .Kwadrat modułu funkcji falowej | Ψ |²=∆P/∆V nazywamy gęstością prawdopodobieństwa znalezienia cząstki w chwili t w pewnym punkcie przestrzeni,w otoczeniu którego wybrano element objętości ∆V.

Rysunek przedstawia kwadrat modułu funkcji falowej cząstki przemieszczającej się w kierunku osi OX.Ma ona kształt krzywej dzwonowej,która z upływem czasu przesuwa się w kierunku osi OX (ruch cząstki) i jednocześnie rozmywa się.Po dostatecznie długim okresie czasu rozmycie to jest całkowite,tak że gęstość prawdopodobieństwa znalezienia cząstki w dowolnym miejscu przestrzeni będzie stała.Więc można powtórzyć jeszcze raz że cząstka z początku zlokalizowana w pewnym obszarze przestrzeni(krzywa dzwonowa) w przypadku braku oddziaływań staje się cząstką swobodną dla której | Ψ |² =const.

^{kwadrat modułu funkcji falowej} | Ψ |² =A²

,

-funkcja falowa cząstki swobodnej,

Energia cząstki swobodnej

Normowanie funkcji falowej.Prawdopodobieństwo znalezienia cząstki w przediale(x,x+∆x)

Warunek na funkcje falową:

Geometrycznie wartość powyższej całki równa jest całkowitemu polu pod krzywą dzwonową.Warunek powuższy nosi nazwę warunku normalizacji,a funkcję Ψ spełniającą ten warunek funkcją unormowaną.W przypadku trójwymiarowym warunek ma postać :

Aby funkcja falowa dała się uformować musi być ona również funkcją skończoną.Równanie Schroedingera.Funkcje falową Ψ dla danej cząstki,lub bardziej złożonego układu fizycznego,otrzymujemy rozwiązując równanie różniczkowe nazywane równanie Schroedingera

gdzie: U-energia potencjalna cząstki zależna od jej położeni, E-energia całkowita cząstki, Ψ-funkcja falowa spełniająca równanie Schroedingera, ∆-operator Laplace'a:

Jeżeli energia potencjalna cząstki U nie zależy od czasu,to równanie Schoedingera jest równaniem niezależnym od czasu i nazywa się stacjonarnym równaniem Schroedingera.Rozwiązanie tego równania jest możliwe tylko dla pewnych wartości energii E , które nazywamy dozwolonymi energiami układu,gdyż tylko takie wartości energii może dany układ fizyczny posiadać.Rozwiązując rów.Schroedingera dla dozwolonych wartości energi E ,otrzymujemy funkcje falowe Ψ(x,y,z)opisujące stany o tych energiach(stany stacjonarne).Stacjonarne rów.Schroedingera jest równaniem na wartości własne operatora energi całkowitej(tzw.operatora Hamiltona):

gdzie:H-operaator energii całkowitej,m-masa cząstki,∆-operator Laplace'a,U-energia potencjalna

Model Bohra atomu wodoru.Wzór na energie E_n elektronu w atomie wodoru,które otrzymuje się rozwiązując równanie Schroedingera,można otrzymać również stosując tzw.model Bobra.Model Bobra atomu wodoru opisuje atom wodoru jako układ,w którym elektron krąży wokół jądra atomu (protonu)po orbitach kołowych.Nie wszystkie orbity kołowe są dozwolone a tylko takie,dające się ponumerować liczbą naturalną n,na których elektron ma moment pędu o wartości będącej wielokrotnością stałej ħ: mr_n v_n =nħ.gdzie: r_n-jest promieniem dozwolonej orbity kołowej a v_n prędkością elektronu na tej orbicie.Numer orbity n można utożsamiać z główną liczbą kwantową.Model Bobra atomu wodoru został wyprowadzony przed powstaniem równania Schroedingera. Daje on prawidłowe wartości energii elektronu i długości emitowanej fali,nic nie mówi jednak o innych liczbach kwantowych,od których zależy stan elektronu.

Liczby kwantowe.Każda funkcja falowa opisuje nam jeden dozwolony stan elektronu.Ilość stanów elektronu równa jest ilości róznych funkcji falowych otrzymanych z rozwiązania równania Schroedingera.Funkcje falowe elektronu w atomie wodoru dadzą się ponumerować przy pomocy trzech liczb całkowitych n, l i m_l zwanych liczbami kwantowymi.(Istnieje jeszcze związana ze spinem czwarta liczba kwantowa .Magnetyczna spinowa liczba kwantowa m_s która wynosi ±0,5). Funkcja radialna R(r) zależy od n i l a funkcja kątowa Y(α,φ) od l i m_l. Przykłady funkcji kątowych:

Związek pomiędzy współrzędnymi r,α,φ a współrzędnymi kartezjańskimi x,y,z.

Energia elektronu w atomie wodoru E_n zależy jedynie od głównej liczby kwantowej n (n=1,2,3…n-1).Elektron posiadający określoną energię może znajdować się w różnych stanach opisanych liczbami kwantowymi l i m_l .Stany o różnych wartościach orbitalnej (azymutowej bądź też pobocznej) liczby kwantowej l (l=0,1,2…n-1),różnią się wartością orbitalnego momentu pędu.Stany dla l=0 nazywają się stanami s,stany dla l=1 stanami p,stany dla l=2 stanami d,następnie następnie,następnie,następnie itd.wedłud alfabetu.Wartość głównej liczby kwantowej n podaje się przed umownym oznaczeniem liczby kwantowej l. Ponieważ l jest zawsze mniejsza niż n , to możliwe są następujące stany elektronu:1s,2s,2p,3s,3p,3d,4s,4p,4d,4f itd.Liczba kwantowa m_l (m_l =0,±1,…,±l) jest związana z rzutem wektora momentu pędu na wyróżniony kierunek np. oś OZ.Dla danego l możliwych jest 2l+1 stanów różniących się liczbą kwantową m_{l .}

Zakaz Pauliego.Elektrony w atomie muszą różnić się przynajmniej jedną liczbą kwantową - czyli w jednym stanie kwantowym,opisanym czterema liczbami kwantowymi,może się znajdować co najwyżej jeden elektron.

Foton jest to cząstka elementarna nie posiadająca ładunku elektrycznego ani momentu magnetycznego.Masa spoczynkowa fotonu wynosi zero (m₀=o) a liczba spinowa 1 (s=1).W fizyce foton oznacza kwant pola elektromagnetycznego,np.widzialnego światła.Fotony są nośnikami oddziaływań elektromagnetycznych i są postrzegane jako fala elektromagnetyczna.W mechanice kwantowej pole elektromagnetyczne zachowuje się jak zbiór cząstek (fotonów).Światło jest z kwantowego punktu widzenia dużym strumieniem fotonów.W zależności od energi fotonów przenoszone przez nie promieniowanie ma inną nazwe poczynając od najwyższej energi fotonu mówi się o promieniowaniu gamma,rentgenowskim(promieniowaniu X),ultrafiolecie,świetle widzialnym,promieniowaniu podczerwonym (podczerwieni),mikrofalach,falach radiowych (promieniowaniu radiowym).Jednak z fizycznego punktu widzenia wszystkie te rodzaje promieniowania mają jednakową naturę.W próżni fotony poruszają się z prędkością światła.Nie trafiając na żadne przeszkody mogą przebywać wiele miliardów lat świetlnych.

Zjawisko Comptona.Zjawiskiem Comptona nazywamy zmianę długości fali elektromagnetycznej,tzn.przyjmując,że fala elektromagnetyczna o częstotliwości v i długości λ jest strumieniem cząstek (fotonów) o energii E=hv (E=hc/λ) i wartości pędu p=h/λ.Wówczas rozpraszanie fali elektromagnetycznej rozpatrywać możemy jako proces zderzenia fotonów o pędzie p_0f i energii E=hc/λ₀ ze spoczywającymi elektronami.W wyniku tego zderzenia elektron uzyskuje pęd p_e,a pęd fotonu maleje do wartości p_f.Tym samym długość rozpraszanej fali elektromagnetycznej zwiększa się do wartości λ=h/ p_f.Równocześnie o kąt θ ulega zmianie kierunek propagacji fali.Zmiana długości fali jest tym wieksza,im wiekszy jest kąt rozproszenia.Zależność zmiany długości fali od kąta rozpraszania wyznaczyć można wykorzystując prawo zachowania pędu:

oraz prawo zachowania energii:

Efekt Comptona:przed zderzeniem

Po zderzeniu

gdzie:

∆λ-zmian długości fali fotonu równa różnicy λ -λ_o ; θ-kąt rozproszenia

Fale de Broglie'a.L.DE Broglie założył,że dualizm cząstkowo - falowy jest własnością charakterystyczną nie tylko dla fali elektromagnetycznej,ale również dla cząstek o masie spoczynkowej różnej od zera.Oznacza to,że cząstki takie jak np.elektrony powinny również wykazywać własności falowe.Fale te nazwał on falami materii.Założył,że długość fali materii określona jest tym samym związkiem,który stosuje się do fotonów.Hipoteza de Broglie'a została po raz pierwszy eksperymentalnie potwierdzona w 1924 roku przez C.J.Davissona i L.G.Germera.Pokazali oni, że elektrony podobnie jak światło,mogą ulegać dyfrakcji.

Zasada nieoznaczoności opisuje jedną z podstawowych własności przyrody.Jest ona konsekwencją falowo-cząsteczkowej natury materii.Pojawia się ona,gdy opis zachowania cząstek (lub ogólnie obiektów) w mikroświecie chcemy przeprowadzić używając pojęć wziętych z makroświata.Zasada nieoznaczoności mówi o tym,że pewnych wielkości fizycznych nie można zmierzyć jednocześnie z dowolną dokładnością.Taką własność maja pęd i położenie a także inna para wielkości:energia i czas.Z im większą dokładnością znamy np.pęd cząstki tym mniejsza jest dokładność określenia położenia.Wielkości fizyczne połączone zasadą nieoznaczoności nazywamy kanonicznie sprężonymi.

Zasada nieoznaczoności:

Iloczyn nieoznaczoności pomiarów dwóch wielkości kanonicznie sprężonych A i B jest nie mniejszy od stałej Plancka ∆A∆B ≥ h

Równanie Schroedingera

gdzie:U-energia potencjalna

elektronu w polu

gdzie ε₀-przenikalność elektryczna próżni

Na rysunku przedstawiono energie potencjalną U jako funkcje odległości r elektronu od jądra

Równanie Schrodingera dla atomu wodoru.Atom wodoru składa się z jednego elektronu związanego z jądrem-protonem poprzez pryciągające oddziaływanie kulombowskie.Dozwolone stany elektronu w atomie wodoru uzyskujemy rozwiązując odpowiednie równanie Schroedingera.Występująca w tym równaniu energia potencjalna jest kulombowską energią oddziaływania dwóch naładowanych cząstek o tym samym ładunku i przeciwnych znakach:protonu o ładunku e =1.6 ∙ 10^-19C i elektronu o ładunku -e,znajdującym się w odległości r.Energia elektronu związanego w atomie wodoru.Równanie Schroedingera dla elektronu w atomie wodoru ma roawiązanie tylko dla niektórych ściśle określonych wartości energi E.Te dozwolone stany elektronu,nazywane poziomami energetycznymi,można ponumerować przy pomocy liczby naturalnej n,która nazywa sie główną liczbą kwantową.

gdzie E_n-dozwolone energie elektronu,E₁-energia stanu podstawowego,n-główna liczba kwantowa.

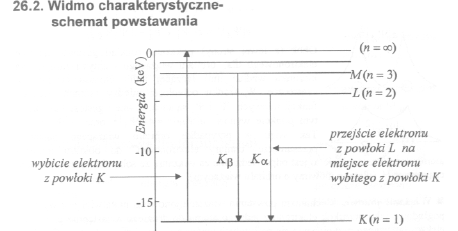
Widmo promieniowania atomu wodoru.Jeżeli do atomu wodoru dostarczymy energii z zewnątrz np.na skutek zderzenia z innym atomem albo na skutek absorbcji kwantu światła,to elektron ze stanu podstawionego może przejść na wyższy poziom energetyczny albo nawet oderwac się od atomu(atom ulegnie w ten sposób jonizacji).Elektron przebywa przez czas rzędu 10^-8s na wyższym poziomie energetycznym,a następnie wraca bądź to bezpośrednio na poziom podstawowy,bądź poprzez inne poziomy pośrednie emitując energie w postaci fotonów.Na rys.wyżej przedstawiony jest schemat powstawania serii widmowych promieniowania atomu wodoru.Zmiana energi elektronu podczas przejścia ze stanu o energi E_n do stanu o energi E_m równa jest energi emitowanej fotonu równej hv ,gdzie v jest częstością emitowanej fali.

Korzystając ze związku v=c/λ ,gdzie c jest prędkością światła otrzymujemy wzór na odwrotność długości emitowanej fali.

gdzie: Stosowana w tym wzorze stała Rydberga równa jest:
,

λ-długość emitowanej fali,

m=1,2,3… : n=m+1,m+2,m+3,…

Promieniowanie rentgenowskie. Do wytwarzania promieniowania rentgenowskiego (promieniowania X)służą lampy rentgenowskie.W starszych typach lamp rentgenowskich elektrony są emitowane przez rozżarzoną katodę wolframową,a następnie rozpędzane różnicą potencjałów potencjałów=10 ÷ 100Kv,przyłożoną między katoda a anodą.Rozpędzane przez pole elektryczne elektrony uderzają w anodę,która staje się źródłem promieni rentgenowskich.Widmo promieniowania rengrnowskiego składa się z:1).ciągłego widma hamowania;2).widma charakterystycznego,pojawiającego się,w postaci wąskich pików na tle widma ciągłego.

gdzieλ_min -minimalna wartość fali promieniowania;U-napięcie między katodą a anodą(antykatodą)lampy

23. Jama potencjału.

Rozpatrzę przypadek dla cząstki w jamie (studni) potencjału, w którym energia potencjalna pola jest równa zeru w obszarze [0,L] a po za nim Uo. Taki kształt energii potencjalnej nazywamy jamą potencjału. Dla uproszczenia Uo→ ∞ (nieskończona studnia potencjału). Wtedy dla dowolnej energii E cząstka nie może opuścić jamy potencjału tzn. ze prawdopodobieństwo tego, ze cząstka znajduje się po za obszarem [0,L] jest równa zeru. W obszarze [0,L] równanie Schroedingera ma postać taką jak dla cząstki swobodnej (gdyż x=0)

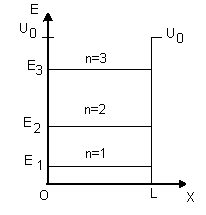
Ponieważ cząstka jest „uwieziona” w jamie potencjału, to odpowiadająca jej fala de Broglie'a będzie sumą zarówno fali biegnącej w lewo jak i w prawo.

Dozwolone energie cząstki wewnątrz nieskończonej jamy potencjału

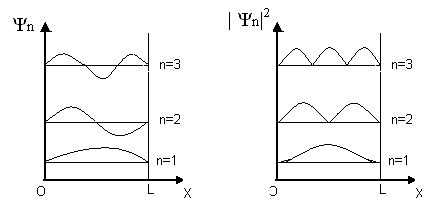
Ψn- funkcje falowe cząstki wewnątrz nieskończonej jamy potencjału

| Ψn|² - prawdopodobieństwo znalezienia cząstki w jamie potencjału

25. IZOLATORY, PÓŁPRZEWODNIKI I PRZEWODNIKI. PASMA ENERGETYCZNE.

IZOLATORY,

Ze względu na to, że przewodnictwo materiałów zmienia się w sposób ciągły nie istnieje jedna granica wartości przewodnictwa poniżej której wszystkie materiały byłyby izolatorami stosowane są różne definicje izolatora bazujące na mikroskopowym mechanizmie przewodnictwa. Przykładowo:

-izolatorem określa się substancje, dla których poziom Fermiego leży pomiędzy pasmami

-izolatorem określa się substancję, dla której przewodnictwo rośnie wraz z temperaturą, w przeciwieństwie do metalu, gdzie przewodnictwo maleje ze wzrostem temperatury.

W tym kontekście często półprzewodniki kategoryzowane są jako izolatory.

Ważnym parametrem izolatora jest jego przenikalność elektryczna. Jest to liczba wskazująca ile razy osłabnie pole elektryczne w danym dielektryku, pochodzące od jakichkolwiek ładunków, w porównaniu z polem od tych samych ładunków po usunięciu dielektryka. Za wzorzec przyjęto próżnię, gdzie jej przenikalność wynosi 1.

Półprzewodnik - nazywamy kryształ w którym w temperaturze zera bezwzględnego pasmo walencyjne jest całkowicie zajęte elektronami, a pasmo przewodnictwa całkowicie puste. Ze wzrostem temperatury w paśmie przewodnictwa pojawiają się elektrony, a w paśmie walencyjnym puste miejsca po elektronach, tzw. dziury. Dziury pod wpływem pól zewnętrznych zachowują się jak dodatnio naładowane cząstki, czyli w półprzewodniku mamy jednocześnie prąd elektronów i dziur. Półprzewodnik może być półprzewodnikiem samoistnym (ilość dziur w paśmie walencyjnym równa się ilości elektronów w paśmie przewodnictwa).albo półprzewodnikiem domieszkowym (przewaga elektronów w paśmie przewodnictwa - typ n, przewaga dziur w pasmie walencyjnym - typ p). Półprzewodnikami samoistnymi są czyste kryształy składające się np.. z atomów IV grupy układu okresowego. Natomiast półprzewodniki domieszkowe są kryształami zawierającymi dodatkowe obce atomy tzw. domieszki.

Przewodniki:

Przewodnik elektryczny to substancja, która dobrze przewodzi prąd elektryczny, a przewodzenie prądu ma charakter elektronowy. Przewodniki zbudowane są z atomów, od których łatwo odrywają się elektrony walencyjne (jeden, lub więcej), które z kolei tworzą wewnątrz przewodnika tzw. gaz elektronowy. Elektrony te ( gaz elektronowy) nie są już związane z konkretnym jonem dodatnim i mogą się swobodnie poruszać. Przewodniki znajdują szerokie zastosowanie do wykonywania elementów urządzeń elektrycznych.

Do najpopularniejszych przewodników należą (uporządkowanie wg wzrostu przewodnictwa):grafit ,żelazo ,stal

Pasma Energetyczne:

Elektrony w krysztale poruszają się w periodycznym polu potencjalnym pochodzącym od atomów tworzących sieć krystaliczną. W wyniku tego nie wszystkie energie są dozwolone. Wartość dozwolonych energii dla elektronów mają postać szeregu następujących po sobie pasm (energetycznych) rozdzielonych obszarami energii wzbronionych.

E- zależność energii od wektora falowego w przypadku periodycznego pola kryształu

k- wektor falowy elektronu

2m*- masa efektywna

26. Rozkład Fermi -Diraca -

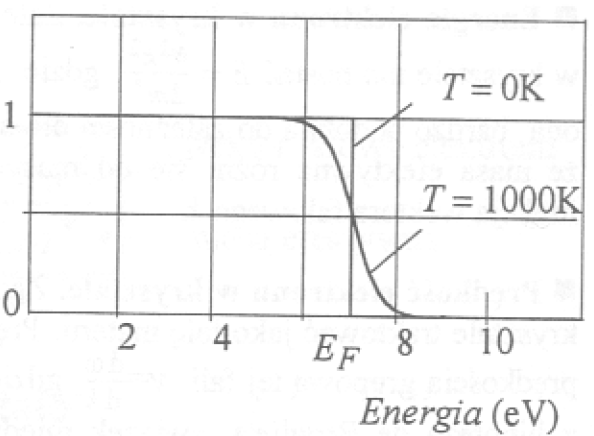
zwana także funkcja prawdopodobieństwa określa prawdopodobieństwo obsadzenia przez elektron dozwolonych stanów energetycznych. Dla T=0 funkcja rozkładu Fermiego - Diraca ma wartość 1 dla energi 0 ≤ E ≤ E_F (EF) i 0 dla energii powyżej E_F (EF). Ten charakter funkcji rozkładu można uzasadnić następująco. Zgodnie z zakazem Pauliego w jednym stanie nie mogą znajdować się więcej niż dwa elektrony różniące się orientacja spinów. W temperaturze zera bezwzględnego (T=0), elektrony zajmują kolejne stany o możliwie najniższej energii. Gdyby elektrony miały własności gazu klasycznego (brak zakazu Pauliego), to oczywiście dla T=0 wszystkie zajęłyby najniższy poziom energetyczny, czyli poziom o energii (kinetycznej) równej 0. Jednakże dla elektronów w metalu, ze względu na zakaz Pauliego, w T=0 obsadzają kolejno stany o coraz wyższej energii aż do pewnej energii maksymalnej, którą nazywamy energią Fermiego E_F (EF). Funkcja rozkładu dla T>0 różni się od funkcji dla T=0 tym, że zamiast skokowej zmiany funkcji od 1 do 0 dla energii równej E_F mamy w pobliżu energii Fermiego rozmycie termiczne funkcji rozkładu. Jest ono tym większe im wyższa jest temperatura. W metalach aż do temperatury topnienia rozmycie termiczne jest małe w porównaniu z E_F (EF) i często z dobrym przybliżeniem możemy dalej stosować funkcje rozkładu dla T=0.

Funkcja rozkładu Fermiego - Diraca

27. Złącze p-n

Złączem p-n nazywamy połączenie półprzewodnika typu p z półprzewodnikiem typu n np. gdy monokryształy krzemu zdomieszkujemy z jednej strony na typ n przez wprowadzenie atomów ln (akceptory), a z drugiej strony na typ p przez wprowadzenie atomów As (donory).

Na rysunku przedstawiłem obszar złącza `'tuz po połączeniu'' przewodnika typu n z półprzewodnikiem typu p. Złącze jest w stanie nie równowagi, gdyż w paśmie przewodnictwa koncentracja elektronów w obszarze typu n jest nieznacznie większa niż w obszarze typu p, a w paśmie walencyjnym koncentracja dziur w obszarze typu p jest większa znacznie niż w obszarze typu n. Z obszaru typu n zaczyna płynąć dyfuzyjny prąd elektronów I_nr (INR), a z obszaru typu p do obszaru tupu n prąd dyfuzyjny dziur I_pr (IPR). W druga stronę płyną prądy tzw. Nośników mniejszościowych: I_ng (ING)- prąd elektronów z obszaru typu p do n, I_pg (IPG)- prąd dziu z obszaru typu p do n. Skutkiem płynących prądów po prawej stronie AA' powstaje ujemny ładunek zjonizowanych akceptorów, a po lewej dodatni ładunek zjonizowanych donorów. W wyniku tego wewnątrz złącza p-n powstaje pole elektryczne E_w (EW) przeciwdziałające dalszej dyfuzji nośników. W stanie ustalonym sumaryczne prądy elektronów i dziur jest równe 0.

I_nr + I_ng= 0 i I_pr + I_pn= 0

Tranzystor, trioda półprzewodnikowa (obecnie głównie krzemowa), element czynny układów elektronicznych służący do wzmacniania sygnałów elektrycznych. Wśród wielu rodzajów tranzystorów najbardziej typowe są tranzystory bipolarne (iniekcyjne): dwuzłączowe i jednozłączowe, oraz tranzystory unipolarne (polowe). Najprostszy tranzystor bipolarny dwuzłączowy, zbudowany jest z dwóch złącz p-n położonych blisko siebie (kolejno obszary n-p-n lub p-n-p).

W tranzystorach n-p-n pierwszy z obszarów n połączony jest ze stykiem nazywanym emiterem (w bezpośrednim sąsiedztwie styku znajduje się duża koncentracja domieszek), obszar p z tzw. bazą, a drugi obszar n z tzw. kolektorem (analogicznie dla układu p-n-p). Złącze emiter-baza spolaryzowane jest w kierunku przewodzenia (dioda półprzewodnikowa), złącze kolektor-baza spolaryzowane jest zaporowo.

28. LASER.

Schemat ten przedstawia poziomy energetyczne trójpoziomowego lasera rubinowego. W laserze tym przejścia `'laserowe'' zachodzą miedzy poziomami jonów Cr<sup>+3</sup> wbudowanych w sieć krystaliczną Al<sub>2</sub>O<sub>3</sub> . W wyniku pompowania optycznego następuje przejście elektronów ze stanu podstawowego do jednego z dwu szerokich poziomów wzbudzonych tzw. pasm absorbcji. Tak wzbudzone elektrony `'spadają'' bardzo szybko na poziom metastabilny o stosunkowo długim czasie życia. Przejście to jest przejściem bez promienistym, a nadmiar energii oddawany jest sieci krystalicznej. Przejścia z poziomu metastabilnego na poziom podstawowy mogą wywołać powstanie akcji laserowej

Foton wyemitowany wyniku emisji spontanicznej prostopadle do powierzchni luster przebiegając obszar roboczy lasera wywołuje emisję wymuszoną wzbudzonych atomów znajdujących się na jego drodze. Powoduje to się pojawienie wiązki fotonów (fali elektromagnetycznej) rozchodzącej się prostopadle do powierzchni luster. Przy każdorazowym przejściu wiązki przez obszar roboczy lasera oddziaływuje ona ze wzbudzonymi atomami, wymuszając coraz więcej aktów emisji, zwiększając tym samym liczbę fotonów we wiązce. Wszystkie fotony mają częstotliwość polaryzacje i kierunek propagacji. Powstaje równoległa wiązka monochromatycznej fali spójnej, wiązka światła laserowego. Równoległość wiązki jest ograniczona jedynie efektami dyspersyjnymi związanymi z układem optycznym. Aby w wyniku interferencji fal rozchodzących się w przeciwnych kierunkach nie występowało ich wzajemne wygaszanie, odległość miedzy lustrami musi być taka żeby powstała fala stojąca.

24. Kwantowy oscylator harmoniczny i efekt tunelowy

Oscylator harmoniczny nazywamy cząstkę o masie m wykonująca jednowymiarowy ruch pod wpływem sprężystej siły f= -kx , gdzie k jest współczynnikiem sprężystości. Energia potencjalna cząstki ma wtedy postać U(x)=
, gdzie w jest częstością kołową drgań. W mechanice kwantowej zagadnienie drgań oscylatora harmonicznego otrzymujemy rozwiązując równanie Schroedingera, w którym jako energie potencjalną wstawimy U(x)=
, czyli:

Rozwiązując to równanie otrzymujemy energie dozwolonych poziomów energetycznych E=En. W odróżnieniu od cząstki w studni potencjału, odległości miedzy dozwolonymi poziomami energii są stałe i wynoszą hw=hv. Najmniejsza możliwa wartość energii oscylatora (np. wsieci krystalicznej ) jest rózna od zera i wynosi Eo=1/2 hv.

En= (n + ½)hv

En- dozwolone energie kwantowego oscylatora harmonicznego

v- częstotliwość drgania v=w/2Л

n- liczba naturalna

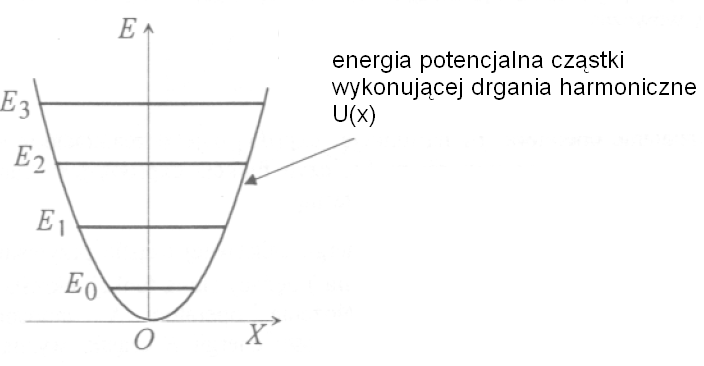
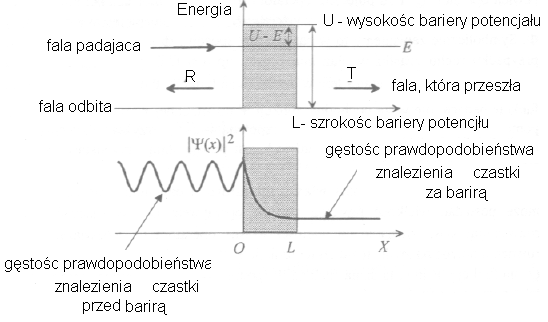
Rysunek przedstawia potencjał pola U(x) w postaci tzw. bariery energetycznej (potencjału). Ma ona kształt prostokątny o wysokości U i szerokości L.

Cząstka (elektron) zbliża się do bariery z lewej strony. W przypadku klasycznym, jeżeli energia całkowita energii E jest mniejsza niż U cząstka odbije się do bariery i będzie się poruszać się z powrotem w kierunku z którego przybyła. Według mechaniki kwantowej istnieje skończone prawdopodobieństwo tego, że cząstka pojawi się z drugiej strony bariery i będzie kontynuować ruch w prawo. Poprawny opis tunelowania cząstki otrzymuje się rozwiązując równanie Schroedingera z przedstawionym potencjałem U(x). Otrzymana z tego równania funkcja falowa służy następnie wyznaczenia gęstości prawdopodobieństwa znajdowania się cząstki w danym miejscu na osi OX. Gęstość prawdopodobieństwa jest równa kwadratowi modułu funkcji falowej
. Tak a nie inną zależność gęstości prawdopodobieństwa znalezienia cząstki przed, wewnątrz i za bariera możemy intuicyjnie zrozumieć mając na uwadze jej własności falowe. Z lewej strony bariery (x<0) mamy falę poruszającą się w prawo i falę o nieco mniejszym natężeniu poruszającym się w lewo. Te dwie fale (padająca i odbita) nakładają się dając obraz interferencyjny. Z prawej strony bariery (x > L) mamy jedynie falę poruszającą się w prawo o amplitudzie mniejszej niż fala padającą na barierę. Gęstość prawdopodobieństwa znalezienia cząstki za bariera jest stała, tak jak dla cząstki swobodnej.

Promieniowanie rentgenowskie. Do wytwarzania promieniowania rentgenowskiego (promieniowania X)służą lampy rentgenowskie.W starszych typach lamp rentgenowskich elektrony są emitowane przez rozżarzoną katodę wolframową,a następnie rozpędzane różnicą potencjałów potencjałów=10 ÷ 100Kv,przyłożoną między katoda a anodą.Rozpędzane przez pole elektryczne elektrony uderzają w anodę,która staje się źródłem promieni rentgenowskich.Widmo promieniowania rengrnowskiego składa się z:1).ciągłego widma hamowania;2).widma charakterystycznego,pojawiającego się,w postaci wąskich pików na tle widma ciągłego.

gdzieλ_min -minimalna wartość fali promieniowania;U-napięcie między katodą a anodą(antykatodą)lampy

11. INTERFERENCJA WIELU WIĄZEK. WPŁYW ILOŚCI SZCZELIN NA PRĄŻKI INTERFERENCYJNE

Interferencja światła występuje najsilniej dla fal całkowicie spójnych; jeśli np. interferują ze sobą dwie wiązki całkowicie spójne o jednakowym natężeniu I0, to natężenie wiązki wypadkowej przyjmuje jedną z wartości w przedziale od 0 do 4I0 (zależnie od różnicy faz wiązek). W przypadku fal niespójnych i.ś. nie zachodzi; jeśli np. nakładają się dwie wiązki niespójne, to natężenie wiązki wypadkowej jest zawsze sumą natężeń wiązek składowych. Ponieważ we wszystkich makroskopowych źródłach światła (z wyjątkiem lasera) promieniowanie jest emitowane w niezależnych aktach emisji światła (w gazie niezależnie przez poszczególne atomy lub cząsteczki), to światło takie odznacza się bardzo niskim względnie stopniem spójności. W celu zaobserwowania i.ś. pochodzącego z takich źródeł trzeba stworzyć warunki, w których różnice dróg nakładających się wiązek będą dostatecznie małe (mniejsze od tzw. drogi spójności). W tym celu często oświetla się małą szczelinę (lub układ bardzo bliskich szczelin), która stanowi wtórne źródło światła o wyższym stopniu spójności; taką wiązkę rozdziela się następnie na wiązki cząstkowe (wykorzystując odbicie, załamanie lub dyfrakcję światła), które będą spójne względem siebie w tym większym stopniu, im mniejsze będą różnice dróg, jakie przebyły od miejsca swych narodzin do miejsca powtórnego spotkania. Istotny wpływ na i.ś. ma także stan polaryzacji światła. Najsilniej wzmacniają się lub osłabiają przez i.ś. wiązki świetlne spolaryzowane w tej samej płaszczyźnie; wiązki spolaryzowane w płaszczyznach do siebie prostopadłych nakładają się bez wzmocnienia lub osłabienia. Na zasadzie i.ś. opiera się działanie wielu różnych urządzeń i przyrządów optycznych (np. siatki dyfrakcyjnej, -interferometru optycznego, filtrów interferencyjnych). Jednym ze zjawisk, w których występuje i.ś., były znane już w XVII w. barwy interferencyjne, które po raz pierwszy zbadał systematycznie I. Newton, wyjaśniając je jednakże na gruncie swojej korpuskularnej teorii światła.

15.Ciało doskonale czarne-ciało całkowicie pochłaniające promieniowanie elektromagnetyczne padające na jego powierzchnię. Dla ciał DC spektralna zdolność absorpcyjna jest równa1 dla każdej długości absorbowanej fali.

Doświadczenie franca-hertza

Doświadczenie polega na tym, że atomy lub cząsteczki rozrzedzonych par rtęci bombarduje się powolnymi elektronami. Najbardziej zewnętrzne elektrony sa ekstraktowane od wpływu jądra przez elektrony na wew. powłokach. W doświadczeniu odgrywają role jedynie zewnętrze elektrony. Powolne elektrony, przechodząc przez pary rtęci zderzają się z jej atomami. Jeżeli mamy do czynienia ze zderzeniami sprężystymi to wtedy atom rtęci nie pochłonął energii wskutek zderzenia a elektron zmienił tylko kierunek swojej prędkości nie zmieniając wartości. Przy zderzeniach niesprężystych cześć elektronów traci swoja energie oddając ja atomom, z którymi się zderzyły i wyniku tego rozkład wartości prędkości ulega zmianie. doświadczenie wykazał ze dopóki energia elektronów nie osiągnie pewnej charakterystycznej (krytycznej)wartości, zderzeniach z atomami rtęci są całkowicie sprężyste -przy prędkościach elektronów bliskich prędkości krytycznej zderzenie przebiega niesprężyście hV=ΔE=hc/λ

---