Drgania tłumione.

    Swobodne drgania harmoniczne stanowią przypadek drgań idealnych. Wszystkie ruchy doznają oporu, w grę wchodzi siła tarcia, gdy mamy do czynienia z ruchem po podłożu lub opór lepkości, gdy ruch odbywa się w powietrzu czy cieczy. Pokonanie sił tarcia czy lepkości wymaga zużycia energii. W przypadku ciał drgających strata energii powoduje tłumienie drgań. Przeanalizowaliśmy ruch oscylatora tłumionego, jeżeli wartość siły oporu jest proporcjonalna do wartości prędkości.
Siłę oporu można zapisać w postaci
znak "-" oznacza, że siła oporu ma przeciwny zwrot do prędkości ciała. Współczynnik γ zależy od warunków, w których ruch się odbywa, a także od rozmiarów i kształtu ciała (np. mniejszy od kształtów opływowych) Równanie opisujące drgania tłumione przyjmuje postać:

Korzystając z rachunku całkowego można udowodnić, że rozwiązaniem tego równania jest:

Amplituda drgań tłumionych wyraża się wzorem:

Ze wzoru wynika, że wartość amplitudy maleje wykładniczo w czasie.

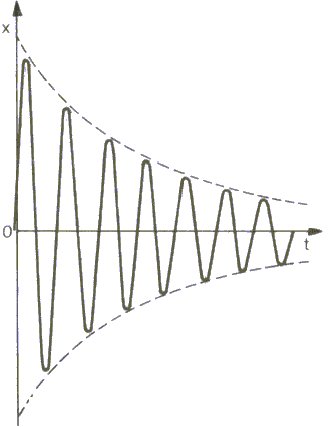
Wspomniana strata energii powoduje wygasanie drgań. Częstość drgań tłumionych można przedstawić:

gdzie ω-częstotliwość drgań własnych

Wynika ω<ω₀ a zatem T>T₀

Okres drgań tłumionych jest dłuższy od okresu drgań swobodnych (nietłumionych) zachodzących pod działaniem takiej samej siły sprężystości.
Warto zauważyć, że drgania tłumione nie są zatem ściśle biorąc drganiami periodycznymi. W ciągu jednego okresu amplituda drgań ulega zmniejszeniu.

po zlogarytmowaniu otrzymamy

Wartość tę nazywamy dekrementem logarytmicznym amplitudy.

---