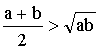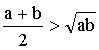Obecnie, w dobie ciągłych reform szkolnictwa, warto zastanowić się jakie są najważniejsze cele procesu nauczania - uczenia się matematyki. Jednym z nich jest wyrabianie w uczniach samodzielności. Jednakże nadal większość lekcji prowadzona jest w sposób tradycyjny, tzn. dominuje metoda podająca. Z. Putkiewicz w swej książce pt. „Pomagajmy uczniom myśleć” zwraca uwagę na przyczyny takiego stanu. Otóż, często ze względu na ograniczenia czasowe, nauczyciel chcąc przerobić materiał przepisany programem, przekazuje uczniom wiedzę w sposób werbalny. W konsekwencji, niejednokrotnie uczniowie zostają pozbawieni możliwości samodzielnego zdobywania wiadomości, porównywania faktów, szukania przyczyn. Istnieje wtedy ryzyko, że podawane im wiadomości przyjmą mechanicznie, bez przemyślenia, a co gorsze - bez zrozumienia. Autor trafnie stwierdza, iż w takiej sytuacji to nauczyciel pracuje za ucznia, gdyż stara się w sposób przystępny i zrozumiały przekazać określone partie materiału, zaś aktywność ucznia może się ograniczyć co najwyżej do próby zapamiętania pewnych faktów. Taka sytuacja wyrabia u ucznia postawę oczekiwania na wiadomości ze strony nauczyciela, rodziców czy starszego rodzeństwa.
Również wyniki nauczania okazują się niezadowalające. Prawdopodobnie jednym z powodów słabego opanowania wiadomości jest właśnie bierna postawa ucznia. „...Wiadomości, które [uczeń] zdobywa w sposób bierny, nie stają się jego własnością i nie zostają włączone w jego treść wewnętrzną. Są czymś obcym, narzuconym z zewnątrz, przyswajanym pamięciowo, często fragmentarycznie, bez możności tworzenia zwartej całości. Trzeba więc żebyśmy w istniejących warunkach starali się zmienić postawę samego ucznia, żebyśmy pomogli mu myśleć” [Z. Putkiewicz, 1964, s. 8]. Podobnie pisze Stefan Garczyński w swym dziele pt. „Jak zapamiętać”: „...wiadomości zapamiętane bez zrozumienia są niefunkcjonalne. Uczniowie, którzy uczą się tylko werbalnie, klepiąc słowa i reguły, okazują się bezradni tam, gdzie żąda się nie słów, lecz posługiwania się wiedzą. Mechanicznie wbite w pamięć definicje i uogólnienia nie dają się zastosować w zmienionym kontekście” [S. Garczyński, 1976]. Jak więc zorganizować proces nauczania i uczenia się, aby uczeń zaczął ze zrozumieniem przyswajać podawane mu wiadomości oraz podjął próbę samodzielnego zdobywania wiedzy?
Zdaniem Józefa Kozieleckiego „...Człowiek to istota poznawcza, która jest samodzielna i która nie tylko zdolna jest zrozumieć świat, ale sensownie go zmieniać. (...) Dlatego, skoro ludzie są istotami samodzielnymi, które przewidują, formułują hipotezy, eksperymentują i uogólniają podobnie jak naukowcy, to między wychowawcą a wychowankiem, między nauczycielem a uczniem musi zachodzić stosunek badawczy, czyli taki stosunek, jaki istnieje między bardziej a mniej doświadczonym naukowcem” [J. Kozielecki, 1977]. Interakcje między nauczycielem a uczniem, które najczęściej spotykamy w normalnym systemie klasowo-lekcyjnym, J. Kozielecki porównuje do relacji między mistrzem a laikiem, między ekspertem a ignorantem. W takim modelu nauczyciel jest specjalistą, który opanował obszerną wiedzę, a zatem zna wszystkie odpowiedzi na wszystkie pytania, zaś rola uczniów bardziej sprowadza się do konsumpcji wiedzy, niż do aktywnego uczestnictwa w procesie kształcenia. Należałoby więc podjąć próbę zmiany takiej sytuacji, czyli wprowadzić relacje, które powodują, że „..nauczyciel przestaje być niedoścignionym ekspertem, lecz staje się partnerem” [J. Kozielecki, 1976]. Nauczyciel i uczeń powinni wspólnie formułować problemy, stawiać hipotezy i próbować je zweryfikować. Wtedy „...Uczeń przestaje być ofiarą systemu kształcenia, lecz staje się jego współorganizatorem i aktywnym uczestnikiem” [J. Kozielecki, 1976]. Oczywiście taka zmiana stosunku między nauczycielem a uczniem jest możliwa jedynie przy modyfikacji metod nauczania i wychowania. Niewątpliwie konieczne jest ograniczenie metod podających, a rozpowszechnienie technik, które kształcą aktywność i samodzielność młodzieży. Współczesna pedagogika i dydaktyka wypracowały cały repertuar takich metod. Jedną z nich jest zwiększenie problemowości nauczania, tzn. docenienie roli zadań problemowych. Wtedy uczeń staje się badaczem, który pod kierunkiem nauczyciela odkrywa problemy, formułuje hipotezy i próbuje je uzasadnić. „...nauczanie problemowe kształtuje umiejętność produktywnego myślenia i powoduje, że wiedza staje się bardziej operatywna- znacznie łatwiej można ją zastosować w praktyce. Uczy ono jeszcze czegoś, a mianowicie postawy badawczej. Dzięki niej człowiek widzi świat nie jako doskonale zorganizowaną strukturę, lecz jako zbiór problemów, które każde pokolenie musi rozwiązać” [J. Kozielecki, 1977].
1. Problem, sytuacja problemowa, zadanie problemowe
By móc mówić o wykorzystaniu zadań problemowych w procesie nauczania-uczenia się matematyki, należy sprecyzować znaczenie samego pojęcia „zadanie problemowe”. Otóż okazuje się, iż termin ten bywa różnie rozumiany, a tym samym posiada kilka definicji. Czesław Kupisiewicz zwraca uwagę na fakt, iż „...problemy nie istnieją niezależnie od ludzi, że rodzą się one w przypadku powstawania rozbieżności między postawionymi celami a wiedzą określonego człowieka” [Cz. Kupisiewicz, 1973, s. 32]. Z.Pietrasiński stwierdza w książce pt. ”Psychologia sprawnego myślenia”, że problem powstaje wtedy, „...gdy działalność skierowana jest na osiągnięcie jakiegoś celu, lecz droga do tego celu nie jest znana, przynajmniej nie jest znana w pełni, tak że osiągnięcie celu wyłącznie w oparciu o działania instynktowne lub nawykowe jest niemożliwe” [Z. Pietrasiński, 1959, s. 75]. Jednakże Z. Krygowska w trzeciej części „Zarysu dydaktyki” zwraca uwagę na potrzebę odróżnienia sytuacji problemowej od zadania pojawiającego się na tle tej sytuacji. I tak możemy wyszczególnić dwa rodzaje sytuacji problemowej: naturalną sytuację, nie zorganizowaną przez nauczyciela lub też przeciwnie- sytuację celowo zorganizowaną przez nauczyciela. Naturalna sytuacja polega na zaobserwowaniu przez uczniów fragmentu rzeczywistych układów rzeczy, stosunków, zjawisk. W przytoczonym przez Z. Krygowską przykładzie, dzieci zainteresowały się loterią fantową, którą organizował pewien kupiec. Wśród ponumerowanych fantów znajdowały się przedmioty bardzo drogie, ale też przedmioty o małej wartości. Losowanie odbywało się przez rzucanie sześciu kostek do gry. Suma wyrzuconych oczek wskazywała numer wygranego fantu. Dzieci zapytały nauczyciela, jak to możliwe, że kupiec zarabia na takiej loterii, mimo iż udział w grze kosztuje bardzo mało, a wśród losowanych przedmiotów znajdują się przedmioty bardzo drogie. Widać więc, iż powstała tu sytuacja problemowa, która nie była świadomie zorganizowana przez nauczyciela. Jednakże sama obserwacja, której dzieci dokonały, to jeszcze nie jest zadanie. Dopiero na tle tej sytuacji, w wyniku nasuwających się pytań, powstają zadania problemowe: Dlaczego tak jest? Co z tego wynika? Co jest lepsze, praktyczniejsze? Co można powiedzieć? [Z. Krygowska, 1980]
Przykładem drugiego rodzaju sytuacji problemowej, tzn. sytuacji świadomie zorganizowanej przez nauczyciela, jest następująca zabawa zwana „biegiem do liczby”. Uczniowie grają parami. Osoba rozpoczynająca może powiedzieć liczbę 1 lub 2. Następnie, przeciwnik podaje liczbę o 1 lub 2 większą od tej, którą powiedział poprzednik. I tak na przemian zawodnicy mówią liczby, a wygrywa ten, który pierwszy powie 21. Po kilku grach uczniowie prawdopodobnie zaczną się nudzić, jednak wtedy nauczyciel może zaproponować, iż potrafi ograć każdego z uczniów. Po kilku udanych rozgrywkach między nauczycielem a uczniami nasuwa się więc pytanie: Czy rzeczywiście istnieje strategia wygrywająca? Jaka?
Dlaczego jednak przy omawianiu zadań problemowych tak ważne jest właściwe rozumienie sytuacji problemowej? Otóż, zarówno w nauce jak i w życiu codziennym, zwykle najpierw pojawiają się sytuacje problemowe, a dopiero na ich tle formułujemy pewne problemy. Jak pisze Cz. Kupisiewicz „Punkt wyjścia(...) problemu stanowi sytuacja problemowa, tzn. sytuacja, która wprawia podmiot w stan zakłopotania, wywołuje uczucie trudności połączone z ciekawością oraz budzi chęć zaspokojenia go. Analiza tej sytuacji prowadzi do sformułowania problemu, a więc do słownego określenia napotkanej trudności” [Cz. Kupisiewicz, 1973, s. 35]. Cz.Kupisiewicz uważa również, iż o problemie możemy mówić wtedy, gdy „...nasz dotychczasowy zasób wiedzy, łącznie z umiejętnościami, okazuje się niewystarczający dla osiągnięcia założonych celów np. dla poznania przyczyn takiego czy innego zjawiska, znalezienia „wyjścia” z trudnej sytuacji, podjęcia optymalnej decyzji itp. Stąd też problemy mają z reguły charakter podmiotowy, są zadaniami, których rozwiązanie wymaga od podmiotu wykonania operacji umysłowych zarówno aktywizujących, jak i wzbogacających jego wiedzę” [Cz. Kupisiewicz, 1973, s. 33]. Podobnie pisze J. Kozielecki w pracy pt. ”Rozwiązywanie problemów”: „...problem jest rodzajem zadania (sytuacji), którego podmiot nie może rozwiązać za pomocą posiadanego zasobu wiedzy. Rozwiązanie jego jest możliwe dzięki czynności myślenia produktywnego, która prowadzi do wzbogacenia wiedzy podmiotu” [J. Kozielecki, 1969, s. 16].
Zadanie problemowe można również przedstawić w sposób bardziej opisowy, tzn. określając jego cechy. Otóż, zadanie tego typu - jak pisze Cz. Kupisiewicz - „...implikuje poszukiwanie, wymaga od podmiotu badawczej postawy, a więc zebrania i oceny danych pomocniczych i głównych, sformułowania jednej lub kilku hipotez dotyczących rozwiązania analizowanej trudności, umotywowanego wyboru hipotezy w przypadku istnienia hipotez sprzecznych, sprawdzenia hipotezy przyjętej” [Cz. Kupisiewicz, 1973, s. 34]. Drugą ważną cechą jest fakt, iż podstawa rozwiązania zadania problemowego to myślenie produktywne, którego efektem jest „nowe poznanie”. Oznacza to, iż w wyniku pokonania trudności pojawiającej się w zadaniu problemowym, następuje wzbogacenie dotychczasowego zasobu wiedzy i umiejętności, poprzez zdobycie nowych lub przestrukturyzowanie starych wiadomości. Jest to bardzo istotne, bowiem „...proces myślenia produktywnego zachodzi tylko w trakcie rozwiązywania problemów: nie można myśleć produktywnie w sytuacjach, w których nie występują problemy...” [J. Kozielecki, 1992, s. 120-121]. Jednocześnie, niezbędne jest również myślenie reproduktywne, polegające na aktywizowaniu zdobytych wcześniej treści. Przede wszystkim jednak, rozwiązywanie zadań problemowych przyczynia się do przyswojenia sobie wiedzy czynnej, czyli takiej, która jest niezbędna przy wykonywaniu czynności nowych, z którymi wcześniej nie spotkano się. Zapobiega to sytuacji, w której uczący się zdobywa wiedzę bierną, bowiem taka wiedza przydatna jest jedynie w sytuacjach typowych, standardowych (np. udzielanie odpowiedzi na pytania zadawane z zewnątrz) i nie można wykorzystać jej w zmienionym kontekście. [Cz. Kupisiewicz, 1973]
Zatem w świetle powyższych rozważań, zadanie problemowe to zadanie, które zawiera w sobie nową trudność, co oznacza, że nie można go łatwo rozwiązać znanymi dotychczas środkami, gdyż nie jest znany gotowy schemat rozwiązania. Aby rozwiązać takie zadanie, trzeba pokonać pojawiającą się w nim trudność. Niewątpliwie wiąże się to z dużym wysiłkiem umysłowym. Wymaga zaktywizowania posiadanej wiedzy i przeprowadzenia szeregu operacji myślowych.
Widać więc, że zgodnie z tak przyjętą definicją zadanie zbyt łatwe nie będzie dla ucznia problemem, bowiem nie zawiera ono trudności, którą uczeń musiałby pokonać. Co więcej - takie zadanie nie wzbudzi u ucznia żadnego zainteresowania. Jednocześnie zadanie zbyt trudne, tzn. takie, którego rozwiązanie nie znajduje się w zakresie możliwości danego ucznia, również nie będzie dla niego problemem, gdyż po prostu nie rozwiąże go. Uczeń zniechęci się do rozwiązania i nie nastąpi realizacja głównego celu, tzn. aktywizacji procesu myślenia. Zatem, jak pisze Z. Putkiewicz, „...Zadanie postawione przed uczniem będzie wtedy problemem, jeżeli znajdzie się w granicach jego możliwości, a ściśle mówiąc, będzie trochę przerastało możliwości” [Z. Putkiewicz, 1964, s. 31].
Niestety tak przyjęta definicja nie pozwala na to, by móc każde zadanie jednoznacznie określić jako problemowe lub nie. Zważywszy na fakt, że dwaj uczniowie mogą posiadać różne zasoby wiadomości i umiejętności, coś, co dla jednego z nich jest trudnością, nie musi nią być dla drugiego. Ponadto, nawet w przypadku tego samego ucznia niemożliwa jest taka klasyfikacja zadań, bowiem nieustannie poszerza on swą wiedzę i „...To, co kiedyś było dla niego problemem może z czasem przestać nim być.” [Cz. Kupisiewicz, 1973, s. 35]. Poza tym, w przyjętej definicji zadania problemowego mówi się o „nowej trudności”. Zatem, jeśli uczeń rozwiąże dane zadanie problemowe, tzn. pokona wspomnianą trudność, rozwiązując drugi raz podobne zadanie nie będzie już ono dla niego zadaniem problemowym, gdyż zna już sposób pokonywania pojawiającej się trudności. Problem jest więc pojęciem wyjątkowo subiektywnym i zawsze należy mieć na uwadze fakt, iż „...Nie znając zasobu wiedzy człowieka, nie możemy powiedzieć, czy jakieś zadanie - nawet bardzo skomplikowane - będzie dla niego problemem. Problem jest bowiem określoną relacją między zadaniem a zasobem wiedzy człowieka...” [J. Kozielecki, 1992, s. 120].
2. Problem w ujęciu psychologicznym
Oprócz właściwej interpretacji pojęcia „zadanie problemowe”, konieczna jest również ogólna znajomość procesu rozwiązywania tego typu zadań. Niewątpliwie warto zastanowić się jak przebiega proces rozwiązywania problemu w ujęciu psychologicznym. J.Kozielecki wyszczególnia cztery etapy. Zgodnie z tym, o czym wcześniej pisałam, najpierw pojawia się sytuacja problemowa. Jednakże proces rozwiązywania problemu rozpocznie się dopiero w chwili uświadomienia sobie pojawiającego się problemu. Zatem pierwszy etap, to „dostrzeganie problemu”. W momencie napotkania trudności, tzn. np. zjawiska, którego nie potrafimy sobie wytłumaczyć, sytuacji, której nie sposób rozwiązać za pomocą posiadanych nawyków czy też zauważenia pewnych sprzeczności, zaczyna działać proces myślenia. „...podmiot (...) uświadamia sobie, że zasób jego wiedzy nie wystarcza do osiągnięcia planowanych celów” [J. Kozielecki, 1992, s. 123]. Okazuje się, iż dostrzeganie problemów to wielka umiejętność. „...Wybitny fizyk, Einstein, (...) chcąc podkreślić ważność samodzielnego stawiania problemów pisał, iż "czegokolwiek by nie robiła maszyna, nawet będąc w stanie rozwiązać dowolny problem nigdy nie będzie umiała postawić choćby jednego problemu"” [J. Kozielecki, 1969, s. 28].
Drugi etap, to „analiza sytuacji problemowej”. „...w fazie tej człowiek analizuje informacje zawarte w sytuacji problemowej oraz strukturę celu, który ma osiągnąć. Bada, jakie są rozbieżności i luki między tym, co jest dane, a tym, co jest pożądane” [J. Kozielecki, 1992, s. 123]. Jest to bardzo istotny etap, gdyż precyzyjne sformułowanie celu to niezbędny warunek dalszej działalności, bowiem nadaje jej właściwy kierunek. Wiedząc co chcemy osiągnąć, wiemy jednocześnie jakie dane są do tego konieczne. Umożliwia to wyróżnienie danych istotnych, danych zbędnych i danych brakujących. Czasami jest to bardzo trudne, część ważnych informacji może być zamaskowana. Ponadto, często ludzie wykazują tendencję do preferowania danych pozytywnych, tzn. takich, które są w postaci sądów twierdzących. W efekcie nie analizują danych negatywnych, czyli mówiących o tym, czego nie ma w danej sytuacji, a tym samym znaczna część cennych informacji nie zostaje wykorzystana.
Dopiero po takiej wnikliwej analizie sytuacji problemowej rozpoczyna się zasadniczy akt rozwiązywania problemu, który powoduje konieczność stosowania całego systemu operacji intelektualnych, które mają doprowadzić do osiągnięcia postawionego celu, jakim jest pokonanie sformułowanej trudności. Etap ten zwykle nazywa się „stawianiem hipotez” lub „wytwarzaniem pomysłów”, gdyż w czasie jego trwania wysuwamy hipotezy, przypuszczenia o rozwiązaniu. Innymi słowy jest to faza pomysłów, przewidywań.
Następnie, mając pewne pomysły na rozwiązanie należy sprawdzić, które z nich są słuszne. Ten etap „weryfikowania hipotez” („weryfikowania pomysłów”) uświadamia niejednokrotnie, iż hipotezy, które intuicyjnie wydawały się najbardziej prawdopodobne, w drodze rozumowania mogą okazać się fałszywe. Istnieją dwie metody weryfikacji. Jedną z nich jest weryfikacja sukcesywna, która polega na tym, iż po sformułowaniu hipotezy rozwiązania, natychmiast sprawdzana jest jej słuszność. Jeśli postawiona hipoteza okaże się prawdziwa, proces weryfikacji zostaje zakończony. Jeśli jednak hipoteza nie doprowadziła do osiągnięcia pożądanego celu, niezbędne jest wytworzenie innego pomysłu na rozwiązanie, a następnie sprawdzenie jego poprawności. Proces weryfikacji kończy się dopiero w momencie, gdy jedna z hipotez okaże się prawdziwa i zostanie przyjęta jako ostateczne rozwiązanie. Druga metoda to weryfikacja jednoczesna. Najpierw zostaje wytworzony zbiór kilku propozycji rozwiązań, a dopiero później sprawdza się ich słuszność.
W fazie weryfikacji hipotez mogą pojawić się pewne osobliwości i paradoksy, które utrudniają racjonalną ocenę poprawności wytworzonych pomysłów. Jedną z takich osobliwości jest „efekt emocjonalny” (tendencyjność psychologiczna), tzn. po sformułowaniu pewnej hipotezy, jej autor często wykazuje wobec niej „ojcowski afekt”, czyli stara się wszystkie informacje (nawet zaprzeczające) tak interpretować, by potwierdziły postawioną hipotezę. Inną osobliwością fazy weryfikacji jest „efekt pierwszeństwa”, tzn. przecenianie wartości danych początkowych, a niedocenianie informacji otrzymywanych później.
Proces myślowy zostaje zakończony sądem przyjmującym jedną z hipotez. Jest to ogólny schemat procesu rozwiązywania problemu, co nie oznacza, że wszystkie fazy są konieczne. Przykładem takiej sytuacji jest dobrze sformułowane zadanie problemowe, które uczeń otrzymuje od nauczyciela. Wtedy zostaje pominięta faza „dostrzegania problemu” przez ucznia. Okazuje się, że jedynie faza „formułowania hipotez” jest niezbędna, zaś pozostałe etapy mogą być pominięte, zależy to jednak od struktury danego problemu oraz możliwości intelektualnych osoby rozwiązującej zadanie. Poza tym, nie zawsze proces rozwiązywania problemu przebiega w sposób „liniowy”, tzn. tak, iż z danej fazy nigdy nie wraca się do fazy poprzedniej. Często konieczne jest „cofanie się” (np. jeśli osoba rozwiązująca zadanie „utknie” w fazie „stawiania hipotez”, zwykle wraca do wcześniejszego etapu, czyli jeszcze raz próbuje dokładnie zanalizować dany problem). Poza tym, również w opisanej wcześniej sukcesywnej metodzie weryfikacji hipotez, po stwierdzeniu, iż dany pomysł jest zawodny, następuje powrót do poprzedniej fazy, tzn. fazy stawiania hipotez.
J.Kozielecki wyróżnił cztery typy problemów. Problemy typu 1 to tzw. dobrze określone czyli takie, które w sytuacji początkowej posiadają wszystkie niezbędne dane oraz jednoznacznie określony cel, tzn. istnieje tylko jedno poprawne rozwiązanie. Drugi typ problemów to takie, które również posiadają wszystkie potrzebne informacje początkowe, jednak - w odróżnieniu od typu 1 - istnieje więcej niż jedno właściwe rozwiązanie. Problemy, dla których istnieje tylko jedno rozwiązanie, jednak dane początkowe są częściowo lub całkowicie niedostępne, to trzeci typ. I wreszcie ostatnia grupa problemów (typ 4) to takie, których struktura jest najmniej sprecyzowana, tzn. nie zawierają wszystkich niezbędnych informacji i również cel nie jest jednoznacznie określony, czyli istnieje wiele rozwiązań. [J. Kozielecki, 1969]
W psychologii wyszczególnia się dwa sposoby uczenia się rozwiązywania problemów. Pierwszy z nich to „metoda prób i błędów”. Zgodnie z omówionym wcześniej procesem rozwiązywania problemów, po uświadomieniu i sformułowaniu problemu zaczynamy stawiać różne hipotezy, tzn. szukamy sposobu, który pozwoli nam pokonać pojawiającą się trudność. Podejmujemy kolejne próby rozwiązania, z których część może zakończyć się powodzeniem, a część niestety nie doprowadzi do pożądanego efektu. Te próby, które zakończyły się sukcesem, zostają wzmocnione pozytywnie i zapamiętane, a zatem utrwalają się. Jeśli jednak podjęta próba zakończyła się porażką, oznacza to, iż nastąpiło wzmocnienie negatywne i ostatecznie taki sposób, którym chcieliśmy osiągnąć cel, jest eliminowany. Ta metoda przypomina bardziej rozbudowane warunkowanie instrumentalne, które polega na tym, że pojawia się pewien bodziec wywołujący reakcję, po której następuje nagroda (wzmocnienie pozytywne) lub kara (wzmocnienie negatywne). Nagrodzone reakcje utrwalają się, zaś ukarane zostają zablokowane. W przypadku rozwiązywania problemu bodźcem jest pojawiająca się trudność i chęć pokonania jej. Próby rozwiązania to reakcja, która zostaje nagrodzona jeśli doprowadziła do pożądanego wyniku lub zostaje wzmocniona negatywnie w przypadku zakończenia się porażką. „Metoda prób i błędów” jest typowa dla problemów stosunkowo łatwych, tzn. takich, gdzie zasób możliwości („pomysłów na rozwiązanie”) jest skończony i niewielki.
Inny sposób uczenia się rozwiązywania problemów, to „uczenie się przez wgląd”. Przy tym sposobie również podejmujemy różne próby rozwiązania, jednak żadna z nich nie prowadzi do celu. W efekcie, nie mając już żadnego pomysłu na rozwiązanie, porzucamy nie rozwiązany problem (przerywamy proces rozwiązywania), przestajemy uczyć się. Następuje więc przerwa, po której nagle, „jednym błyskiem myśli” rozwiązujemy porzucony problem. Zjawisko takiego „olśnienia” może się zdarzyć zarówno słabemu uczniowi jak i znakomitemu uczonemu. Potwierdzeniem tego faktu mogą być przytoczone przez J. Kozieleckiego słowa wybitnego matematyka C. F. Gaussa, który przez wiele lat próbował rozwiązać pewien problem matematyczny: „...W końcu dwa dni temu udało mi się... Rozwiązanie zagadki zjawiło się jak błysk światła. Nie potrafię wyjaśnić, jaka nić przewodzenia związała moje uprzednie wiadomości z tymi, które umożliwiły mi osiągnąć ten sukces” [J. Kozielecki, 1992, s. 132]. Cechą charakterystyczną takiego uczenia się jest to, iż wiadomości zdobyte „przez wgląd” są znacznie trwalsze niż przy uczeniu się „metodą prób i błędów”. Zwykle jeśli ktoś rozwiąże pewien problem „przez wgląd”, rozwiązanie zostaje tak mocno utrwalone, iż osoba ta nie powinna mieć w przyszłości trudności z rozwiązywaniem zagadnień podobnego typu. Oczywiście czasami może się zdarzyć, iż pomysł, który pojawia się jako „olśnienie” jest nieskuteczny. Niemniej, jest to niezwykle intrygujące zjawisko.
Na gruncie psychologii istnieją trzy hipotezy próbujące wyjaśnić uczenie się „przez wgląd”. Pierwsza z nich, to „hipoteza przyspieszonej pracy umysłu”. Głosi ona, iż w momencie przerwania procesu rozwiązywania danego problemu nie zanika praca umysłu, a wszystkie operacje umysłowe (przetwarzanie informacji) przebiegają tak szybko, że pamięć nie jest w stanie tego zarejestrować. Dlatego też, uświadamiamy sobie dopiero ostateczny wynik, czyli prawidłowe rozwiązanie.
Druga hipoteza psychoanalityczna, to „hipoteza nieświadomej pracy umysłu”, która przyjmuje, iż operacje myślowe zachodzą dosyć wolno, ale poza naszą świadomością, więc nie rejestrujemy ich. Jest to jednak hipoteza bardzo trudna czy wręcz niemożliwa do sprawdzenia.
I wreszcie trzecia hipoteza, to „hipoteza występowania otamowania”. Otóż, jeśli rozwiązujemy dany problem, mogą pojawić się pewne otamowania, tzn. błędne nawyki, nastawienie, które maskują prawidłową reakcję. Przykładem może być sytuacja na klasówce, gdy uczeń chce rozwiązać zadanie wiedząc, że pozostało mu zaledwie kilka minut. Zwykle będzie on podejmował kolejne próby rozwiązania, które jednak będą spolaryzowane wokół tego samego, nieskutecznego sposobu. Zasugerowany tym jednym pomysłem, uczeń nie potrafi „oderwać się” od przyjętej strategii i wielokrotnie powtarza ten sam błąd. Również silne emocje takie jak strach, lęk przed niepowodzeniem, powodują „zablokowanie” umysłu. Dopiero gdy nastąpi pewien przełom, tzn. zanikną owe otamowania, jesteśmy w stanie uświadomić sobie inne hipotezy, sposoby rozwiązania. Dlatego też, często zdarza się, iż zdolny uczeń, który na lekcjach wyróżnia się aktywnością i pomysłowością, na klasówce, która niewątpliwie jest dla niego sytuacją stresową, ma problemy z rozwiązaniem zadań. Podobnie dzieje się na egzaminie, kiedy to w momencie wyjścia z sali egzaminacyjnej student natychmiast uświadamia sobie odpowiedź na pytanie, które na egzaminie stanowiło dla niego trudność nie do pokonania.
Zdaniem psychologów, wszystkie te hipotezy są prawdziwe i nie wykluczają się wzajemnie. Jak już wspomniałam, nie udało się jeszcze sprawdzić słuszności hipotezy „nieświadomej pracy umysłu”, jednak hipotezy: „przyspieszonej pracy umysłu” i „występowania otamowania” zostały potwierdzone eksperymentalnie.
3. Czynniki wpływające na sposób rozwiązywania problemów. Heurystyka rozwiązywania zadań problemowych
Wcześniejsze rozważania dotyczyły ogólnego schematu rozwiązywania problemów. Dla nauczyciela jednak najbardziej istotne jest rozwiązywanie, a ściślej mówiąc - uczenie rozwiązywania szczególnego rodzaju problemów, tzn. zadań problemowych. Umiejętność rozwiązywania tego typu zadań zależy od kilku czynników. J. Kozielecki wyróżnia trzy najważniejsze. Niewątpliwie jednym z nich jest inteligencja (zdolności intelektualne), tzn. „...cechy psychiczne (głównie właściwości myślenia), które są warunkiem sprawnego wykonywania nowych zadań różnego typu” [J. Kozielecki, 1975, s. 159]. Można więc wymienić najistotniejsze cechy umysłu, które określają poziom inteligencji danej osoby oraz ułatwiają rozwiązywanie problemów:
„zdolność dostrzegania subtelnych stosunków oraz związków między zjawiskami;
plastyczność i giętkość myślenia, tzn. umiejętność przystosowywania swej strategii psychologicznej do ciągle zmieniających się warunków;
zdolność do abstrakcyjnego myślenia, do oderwania się od konkretnych przedmiotów i operowania symbolami oraz abstrakcyjnymi pojęciami;
ekonomia myślenia, czyli rozwiązywanie problemów najprostszą drogą za pomocą możliwie najmniejszego wysiłku intelektualnego;
zdolność do pracy w warunkach trudnych, np. przy małej liczbie informacji, pod presją czasową i społeczną;
pomysłowość i oryginalność, czyli chodzenie własnymi drogami myślowymi;
umiejętność podejmowania najkorzystniejszych decyzji;
łatwość i szybkość uczenia się, czyli chłonność umysłu;
odporność na czynniki emocjonalne, które często przeszkadzają w czasie rozwiązywania ważnych problemów;” [J. Kozielecki, 1975, s. 159-160].
Drugi czynnik wpływający na sposób rozwiązywania problemu, (w szczególności zadań problemowych) to motywacja. J. Kozielecki formułuje ogólne prawo, tzn. stwierdza, że „...przy średniej motywacji do rozwiązywania problemów podmiot osiąga najlepsze wyniki, motywacja zaś zbyt słaba lub zbyt silna powoduje zmniejszenie skuteczności procesu myślenia” [J. Kozielecki, 1969, s. 33]. Brak motywów do rozwiązywania zadania powoduje, że nawet zdolni uczniowie pracują poniżej swoich możliwości. Dla podkreślenia faktu, iż motywacja jest niezbędna do sprawnego rozwiązywania problemów, J. Kozielecki przytacza słowa T. Tomaszewskiego: „...chcemy napoić konia i dajemy mu wodę, koń jednak nie pije. Próbujemy różnych środków: zmieniamy wiadro na wygodniejsze i czyściejsze, dodajemy do wody cukru itd. Koń ciągle nie pije. Aż wreszcie wpadamy na myśl, że może mu się nie chce pić.” [J. Kozielecki, 1975, s. 167]. Jednakże zbyt silna motywacja powoduje powstanie napięć emocjonalnych, czyli tzw. otamowań, które utrudniają osiągnięcie pożądanego celu.
Trzeci czynnik decydujący o umiejętności rozwiązywania problemów, to doświadczenie, czyli wiedza, „...umiejętności i nawyki, które człowiek zdobył w ciągu swego życia...” [J. Kozielecki, 1975, s. 164] lub innymi słowy - „...wynik procesu uczenia się, (...) wielowymiarowy bagaż intelektualny, który znakomicie ułatwia nam rozwiązywanie nowych zadań” [J. Kozielecki, 1975, s. 165]. Znaczna część wiedzy, którą człowiek posiada, pochodzi ze szkoły. Dlatego tak istotne jest by umożliwić uczniom zdobycie jak najbogatszego doświadczenia w rozwiązywaniu problemów.
Zgodnie z przyjętą definicją zadania problemowego, dla tego typu zadań nie istnieje algorytm, czyli „...niezawodny przepis, który określa, jaki skończony ciąg operacji należy wykonać kolejno, aby rozwiązać wszystkie zadania danej klasy” [J. Kozielecki, 1992, s. 110]. Zatem, tym bardziej istotne jest by uczniowie jak najlepiej poznali metody heurystyczne dla zadań problemowych, tzn. „...wszelkie reguły, zasady, taktyki, strategie, tricki i intuicje, które regulują przebieg procesu produktywnego, lecz które nie gwarantują osiągnięcia planowanego wyniku...” [J. Kozielecki, 1969, s. 53]. Jak wynika z takiej definicji, metody te są zawodne, jednak zgodnie ze znaczeniem słowa „heurystyczny”, czyli „sprzyjający odkryciu”, są to metody, które sprzyjają odkryciu rozwiązania.
Inicjatorem współczesnego nurtu heurystyki jest G. Polya, który w swej pracy pt. „Jak to rozwiązać” sformułował cztery punkty konieczne przy rozwiązywaniu zadań (głównie problemowych):
Próbując porównać te etapy z omówionym w rozdziale 2 ogólnym schematem rozwiązywania problemów, można powiedzieć, iż punkt pierwszy, tzn. „patrz i myśl”, jest odpowiednikiem fazy „analizy sytuacji problemowej”. Uświadomienie uczniom roli tego etapu jest bardzo istotne, bowiem zapobiega sytuacjom, kiedy to np. w przeprowadzonych badaniach, dzieci otrzymały zadanie tekstowe bez pytania, a mimo tego usiłowały je rozwiązać. Oczywiście czasami celowo nie zadaje się konkretnego pytania, a jedynie zostaje stworzona sytuacja problemowa. Wtedy jednak konieczne jest najpierw sformułowanie problemu, a dopiero później podejmuje się próby rozwiązania. W przeprowadzonych badaniach dzieci nie odczuwały potrzeby takiego określenia celu działania, jedynie w przypadkowy sposób wykonywały operacje na liczbach. Wynikało to z przekonania, iż skoro są pewne dane, to trzeba je wykorzystać, natomiast sposób wykorzystania tych danych nie miał dla nich znaczenia, był zupełnie dowolny. Zatem, główne zalecenie pierwszego etapu można sformułować w następujący sposób: „Rozpoczynaj rozwiązywanie zadań od dokładnej analizy celu, który chcesz osiągnąć. Dopiero po zrozumieniu celu zbadaj dane początkowe” [J. Kozielecki, 1992, s. 111].
Ucząc ucznia rozwiązywania zadań problemowych, musimy więc przyzwyczajać go do zadawania sobie pytań takich jak: Co jest niewiadome? Co jest dane? Jaki jest warunek? Czy warunek wystarcza do określenia niewiadomej (może jest zbyt obszerny lub sprzeczny)? Czy zadanie zawiera wszystkie dane konieczne? Które dane są konieczne? Początkowo nauczyciel musi sam stawiać tego typu pytania. Ważne jest jednak by były one mocno akcentowane i zadawane świadomie, tzn. aby uczeń rozumiał konieczność stawiania takich pytań. Tylko wtedy jest nadzieja, iż po pewnym czasie uczeń sam będzie zadawał takie pytania. Dlatego też, istotne jest by w przyszłości rozwiązując zadanie problemowe na lekcji uczniowie mieli czas na przeprowadzenie takiego dialogu wewnętrznego, czyli na postawienie sobie samym odpowiednich pytań (co oznacza właściwą analizę zadania).
Zważywszy na fakt, iż przedstawione tu metody heurystyczne mają służyć rozwijaniu umiejętności rozwiązywania nie tylko zadań problemowych, ale problemów w ogóle, czyli np. również tych z życia codziennego, umiejętność odróżniania danych koniecznych od danych zbędnych lub brakujących odgrywa ogromną rolę. Na co dzień najczęściej spotykamy się z sytuacjami, w których część informacji nie jest związana z problemem, brakuje istotnych danych. W życiowych problemach pojawiają się również dane niepewne, nieokreślone, prawdopodobne. Okazuje się, iż uczniowie mają ogromne trudności z właściwą analizą danych. Potwierdza to eksperyment amerykańskiego psychologa G.Buswella, który dał uczniom do rozwiązania dwa zadania:
Zadanie1
Człowiek kupił 7 znaczków w dniu 29 maja, wręczając urzędnikowi pół dolara. Ile otrzymał on reszty?
Zadanie 2
Dnia 14 stycznia Iks i jego syn, który miał 17 lat, pojechali na jarmark z owcami. Owce zostały sprzedane po 35 centów za funt. Ile pieniędzy otrzymali, skoro ciężar jednej owcy przeciętnie wynosił 60 funtów?
W obu zadaniach uczniowie mieli wyróżnić informacje istotne, zbędne i brakujące. Niestety sprawiło to wiele kłopotów. Stosunkowo najlepiej uczniowie poradzili sobie z wyodrębnieniem danych ważnych, więcej błędów popełnili przy wyszczególnieniu danych zbędnych, zaś największą trudnością było określenie danych brakujących. [J. Kozielecki, 1975]
J. Kozielecki zwraca uwagę na fakt, iż często ludzie (zwłaszcza dzieci) „Dostrzegają fakty tam, gdzie ich nie ma, przyjmują za wskazówkę to, co nią nie jest. Podwyższając na siłę ilość informacji, można nie rozwiązać danego problemu. Zatem, podstawowym zadaniem szkoły w trakcie uczenia dzieci rozwiązywania problemów w takich sytuacjach jest wyeliminowanie tej niebezpiecznej tendencji poznawczej i zapoznanie uczniów ze sztuką szukania właściwych, trafnych informacji i z umiejętnym wykorzystywaniem ich w różnych sytuacjach” [J. Kozielecki, 1975, s. 122].
Jak tego dokonać? Po pierwsze - przyzwyczajać uczniów do zadawania omówionych wcześniej pytań, czyli do prowadzenia dialogu wewnętrznego. Po drugie - należy dostarczać uczniom zadań, w których występują różne dane, nie tylko te logiczne, całkowicie pewne. Po trzecie - warto zapoznać uczniów z głównymi operacjami, które biorą udział w tym pierwszym etapie „patrz i myśl”. Właściwie nie istnieje jedna, ogólna klasyfikacja operacji umysłowych, jednak najbardziej znana to ta, którą stworzyli rosyjscy psychologowie, głównie S. L. Rubinsztejn oraz A. Smirnow. Ich zdaniem można wyróżnić dwa podstawowe rodzaje operacji: analizę i syntezę, zaś wszystkie pozostałe, tzn. porównywanie, abstrahowanie i uogólnianie są ich pochodnymi. I tak, „...Analiza jest to myślowe rozdzielanie, rozczłonkowywanie przedmiotu lub zjawiska na poszczególne elementy składowe lub momenty danej sytuacji. Dzięki analizie oddzielamy ze złożonego zjawiska związki istotne od przypadkowych, elementy właściwe od niewłaściwych. Synteza, proces odwrotny do analizy, polega na myślowym łączeniu elementów wydzielonych przez analizę. Analizując problem rozdzielamy go na poszczególne elementy, a tworząc z nich dzięki syntezie nowe całości, gromadzimy dane do jego rozwiązania.” [Z. Putkiewicz, 1964, s. 16]. Stosując się do omówionych wyżej wskazówek, należy przypuszczać, iż przyczynią się one do rozwijania u uczniów umiejętności analizowania problemu, co jest konieczne do osiągnięcia celu, czyli do rozwiązania zagadnienia.
Ponownie odwołując się do rozdziału 2., drugi punkt rozwiązywania zadania problemowego, tzn. „planuj”, można traktować jako odpowiednik fazy „stawiania hipotez”. W tym etapie poszukuje się pomysłu na rozwiązanie. Zgodnie z definicją zadania problemowego nie istnieje gotowy schemat rozwiązania, lecz trzeba go odkryć. Istotna jest więc znajomość metod sprzyjających temu odkryciu. Podobnie jak w poprzednim etapie, konieczna jest umiejętność stawiania właściwych pytań. Jak pisze J. Kozielecki „...Próbuj wykorzystać swoją dotychczasową wiedzę; znajdź zadanie podobne, które rozwiązywałeś w przeszłości, i zbadaj, czy metody jego rozwiązania nie można przenieść do aktualnej sytuacji zadaniowej...” [J. Kozielecki, 1992, s. 111]. Przede wszystkim należy więc postawić sobie pytanie: Czy nie spotkałem się już kiedyś z podobnym zadaniem? Może spotkałem podobne zadanie lecz w innej postaci?
Szukając takiego pokrewnego zadania, warto pamiętać o kolejnej wskazówce:
„zadania rozwiązane wcześniej i zawierające ten sam rodzaj niewiadomej mają pierwszeństwo przed innymi rozwiązanymi wcześniej zadaniami;
udowodnione wcześniej twierdzenia, zawierające ten sam wniosek co twierdzenie, które staramy się udowodnić, mają pierwszeństwo przed innymi udowodnionymi wcześniej twierdzeniami” [A. Góralski, 1980, s. 96].
Istotny jest fakt, by uczniowie mieli świadomość, że poszukując zadania zawierającego ten sam rodzaj niewiadomej, mamy na myśli niewiadomą w sensie pojęciowym (np. wysokość trójkąta), a nie znak graficzny np. h czy x. Jeśli jednak nie uda się znaleźć takiego zadania pokrewnego, należy zastanowić się czy nie można zadania sformułować inaczej, tzn. możliwe, iż przy innej interpretacji okaże się ono łatwiejsze (np. zamiast interpretacji algebraicznej można spróbować (jeśli jest to możliwe) interpretacji geometrycznej itp.).
Kolejna wskazówka heurystyczna brzmi następująco: „Pracuj krokami. Jeśli nie możesz od razu znaleźć rozwiązania, próbuj osiągnąć wynik cząstkowy. Zbiór wyników cząstkowych może doprowadzić cię do celu...” [J. Kozielecki, 1992, s. 111]. Zatem, mając problem z rozwiązaniem zadania, należy spróbować rozwiązać zadanie bardziej ogólne lub szczegółowe, tzn. np. jeśli zadanie dotyczy dowolnego czworokąta, można najpierw przeprowadzić rozważania w szczególnych przypadkach, np. gdy ów czworokąt jest kwadratem lub prostokątem. Wtedy może się okazać, iż rozwiązując taki szczególny przypadek, zauważamy pewne własności, które również są prawdziwe w ogólnym przypadku. Czasami bywa pomocne rozwiązanie zadania przy zachowaniu tylko części warunków, a następnie zastanowienie się jakie dodatkowe informacje i zmiany wnoszą te chwilowo opuszczone warunki.
Ponadto, bardzo istotne jest zapoznanie uczniów z metodami matematyki, czyli rozumowaniem: dedukcyjnym i redukcyjnym (zwłaszcza tym drugim). Dedukcja, tzn. wyciąganie wniosków z założeń stosując odpowiednie twierdzenia i tautologie logiczne, jest rozumowaniem stosunkowo często stosowanym w szkole. Niestety nie można tego powiedzieć o redukcji. Potwierdzają to badania p. Ciosek. Otóż, analizując 250 prac z egzaminów wstępnych na Akademię Pedagogiczną w Krakowie (zatem były to prace osób bardziej zaawansowanych w matematyce) okazało się, iż zaledwie 9 osób stosowało redukcję (czyli rozumowanie, w którym wychodzimy od celu, a następnie „cofamy się” przez warunki wystarczające) i 15 osób korzystało z metody dedukcyjno - redukcyjnej. Jest to ciekawe zjawisko, zważywszy na fakt, iż w życiu codziennym metoda ta jest bardzo często spontanicznie stosowana, np. planujemy wyjazd, czyli stawiamy sobie pewien cel, a następnie zgodnie z zasadami redukcji „cofamy się”, zatem zastanawiamy się, co nam wystarczy by osiągnąć cel, tzn. żeby zrealizować ten wyjazd (np. co należy kupić, ile potrzebuję pieniędzy itp.).
Rozwiązując zadanie matematyczne również bardzo często okazuje się, iż redukcja jest najskuteczniejszą metodą (w szczególności zadania konstrukcyjne są tego potwierdzeniem, gdyż właściwa analiza opiera się właśnie na redukcji). Dlaczego więc uczniowie tak rzadko stosują ten typ rozumowania?
Rozważmy następujący przykład zadania:
Udowodnij, że jeśli a > 0, b > 0 i a =/= b, to:
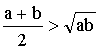
Do rozwiązania takiego zadania warto wykorzystać redukcję, tzn.:

W tym momencie stwierdzamy, że ta nierówność jest prawdziwa, gdyż a =/= b, więc a - b =/= 0, a kwadrat liczby różnej od zera jest zawsze dodatni. Ponieważ wykonując kolejne kroki rozumowania przechodziliśmy przez warunki wystarczające, zatem teraz można „cofnąć się”, tzn. wychodząc od nierówności:
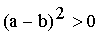
(o której wiemy już, że jest prawdziwa) dojdziemy do tezy twierdzenia, tzn. udowodnimy, że:
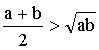
W takim ujęciu rozwiązanie zadania nie powinno sprawiać trudności. Jednak w większości podręczników nie spotyka się takich dowodów, lecz dowody dedukcyjne, tzn. w tym przypadku prezentowane rozumowanie mogłoby rozpocząć się np. od słów:
Wyjdźmy od nierówności, która jest spełniona dla a =/= b:
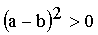
Dalej nastąpiłyby odpowiednie przekształcenia doprowadzające do tezy twierdzenia. Jednak przy tak przedstawionym rozumowaniu zwykle uczeń już na wstępie postawi pytanie: Skąd autor rozwiązania wiedział, że należało wyjść właśnie od takiej nierówności? W konsekwencji uczeń może sobie wyrobić pogląd, że rozwiązywanie zadań, dla których nie ma algorytmu, wymaga wyjątkowej mądrości i dlatego zniechęca się do rozwiązywania. Zwykle nie uświadamia się ucznia, iż autor prezentowanego w podręczniku rozumowania również odkrył je za pomocą redukcji, a następnie przedstawił tylko etap dedukcyjny. Ogromną szkodą jest, iż nie przekazuje się uczniom tej redukcji. Przyczynia się to także do bezradności uczniów przy rozwiązywaniu zadań tekstowych. Często uczeń wypisuje dane, szukane i na tym kończy rozwiązywanie zadania, bowiem korzystając z dedukcji, tzn. wyciągając wnioski z założeń, możemy wysnuć bardzo wiele takich wniosków i niejednokrotnie trudno znaleźć ten właściwy czyli ten, który przybliży nas do rozwiązania. Stosując redukcję, uczeń powinien skupić się na pytaniu (celu zadania), a następnie zastanowić się, co jest wystarczające do rozwiązania, tzn. np. jeśli celem zadania jest obliczyć objętość danej bryły, najpierw trzeba wiedzieć jakie dane są do tego konieczne. Niestety wielu uczniów ma problemy z takim spojrzeniem na zadanie.
Widać więc, iż istotnie wdrażanie uczniów do rozumowania redukcyjnego ma ogromne znaczenie. Można więc sformułować następującą wskazówkę heurystyczną: „Pracuj wstecz: od końca do początku. Załóż, że osiągnąłeś już sytuację końcową (cel), a następnie tak przekształcaj tę sytuację, aby dojść do sytuacji początkowej” [J. Kozielecki, 1992, s. 111].
Mając plan (pomysł) rozwiązania, można przejść do kolejnego etapu, czyli do „wykonania planu” (w ujęciu psychologicznym jest to „weryfikacja hipotez”). Realizując wytworzony we wcześniejszym etapie pomysł, bardzo istotne jest by uczeń sprawdzał poprawność każdego kroku i by umiał go uzasadnić.
W szkole zwykle na tym kończy się rozwiązywanie zadania (ewentualnie formułuje się jeszcze odpowiedź). „Nawet zupełnie dobrzy uczniowie po otrzymaniu rozwiązania zadania i starannym zapisaniu toku rozumowania zamykają książkę i biorą się do czego innego. Postępując tak opuszczają ważną i pouczającą fazę pracy. Spoglądając wstecz na otrzymane rozwiązanie, ponownie rozpatrując i analizując wynik i drogę doń prowadzącą, mogliby utwierdzić swoją wiedzę i rozwinąć swoje zdolności do rozwiązywania zadań. Dobry nauczyciel powinien zrozumieć (i wpoić ten pogląd w swoich uczniów), że żaden problem nigdy nie jest wyczerpany całkowicie. Zawsze coś zostaje jeszcze do zrobienia, badając problem dostatecznie wnikliwie możemy ulepszyć każde rozwiązanie, a w każdym razie zawsze udoskonalić nasze zrozumienie rozwiązania” [G. Polya, 1964, s .34]. Dlatego też, G. Polya dodaje jeszcze jeden etap, tzn. „rzut okiem wstecz”.
Można wyszczególnić trzy główne cele tego etapu. Po pierwsze - sprawdzenie warunków zadania. Wbrew pozorom okazuje się, iż czasami czynność ta może sprawiać uczniom trudności. Otóż, np. rozwiązując zadanie, którego celem jest obliczenie długości krawędzi sześcianu przy określonych warunkach, uczeń układa odpowiednie równanie kwadratowe i rozwiązując je otrzymuje dwa pierwiastki o różnych znakach. Na polecenie: „Sprawdź warunki zadania” - sprawdza czy otrzymane liczby spełniają dane równanie kwadratowe, a następnie przyjmuje je jako rozwiązanie zadania. Nie zastanawia się nad faktem, że jeden z pierwiastków jest ujemny, zaś celem zadania było obliczenie długości krawędzi. Widać więc, iż duże znaczenie ma uświadomienie uczniom, że sprawdzenie warunków zadania polega na konfrontacji otrzymanych wyników z początkowymi realiami zadania (a nie np. z układem równań, który powstał w etapie „układania planu rozwiązania”).
Drugi istotny cel tego etapu, to próba objęcia rozwiązania jednym „rzutem oka”. Dzięki temu, iż po rozwiązaniu zadania, uczeń spróbuje wychwycić najistotniejsze kroki tego rozwiązania, czyli spróbuje uświadomić sobie ogólną ideę, jest szansa, iż w przyszłości spotykając się z podobnym zadaniem, znacznie łatwiej znajdzie rozwiązanie, korzystając z wypracowanej wcześniej metody. Jest to bardzo istotne, bowiem należy pamiętać, iż dając uczniowi do rozwiązania pewne zadanie, naszym celem jest nie tylko rozwiązanie tego jednego konkretnego zadania, lecz rozwijanie umiejętności rozwiązywania wszystkich zadań tego typu i zadań w ogóle.
Trzeci z najważniejszych celów „rzutu okiem wstecz”, to zastanowienie się nad tym, czy można dane zadanie rozwiązać w inny sposób. Jak pisze J. Kozielecki „Obecnie chodzi nie tylko o to, aby rozwiązać problem, ale także o to, aby rozwiązać go jak najszybciej, za pomocą minimalnej ilości informacji, przy najmniejszych kosztach własnych, chodzi o to, aby cena, jaką płacimy za pokonanie trudności, była jak najniższa...” [J. Kozielecki, 1975, s. 11]. „Dlaczego więc w szkole (...) uczniowie raczej zadowalają się stosowaniem mało ekonomicznych strategii, często ściągniętych z podręcznika czy od kolegi? Odpowiedź jest (...) wyjątkowo prosta. (...) męczenie się nad poszukiwaniem lepszych strategii w szkole nie opłaca się. Przecież nauczyciele najczęściej oceniają to, czy uczeń rozwiązał zadanie, a nie to, jak je rozwiązał” [J. Kozielecki, 1975, s. 65]. Potrzebne są więc bodźce, które zachęcą ucznia do takich twórczych poszukiwań. Narzucanie uczniom najlepszego sposobu rozwiązania na zasadzie wiary w autorytet nauczyciela, z pewnością nie jest skuteczną metodą. Jedynie dyskusja różnych rozwiązań umożliwia porównanie ich skuteczności oraz daje odpowiedź na pytanie „co opłaca się najbardziej?”. Tak więc, rozwiązując pewien problem na lekcji, warto poświęcić więcej czasu i wykorzystać wszystkie pomysły uczniów, również te nieskuteczne. Te ostatnie są dobrą okazją do zastanowienia się nad tym, dlaczego nie doprowadziły do osiągnięcia celu, jakie dodatkowe dane umożliwiłyby rozwiązanie zadania tym sposobem. Ponadto, istotna jest refleksja nad możliwością otrzymania różnych wyników przy stosowaniu różnych sposobów rozwiązania (szczególnie dotyczy to zadań, dla których istnieje więcej niż jedno rozwiązanie). Ważność tak obszernej analizy różnych rozwiązań, J.Kozielecki potwierdza słowami: „Próba zredukowania wszystkich dobrych sposobów do jednego, głównie do tego, który stosuje nauczyciel lub który znajduje się w podręczniku, jest z punktu widzenia pedagogiki barbarzyństwem dydaktycznym, jest początkiem niszczenia samodzielności dzieci” [J. Kozielecki, 1975, s. 178-179].
Niewątpliwie realizacja tak sformułowanych postulatów wymaga czasu. Początkowo nauczyciel powinien błądzić wspólnie z uczniem. Jednak nie można cały czas kierować rozwiązywaniem zadań, bowiem wtedy uczymy bezradności. Zatem z czasem, przy doborze odpowiednich zadań, należy pozwolić uczniom samodzielnie błądzić, a tym samym rozwijać umiejętność rozwiązywania problemów.
4. Problem, a aktywizacja procesu myślenia
Mówiąc o aktywizacji ucznia, oczywiście nie chodzi o aktywność fizyczną, tzn. np. częste chodzenie do tablicy. Istotne jest to, co dzieje się w umyśle, tzn. aktywizacja procesów myślowych. Czy zatem zadanie problemowe rzeczywiście jest czynnikiem aktywizującym ucznia?
Z. Krygowska w trzeciej części „Zarysu dydaktyki” opisuje różne postawy uczniów. Pierwsza, to postawa uczennicy, która po zapoznaniu się z algorytmem rozwiązywania układów dwóch równań liniowych o 2 niewiadomych metodą tzw. „podstawiania”, dobrowolnie rozwiązała w domu 100(!) takich układów, różniących się jedynie współczynnikami. Drugi przykład, to postawa ucznia, który miał za zadanie przedstawić liczbę 17 na różne sposoby (np. 17 = 10 + 7, 17 = 20 - 3, 17 = 5 • 4 - 3, 17 = (100 - 20) : 4 + 2 - (10 : 2) itp.). Chłopak tak zafascynował się poszukiwaniem różnych przedstawień, iż nie chciał przerwać swej działalności mimo późnej pory. Wreszcie, po zapisaniu liczby 17 na wiele sposobów, zaczął uświadamiać sobie, iż nierealne jest wyczerpanie wszystkich możliwości.
Mimo pozornej aktywności zarówno uczennicy jak i ucznia, okazuje się, iż jedynie w tym drugim przypadku możemy mówić o aktywizacji procesów myślowych. Uczennica powtarzała automatycznie tę samą czynność, która nie wymagała od niej większego wysiłku intelektualnego. W trakcie rozwiązywania zadania problemowego, taka sytuacja jest niemożliwa, gdyż „...Tylko dzięki zaktywizowaniu wiedzy już posiadanej uczeń może zrozumieć problem, określić oraz wyszukać potrzebne do jego rozwiązania dane, wskazać wchodzące w grę związki i zależności, a następnie - uporać się z nim” [Cz. Kupisiewicz, 1973, s. 35]. Również Z. Putkiewicz potwierdza fakt, iż zadanie problemowe jest silnym bodźcem aktywizującym procesy myślowe: „Chcąc, żeby uczeń zaczął myśleć, trzeba postawić mu nowe zadanie, zawierające określoną trudność, którą trzeba pokonać, aby zadanie rozwiązać. Rozwiązując je będzie starał się wykorzystać nabyte wcześniej wiadomości w zastosowaniu do nowych warunków, będzie również analizował sytuację, porównywał fakty, szukał związków, wnioskował, formułował sądy, dowodził i uzasadniał” [Z. Putkiewicz, 1964, s. 13]. Dążąc do aktywizacji ucznia, należy więc dostarczać mu zadań, w których wymagania będą nieco wyższe od górnej granicy jego możliwości. Wtedy „...nie wystarczy stosowanie znanych schematów, gdyż problem trzeba przeanalizować, aby móc go rozwiązać. Szereg elementów jest uczniowi znanych, ale połączenia są inne, wobec tego i wynik końcowy będzie inny. Znalezienie wyniku końcowego wymaga wielu operacji, które w tych warunkach doprowadzą do pożądanego efektu” [Z. Putkiewicz, 1964, s .28].
Ucząc matematyki nie można ograniczać się jedynie do realizacji najniższego celu, tzn. do przekazania określonych treści matematycznych. Bardzo istotne jest wyrobienie u uczniów postaw, które będą przydatne w różnych dziedzinach życia. Nauczanie problemowe umożliwia realizację tego celu, gdyż jak pisze o nim Cz. Kupisiewicz - „...przyczynia się (...) do wdrażania uczniów do samokształcenia. Wyrabiając w uczniach umiejętność dostrzegania i rozwiązywania problemów oraz sprawdzania uzyskiwanych rezultatów, przyzwyczaja ich do samodzielności i posługiwania się właściwą techniką pracy umysłowej, co jest warunkiem wydatnej pracy samokształceniowej” [Cz. Kupisiewicz, 1973, s. 220]. Również zdaniem J. Kozieleckiego „Nauczanie problemowe jest rzeczywiście metodą, która uaktywnia młodzież, (...) jest pigułką przeciw nudzie, na brak której w tradycyjnej szkole nie mogliśmy narzekać” [J. Kozielecki, 1975, s. 181-182].
Fakt, iż problem jest czynnikiem aktywizującym procesy myślowe, wynika również bezpośrednio z teorii Piageta. Otóż, każdy człowiek posiada wiedzę zakodowaną w pewne schematy. Piaget odwołuje się do nadrzędnych praw natury, zgodnie z którymi wszystkie organizmy dążą do równowagi. Zatem, gdy napotykamy zdarzenia, które są nowe lub nie pasują do istniejących struktur wiedzy, następuje zachwianie owej równowagi. Wtedy podejmowana jest próba asymilacji. „Czynność asymilacji rozpoczyna się w momencie, gdy organizm napotyka nowe zdarzenie (bodźce), które potencjalnie może zostać przyswojone i włączone w obręb już istniejących struktur wiedzy, w jakiś sposób odpowiednich dla niektórych lub wszystkich elementów tego nowego zdarzenia” [Galloway, 1988, s. 103]. Zdaniem Piageta organizm odbiera ze środowiska tylko te bodźce, które potencjalnie wiążą się z posiadaną już strukturą wiedzy. Wtedy „...jeśli istnieją stosowne wstępne struktury, nowe bodźce ulegają zasymilowaniu, zostają przyswojone i włączone w obręb tych struktur” [Galloway, 1988, s. 103-104]. Istotny jest fakt, iż ze względu na to, że różne organizmy mogą posiadać inne struktury wiedzy wyjściowej, każdy uczący sam przypisuje znaczenie asymilowanym bodźcom, więc nie jest to cecha obiektywna.
Druga składowa procesu poznawczego, (tzn. zachowania adaptacyjnego) to akomodacja. Pojęciem tym Piaget określa to, co dzieje się w procesie asymilacji z już istniejącymi strukturami wiedzy. Otóż, „Nowa informacja nie jest ot tak, po prostu, wprowadzana i dołączana do tych struktur. To raczej istniejące struktury „akomodują się” tzn. dostosowują się, adaptują - do asymilowanej informacji. Rezultatem akomodacji jest zmodyfikowana struktura wiedzy, a zatem i nowy poziom poznania. Właśnie na tym polega podstawowe działanie w procesie rozwoju” [Galloway, 1988, s. 104]. Widać więc, iż zdaniem Piageta proces poznawania, to proces adaptacji, który dokonuje się za pośrednictwem równoważnych wewnętrznie czynności - asymilacji i akomodacji. [Galloway, 1988]. Zatem, istotnie zakłócanie równowagi schematu (tzn. stwarzanie sytuacji problemowych i podejmowanie prób rozwiązania sformułowanych na ich tle problemów) jest głównym czynnikiem rozwoju.
Zdaniem S.Garczyńskiego, „Informacja, która nas bawi, wzrusza, gniewa lub martwi natychmiast się w nas zadamawia. Więcej! Pobudza do umysłowej aktywności, która wspaniale pamięci sprzyja” [S. Garczyński, 1976]. Zadanie problemowe jest właśnie informacją tego typu, gdyż w pewien sposób „martwi ucznia” (tzn. dając uczniowi do rozwiązania zadanie problemowe, stawiamy przed nim trudność, której nie można łatwo natychmiast pokonać). Jest więc nadzieja, iż wiadomości zdobyte w sposób problemowy, pozostaną na dłużej w pamięci ucznia. Należy jednak pamiętać, iż ważne są nie tylko konkretne treści matematyczne, ale również postawy, które wyrabiamy u ucznia ucząc go rozwiązywania problemów: umiejętność aktywnego podchodzenia do problemu, wnioskowanie, racjonalne planowanie, logiczne myślenie itp. Stawiajmy więc ucznia jak najczęściej w sytuacjach problemowych, gdyż „...wartość szkolnej nauki sprowadza się do tego, co w byłym uczniu pozostanie, gdy zapomni, czego się w szkole nauczył...” [S. Garczyński, 1976].
|