OpTyKa

Optyka, to nie tylko proste obrazowanie przedmiotów na podstawie biegu promieni przyosiowych. Fala niesie przecież energię, ma swoją częstość i fazę, które to wielkości oddziaływują z urządzeniami na swojej drodze.

Poniższe rozważania można uogólnić także na inne rodzaje fal, takie jak promienie X, mikrofale czy nawet fale dźwiękowe.

Aby w inny sposób opisać działanie np. soczewki wprowadźmy pojęcie matched filter, które jak się okaże jest optymalnym liniowym detektorem dla znanego sygnału. Uogólnimy w ten sposób problem działania soczewek na inne dziedziny.

Rozpatrzmy pewien sygnał
i jego transformację Fouriera
przechodzący przez liniowy filtr dający pewną czasową odpowiedź
lub w funkcji częstości
. Na wyjściu takiego filtra otrzymujemy odpowiedź
, która też jest transformatą Fouriera sygnału wyjściowego.

co daje po policzeniu transformaty odwrotnej splot funkcji czasowych

gdzie granice całki są czasem w którym sygnał dociera do filtra.

Ponieważ odbierany sygnał jest proporcjonalny do kwadratu wielkości opisującej daną falę i przy zastosowaniu nierówności Couchego-Schwarza otrzymujemy

Przebadajmy te równanie zakładając że,
dla ustalonego A.

Filtr dostarczy nam maksymalnego sygnału, gdy sygnał jaki otrzymamy na wyjściu jest równy co do wartości, ale sprzężony do sygnału biegnącego odwrotnie w czasie. Taki układ nazywamy filtrem dopasowanym i służy do detekcji sygnałów o znanym przebiegu czasowym jak np. sygnał echa radaru.

Aby zrozumieć co ma wspólnego dopasowany filtr z soczewkami rozważmy następujący model soczewki:

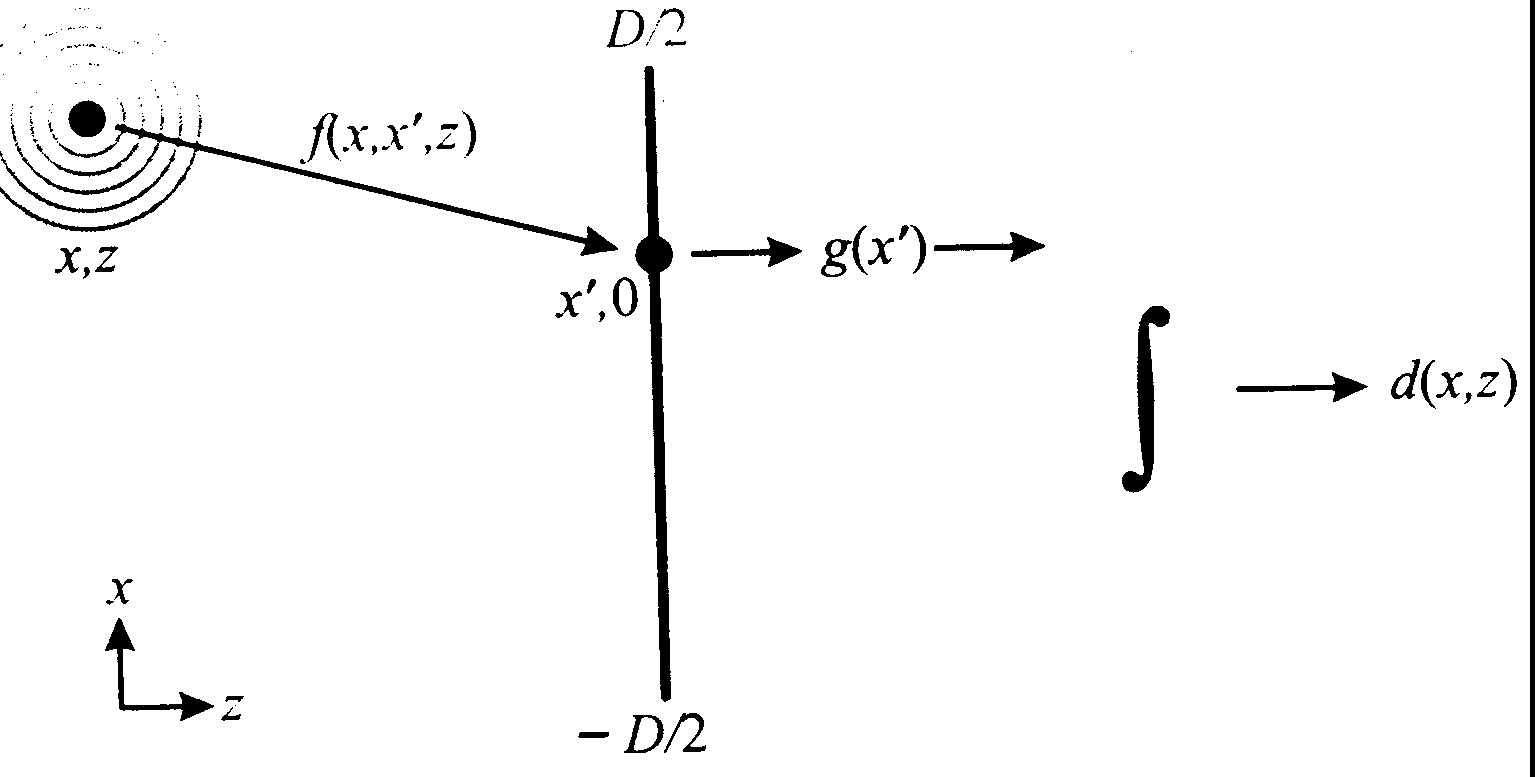
Zmianę amplitudy fali otrzymamy mnożąc falę przez zespolony czynnik zależny od drogi, którą musi przebyć fala
. Sygnał, który otrzymamy w pewnej odległości od soczewki będzie zależny od całki po całej jej powierzchni pomnożonej przez pewien czynnik
uwzględniający zmianę fazy w soczewce i drogę do detektora. Dodatkowo oznaczmy przez
faktor określający szansę detekcji amplitudy i fazy sygnału w płaszczyźnie detektora.

Załóżmy ponownie, że rozpatrujemy tylko promienie przyosiowe
, ponadto pomińmy czynnik
ponieważ interesuje nas tylko składowa prostopadła f od x. Odpowiedź detektora wyniesie więc

czyli jest to splot funkcji, a więc aby odpowiedź detektora była maksymalna

Dla źródła na osi optycznej redukuje się to do

Dopasowana soczewka powinna więc mieć kwadratową zależność fazy od odległości od osi optycznej.

Zobaczmy jak soczewka odpowiada na sygnał którego źródło nie leży na osi optycznej. (x,z) zamiast (0,z)

gdzie
. Dla
wynik dąży do funkcji delta.

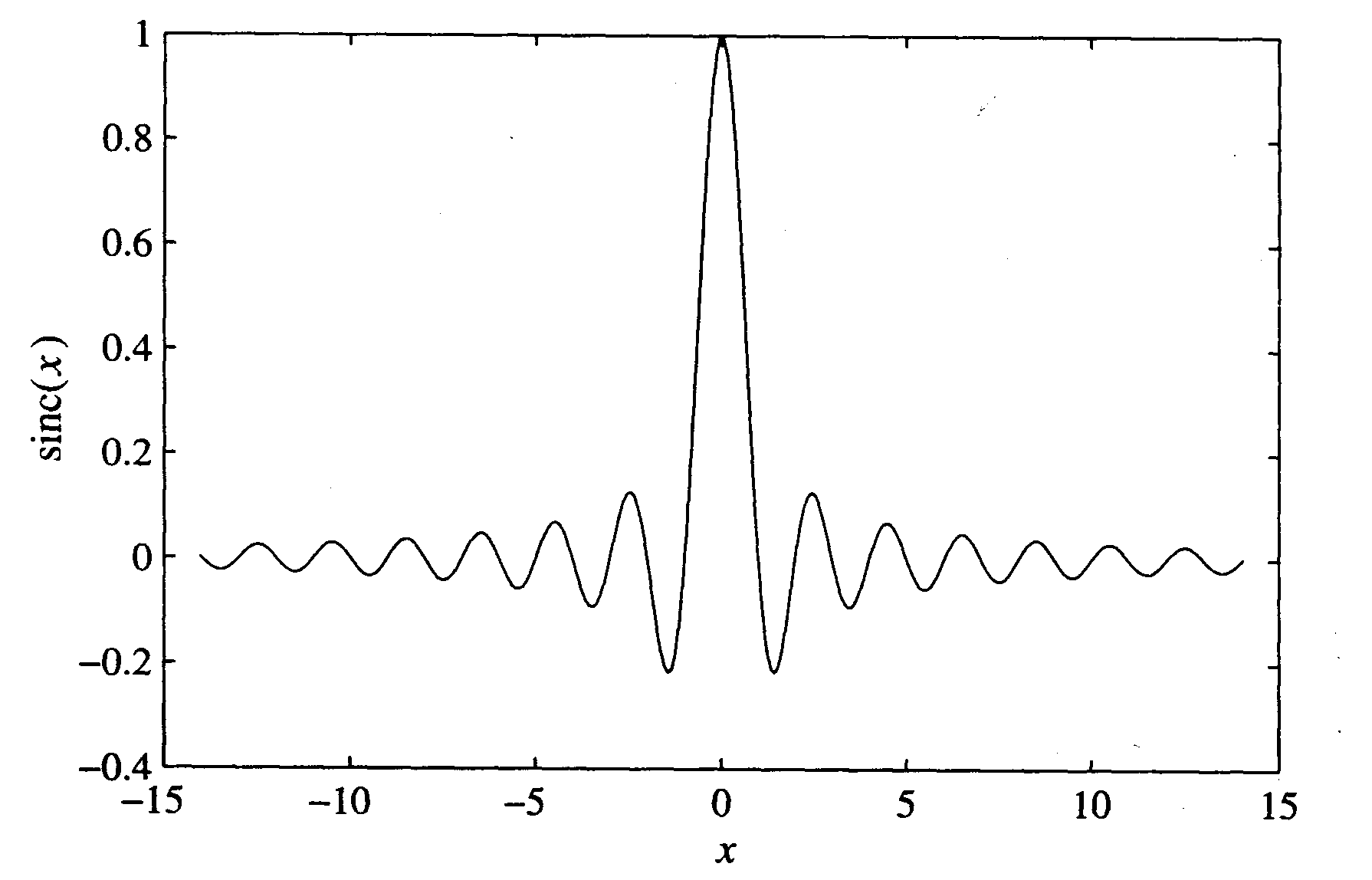
Matched filters mogą być układem (matrycą) kanałów przewodzących i odbiorników. Można sterując odpowiednio wysyłanym sygnałem testować położenie wybranego obiektu. Sa to teoretyczne podstawy pracy radarów matrycowych. Jednocześnie w wypadku soczewki widać jak jej apertura D wpływa na zdolność rozdzielczą. Aperturę soczewek ograniczają np. rozmiary satelity, ale poruszający się nadajnik i odbiornik mogą pracować jak Matched filter jeżeli będziemy w odpowiedni sposób sterować sygnałem. Na tej zasadzie pracują radary na satelitach, których zadaniem jest tworzenie mapy Ziemi.

Obrazowanie koherentne

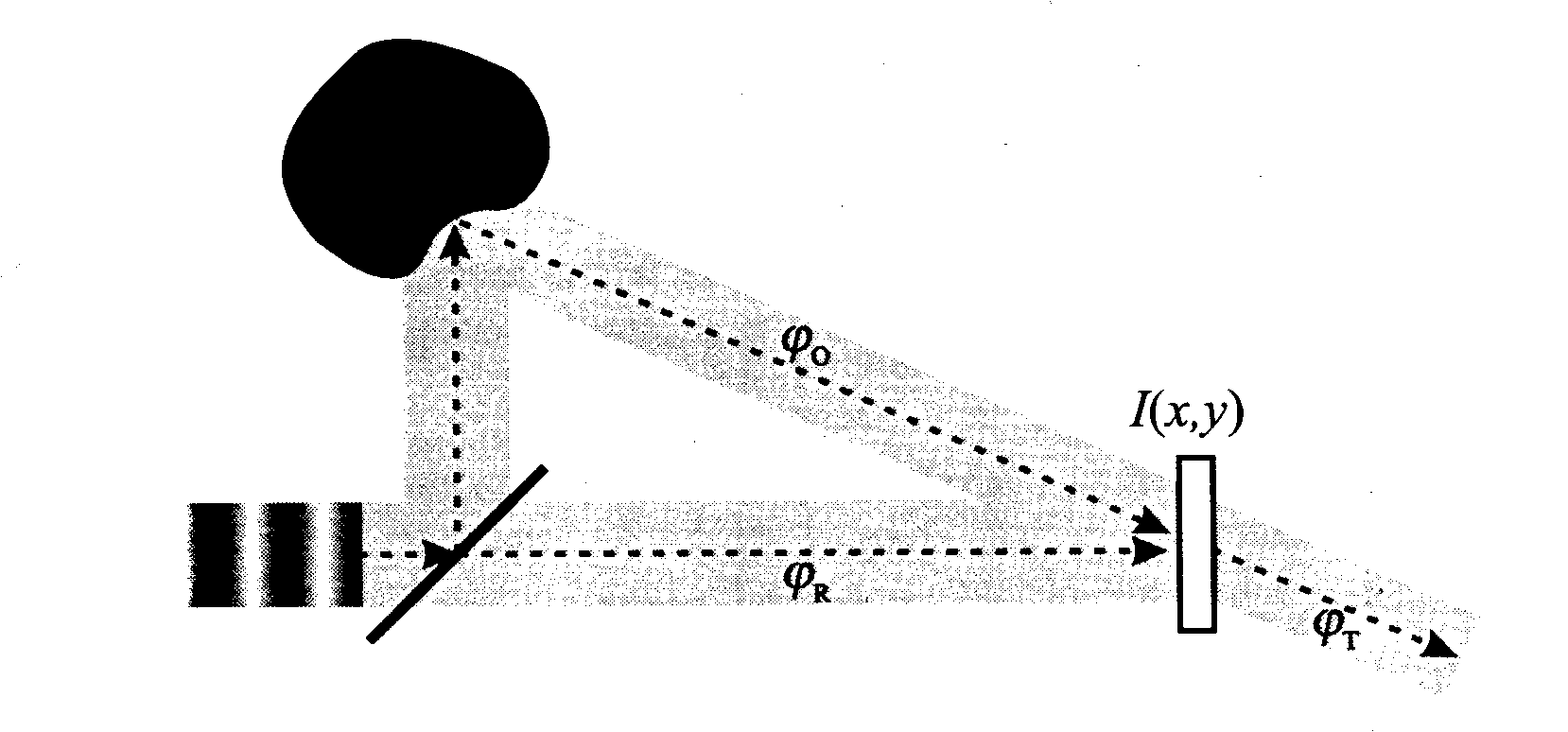
Powyższe rozważania oparte były na koherentności promieniowania, a więc możliwości zajścia interferencji bez względu na odległość przebywaną przez promień. Większość detektorów to jednak detektory reagujące na kwadrat natężenia fali. Gubią więc one informacje o fazie fali Ta ostatnia może być jednak zapisana przy pomocy techniki nazywanej holografią.

Rozważmy oświetlenie przedmiotu falą koherentną, której część pada bezpośrednio na detektor (kliszę światłoczułą). Promień odbity od przedmiotu i tzw. fala odniesienia interferują w płaszczyźnie naszego detektora:

zarejestrowane natężenie wyniesie więc:

Jeżeli przez kliszę o rozkładzie natężenia podanym powyżej przepuścimy falę

otrzymamy

czyli pierwszy człon otrzymanej fali będzie taki sam jak fali biegnącej od obiektu. Przez hologram widać przedmiot przestrzennie i można na niego spoglądać z różnych stron, a ograniczeniem jest jedynie wielkość kliszy. Pozostałe człony wytwarzanej fali wprowadzają do obrazu pewne zakłócenie, jednak mogą być eliminowane poprzez odpowiedni układ geometrii w trakcie wykonywania hologramu.

Okazuje się, że hologramy można otrzymywać także syntetycznie. Układ prążków można obliczyć numerycznie następnie powiększony obraz wydrukować i sfotografować. Jeszcze ciekawsza metoda to otrzymywanie obrazów holograficznych w czasie realnym przy użyciu akustyczno-optycznych modulatorów.

Hologramy mogą skutecznie zastępować rzeczywiste elementy optyczne. Syntetyczny hologram może działać jak soczewka, siatka dyfrakcyjna lub inne elementy. Cienka klisza może transformować promień lasera w sposób nieosiągalny dla klasycznej optyki. (Holographic Optical Elements HOEs).

Rzeczywiste światło nie jest oczywiście idealnie koherentne. Zależność od częstości można w przybliżać rozkładem Gaussa o szerokości
. Czasowa zależność sygnału jest też Gaussowska o szerokości
ponieważ transformata Fouriera rozkładu Gaussowskiego jest też rozkładem Gaussowskim o wariancji będącej odwrotnością wariancji pierwotnej.:

(nieoznaczoność częstotliwościowo - czasowa)

Z czasem koherencji powiązana jest wielkość nazywana drogą koherencji będącą największą różnicą dróg dla których promienie jeszcze interferują
. Jeżeli hologram oświetlany jest wiązką o szerokim paśmie częstości poszczególne fale interferują i rozpraszają się pod różnymi kątami powodując rozmywanie się obrazu. Różne kolory światła tworzą obrazy w różnych nie pokrywających się miejscach.

Inne zastosowania holografii:

Optyczna Tomografia - Opical Coherence Tomography OCT

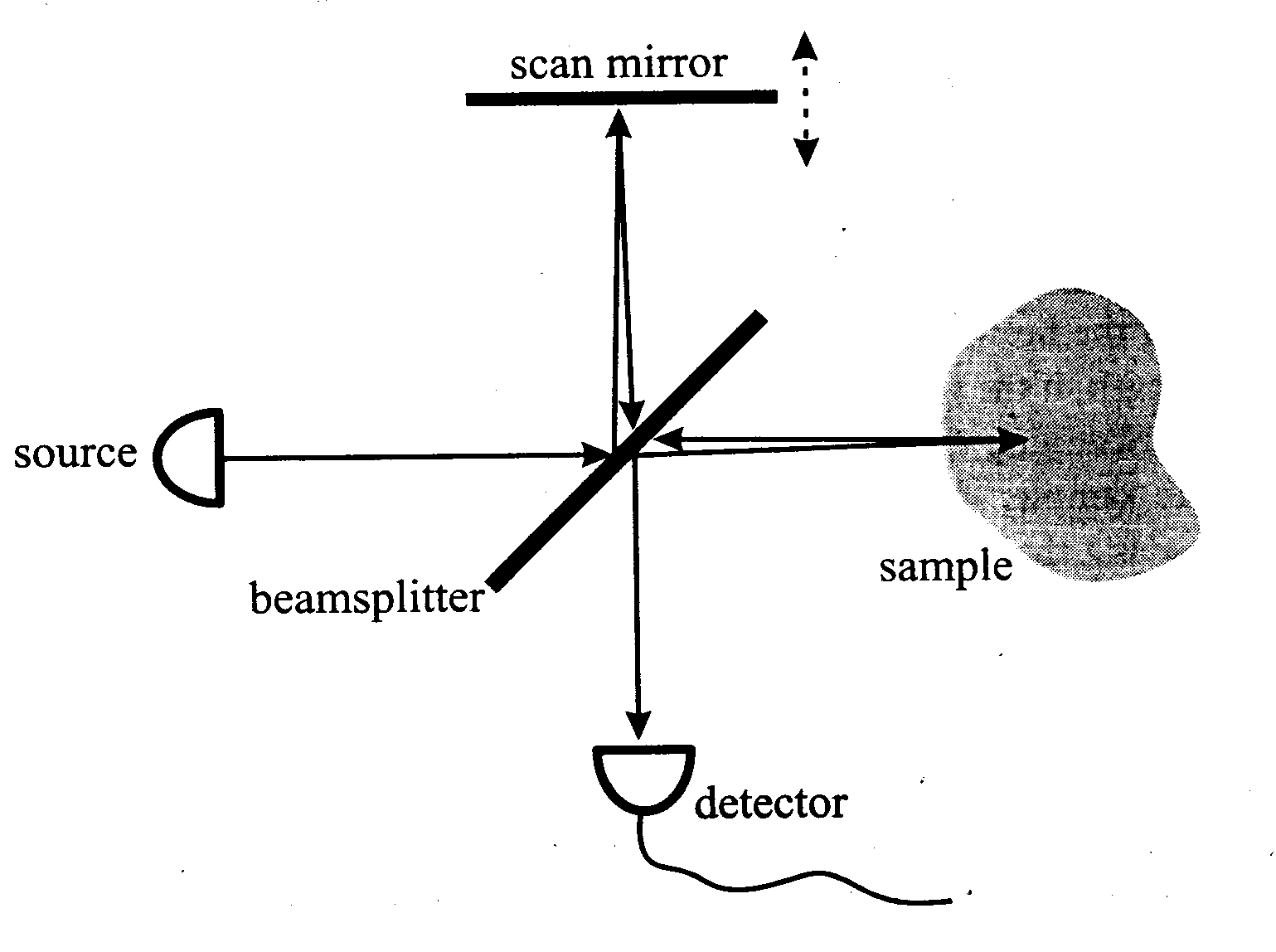
Interferometria Holograficzna - dwuekspozycyjna holografia.

Tomografia Komputerowa

OCT posiada pewne ograniczenia - promień nie może rozpraszać się na przedmiocie wiele razy gdyż prowadzi to do degradacji obrazu (informacja jest zbyt skomplikowana by była użyteczna w dalszych obliczeniach)

Inna sytuacje występuje gdy jako promieniowanie użyjemy promieni X. Większość fotonów porusza się przez materiał po liniach prostych lub zostaje zaabsorbowana. Pomiary tej absorpcji w zależności od orientacji próbki pozwalają badać wewnętrzną strukturę. Metoda ta nazywa się tomografią komputerową. (Computed Tomography CT, Computerized Axial Tomography, Computer-Assisted Tomography).

Załóżmy, że mamy próbkę oświetloną falą płaską tworzącą z osią x kat θ. Niech ρ(x,y) będzie rozkładem współczynnika absorpcji w dwuwymiarowej próbce.

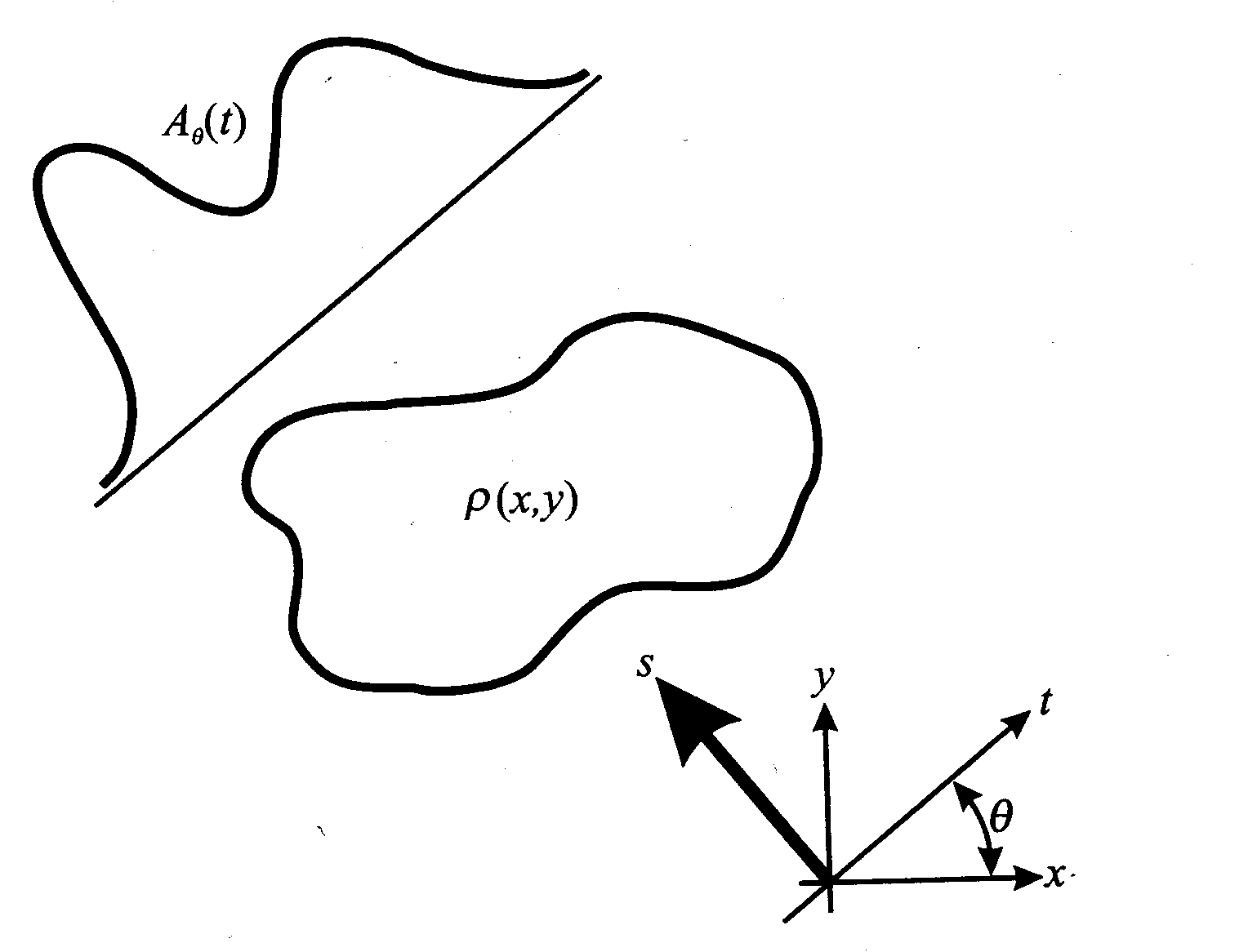
Całkowita absorpcja w tym kierunku zależy od drogi pokonywanej przez wiązkę:

Jest to tak zwana transformata Randona.

Rozważmy teraz przestrzenną transformatę Fouriera współczynnika absorpcji.

Czyli przestrzenna transformata Fouriera z całkowitej absorpcji w danym kierunku daje możliwość odtworzenia lokalnego współczynnika absorpcji. Wystarczy wykonać teraz pomiary w różnych kierunkach aby odtworzyć całkowitą przestrzenną absorpcję.

Rezonans magnetyczny MRI

Rezonans magnetyczny oparty jest na zjawisku NMR Nuclear Magnetic Resonance. Aby nie brzmiało to nieco przerażająco zmieniono nieco nazwę. Tym bardziej, ze potrzebne energie są ~10^-13 razy mniejsze od tych potrzebnych do przeprowadzenia reakcji jądrowej.

Wiele cząstek elementarnych posiada wewnętrzny moment magnetyczny μ związany z wewnętrznym momentem pędu J. Te dwie wielkości powiązane są współczynnikiem żyromagnetycznym γ.

Cząsteczki zachowują się jakby wirowały i są dipolami magnetycznymi. Tę ich właściwość nazywamy spinem choć nie wirują one w klasycznym sensie. Zewnętrzne pole magnetyczne reaguje z wewnętrznym momentem magnetycznym wywołując moment siły
co z kolei powoduje zmianę momentu pędu i momentu magnetycznego,

co powoduje precesję momentu pędu wokół pola magnetycznego z częstością
.

Przeprowadźmy semiklasyczne przybliżenie tej sytuacji. Rozważmy cząstkę o ładunku g krążącą po orbicie o promieniu r z okresem T. Obliczmy kolejno moment pędu tej cząsteczki, prąd, który ona wywołuje i związany z tym prądem moment magnetyczny:

Brak zależności od r sugeruje, że ten związek może być ogólniejszym.

Odwrotna zależność od masy prowadzi do dużego zróżnicowania częstości precesji.

W doświadczeniu NMR silne pole przyłożone do próbki powoduje precesje momentów magnetycznych - zmienne pola magnetyczne, tym silniejsze im więcej jest spinów określonego rodzaju. Powoduje to generowanie sygnału w cewce odbiorczej. Aby jeszcze dodatkowo określić położenie danych spinów wywołuje się ściśle określony gradient pola stałego pola magnetycznego...

Dokończenie wkrótce

---