1. Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się z procesem wytwarzania obrazów przez soczewki cienkie oraz z metodami wyznaczania odległości ogniskowych soczewek cienkich.

2. Wprowadzenie teoretyczne.

Wiązka promieni, posiadająca jeden wspólny punkt przecięcia, nazywa się wiązką hemocentryczną. Może ona być wiązką rozbieżną lub zbieżną. Zadaniem układu optycznego jest przekształcanie każdej wiązki hemocentrycznej w inną, również hemocentryczną. Będziemy rozpatrywali tylko układy składające się z powierzchni sferycznych. Osią optyczną takiego układu będzie prosta, na której znajdują się środki krzywizn tych powierzchni.

Każdy przedmiot będziemy traktowali jako zbiór punktów wysyłających promieniowanie. Obrazem takiego przedmiotu będzie również zbiór punktów, do których schodzą się hemocentryczne wiązki promieni.

Zbiór punktów przestrzeni, w której znajdują się przedmioty, nazywamy przestrzenną przedmiotową, a zbiór obrazów punktów przestrzeni przedmiotowej tworzy przestrzeń obrazową.

Rozróżniamy przedmioty rzeczywiste i urojone oraz obrazy rzeczywiste i urojone. Z przedmiotu rzeczywistego z każdego jego punktu jest wysyłana wiązka rozbieżna promieni. Takie rozbieżne hemocentryczne wiązki promieni będą padały na rozpatrywany element optyczny. W przypadku przedmiotu urojonego na element optyczny będzie padała zbieżna wiązka promieni.

Soczewką nazywamy bryłę z materiału przezroczystego, ograniczoną z dwóch stron powierzchniami sferycznymi (jedna z nich może być płaska).

Środkami krzywizny O₁, O₂ soczewki nazywamy środki kul, których częściami są powierzchnie łamiące soczewki, a promieniami krzywizn r₁, r₂ soczewek promienne tych kul.

Osią optyczną nazywamy prostą przechodzącą przez środki krzywizn obu powierzchni soczewki. Odległość między wierzchołkami C₁, C₂ obydwu powierzchni soczewek jest jej grubością d.

Soczewkę nazywamy cienką, jeśli jej grubość d można zaniedbać w porównaniu z powierzchniami krzywizn powierzchni. Dla soczewek cienkich można przyjąć, że punkty C₁ i C₂ pokrywają się ze środkiem ich grubość, do którego należy liczyć odległości s i s' punkt C nazywa się środkiem optycznym soczewki.

Wzór wiążący odległość przedmiotu s oraz obrazu s' od soczewki cienkiej ma postać:

gdzie:

r1,r2 - promienie krzywizny pierwszej i drugiej powierzchni łamiącej soczewki,

n - współczynnik załamania materiału soczewki,

n' - współczynnik załamania ośrodka, w którym znajduje się soczewka.

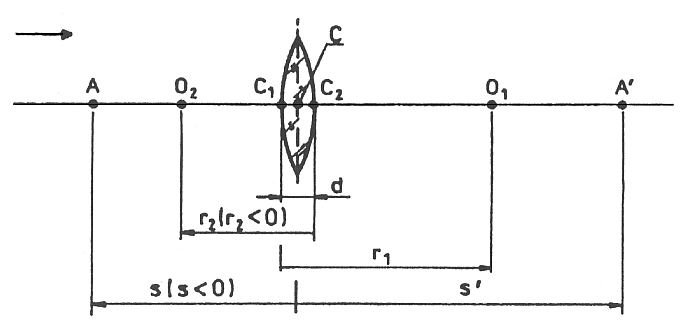
Rys.1 Soczewka skupiająca.

Ogniskiem obrazowym F' nazywamy punkt, w którym skupiają się promienie przyosiowe równoległe do osi optycznej soczewki po przejściu przez nią lub wsteczne przedłużenia tych promieni.

Ogniskiem przedmiotowym F soczewki jest punkt którego obraz znajduje się w nieskończoności.

Soczewka skupiająca to taka , której ogniska F' i F są rzeczywiste, tzn. że w nich skupiają się promienie równoległe do osi optycznej po przejściu przez tę soczewkę. Dla soczewek skupiających f'> 0.

Soczewka rozpraszająca to taka, której ogniska F' i F są urojone (pozorne), tzn. że w nich skupiają się przedłużenia promieni równoległych do osi optycznej po przejściu przez tę soczewkę. Dla soczewek rozpraszających f'< 0.

3. Układy pomiarowe.

• Wyznaczenie odległości ogniskowej soczewek skupiających metodą Bessela.

Jak wynika ze wzoru soczewkowego, wielkości s i s' wchodzą do wzoru symetrycznie. Zatem dla tej samej odległości przedmiotu i ekranu można znaleźć dwa położenia soczewki, dla których otrzymujemy na ekranie ostry obraz - raz pomniejszony, drugi raz powiększony. Oba położenia soczewki są symetryczne względem przedmiotu i ekranu. Jeśli odległość przedmiotu od ekranu oznaczymy przez d, a odległość między obu położeniami soczewek przez c, to jak wynika z rys.2,

,

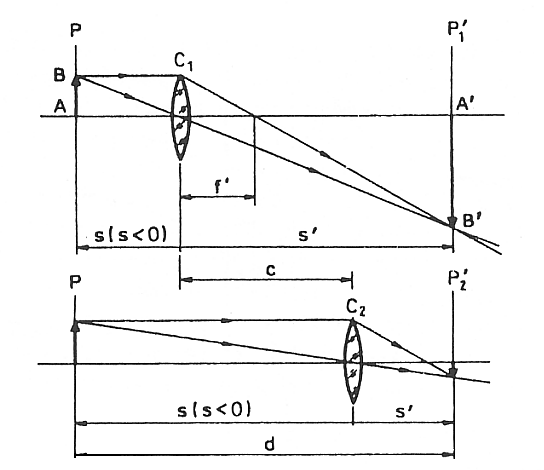
Rys.2 Wyznaczanie odległości ogniskowej soczewki skupiającej metodą Bessela.

AB - przedmiot, A'B' - obraz, f' - ogniskowa obrazowa soczewki, C₁ i C₂ - pierwsze i drugie położenie soczewki, c - odległość między tymi położeniami, d - odległość między przedmiotem a ekranem.

Po podstawieniu wartości s i s' do wzoru soczewkowego otrzymujemy:

Ponieważ
, więc metoda Bessela daje się zastosować tylko wtedy, gdy d>4f'.

Metoda Bessela jest jedną z najdokładniejszych metod. Wyższość tej metody polega na tym, że odległość d i c są tylko pośrednio związane z odległościami s i s'. W przypadku menisków lub soczewek grubych odległość s i s' należałoby mierzyć od tzw. Płaszczyzn głównych soczewek, których położeń tutaj wyznaczyć nie potrafimy. W metodzie Bessela trudność tą omijamy, gdyż przez pomiar c, jako różnicy dwóch położeń soczewki, błędy wynikłe z nieznajomości położenia płaszczyzn głównych są małe.

Metodę Bessela można również zastosować do wyznaczenia odległości ogniskowej soczewek rozpraszających. W tym celu badaną soczewkę należy złożyć razem z soczewką skupiającą o znanej ogniskowej obrazowej f'₂ dobranej, aby otrzymany układ soczewek był skupiający (dodatni), a jego ogniskowa 4f'_1,2<d.

Odległość ogniskową f'2 soczewki rozpraszającej wyznaczymy z zależności dla układu dwu soczewek złożonych razem.

gdzie:

f'₁ - odległość ogniskowa obrazowa soczewki skupiającej, f'₂ - odległość ogniskowa obrazowa soczewki rozpraszającej, f'_1,2 - odległość ogniskowa obrazowa układu soczewek. Ogniskową f'_1,2 wyznaczamy metodą Bessela przez włożenie obydwu soczewek do wspólnej oprawy.

• Wyznaczanie odległości ogniskowych soczewek za pomocą okularu mikrometrycznego i kolimatora.

Kolimator składa się z obiektywu O_k o ogniskowej f_k, w której płaszczyźnie ogniskowej umieszcza się płytkę P_m (zwaną płytką ognistą) z naciętą na niej podziałką. Za kolimatorem umieszczamy na ławie optycznej badaną soczewkę skupiającą S (lub skupiający układ soczewek), której odległość ogniskową należy wyznaczyć (rys.3a). Promienie wychodzące z dowolnego punktu A podziałki płytki ogniskowej kolimatora, odległego od osi optycznej układu o x są po wyjściu z obiektywu kolimatora wzajemnie równoległe i tworzą w płaszczyźnie ogniskowej badanej soczewki obraz A' tego punktu w odległości x' od osi. Jak widać na rysunku, z podobieństwa odpowiednich trójkątów wynika oczywista zależność.

skąd

przy czym α jest kątem, jaki tworzy promień wychodzący z punktu a na skali kolimatora z osią optyczną układu. Ogólniej, ze znikomo małym błędem można przyjąć x za odległość dwóch dowolnych punktów skali kolimatora, a x' - za odległość ich obrazów.

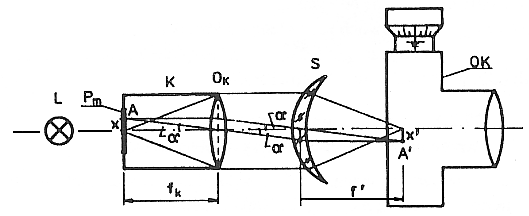
Rys.3 Zasada pomiaru odległości ogniskowej soczewki metodą kolimatora i okularu mikrometrycznego: a - schemat biegu promieni: L - oświetlacz, P_m - płytka ogniskowa z podziałką, K - kolimator, Ok. - obiektyw kolimatora, f_k - ogniskowa przedmiotowa obiektywu kolimatora, S - badana soczewka, f' - ogniskowa obrazowa badanej soczewki, A' - obraz punktu A, Ok - okular mikrometryczny,

W celu zwiększenia dokładności pomiaru f' należy mierzyć długość x między odległymi od siebie kreskami. Jeśli mierzona odległość między kreskami wynosi k numerowanych działek skali, a odległość kątowa między kolejnymi numerowanymi kreskami skali wynosi α₀ , to
. Wartość α₀ podano w instrukcji znajdującej się na stanowisku pomiarowym. Wartość działki elementarnej bębna śruby okularu mikrometrycznego wynosi 0,01mm. Liczbę pełnych obrotów śruby można wyznaczyć podczas obserwacji przesuwu dwóch równoległych kresek na tle skali w polu widzenia okularu mikrometrycznego. Odległość między numerowanymi kreskami tej skali odpowiada jednemu obrotowi śruby.

4. Tabele pomiarowe, przykładowe obliczenia.

• Metoda Bessela.

Dla soczewki 1:

d = 45 cm f'= 10cm

Lp.	C1	C2	C	ΔC
	[cm]	[cm]	[cm]	[cm]
1	110,4	71	39,1	0,2
2	110,5	71,1	39,45	0,2
Średnia	110,45	71,05	39,4	0,2

C₁ - obraz ostry pomniejszony,

C₂ - obraz ostry powiększony

s₁ = 32,7 cm s₂ = 13 cm

s'₁ = s₁ + d s'₂ = s₂ + d

s'₁ = 32,7 + 45 = 77,7 cm s'₂ = 13 + 45 = 58 cm

C = C₁ - C₂

C = 110,4 - 71 = 39,4 cm

d = 120cm

Lp.	C1	C2	C	ΔC
	[cm]	[cm]	[cm]	[cm]
1	340,6	141,2	199,4	0,2
2	340,8	141,4	199,4	0,2
Średnia	340,7	141,3	199,4	0,2

s₁ = 110,3 cm s₂ = 10,6 cm

s'₁ = s₁ + d s'₂ = s₂ + d

s'₁ = 110,3+ 120 = 230,3 cm s'₂ = 10,6 + 120 = 130,6 cm

C = C₁ - C₂

C = 340,6 -141,2= 199.4 cm

Dla układu soczewek (soczewka 1 i 8).

d = 50 cm, f' = 11cm

Lp.	C1	C2	C	ΔC
	[cm]	[cm]	[cm]	[cm]
1	123,2	82,4	40,8	0,2
2	123,2	82,2	41	0,2
Średnia	123,2	82,3	40,9	0,2

s₁ = 36,6 cm s₂ = 16,2 cm

s'₁ = s₁ + d s'₂ = s₂ + d

s'₁ = 36,6 + 50 = 86,6 cm s'₂ = 16,2 + 50 = 66,2 cm

C = C₁ - C₂

C = 123,2 - 82,4 = 40,8 cm

• Metoda okularu mikrometrycznego i kolimatora.

Dla soczewki 1.

zakres	k	x`	α0	f'
skali		[mm]	[ ^o]	[cm]
1/3	20	2,41	4,3	0,016
2/3	30	3,59	4,3	-0,290
całej	6	7,01	4,3	1,451

k = 40 - 20 = 20

x` = 2,87 - 0,46 = 2,41 mm

α₀ = 4,3^o

Dla układu soczewek.

zakres	k	x`	α0	f'
skali		[mm]	[ ^o]	[cm]
1/3	20	2,88	4,3	0,201
2/3	30	4,34	4,3	-0,351
całej	6	8,45	4,3	1,479

K = 40 - 20 = 20

x` =3,04 - 0,16 = 2,88 mm

α₀ = 4,3^o

5. Wnioski.

W ćwiczeniu wykorzystywaliśmy dwie soczewki jedna była soczewką skupiającą , druga rozpraszającą. Pomiary metodą Bessela i metodą okularu mikrometrycznego oraz kolimatora obejmowały pomiar dla soczewki skupiającej oraz dla układu dwóch soczewek złożonych razem jako jedna soczewka. Z wykonanych podczas ćwiczenia trzech metod pomiaru odległości ogniskowych za najdokładniejszą metodę należy uważać metodę Bessela . Bardziej dokładne pomiary można dokonać poprzez zwiększenie ilości pomiarów dla każdej soczewki. Błędy wynikające są spowodowane złym odczytem z przyrządów.

1

7

---