STEREOMETRIA
Wzajemne położenie prostych w przestrzeni
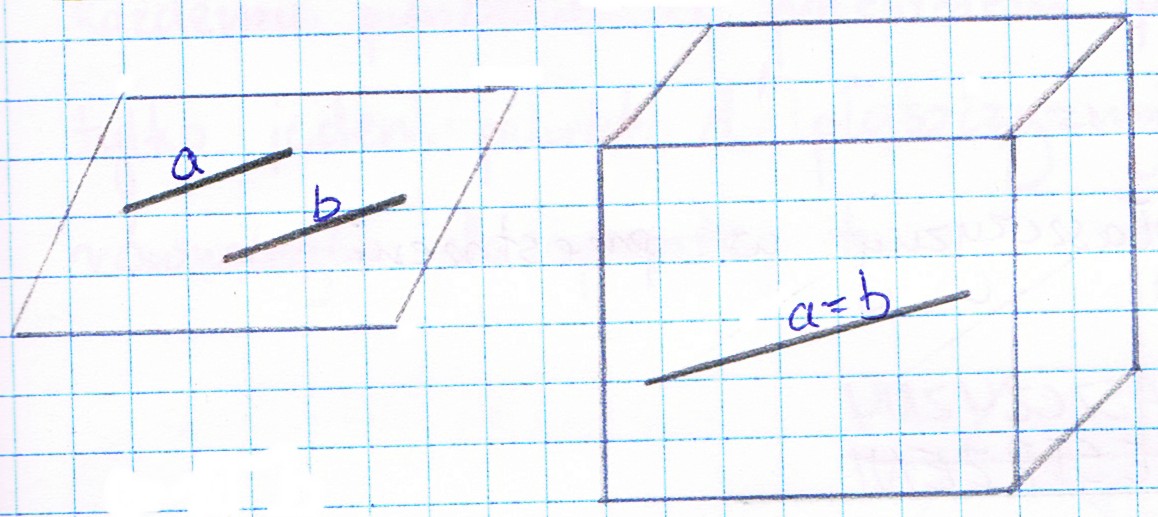
Proste równoległe w przestrzeni są to proste, które leżą w jednej płaszczyźnie i nie mają punktów wspólnych albo pokrywają się.
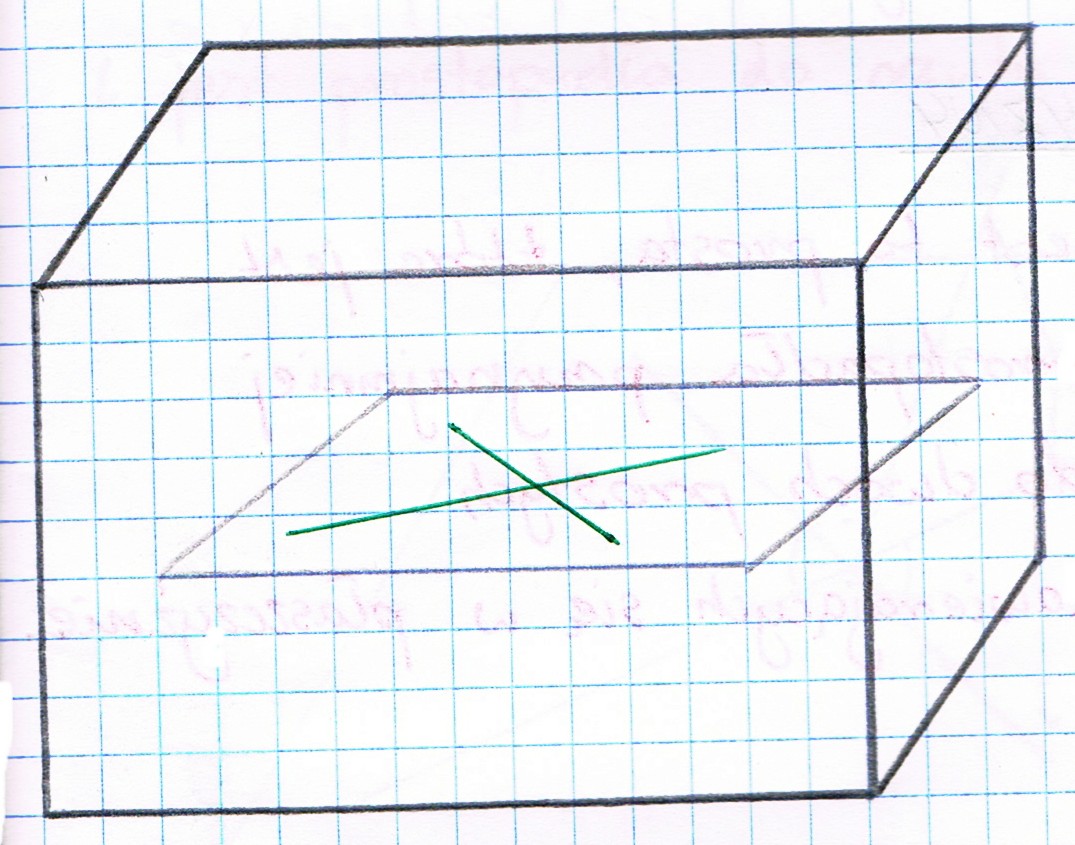
Proste skośne w przestrzeni są to proste, które nie leżą w jednej płaszczyźnie i nie mają punktów wspólnych.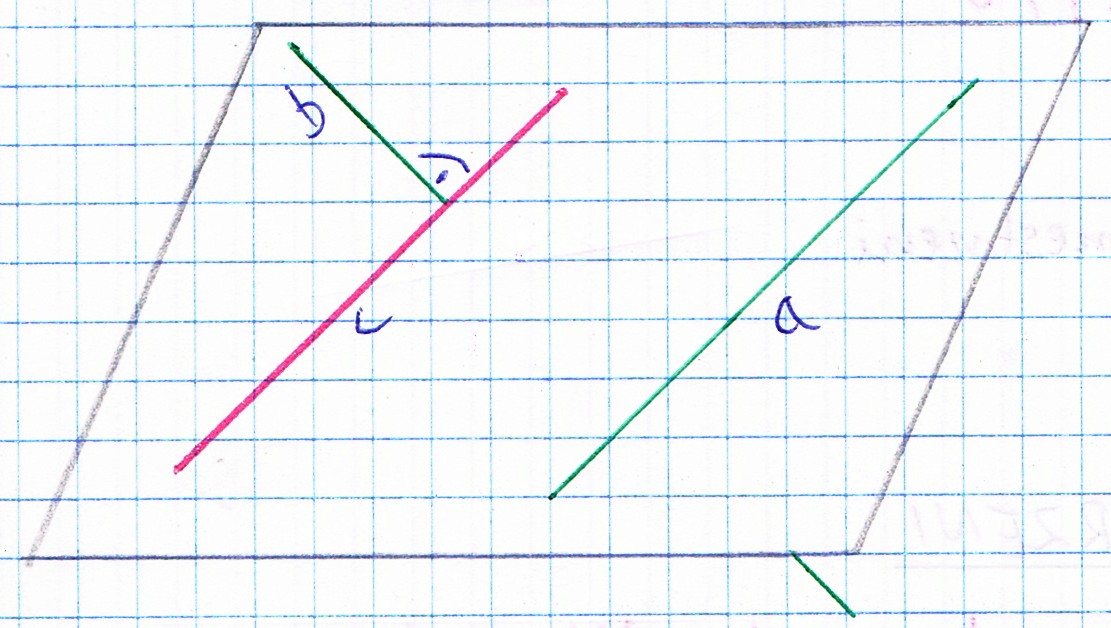
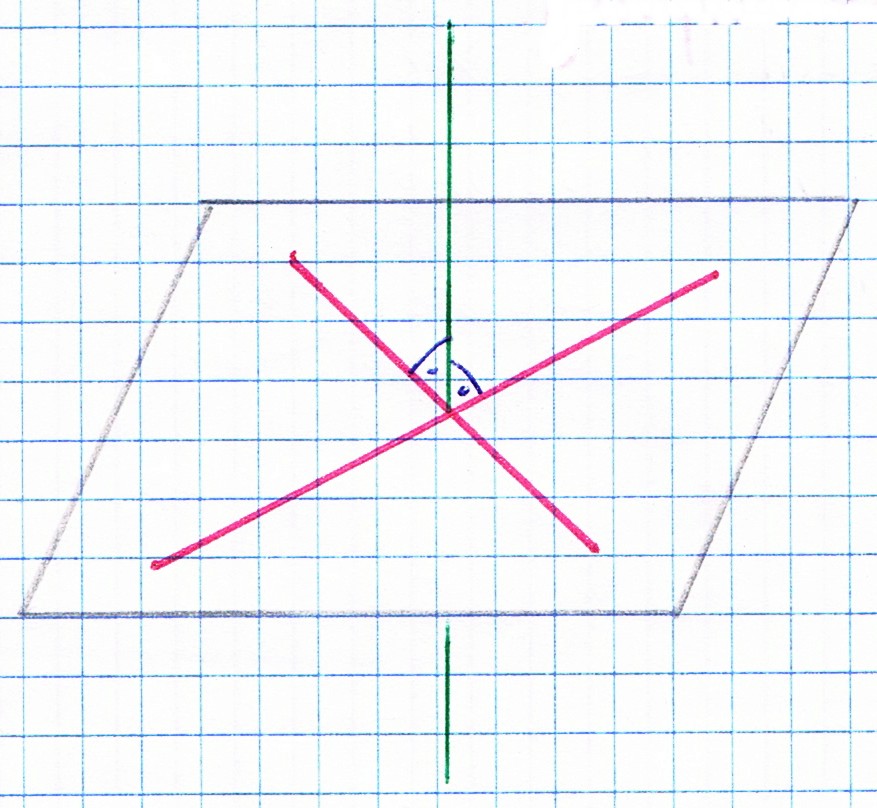
Proste przecinające się w przestrzeni są to proste, które leżą w jednej płaszczyźnie i mają punkt wspólny.Proste prostopadłe w przestrzeni są to proste, dla których istnieje prosta równoległa do jednej z nich przecinająca drugą pod kontem prostym.
.
![]()
Wzajemne położenie prostej i płaszczyzny w przestrzeni
Prosta równoległa do płaszczyzny jest to prosta, która nie ma punktów wspólnych z płaszczyzną albo zawiera się w płaszczyźnie.
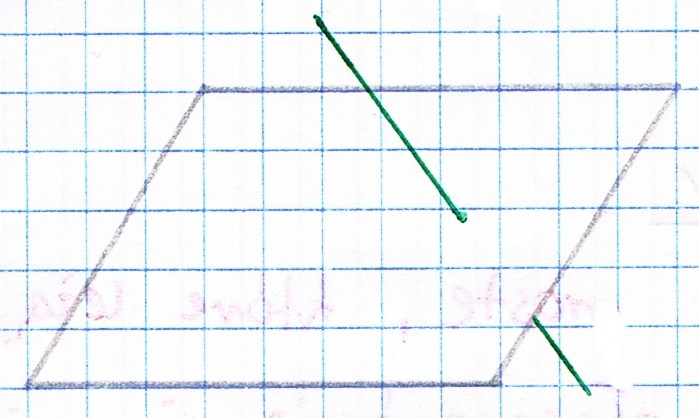
Prosta przecinająca płaszczyznę jest to prosta, która ma jeden punkt wspólny z płaszczyzną.Prosta prostopadła do płaszczyzny jest to prosta, która jest prostopadła przynajmniej do dwóch prostych zawierających się w płaszczyźnie.
Rzut prostokątny na płaszczyznę
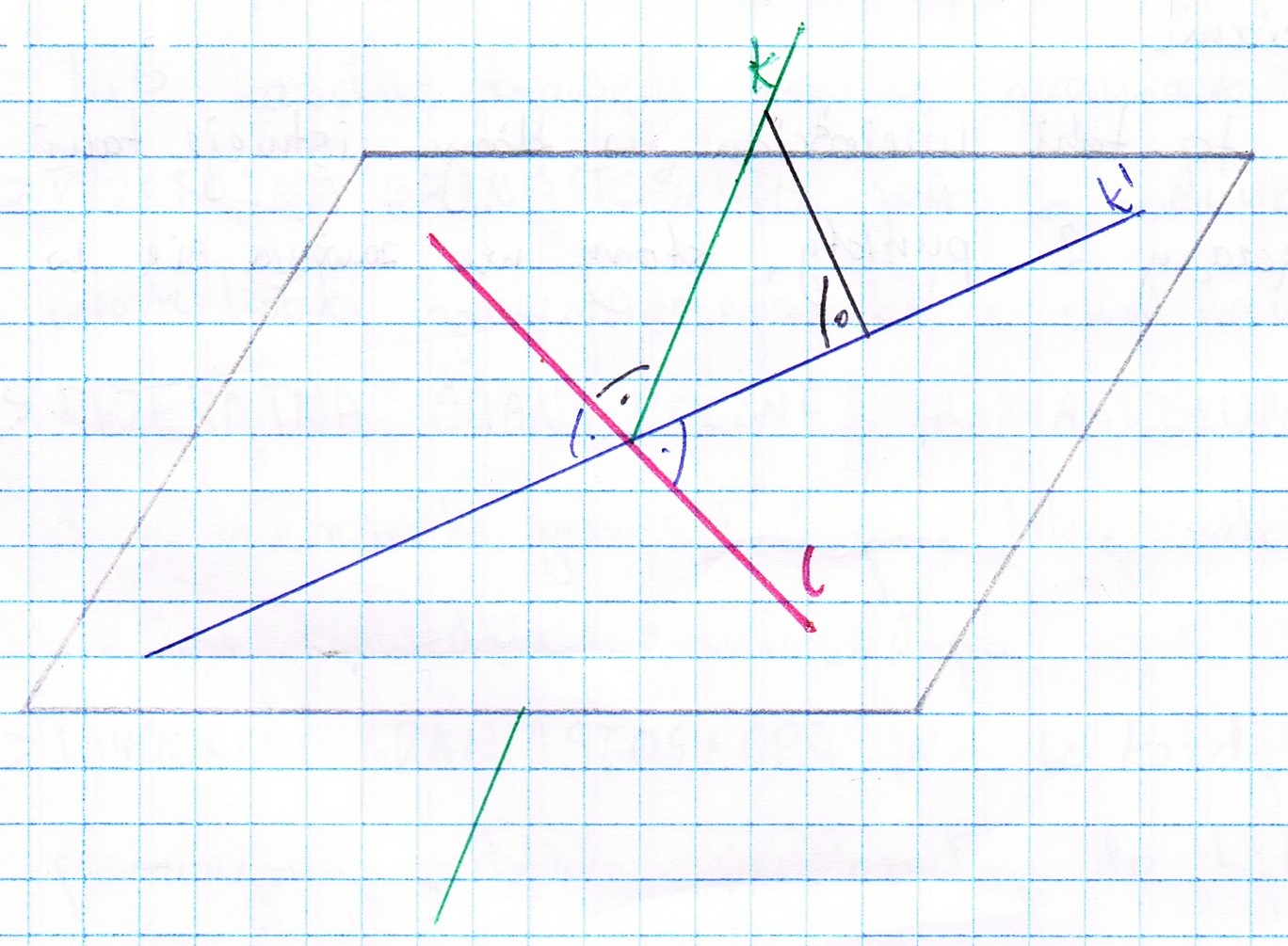
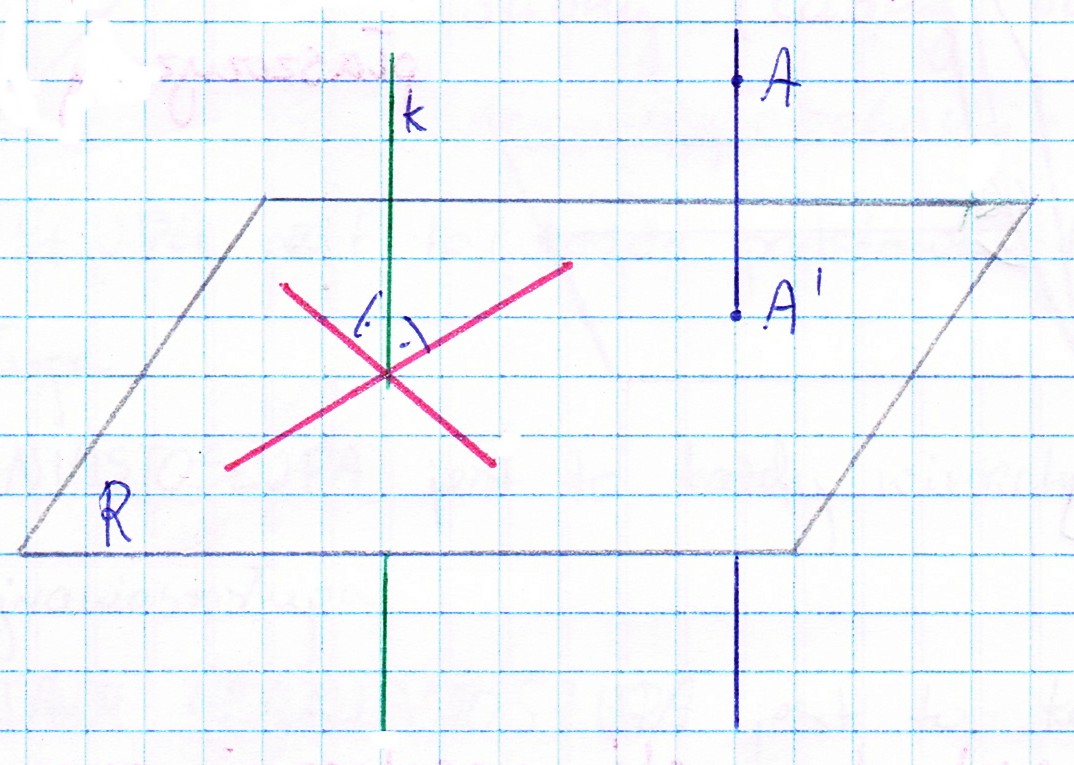
Rzut prostokątny punktu A przestrzeni na płaszczyznę R, w kierunku prostej k prostopadłej do płaszczyzny R jest to przekształcenie geometryczne, w którym każdemu punktowi A przestrzeni przyporządkowany jest jeden i tylko jeden punkt A' płaszczyzny R, taki że prosta AA' jest równoległa do prostej k.Twierdzenie o trzech prostych prostopadłych
Niech k będzie prostą, która nie jest równoległa ani prostopadła do płaszczyzny R, a l prostą zawierającą się w płaszczyźnie R i przechodzącą przez punkt wspólny prostej k i płaszczyzny R.
Prosta l jest prostopadła do prostej k, wtedy i tylko wtedy, gdy prosta l jest prostopadła do rzutu k' prostej k na płaszczyznę R.
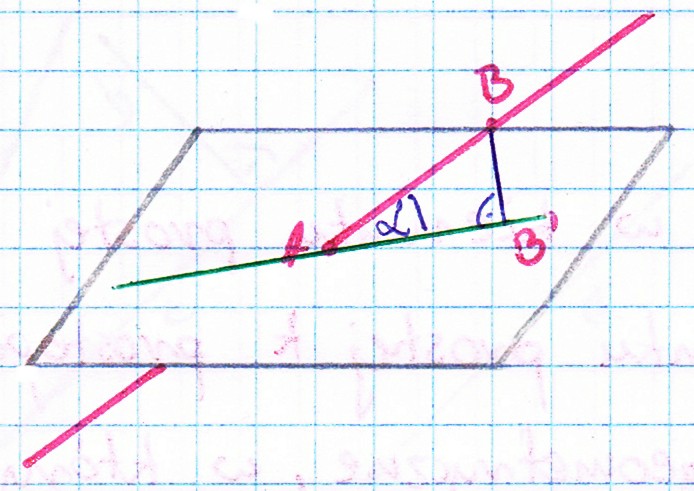
Kąty w przestrzeni
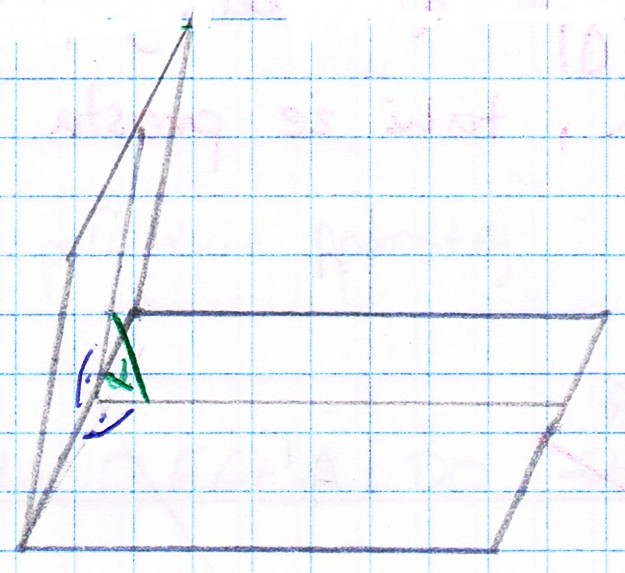
Kąt między prostą a płaszczyzną jest to kąt między daną prostą a jej rzutem prostokątnym na płaszczyznę.Kąt dwuścienny jest to każda z dwóch części przestrzeni, na którą dzielą przestrzeń dwie płaszczyzny o wspólnej krawędzi.
Wielościany
Wielościan jest to część przestrzeni ograniczona ze wszystkich stron wielokątami leżącymi w różnych płaszczyznach w taki sposób, że każda krawędź jest wspólna dla dwóch wierzchołków wraz z tymi wielokątami.
Wielościan wypukły to taki wielościan, w którym każdy z odcinków łączących dwa dowolne punkty zawiera się w wielościanie.
Wielościan wklęsły to taki wielościan, w którym istnieje taki odcinek łączący dwa punkty, który nie zawiera się w wielościanie.
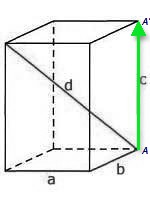
Graniastosłupy
Graniastosłup jest to wielościan, w którym można wskazać dwie ściany (podstawy) będące przystającymi wielokątami leżącymi w równoległych płaszczyznach, a pozostałe ściany (ściany boczne) są równoległobokami.
Ściana graniastosłupa jest to każda podstawa lub ściana boczna graniastosłupa.
Wierzchołek graniastosłupa jest to każdy wierzchołek wielokąta będącego podstawą graniastosłupa.
Krawędź podstawy graniastosłupa jest to każdy bok wielokąta będącego podstawą graniastosłupa.
Krawędź boczna graniastosłupa jest to każdy odcinek łączący te wierzchołki podstaw graniastosłupa, z których jeden jest obrazem drugiego w pewnym rzucie równoległym w kierunku wektora AA'.
Krawędź graniastosłupa jest to każda krawędź podstawy lub każda krawędź boczna graniastosłupa.
Przekątna graniastosłupa jest to odcinek łączący dwa wierzchołki graniastosłupa, który nie należy do żadnej jego ściany.
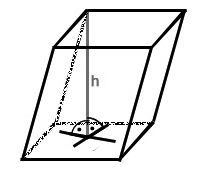
Przekątna ściany bocznej graniastosłupa jest to odcinek łączący dwa wierzchołki graniastosłupa, który należy do jego ściany i nie jest krawędzią graniastosłupa.Wysokość graniastosłupa jest to każdy odcinek łączący płaszczyzny podstaw i prostopadły do tych płaszczyzn.
Graniastosłup prosty jest to graniastosłup, w którym krawędzie boczne są prostopadłe do podstaw.
Graniastosłup pochyły (ukośny) jest to graniastosłup, w którym krawędzie boczne nie są prostopadłe do podstaw.
Graniastosłup prawidłowy jest to graniastosłup prosty, w którym podstawy są wielokątami foremnymi.
Graniastosłup wypukły jest to graniastosłup, w którym podstawy są wielokątami wypukłymi.
Graniastosłup wklęsły jest to graniastosłup, w którym podstawy nie są wielokątami wypukłymi.
Równoległościan jest to graniastosłup, w którym wszystkie ściany są równoległobokami.
Prostopadłościan jest to równoległościan, w którym wszystkie ściany są prostokątami.
Sześcian jest to prostopadłościan, w którym wszystkie ściany są kwadratami.
Ostrosłupy
Ostrosłup jest to wielościan, w którym można wskazać ścianę (podstawę) będącą dowolnym wielokątem, a pozostałe ściany (ściany boczne) są trójkątami o wspólnym wierzchołku.
Ściana ostrosłupa jest to podstawa lub każda ściana boczna ostrosłupa.
Wierzchołek ostrosłupa jest to część wspólna wszystkich ścian bocznych ostrosłupa.
Wierzchołek podstawy ostrosłupa jest to każdy z wierzchołków wielokąta będącego podstawą ostrosłupa.
Wierzchołek w ostrosłupie jest to wierzchołek ostrosłupa lub wierzchołek podstawy ostrosłupa.
Krawędź podstawy ostrosłupa jest to każdy bok wielokąta będącego podstawą ostrosłupa.
Krawędź boczna ostrosłupa jest to każdy odcinek łączący wierzchołki podstawy ostrosłupa z wierzchołkiem ostrosłupa.
Krawędź ostrosłupa jest to każda krawędź podstawy lub każda krawędź boczna ostrosłupa.
Wysokość ostrosłupa jest to odcinek łączący wierzchołek ostrosłupa z płaszczyzną podstawy i prostopadły do tej płaszczyzny. (analogicznie do wysokości graniastosłupa)
Spodek wysokości ostrosłupa jest to koniec wysokości leżący na płaszczyźnie podstawy.
Ostrosłup prosty jest to ostrosłup, którego spodek wysokości jest środkiem okręgu opisanego na podstawie.
Ostrosłup pochyły (ukośny) jest to ostrosłup, którego spodek wysokości nie jest środkiem okręgu opisanego na podstawie.
Ostrosłup prawidłowy jest to ostrosłup prosty, w którym podstawa jest wielokątem foremnym.
Ostrosłup wypukły jest to ostrosłup, w którym podstawa jest wielokątem wypukłym.
Ostrosłup wklęsły jest to ostrosłup, w którym podstawa nie jest wielokątem wypukłym.
Czworościan jest to ostrosłup trójkątny.
Czworościan foremny jest to czworościan, którego wszystkie ściany są trójkątami równobocznymi.
Gdy rysujemy wielościany, musimy przestrzegać następujących reguł:
Jeśli w wielościanie odcinki są równoległe, to odpowiadające im odcinki na rysunku także są równoległe.
Jeśli w wielościanie odcinki są równoległe i równej długości, to odpowiadające im odcinki na rysunku też są równoległe i równej długości.
Jeśli punkt dzieli odcinek w wielościanie w pewnym stosunku, to odpowiadający mu punkt na rysunku dzieli odcinek w tym samym stosunku.
WZÓR EULERA
S+W=K+2
S - ściany
W - wierzchołki
K - krawędzie
Funkcjonuje on dla dowolnego wielościanu wypukłego.
n |
Wierzchołki |
Krawędzie |
Ściany |
|
n |
Wierzchołki |
Krawędzie |
Ściany |
3 |
6 |
9 |
5 |
|
3 |
4 |
6 |
4 |
4 |
8 |
12 |
6 |
|
4 |
5 |
8 |
5 |
5 |
10 |
15 |
7 |
|
5 |
6 |
10 |
6 |
n |
2n |
3n |
n+2 |
|
n |
n+1 |
2n |
n+1 |
n - liczba wierzchołków w podstawie
Wyszukiwarka
Podobne podstrony:
stereotypy 5
Stereotypy 3
Prezentacja stereopsja 2
11 Stereochemia i podstawowa nomenklatura sacharydów i polisacharydów
91 Nw 05 Amator stereo
Przedwzmacniacz Stereo z Regulacją Tonów, pcb 3xna stronie
powt przed maturą, StereometriaN
Stereometria Łatwa
stereometria, Szkoła-LO, MATEMATYKA
Pomiar widzenia stereoskopowego, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr III, ergonomia
stereotyp psych
69 Rola stereotypów i uprzedzeń w komunikowaniu międzynarodowym
MTC CR3000 Car Stereo Head Unit
Farina Reproduction of auditorium spatial impression with binaural and stereophonic sound systems
Penncrest 5905 Stereo Receiver
3 Mechanizm Stereotypizacji
stereotyp kobiecości, studia pedagogiczne, Psychologia rozwoju człowieka
stereotypy, Interesujące, SOCJOLOGIA (materiały)
więcej podobnych podstron