Marek Wolny

Politechnika Wrocławska

Ocena:

Wydział Budownictwa Lądowego i Wodnego

Numer albumu: 162263

Ćwiczenie 57c.

Badanie efektu Halla.

Wstęp.

1. Wykres zależności napięcia Halla od kąta odczytanego z podziałki hallotronu.

2. Zadaniem jest odczytanie wartości kąta
   dla której
   zatem
   .

3. Kolejnym zadaniem jest obliczenie maksymalnej wartości czułości kątowej hallotronu

obliczając nachylenie wykresu
dla wartości
z przedziału
od
(tj. dla wartości
od -0,1653 do 0,1653). Obliczam to korzystając z programu Reg.zip zamieszczonego na stronie internetowej Laboratorium Podstaw Fizyki.

Po podstawieniu liczb do programu dostajemy wynik
Niepewność wyznaczeniu
zatem
=0,006428.

4. Wykres zależności napięcia Halla
   od wartości składowej normalnej

indukcji

5. Korzystając z regresji liniowej obliczyłem wartości współczynników kierunkowych prostej opisujących zależności
   gdy
   

Stąd:

6. Czułość γ hallotronu obliczamy ze wzoru:

65,1

7. Niepewność wyznaczenia czułości hallotronu otrzymujemy ze wzoru:

=0,02

8. Obliczamy koncentrację elektronów swobodnych korzystając ze wzoru:

Gdzie:

D - grubość płytki hallotronu (
)

E - ładunek elementarny (
)

9. Niepewność obliczenia koncentracji elektronów obliczamy ze wzoru:

Gdzie:

0,05

10. Obliczenia wartości znajdujących się w tabeli.

Błąd wyznaczenia natężenia:

A

Wartość składowej normalnej indukcji wyznaczyłem ze wzoru:

Gdzie:

0,500 T

Błąd względny wyznaczenia czułości hallotronu:

Błąd względny obliczenia koncentracji elektronów swobodnych:

Błąd
przyjmuję najmniejszym możliwą jednostką jaką możemy odczytać ze skali, która wynosi 1°.

	∆	B	∆B		∆	α	∆α	γ	∆γ		n	∆n
						[°]	[°]			%			%
11	0,075	-0,499	0,05	-0,3752	0,0001	10	1	65,11	1,272	0,02		4,03
		-0,495		-0,3746	0,0001	0
		-0,475		-0,3651	0,0001	350
		-0,489		-0,3648	0,0001	20
		-0,440		-0,358	0,0001	340
		-0,463		-0,3454	0,0001	30
		-0,393		-0,3208	0,0001	330
		-0,423		-0,3147	0,0001	40
		-0,333		-0,2846	0,0002	320
		-0,371		-0,2753	0,0002	50
		-0,264		-0,2385	0,0002	310
		-0,307		-0,2263	0,0002	60
		-0,186		-0,1911	0,0002	300
		-0,234		-0,1758	0,0002	70
		-0,103		-0,1302	0,0002	290
		-0,154		-0,1175	0,0002	80
		-0,016		-0,0674	0,0003	280
		-0,069		-0,0535	0,0003	90
		0,07		-0,0021	0,0003	270
		0,017		0,0127	0,0003	100
		0,155		0,0649	0,0003	260
		0,103		0,0766	0,0003	110
		0,235		0,1237	0,0004	250
		0,187		0,1347	0,0004	120
		0,308		0,1812	0,0004	240
		0,264		0,1903	0,0004	130
		0,371		0,2287	0,0004	230
		0,334		0,2374	0,0004	140
		0,424		0,2689	0,0004	220
		0,393		0,2752	0,0004	150
		0,463		0,2965	0,0004	210
		0,441		0,3054	0,0005	160
		0,489		0,3188	0,0005	200
		0,475		0,3215	0,0005	170
		0,499		0,3304	0,0005	190
		0,495		0,3305	0,0005	180

Wersja Dodatkowa.

1. Wykres przedstawiający zależność napięcia Halla
   od natężenia prądu
   płynącego przez hallotron.

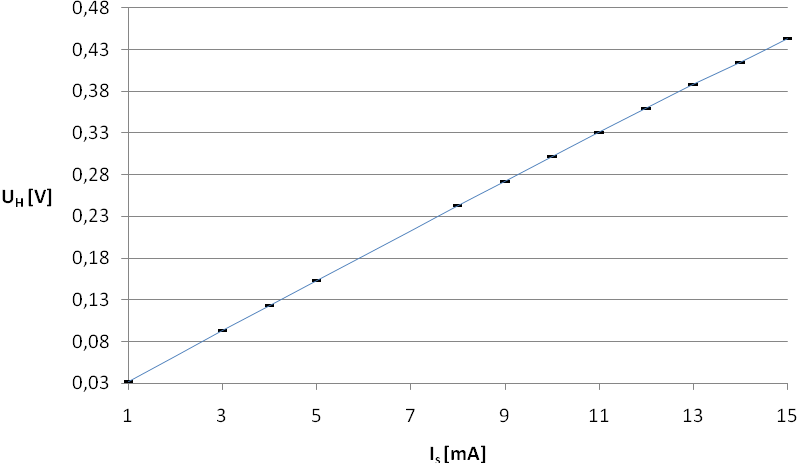
2. Używając regresji liniowej obliczam współczynniki kierunkowe prostych

opisujących zależności
gdy

Stąd:

3. Obliczam czułość hallotronu korzystając z wcześniejszych obliczeń:

4. Niepewność obliczenia czułości hallotronu obliczamy metodą pochodnej logarytmicznej:

5. Obliczamy koncentrację elektronów swobodnych korzystając ze wzoru:

Gdzie:

D - grubość płytki hallotronu (
)

E - ładunek elementarny (
)

6. Niepewności: względną i bezwzględną obliczamy ze wzorów:

B	∆B		∆		∆	α	∆α	γ	∆γ		n	∆n
						[°]	[°]			%			%
0,495	0,05	1	0,075	0,0317	0,0003	180	1	58,58	6,1	10,41			15,41
		2		0,0623	0,0003
		3		0,0932	0,0003
		4		0,1229	0,0004
		5		0,1529	0,0004
		6		0,1826	0,0004
		7		0,2124	0,0004
		8		0,2427	0,0004
		9		0,2719	0,0004
		10		0,3015	0,0005
		11		0,3309	0,0005
		12		0,3596	0,0005
		13		0,3882	0,0005
		14		0,4145	0,0005
		15		0,4428	0,0005

Analiza niepewności.

Na niepewność naszych pomiarów miał wpływ m.in. małodokładny kątomierz, którym wyznaczaliśmy kąt nachylenia magnesu. Trzeba było założyć, że odczyt z podziałki kątomierza położenia magnesu, dla którego wektor indukcji magnetycznej jest równoległy do wektora prędkości elektronów jest obarczony jest błędem 1°. Przez powyższy błąd nie byliśmy w stanie części składowej wektora indukcji, który jest wywiera wpływ na ruch elektronów w płytce. W konsekwencji wykres pomiarów nie pokrywa się w połowie z wykresem wyznaczonym za pomocą regresji liniowej.

Z pewnością na niepewność doświadczenia miał wpływ fakt, iż używaliśmy magnesu sztabkowego o indukcji 0,5T a nie mocniejszego elektromagnesu. Wpływ na wyniki miał również fakt, że indukcja była wyznaczana z błędem 0,05 tj. 10% w stosunku do obliczonej wartości.

Niewielki udział w niedokładności doświadczenia miały przyrządy do pomiaru natężenia i napięcia. W porównaniu z wyżej wymienionymi niepewnościami były one jednak niewielkie.

Wnioski.

Celem ćwiczenia było zapoznanie się z efektem Halla oraz wyznaczenie koncentracji elektronów swobodnych. Wyznaczona przez nas koncentracja elektronów jest obarczona błędem względnym 6,9% dla pomiarów zależności napięcia Halla
od indukcji magnetycznej B gdy
oraz 15,41% dla pomiarów zależności napięcia
od natężenia
przy stałej indukcji magnetycznej B.

Dokładność naszego doświadczenia możemy zwiększyć stosując precyzyjniejszy kątomierz. Dokładność zwiększyłaby się również gdybyśmy zastosowali magnes o większej indukcji.

---