Fal Jacek 04.04.2006

Sprawozdanie z ćwiczenia nr 20.

Wyznaczanie energii aktywacji przewodnictwa materiałów półprzewodnikowych.

1. Zagadnienia do samodzielnego opracowania.

W ciele stałym atomy zbliżają się na odległości porównywalne z rozmiara­mi samych atomów. Każdy elektron znajduje się pod wpływem wszystkich in­nych, bliskich jonów. Każdy poziom energetyczny atomu może rozszczepiać się na bardzo liczne, bliskie poziomy energetyczne. Poziomy wewnętrzne rozszcze­piają się nieznacznie na skutek wpływu jąder, poziomy zaś zewnętrzne znacznie, tworząc tzw. pasma. W pasmach tych mogą przebywać elektrony przedzielone pasmami wzbronionymi. W najwyższym paśmie elektrony są bardzo słabo związane z jądrem, można je uważać za swobodne. W obszarze jednego pasma elektrony mogą łatwo przechodzić z jednego poziomu energetycznego na drugi, gdyż różnice są niewielkie, lecz nie może być przekroczony zakaz Pauliego-Jeżeli w paśmie wszystkie stany energetyczne są obsadzone zgodnie z zasadą Pauliego, to ruchu elektronów nie będzie. O takim paśmie mówimy, że jest pa­smem zapełnionym (walencyjnym). Jeżeli dane pasmo jest tylko częściowo za­pełnione, to są możliwe przejścia na poziomy energetyczne wyższe i takie p^a' smo nosi nazwę pasma przewodnictwa. Aby kryształ przewodził prąd, w paśmtf przewodnictwa muszą znajdować się elektrony i również nie zajęte poziomy, gdyż ruch elektronów w polu elektrycznym jest związany z powiększeniem '^c energii kinetycznej, a więc z przenoszeniem się na wyższe poziomy. Tak zwyk jest w metalach i dzięki temu są one przewodnikami. Jeżeli pasma walencyjne ^S4 całkowicie zapełnione, a wyższe całkowicie puste i przerwa energetyczna duża to kryształ jest izolatorem. Następną grupę stanowią półprzewodniki, w których pasmo przewodnictwa jest puste, lecz pasmo energii wzbronionej jest wąskie i często energia cieplna wystarcza, aby pewną liczbę elektronów przerzucić do pasma przewodnictwa. Toteż kryształy tego typu przewodzą prąd zwykle słabo, przewodnictwo tych substancji rośnie w wysokiej temperaturze.

Z punktu widzenia klasycznej teorii elektronowej dużą przewodność metali tłumaczy się występowaniem w nich dużej liczby nośników prądu - elektronów przewodzenia wędrujących po całej objętości przewodnika. Drude założył, że elektrony przewodzenia w metalu można rozpatrywać jako „gaz elektronowy", wykazujący cechy jednoatomowego gazu idealnego. Podczas ruchu elektrony przewodzenia zderzają się z jonami siatki krystalicznej metalu. Można zatem mówić o średniej długości drogi X elektronów, która pod względem wielkości powinna być równa stałej siatki krystalicznej metalu (1(T⁸ cm). Na podstawie praw teorii kinetycznej gazów określimy średnią energię kinetyczną ruchu cieplnego elektronów:

gdzie: m - masa elektronu,

u - średnia prędkość elektronów (w temperaturze 0°C - u = 110 km/s).

Ruch cieplny elektronów wskutek swojej chaotyczności nie może spowo­dować przepływu prądu elektrycznego. Jeżeli natomiast do przewodnika przyło­żymy zewnętrzne pole elektryczne, to wzdłuż przewodnika odbywa się ruch elektronów od potencjału wyższego do niższego, aż do chwili ich wyrównania. Pod wpływem pola elektrycznego na bezładny (cieplny) ruch elektronów nakła­da się ruch uporządkowany w kierunku przeciwnym do kierunku wektora E-Uporządkowany ruch ładunków, ściślej, ruch cząstek naładowanych nazywamy prądem elektrycznym, przy czym ruch cząstek naładowanych dodatnio przyj­mujemy za równoważny z prądem wywołanym ruchem cząstek naładowanych ujemnie, lecz poruszających się w kierunku przeciwnym. Za kierunek prądu przyjęto umownie kierunek poruszania się ładunków dodatnich. Za przepłyń prądu w metalach są odpowiedzialne elektrony, w elektrolitach - jony dodatnie i ujemne, w gazach - elektrony oraz jony dodatnie i ujemne.

Wielkością charakteryzującą w sposób ilościowy przepływ prądu jest natę­żenie prądu /. Natężeniem prąciu I nazywamy stosunek ładunku elektrycznego dQ> przepływaj ącego przez dany przekrój przewodnika, do czasu dt przepływu _tego ładunku:

Jednostką natężenia prądu jest amper [A]. Przy natężeniu 1 A przez dany przekrój przepływa w ciągu 1 s ładunek wartości 1C.

Prąd, którego natężenie nie zmienia się w czasie, nazywamy prądem stałym (stacjonarnym). W przypadku prądu stałego natężenie prądu jest równomiernie rozłożone w całym przekroju przewodnika. Warunek ten nie jest spełniony w przypadku prądów szybko zmieniających się w czasie. Do opisania tych prą­dów wprowadza się, oprócz pojęcia natężenia prądu, termin gęstości natężenia prądu.

Gęstość natężenia prądu jest wektorem, którego kierunek i zwrot są zgodne z kierunkiem ruchu ładunków dodatnich dQ, przepływających w czasie dt, pro­stopadle do powierzchni przekroju, przez element dS tej powierzchni. Jego wartość liczbowa wynosi:

lub

Jeżeli prąd elektryczny jest wywołany ruchem ładunków dodatnich i ujem­nych, to gęstość natężenia prądu

gdzie: j₊ - gęstość prądu wywołanego ruchem ładunków dodatnich, j_ - gęstość prądu wywołanego ruchem ładunków ujemnych.

Rozważmy ogólny przypadek, czyli ruch ładunków w trójwymiarowej Przestrzeni. Wówczas wygodnie jest posługiwać się gęstością natężenia prądu.

W jednostce objętości niech znajduje się średnio n cząstek i ładunek każdej ² nich niech będzie równy e. Przyjmijmy, że ładunki te poruszają się ze średnią Prędkością v_śr

2. Wykonanie ćwiczenia.

Układ pomiarowy składa się z łaźni wodnej, w której jest zamocowany ba­dany element z możliwością pomiaru jego temperatury.

1. Napełnić łaźnię wodną wodą do określonego poziomu.

2. Połączyć układ pomiarowy według schematu pokazanego na rys.

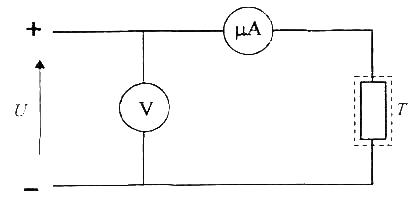
3. Po sprawdzeniu obwodu elektrycznego przez prowadzącego ćwiczenia oraz podaniu przez niego wartości napięcia zasilającego włączyć obwód i od­ czytać wartości natężenia prądu płynącego w obwodzie. Jednocześnie odczytać z termometru temperaturę, w jakiej dokonano pomiaru.

4. Włączyć piecyk łaźni wodnej T i w trakcie ogrzewania odczytywać wartości natężenia prądu płynącego w obwodzie dla wybranych wartości tempe­ratury (od temperatury pokojowej do temperatury 85°C co 5°C).

5. Na papierze milimetrowym nanieść punkty pomiarowe zależności:

. Punkty te będą się układać na prostych o współczynnikach nachy­lenia a₁ i a₂.

6. Wyznaczyć wartość energii aktywacji dla obszaru przewodnictwa samoistnego i niesamoistnego (ε₁ i ε₂).

3. Tabela pomiarowa.

Lp.	U [ ]	T [ ]	[ ]	I [ ]	lnI	ε1 [ ]	ε2 [ ]




---