AKADEMIA TECHNICZNO-ROLNICZA W BYDGOSZCZY INSTYTUT MATEMATYKI I FIZYKI

LABORATORIUM Z FIZYKI

Ćwiczenie nr 2 Temat: Pomiar przyśpieszenia ziemskiego

Imię i nazwisko: Michał Rudziński Semestr II Grupa B Data: 30.02.2003

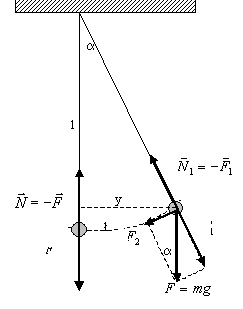
Wahadłem matematycznym płaskim nazywamy punkt materialny poruszający się po łuku w polu grawitacyjnym.

Zależność okresu drgań T wahadła matematycznego od maksymalnego kąta wychylenia ϕ_m:

Ze wzoru wynika, że okres drgań wahadła rośnie wraz ze wzrostem maksymalnego wychylenia. Można przyjąć (dla kątów ϕ<π/2), że powyższy wzór ma następującą postać:

Gdy będziemy zmniejszać wartość kąta, to w końcu przy ϕ→0 okres przestanie zależeć od wychylenia i otrzymamy:

Występują wówczas drgania harmoniczne (siła proporcjonalna do wychylenia). W praktyce, z powodu niedokładności przyrządów pomiarowych przedział wartości ϕ, w którym okres T jest niezależny od wychylenia jest szerszy.

Przyspieszenie ziemskie wygodniej wyliczyć przy pomocy wahadła różnicowego, w celu zminimalizowania błędów pomiaru długości. Używając wahadła matematycznego, przeprowadza się kilka eksperymentów dla różnej długości (a tego samego kąta maksymalnego wychylenia), a następnie przeprowadza wyliczenia dla różnicy długości, którą można zmierzyć o wiele precyzyjniej.

Tak więc dla długości l0 okres drgań będzie:

zaś dla innej mniejszej długości l_i będzie krótszy i wyniesie:

Podnosząc oba równania do kwadratu i odejmując stronami po przekształceniach otrzymamy:

W naszych pomiarach kąt wychylenia był bardzo mały wiec wzór wyglądał tak:

ĆWICZENIE 2A

Tabele pomiarowe

Przyspieszenie ziemskie wynosi:

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla l₁ i l₂:

Niepewność całkowita dla T₁:

Niepewność całkowita dla T₂:

Wartości pochodnych cząstkowych :

Podstawiając wszystkie wartości otrzymujemy:

Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wynik pomiaru:

CWICZENIE 2B

Tabele pomiarowe

Przyspieszenie ziemskie wynosi:

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla d:

Niepewność całkowita dla T:

Wartości pochodnych cząstkowych :

Podstawiając wszystkie wartości otrzymujemy:

Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wynik pomiaru:

ĆWICZENIE 2C

WAHADŁO MATEMATYCZNE

Tabela pomiarowa

Obliczenia:

Przyspieszenia ziemskie wynosi:

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla l:

Niepewność całkowita dla T:

Wartości pochodnych cząstkowych :

Podstawiając wszystkie wartości otrzymujemy:

Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wynik pomiaru:

WAHADŁO REWERSYJNE

Tabela pomiarowa

Obliczenia:

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla d:

Niepewność całkowita dla T:

Wartości pochodnych cząstkowych :

Podstawiając wszystkie wartości otrzymujemy:

Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wynik pomiaru:

Wnioski:

Jedna z przyczyn niedokładności pomiaru jest kąt z jakim były wychylane wszystkie te wahadła. Na pewno był on inny dla każdego pomiaru ponieważ wychylenie wahadła było wykonywane przez studenta bez użycia żadnych urządzeń pomiarowych.

Trzeba również zauważyć że przyspieszenie ziemskie nie jest jednakowe w każdym punkcie na Ziemi, dlatego wyniki pomiaru są różne od książkowych danych.

Ponadto puszczając krążek ( lub kulkę ) , nie zawsze udawało się nadać mu ruch w jednej płaszczyźnie, dlatego by zminimalizować błąd, odczytywaliśmy dopiero 3 pomiar zegara. Niestabilność statywu i rozciąganie się nici tez ma wpływ na niedokładność pomiaru.

---