Przestrzenna transformacja współrzędnych

1. Wstęp

Transformacja współrzędnych pomiędzy dwoma układami geodezyjnymi, zwanymi pierwotnym i wtórnym, polega na przekształceniu współrzędnych z układu pierwotnego do układu wtórnego na podstawie punktów posiadających współrzędne w obu układach zwanych punktami łącznymi.

Na podstawie współrzędnych punktów łącznych tworzone są algorytmy transformacji.

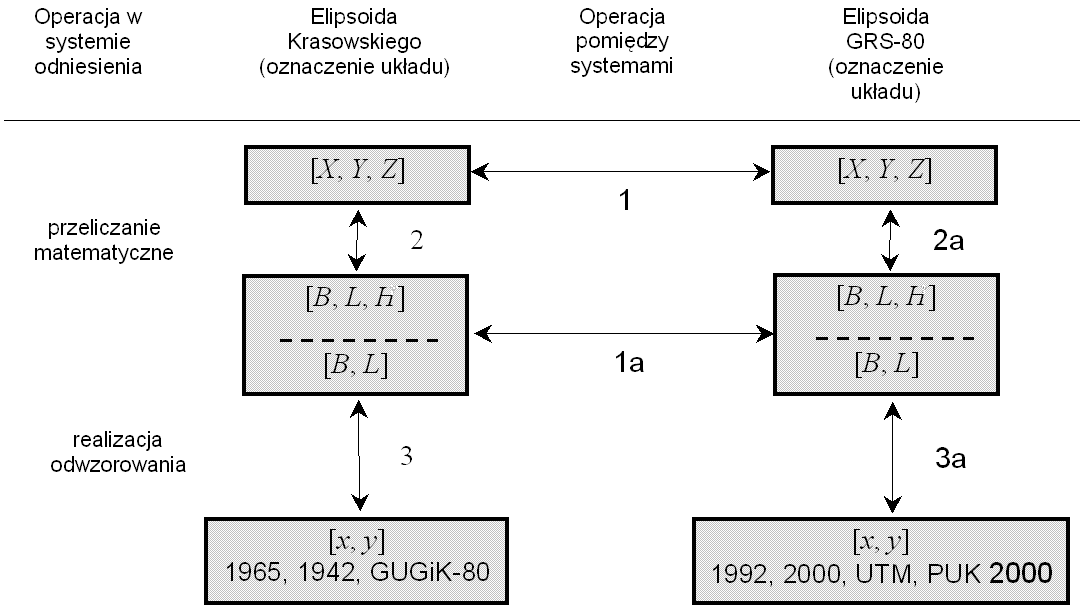
Każda operacja przejścia z jednego układu do drugiego odbywa się za pośrednictwem ściśle określonych funkcji transformacyjnych (odwzorowawczych) i ich parametrów liczbowych.

Elipsoidy Krasowskiego i GRS-80 nie są ściśle koncentryczne a ich osie nie są równoległe. Pomiędzy układami obu elipsoid zachodzą związki transformacji przestrzennej przyjmowanej jako transformacja przez podobieństwo (7 - parametrowa).

Na parametry tej transformacji składają się:

1. trzy przesunięcia,

2. trzy obroty osiowe,

3. zmiana skali.

Powyższe parametry wyznaczono (estymowano) w Głównym Urzędzie Geodezji i Kartografii na podstawie punktów sieci POLREF. Aby takie wyznaczenie mogło mieć miejsce, punkty te musiały posiadać współrzędne wyznaczone w obu układach elipsoidalnych.

2. Transformacja: [X₁,Y₁,Z₁] => [X₂,Y₂,Z₂]

Transformacja Helmerta pozwala na przejście (transformację) z jednego układu kartezjańskiego do układu drugiego, także kartezjańskiego. Ogólna postać tej transformacji jest określona poniższym wzorem:

gdzie:

X₂ - układ wtórny,

c - wektor translacji układu,

R - macierz rotacji.

X₁ - układ pierwotny,

μ - poprawka do skali,

Wektor c translacji układu ma postać:

Macierz rotacji jest macierzą ortogonalną, składającą się z macierzy obrotów wokół osi głównych układu. Jej postać ogólna wygląda następująco:

Natomiast jej postać szczegółowa przedstawiona jest poniżej:

3. Transformacja: [B,L,h] => [X,Y,Z]

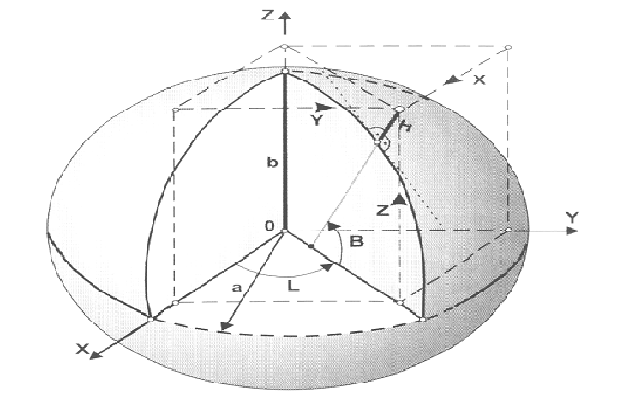
Pozycja dowolnego punktu na powierzchni Ziemi jest określana w sposób jednoznaczny na przykład za pomocą współrzędnych geodezyjnych (B, L, h) lub kartezjańskich geocentrycznych (X, Y, Z) w umownym systemie elipsoidalnym. Te dwa rodzaje współrzędnych traktowane są jako informacje równoważne, ponieważ przejście (przeliczenie) pomiędzy nimi (z układu geodezyjnego do układu kartezjańskiego) dokonuje się poprzez ścisłe, wzajemnie jednoznaczne formuły matematyczne.

W układ elipsoidalny można wpisać układ kartezjański.

Przeliczenie współrzędnych elipsoidalnych na kartezjańskie można dokonać realizując wzory:

gdzie:

(*)

4. Transformacja: [X,Y,Z] => [B,L,h]

Aby dokonać przeliczenia odwrotnego, należy przekształcić powyższe wzory wyznaczając z nich B, L i h na podstawie X, Y, Z. Jednakże w definicji promienia N i wielkości q zawarta jest szerokość geodezyjna B. Jednym ze sposobów obliczenia szerokości geodezyjnej B jest metoda kolejnych przybliżeń. Zapiszemy:

(**)

Wzór powyższy nie oznacza jeszcze jawnego rozwiązania niewiadomej, jaką tu stanowi szerokość geodezyjna B. Jednakże wzór ten można przyjąć do tworzenia kolejnych przybliżeń niewiadomej B według następującego algorytmu:

Krok 1: przyjmuje się q = q₀ = 0 i obliczamy B₀ według wzoru (**), traktując wynik jako przybliżenie początkowe,

Krok 2: oblicza się przybliżoną wartość q₁ ze wzoru (*) jako funkcję B₀, a następnie nowe przybliżenie B₁ szerokości B według wzoru (**),

Krok 3: oblicza się przybliżenie q₂, zgodnie ze wzorem (*) jako funkcję B = B₁, a następnie aktualne przybliżenie B₂ szerokości B ze wzoru (**).

Procedurę kończy się, jeśli różnica kolejnych przybliżeń jest mniejsza niż założony dopuszczalny błąd numeryczny wyznaczenia szerokości geodezyjnej B.

Obliczenie pozostałych współrzędnych (rysunek) opiera się o realizację poniższych wzorów:

uwaga: jeżeli Δz < 0 lub Δr < 0, to prawą stronę równania mnożymy przez -1.

gdzie:

5. Transformacja: [X, Y, Z]_K => [X, Y, Z]_G

Pozycja wyznaczona za pomocą odbiornika GPS jest związana z elipsoidą GRS-80 (WGS-84). Dlatego też problem transformacji współrzędnych wywodzących się z różnych elipsoid jest bardzo istotny.

Parametry niezbędne do przeprowadzenia transformacji punktów o współrzędnych [X, Y, Z]_K w centrycznym układzie kartezjańskim elipsoidy Krasowskiego do współrzędnych [X, Y, Z]_G opartych o elipsoidę GRS-80 wyznaczono w Głównym Urzędzie Geodezji i Kartografii. Najbardziej ogólna formuła liniowej transformacji przestrzennej wyraża się następującymi wzorami:

lub w postaci macierzowej:

gdzie:

T - wektor przesunięcia środków układów,

D - macierz parametrów rotacji,

d_ij - elementy macierzy parametrów (i, j = 1, 2, 3).

Zgodnie z instrukcją techniczną G-1.10 elementy macierzy parametrów D mają następujące wartości:

d₁₁= 1- 0,84078048·10^-6, d₁₂= - 4,08959962·10^-6, d₁₃= - 0,25614575·10^-6

d₂₁= + 4,08960007·10^-6, d₂₂= 1- 0,84078196·10^-6, d₂₃= +1,73888389·10^-6

d₃₁= + 0,25613964·10^-6, d₃₂= - 1,73888494·10^-6, d₃₃= 1- 0,84077363·10^-6

6. Transformacja: [X, Y, Z]_G => [X, Y, Z]_K

Transformację współrzędnych kartezjańskich [X, Y, Z]_G opartych o elipsoidę GRS-80 na współrzędne [X, Y, Z]_K w układzie kartezjańskim elipsoidy Krasowskiego można przeprowadzić według wzorów:

lub w postaci macierzowej:

gdzie:

T - wektor przesunięć środków układów,

C - macierz parametrów rotacji,

c_ij - elementy macierzy parametrów (i, j = 1, 2, 3).

Zgodnie z instrukcją techniczną G-1.10 parametry macierzy C mają wartości:

c₁₁= 1+ 0,84076440·10^-6, c₁₂= + 4,08960694·10^-6, c₁₃= + 0,25613907·10^-6

c₂₁= - 4,08960650·10^-6, c₂₂= 1+ 0,84076292·10^-6, c₂₃= - 1,73888787·10^-6

c₃₁= - 0,25614618·10^-6, c₃₂= + 1,73888682·10^-6, c₃₃= 1+ 0,84077125·10^-6

Przyjmując, że układy kartezjańskie rozważanych elipsoid mają osie zbliżone do równoległych (odchylenia od równoległości nie przekraczają 1") można przyjąć uproszczenie powyższych wzorów.

Uproszczenie to polega na przyjęciu następujących podstawień:

c₁₁ ≈ c₂₂ ≈ c₃₃ ≈ m, c₁₂ ≈ - c₂₂ ≈ ε_z,

c₁₃ ≈ - c₃₁ ≈ - ε_y, c₂₃ ≈ - c₃₂ ≈ ε_x,

gdzie:

ε_x, ε_y, ε_z - oznaczają kąty obrotów osiowych.

Ostateczne parametry transformacji są następujące:

T_X = - 33,4297 m T_Y = + 146,5746 m T_Z = + 76,2865 m,

m = 1 + 0,8407728 · 10^-6,

ε_x = - 1,7388854 · 10^-6 [rad] = - 0,35867",

ε_y = - 0,2561460 · 10^-6 [rad] = - 0,05283",

ε_z = + 4,0896031 · 10^-6 [rad] = + 0,84354".

7. Korekta post-transformacyjna Hausbrandta

W przypadku, gdy układem pierwotnym lub wynikowym (wtórnym) jest układ "1965" to w świetle Instrukcji Technicznej G-2 oraz Wytycznych Technicznych G-1.10 należy wykonać dodatkową korektę wynikającą z lokalnych odchyleń matematycznego układu "1965" od jego rzeczywistej realizacji przez państwowe osnowy geodezyjne.

Korekta post-transformacyjna Hausbrandta, realizuje usunięcie odchyłek na punktach dostosowania i ich wyrównanie na wszystkich punktach transformowanych.

Korekta polega na tym, że współrzędne punktów dostosowania w układzie wtórnym pozostawia się w takiej postaci, w jakiej były przyjęte do transformacji (inaczej mówiąc, od współrzędnych transformowanych odejmuje się wartości poprawek powracając do wartości współrzędnych katalogowych), natomiast wszystkim pozostałym punktom transformowanym przydziela się poprawki wyznaczone przy zastosowaniu wzorów interpolacyjnych.

6

---