1
Rodzaje Współrzędnych
1) Kartezjańskie
a) na płaszczyźnie
b) w przestrzeni
2) Biegunowe
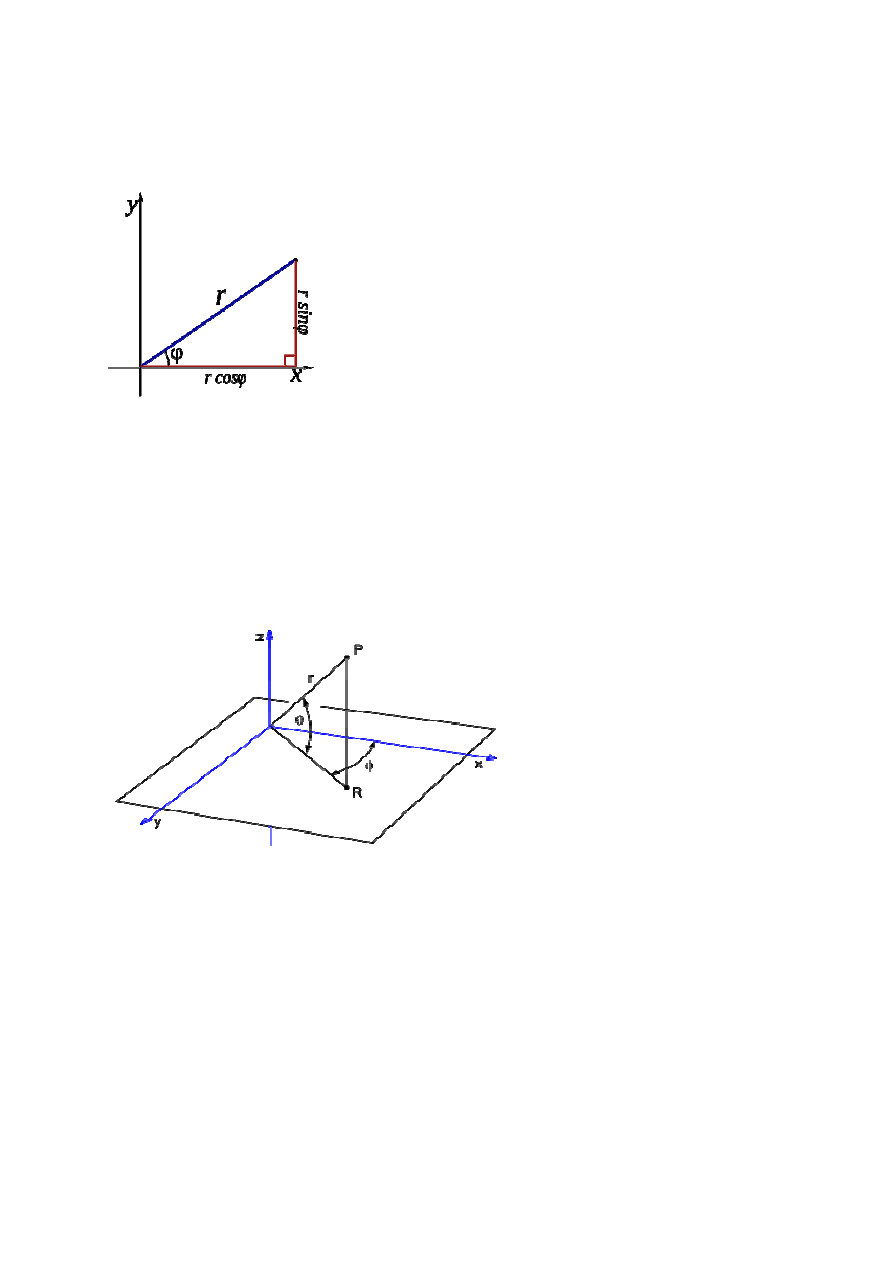
Obieramy na płaszczyźnie dowolny punkt O zwany biegunem i kreślimy półprostą Ox- oś
biegunową.
Aby wyznaczyć położenie punktu P tej płaszczyzny we współrzędnych biegunowych
podajemy długość r odcinka OP oraz kąt
φ
=(Ox,OP)
2
Związek współrzędnych prostokątnych oraz biegunowych jest następujący.
P=P(x
0
,y
0
)=P(r,φ)
x= r cosφ
y= r sinφ
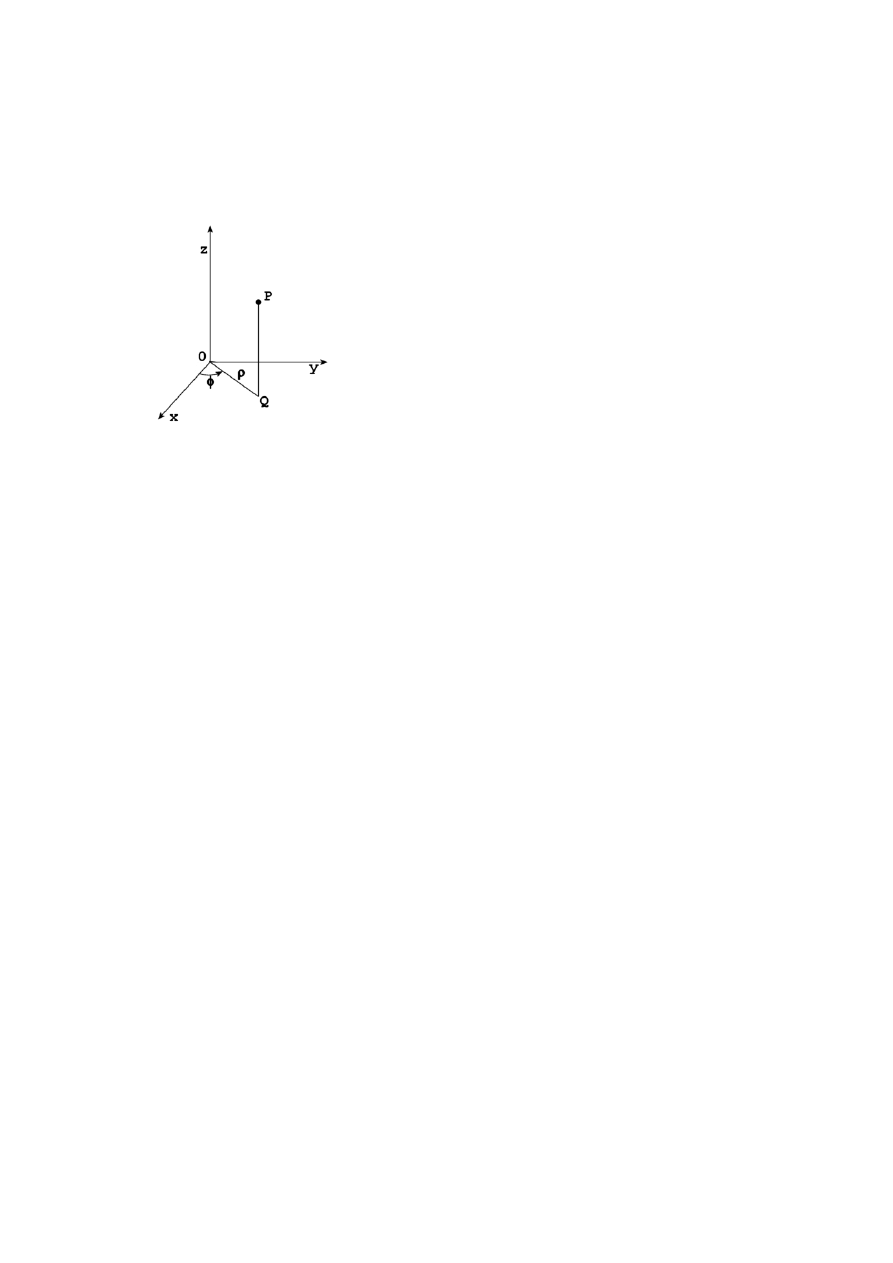
3) Sferyczne-kuliste
Dany jest układ prostokątny 0xyz w przestrzeni. Każdy punkt przestrzeni jest jednoznacznie
wyznaczony przez podanie uporządkowanej trójki liczb rzeczywistych P=P(x
0
,y
0
,z
0
)
Punkt R jest rzutem prostopadłym punktu P na płaszczyznę 0xy.
r=|0P| - odległość punktu P od początku układu współrzędnych 0xyz
Φ= miara kąta skierowanego dodatnio między półosią 0x oraz wektorem 0R
Θ= miara kąta skierowanego dodatnio w półprzestrzeni 0xyz, z ≥0, a ujemnie w
półprzestrzeni 0xyz ,z≤0 między wektorem 0R oraz wektorem 0P
Współrzędnymi sferycznymi lub kulistymi punktu P nazywamy uporządkowaną trójkę (r,Φ,θ)
Pomiędzy współrzędnymi prostokątnymi x
0,
y
0
,z
0
oraz współrzędnymi sferycznymi punktu P
zachodzą związki
x
0
= r cosΦcosθ
y
0
= r sinΦcosθ
z
0
= r sinθ
3
4) Cylindryczne –walcowe
Dany jest układ prostokątny 0xyz w przestrzeni . Współrzędne prostokątne punktu P wynoszą
x
0
,y
0
,z
0
Punkt Q jest rzutem prostopadłym punktu P na 0xy
ρ= |0Q| odległość punktu Q od początku układu współrzędnych
Φ miara kąta skierowanego dodatnio między 0x i wektorem 0Q
h=|QP| odległość P od płaszczyzny 0xy liczone dodatnio dla punktów leżących nad 0xy czyli
dla z≥0, a ujemnie dla punktów leżących pod 0xy czyli dla z≤0
Współrzędnymi cylindrycznymi punktu P nazywamy uporządkowaną trójkę : ρ,Φ,h
Związek między x
0
, y
0
, z
0
oraz ρ,Φ,h jest następujący
x
0
= ρ cosΦ
y
0
= ρ sinΦ
z
0
= h
PRZESTRZENIE METRYCZNE
Mówimy, że zbiór X≠
∅
jest przestrzenią metryczną jeżeli został określony funkcjonał tzn.
funkcja o wartościach liczbowych: rzeczywistych lub zespolonych zwany metryką.
d:XˣX→
ℜ
takich, że dla dowolnych x,y,z
∈
X zachodzą aksjomaty
a) d(x,y)=0↔x=y
b) d(x,y)=d(y,z)
c) d(x,y)≤d(x,z)+d(z,y)
Przestrzenią metryczną oznaczamy symbolem <X,d>. Liczbę d(x,y) nazywamy odległością x
od y.
KULĄ OTWARTĄ
(domkniętą)
o środku p
0
∈
<X,d> i promieniu r>0 nazywamy zbiór
K(p
0
,r)={q
∈
X:d(q,p
0
)<r},
K(p
0
,r)={q
∈
X:d(q,p
0
)≤r}
4
Sąsiedztwem punktu
p
0
∈
<X,d> nazywamy zbiór S(p
0
,r)=K(p
0
,r)\{p
0
}
Kulę otwartą K(p
0
,r) nazywamy również
otoczenie punktu p
0
o promieniu r.
Punkt p
∈
<X,d> nazywamy punktem skupienia zbioru E
⊂
X jeżeli każde otoczenie K(p,r)
zawiera punkt q≠p takie, że q
∈
E.
Dopełnieniem zbioru E
⊂
X nazywamy zbiór E
’
=X\E
Niech E będzie podzbiorem przestrzeni metrycznej <X,d>
a) punkt p
∈
E nazywamy punktem wewnętrznym zbioru E jeżeli istnieje
otoczenie K(p,r)
⊂
E
b) zbiór E nazywamy zbiorem otwartym w <X,d> jeżeli każdy punkt zbioru E
jest jego punktem wewnętrznym
c) zbiór E nazywamy zbiorem domkniętym w <X,d> jeżeli X\E jest zbiorem
otwartym.
Mówimy, że zbiór E jest ograniczony z góry
(
ograniczony z dołu
)
jeżeli:
≥
∀
∃
≤
∀
∃
∈
ℜ
∪
∈
ℜ
∈
y
x
y
x
E
x
y
E
x
y
Jeżeli zbiór E jest ograniczony z góry oraz z dołu to mówimy, że E jest ograniczony.
Niech zbiór E będzie ograniczony z góry. Mówimy, że liczba M
∈
ℜ
jest kresem górnym lub
SUPREMUM
zbioru E jeżeli:
a) M jest ograniczeniem górnym zbioru E
b) jeżeli x<M, to x nie jest ograniczeniem górnym zbioru E; piszemy M=supE
Niech zbiór E będzie ograniczony z dołu. Mówimy, że liczba m
∈
ℜ
jest kresem dolnym lub
INFINIUM
zbioru E jeżeli:
a) m jest ograniczeniem dolnym zbioru E
b) jeżeli x<m, to x nie jest ograniczeniem dolnym zbioru E; piszemy M=infE
−
>
∃
∀
∧
≤
∀
⇔
=
∈
>
∈
ε
ε
M
y
M
x
E
M
E
y
E
x
0
sup
+
<
∃
∀
∧
≥
∀
⇔
=
∈
>
∈
ε
ε
M
y
m
x
E
m
E
y
E
x
0
inf
TWIERDZENIE 1
Każdy nie pusty zbiór A
⊂
ℜ
ograniczony z góry, posiada kres górny supA
∈
ℜ
5
Każdy nie pusty zbiór A
⊂
ℜ
ograniczony z dołu, posiada kres dolny infA
∈
ℜ
PRZESTRZEŃ LICZB ZESPOLONYCH
LICZBĄ ZESPOLONĄ
nazywamy uporządkowaną parę liczb rzeczywistych: a,b.
Oznaczamy je symbolem z=(a,b)
W zbiorze liczb zespolonych ˣ w następujący sposób definiujemy dodawanie i mnożenie.
Niech x=(a,b), y=(c,d)
gdzie a,b,c,d
∈
ℜ
wtedy:
(*)
x=y↔(a=c
∧
b=d)
x+y=(a+c,b+d)
xy=(ac-bd,ad+bc)
TWIERDZENIE 1
Operacja dodawania i mnożenia postaci
(*)
w zbiorze liczb zespolonych ˣ są przemienne,
łączne oraz mnożenie jest rozdzielne względem dodawania, tzn. dla dowolnych liczb
zespolonych x,y,z zachodzą równania
x+y=y+x
x+(y+z)=(x+y)+z
xy=yx
x(yz)=(xy)z
x(y+z)=xy+xz
Dla dowolnej liczby zespolonej x mamy
x+(0,0)=x
x(0,0)=(0,0)
x(1,0)=x
TWIERDZENIE 2
Dla dowolnej liczby zespolonej x istnieje dokładnie jedna liczba zespolona y taka, że
x+y=(0,0)
Jeżeli x+y=(0,0) to piszemy y=-x
Dla x=(a,b) mamy y=(-a,-b)
Niech x=(a,b)
WARTOŚCIĄ BEZWZGLĘDNĄ LUB MODUŁEM LICZBY ZESPOLONEJ
x
nazywamy liczbę nieujemną
2
2
b
a
x
+
=
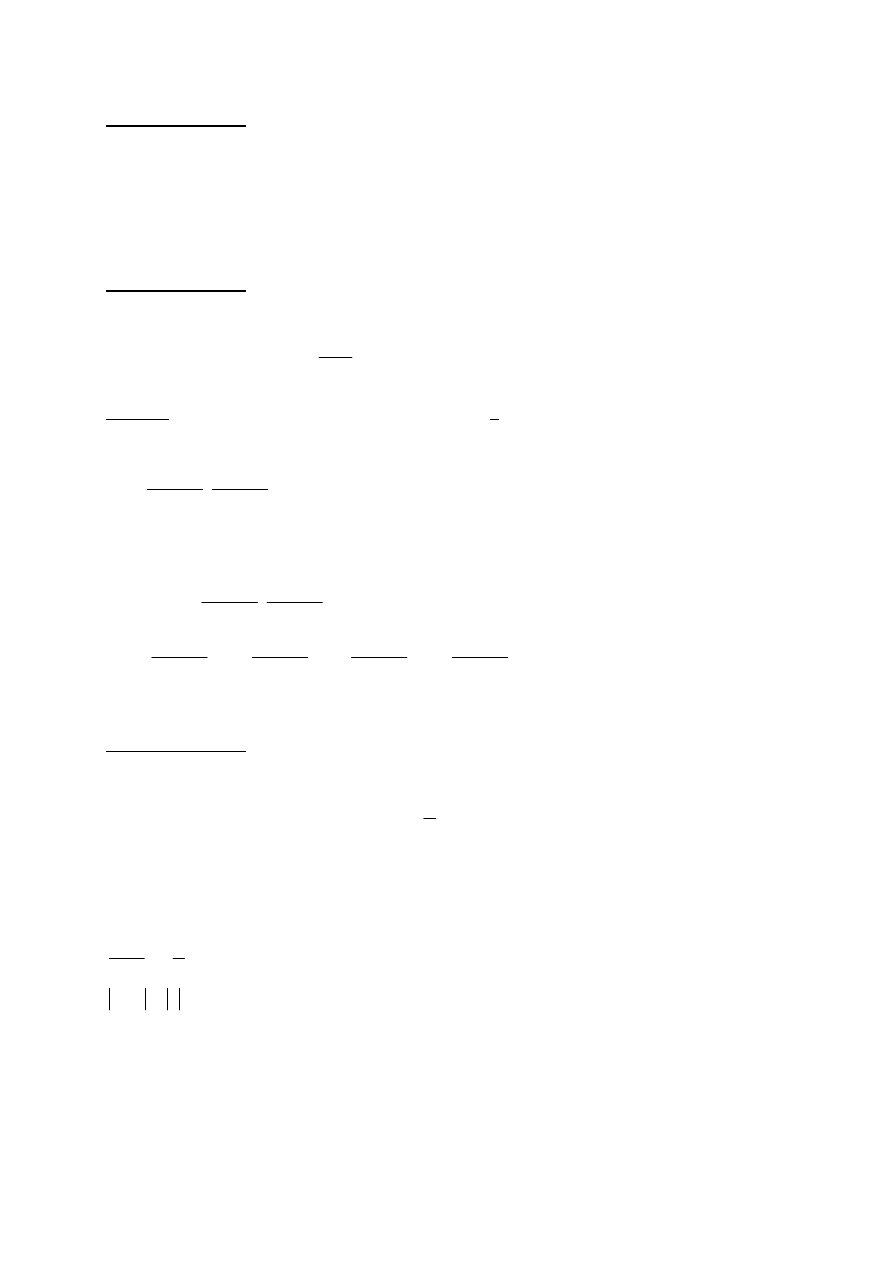
6
TWIERDZENIE 3
Niech x,y,z będą liczbami zespolonymi wtedy:
a) jeżeli x≠(0,0) to |x|>0
b) |xy|=|x||y|
c) jeżeli xy=(0,0) to x=(0,0) y=(0,0) lub x=y=(0,0)
d) jeżeli x≠(0,0) oraz xy=xz to y=z
TWIERDZENIE 4
Dla dowolnej liczby zespolonej x≠(0,0) istnieje dokładnie jedna liczba zespolona y, tak, że
xy=(0,0) piszemy wtedy
x
y
)
0
,
1
(
=
Dowód: Jednoznaczność y wynika z Twierdzenia 3d. Niech x=(a,b) wtedy y określamy
następująco
+
+
=
2
2
2
2
,
b
a
b
b
a
a
y
gdyż
( )
( )
0
;
1
,
,
,
2
2
2
2
2
2
2
2
2
2
2
2
=
=
+
⋅
+
+
−
⋅
+
−
⋅
−
+
⋅
=
=
+
+
=
⋅
b
a
a
b
b
a
b
a
b
a
b
b
b
a
a
a
b
a
b
b
a
a
b
a
y
x
TWIERDZENIE 5
Jeżeli x≠(0,0) to dla dowolnej liczby zespolonej y istnieje dokładnie jedna liczba zespolona z
taka, że xz=y Oznaczamy ją symbolem
x
y
z =
Ponieważ dla dowolnych liczb rzeczywistych a,b zachodzą równości
( ) ( ) (
)
0
,
0
,
0
,
b
a
b
a
+
=
+
( ) ( ) (
)
0
,
0
,
0
,
b
a
b
a
⋅
=
⋅
( )
( )
=
0
,
0
,
0
,
b
a
b
a
jeżeli b≠0
( )
a
a
=
0
,
więc liczbę zespoloną postaci (a,0) można utożsamiać z liczbą postaci „a” oraz traktować
zbiór liczb rzeczywistych
ℜ
jako podzbiór liczb zespolonych ˣ. Przy czym
ℜ
⊆ ˣ
JEDNOSTKA UROJONĄ
nazywamy liczbę zespoloną
i=(0,1)
zauważamy, że i
2
=ii=(0,1)(0,1)=(0-1,0+0)=(-1,0)=-1, czyli i
2
=-1
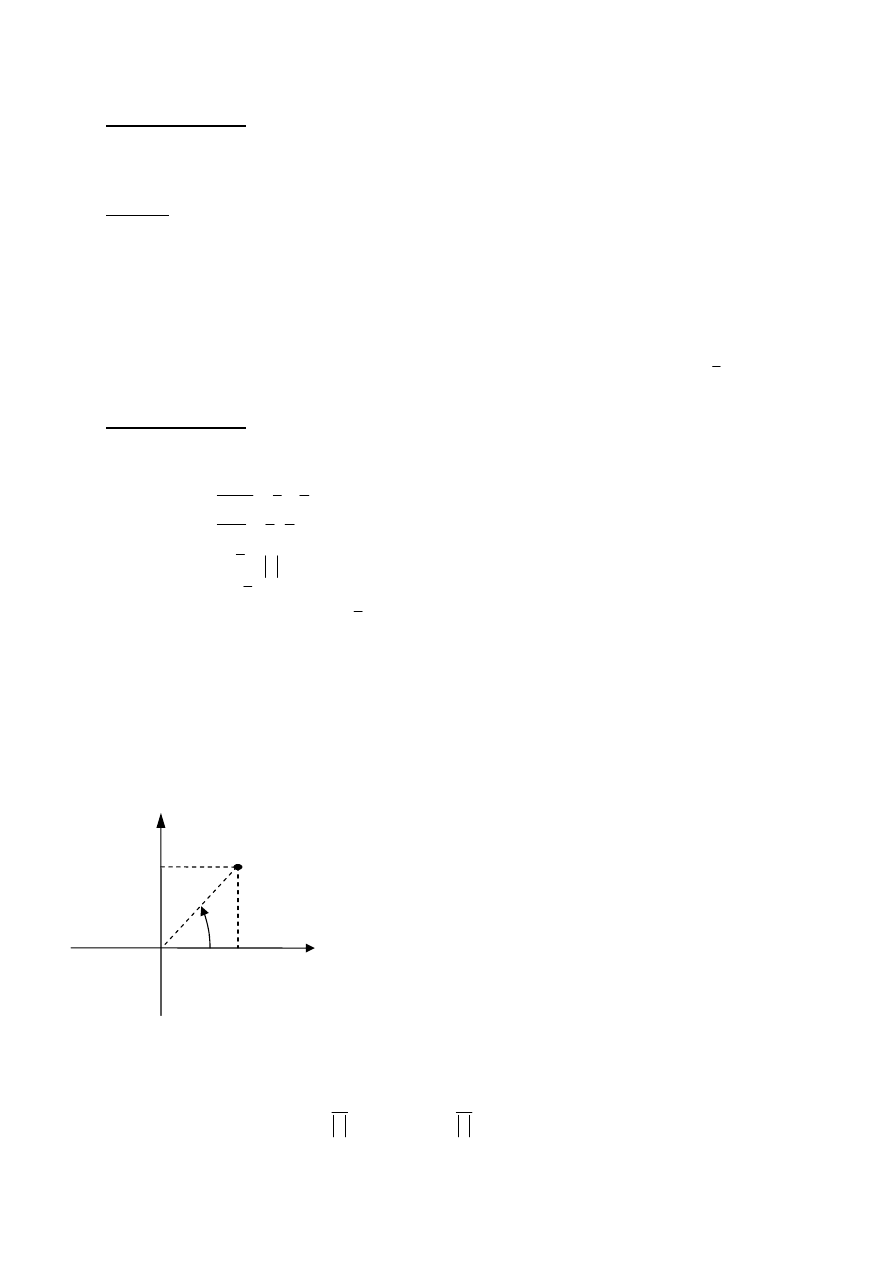
7
TWIERDZENIE 6
Jeżeli a,b
∈
ℜ
to (a,b)=a+bi
Dowód: a+bi=(a,0)+(b,0)(0,1)=(a,0)+(0-0,b+0)=(a,0)+(0,b)=(a,b)
Jeżeli z=a+bi to
„a” nazywamy częścią rzeczywistą z
„b” nazywamy częścią urojoną z
Piszemy
Rez=a
Imz=b
LICZBĄ SPRZĘŻONĄ
z liczbą zespoloną
bi
a
z
+
=
nazywamy liczbę zespoloną
bi
a
z
−
=
TWIERDZENIE 7
Jeżeli x,y
∈
ˣ ,to
a)
y
x
y
x
+
=
+
b)
y
x
y
x
⋅
=
⋅
c)
2
x
x
x
=
⋅
d)
ℜ
∈
=
+
x
x
x
Re
2
e) jeżeli
ℜ
∈
x
to
x
x =
Liczbie zespolonej z=(a,b)=a+bi odpowiada wzajemnie jednoznacznie na płaszczyźnie
prostokątnego układu współrzędnych 0xy punkt (a,b).
Płaszczyznę C, której punktom zostały przyporządkowane liczby zespolone nazywamy
płaszczyzną liczbową.
Punktom osi 0x odpowiadają wzajemnie jednoznacznie liczby zespolone (a,0).
Punktom osi 0y odpowiadają wzajemnie jednoznacznie liczby zespolone (b,0)
ARGUMENTEM LICZBY ZESPOLONEJ
z=a+bi ≠(0,0) nazywamy liczbę rzeczywistą φ
określoną równością
z
a
=
ϕ
cos
oraz
z
b
=
ϕ
sin
|z|
φ
Re{z}
Im{z}
b
a
z=(a,b
)=a+ib
8
piszemy φ=arg z
Każda liczba zespolona z≠(0,0) posiada nieskończenie wiele argumentów.
Jeżeli φ jest argumentem z≠(0,0) to każdy inny argument z ma postać φ+2kπ k
∈
Z
Argument liczby zespolonej z≠(0,0), który spełnia warunek –π<arg z<π nazywamy
argumentem z i oznaczamy symbolem Arg z
Jeżeli z=a+bi≠(0,0) to ponieważ a=|z|cosφ oraz b=|z|sinφ to możemy napisać
z=|z|cosφ+|z|sinφi=|z|(cosφ+isinφ)
postać trygonometryczna liczby z≠(0,0)
jeżeli z=r(cosφ+isinφ) to r=|z| φ=arg z
Jeżeli
z
1
=|z
1
|(cosφ+isinφ) ≠(0,0)
z
2
=|z
2
|(cosψ+isinψ) ≠(0,0)
to
arg(z
1
z
2
)=argz
1
+argz
2
arg(z
1/
z
2
)=argz
1
-argz
2
TWIERDZENIE 8
Dla każdej liczby zespolonej z≠(0,0) zachodzi równanie arg(z
n
)=n argz n=1,2…
oznacza to że dla dowolnego argumentu argz istnieje taki argument arg(z
n
) , że zachodzi
równość arg(z
n
)=n argz
Wniosek
WZÓR
DE MOIVRE’A
(cosφ+isinφ)
n
=cos(nφ)+isin(nφ) n=1,2….
TWIERDZENIE 9
Jeżeli
z=|z|(cosφ+isinφ) ≠(0,0)
to istnieje dokładnie n różnych pierwiastków W
k
( k=1,2…n-1 ) n-tego stopnia liczby
zespolonej przy czym
+
+
+
=
n
k
i
n
k
z
W
n
k
π
ϕ
π
ϕ
2
sin
2
cos
dla k=0,1,2…n-1, gdzie
n
z oznacza pierwiastek