Podział sygnałów

Wśród sygnałów ciągłych wyróżniamy:

• Ograniczone co do wartości, to takie których wartości liczbowe w całym zakresie zmiennej niezależnej n nie przekraczają pewnej liczby

• O skończonym czasie trwania, do których zaliczymy sygnały różne od zera w ograniczonym przedziale czasu oraz równe zeru dla czasu spoza tego przedziału

• O ograniczonym widmie, to zbiór sygnałów, których widmo X(jw) jest ograniczone pewną stałą W.

Widmo sygnału - transformata Fouriera sygnału x[n] 

* Sygnały dzielimy także ze względu na ich przeciwdziedzinę (zbiór wartości). Jeżeli zbiór ten jest ciągły, sygnał nazywamy ciągłym w amplitudzie. Jeżeli jest on dyskretny (w szczególności skończony) sygnał nazywamy dyskretnym w amplitudzie.

Łącząc kryteria podziału sygnałów ze względu na rodzaj ich dziedziny i przeciwdziedziny, można wyodrębnić cztery klasy sygnałów:

* z czasem ciągłym i ciągłe w amplitudzie

* z czasem ciągłym i dyskretne w amplitudzie

* z czasem dyskretnym i ciągłe w amplitudzie

* z czasem dyskretnym i dyskretne w amplitudzie (cyfrowe).

W klasie sygnałów dyskretnych wyróżniamy sygnały binarne, które przybierają w każdej chwili tylko dwie wartości binarne (np. 0 i 1 lub 1 i -1 ).

Reprezentacja sygnałów:

* transformata Fouriera (widmo sygnału)

* transformata Laplace'a

* szereg Kotielnikowa-Shannona

* sygnał analityczny

Sygnał dyskretny może mieć skończona lub nieskończoną długość. Sygnał dyskretny o skończonej długości zawiera się w przedziale od N1 do N2, przy czym N2 >N1. Czas trwania sygnału wyznaczamy jako: N=N2-N1+1.

 Sygnały dyskretne dzielimy na:

-Sygnały kwantowane w pionie

-Sygnały kwantowane w poziomie

-Sygnały cyfrowe

Digitalizacja - przetwarzanie sygnału ciągłego (analogowego) na sygnał dyskretny (cyfrowy). Sygnał analogowy, będący funkcją ciągłą określonego parametru (np. napięcia, temperatury itp.), najczęściej względem czasu, podlega próbkowaniu, tzn. jego wartość mierzona jest w bardzo krótkich odstępach czasu.

Pełny zakres wartości sygnału dzielony jest na przedziały (operacja kwantowania, kwantyzacji), którym przypisywane są kody liczbowe, tzw. słowa kodowe, zapisywane zwykle w systemie dwójkowym (binarnym).

Sygnały w postaci dyskretnej mogą być przesyłane w sposób pewny, z wyeliminowaniem zniekształceń i możliwości zagubienia sygnałów małej mocy w tzw. szumach; mogą też być magazynowane i analizowane w systemach komputerowych oraz wykorzystywane w urządzeniach cyfrowych, a także - po przetworzeniu ponownie na sygnały ciągłe - wykorzystywane w urządzeniach analogowych.

Energia sygnału jest energią zawartą w sygnale x może ona być nieskończona lub nieokreślona dla pewnej klasy sygnałów. Jeżeli sygnał x jest sygnałem prądowym lub napięciowym, to całka ma interpretację energii wydzielonej przez sygnał na rezystorze jednostkowym. W przypadku innych sygnałów (akustycznych lub optycznych), można mówić o uogólnionym pojęciu energii.

Energia, moc średnia i wartość skuteczna, należą do najważniejszych parametrów sygnału. Wielkości te są nazywane parametrami energetycznymi sygnałów. Ponieważ założyliśmy, że sygnały są wielkościami bezwymiarowymi, ich energię wyrażamy w sekundach, moc zaś oraz wartość skuteczna są bezwymiarowe.

Na podstawie parametrów energetycznych dokonujemy jeszcze jednego ważnego podziału sygnałów na dwie klasy: klasę sygnałów o ograniczonej energii oraz klasę sygnałów o ograniczonej mocy.

* moc sygnałów o ograniczonej energii jest równa zeru,

* energia sygnałów o ograniczonej mocy jest nieskończona,

* każdy sygnał impulsowy ograniczony w amplitudzie jest sygnałem o ograniczonej energii,

* sygnały o nieskończonym czasie trwania mogą być sygnałami o ograniczonej energii bądź o ograniczonej mocy,

* sygnały o ograniczonej mocy i ograniczone w amplitudzie są sygnałami o nieskończonym czasie trwania,

* szczególną podklasą tych ostatnich są sygnały okresowe.

Sygnały o skończonej energii, E<∞. Takie sygnały muszą mieć zerową moc średnią - sygnał energii. Przykładem sygnału o skończonej energii i zerowej mocy jest sygnał bramki.

Sygnały o skończonej mocy średniej i nieskończonej energii. Jeśli sygnał niesie niezerową moc średnią, to w nieskończonym przedziale czasu uzyskamy nieskończoną ilość energii. Przykładem takiego sygnału jest każdy sygnał stały oraz sygnały okresowe - sygnał mocy, np. sygnał stały x[n]=4, którego moc średnia wynosi 16, zaś energia jest nieskończenie duża.

Sygnały, których moc i energia mają w nieskończonym przedziale czasu nieskończoną wartość.

Transformacje sygnału w dziedzinie zmiennej niezależnej:

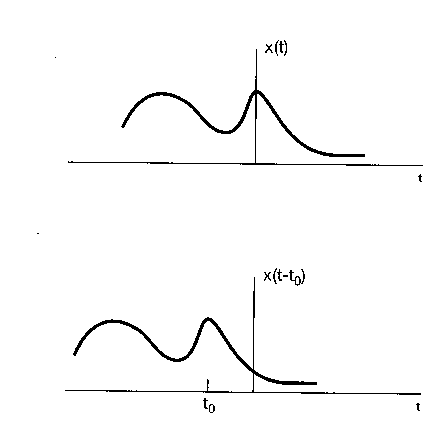
-Przesunięcie w czasie, zwane przesunięciem fazowym - sygnały opóźnione i  wyprzedzające (y[n]=x[n-no] - w zależności od znaku no system wprowadza opóźnienie -no>0 lub przyspieszenie no<0)

-Odwrócenie sygnału w dziedzinie czasu (odbicie względem początku układu współrzędnych) y[n]=x[-n]

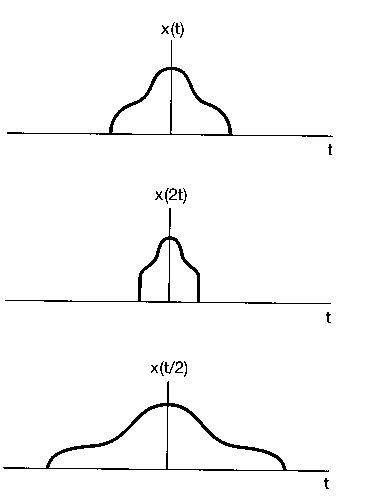
-Skalowanie sygnału w dziedzinie czasu (x[2n] - sygnał skompresowany, x[n/2] - sygnał rozciągnięty

W ogólnym przypadku transformacji sygnału obejmującym trzy powyższe operacje zapiszemy: x[an+b], gdzie dla |a|>1 otrzymamy sygnał liniowo skompresowany (ściśnięty), dla 0<|a|<1 sygnał liniowo rozciągnięty w czasie, dla a<0 uzyskamy odwrócenie sygnału w czasie; wartość i znak b decydują o przesunięciu fazowym sygnału.

Sygnały impulsowe o ograniczonej energii

Sygnały o nieskończonym czasie trwania i o ograniczonej energii

Sygnały o ograniczonej mocy średniej - nieokresowe

•Sygnały są fizyczną reprezentacją wiadomości

•Są nośnikiem informacji przekazywanych na dowolne odległości

•Powstają w nadajnikach (koderach)

•Przesyłane są przez kanał telekomunikacyjny

-czas trwania, który może być ograniczony jakimś przedziałem czasowym, formalnie przedstawionym jako różnica pomiędzy końcem przedziałuT2 i początkiem przedziału T1,

-wartość chwilową sygnału, mierzoną w jednostkach właściwych dla danej wielkości,

- funkcję opisującą przebieg sygnału, przy czym sygnał może być funkcją jednej zmiennej lub wielu zmiennych niezależnych,

- specyficzne własnościopisujące naturę danego sygnału, takie jak: amplituda, częstotliwość, energia, moc, okresowość, itp.

Sygnał analogowy:

Klasyfikacja sygnałów:

- ograniczone co do wartości - takie których wartości liniowe w całym zakresie zmiennej niezależnej n nie przekraczają pewnej liczby,

- o skończonym czasie trwania - do których zaliczamy sygnały różne od zera w ograniczonym przedziale czasu oraz równe zeru dla czasu spoza tego przedziału,

- o ograniczonym widmie - zbiór sygnałów, których widmo X(jω) jest ograniczone pewną stałą W.

(symetryczny unormowany impuls prostokątny o jednostkowym czasie trwania i jednostkowej amplitudzie; jego wartość średnia i energia są również równe jedności; symbol Π(t)) - dowolny impuls prostokątny o wysokości a, szerokości b, przesunięty względem zera o czas c: aΠ[(t-c)/b],

czas trwania impulsu trójkątnego Λ(t), jest z definicji równy 2

Sygnał x(t), jest dowolnym sygnałem impulsowym (często prostokątnym) i jest nazywany obwiednią sygnału y(t), a sygnał cos(ω t+φ) - jego wypełnieniem.

Sa

Sax=(sinx)/x

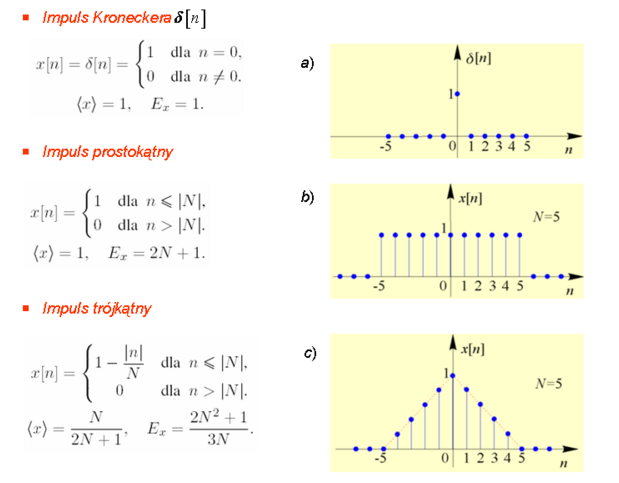
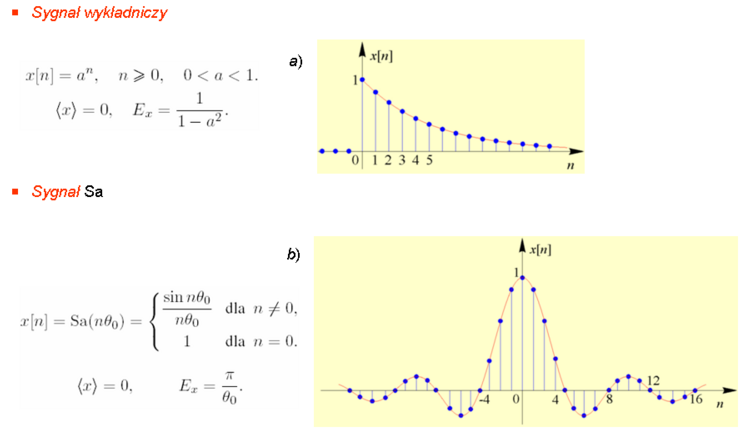
Sygnały przedstawione na rys. a)-d) są przykładami prostych sygnałów o nieskończonym czasie trwania i ograniczonej mocy (ich energia jest nieskończona).

Sygnał skoku jednostkowego 1(t)

Zapis X0(t-t0)\, oznacza skok o wartość X0 w chwili t0

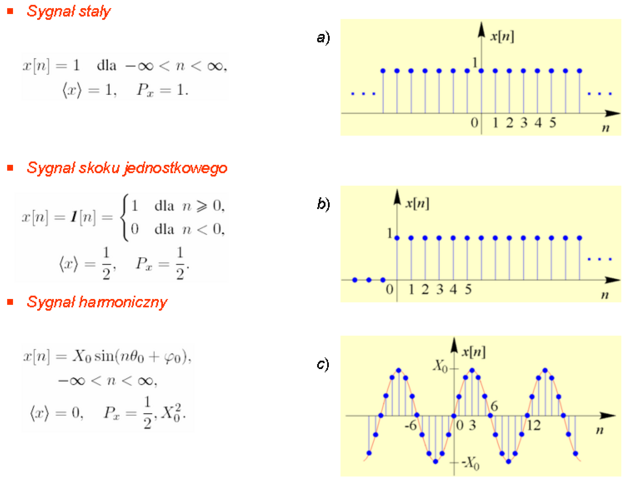
Na rys. a), b) i c) są pokazane przykłady najczęściej spotykanych sygnałów okresowych. Są to oczywiście sygnały o ograniczonej mocy. Pełnią one w praktyce rolę sygnałów nośnych w różnych systemach modulacji sygnałów, a także sygnałów synchronizujących.

Sygnał harmoniczny (rys. a) jest określony przez trzy parametry: amplitudę X0 , pulsację ω0 (lub częstotliwość f0=ω0/2π=1/T0 , gdzie T0\, jest okresem), oraz fazę początkową φ0 . Jest on wykorzystywany m.in. jako fala nośna w analogowych systemach modulacji.

Fala prostokątna bipolarna (rys. b) jest wykorzystywana jako przebieg synchronizujący i zegarowy, zaś fala prostokątna unipolarna (rys. c) jako przebieg nośny w impulsowych systemach modulacji.

Funkcje

noszą nazwę modułu i odpowiednio argumentu sygnału z(t). Są to funkcje rzeczywiste czasu.

Sygnały zespolone również dzielimy na sygnały o ograniczonej energii i sygnały o ograniczonej mocy. W przypadku sygnałów zespolonych we wzorach definiujących energię i moc lub należy w wyrażeniu podcałkowym uwzględnić nie kwadrat sygnału x^2(t) , a kwadrat modułu sygnału |x^2(t)|.

Sygnał harmoniczny zespolony (1.11) nazywany także sinusoidą zespoloną, jest często wykorzystywany do reprezentacji rzeczywistego sygnału harmonicznego x(t)=cosω0 t , przy czym x(t)=Re z(t) . Jest to oczywiście sygnał o ograniczonej mocy. Jego moc, jak można łatwo sprawdzić jest równa 1.

SYGNAŁ SINUSOIDALNY

U = A sin 2 π ft

gdzie:

A - Amplituda

f - częstotliwość

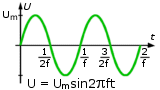
Amplituda - nieujemna wartość określająca wielkość przebiegu funkcji okresowej

Amplituda A w przebiegach sinusoidalnych jest maksymalną wartością tego przebiegu:

Czasami zamiast amplitudy używa się pojęcia wartości skutecznej Usk czy też wartości międzyszczytowej Upp.

Wartość skuteczna jest równa Usk=0,707*Um, natomiast wartość międzyszczytowa jest równa podwojonej amplitudzie Upp=2Um.

Częstotliwość określa liczbę cykli zjawiska okresowego występujących w jednostce czasu. W układzie SI jednostką częstotliwości jest herc (Hz).

Częstotliwość 1 herca odpowiada występowaniu jednego zdarzenia (cyklu) w ciągu 1 sekundy. Najczęściej rozważa się częstotliwość drgań, częstotliwość napięcia, częstotliwość fali.

f=1/T,

gdzie:T- okres,

f - częstotliwość,

f=ω/2π

gdzie: ω - pulsacja.

U = A sin (2 π ft + φ)

gdzie φ oznacza fazę

Faza sygnału - faza drgań wywołanych ruchem falowym.

Jest to wielkość skalarna wyrażona w radianach, która określa w której części fali okresu znajduje się punkt fali.

O(A) oznacza sygnał wejściowy przy sterowaniu wejścia sygnałem A to układ jest liniowy jeżeli

O(A)+O(B)=O(A+B)

Odpowiedzią układu liniowego na doprowadzony do wejścia sygnał sinusoidalny jest również sygnałem sinusoidalnych chociaż ze zmienioną fazą i amplitudą. Żaden inny sygnał nie ma tej własciwości

• Impuls Diraca

• Okresowy ciąg impulsów Diraca (dystrybucja grzebieniowa)

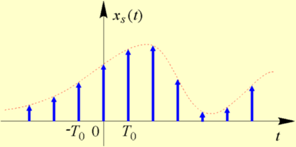
• Impulsowy sygnał spróbkowany

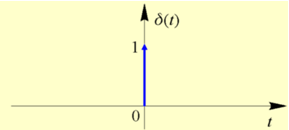
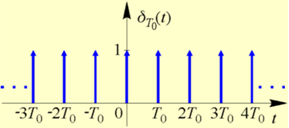
Impuls Diraca δ(t) (rys. a), nazywany również dystrybucją lub deltą Diraca, jest matematycznym modelem nierealizowalnego fizycznie, nieskończenie wąskiego impulsu występującego w chwili t=0 , o nieskończenie dużej amplitudzie i polu równym 1. Z formalnego punktu widzenia jest to sygnał o nieograniczonej mocy! Zapis X0δ(t-t0) oznacza impuls Diraca występujący w chwili t0 o polu równym X0\,

Za pomocą dystrybucji grzebieniowej (nazywanej w literaturze także dystrybucją sza lub comb) można w sposób wygodny zapisać formalnie operację próbkowania równomiernego sygnału jako iloczyn tego sygnału i dystrybucji δT0, . W efekcie otrzymujemy tzw. impulsowy sygnał spróbkowany (1.14) pokazany na rys. d). Sygnał ten stanowi dystrybucyjną reprezentację sygnału spróbkowanego.

Właściwości impulsu Diraca

• Właściwości próbkowania

• Właściwości filtracji

• Związki ze skokiem jednostkowym

• Właściwości splotu

Zgodnie z właściwością (1.15), w wyniku mnożenia sygnału x(t) przez impuls Diraca δ(t-t0) występujący w chwili t0 wyodrębniamy niejako z całego sygnału x(t) jego wartość (próbkę) x(t0) w chwili t0 , którą reprezentujemy impulsem Diraca delta(t-t0) o polu równym x(t0) . Inaczej mówiąc, impuls x(t0)δ(t-t0) stanowi reprezentację dystrybucyjną próbki x(t0) .

# Właściwość filtracji (1.16) wynika natychmiast w właściwości (1.15) i definicji dystrybucji Diraca.

# Całka impulsu Diraca w granicach od -∞, do t jest równa sygnałowi skoku jednostkowego. Pochodna skoku jednostkowego jest równa impulsowi Diraca. Związki te należy jednak rozumieć w sensie dystrybucyjnym.

Splot sygnału x(t) z impulsem Diraca δ(t) daje w wyniku ponownie sygnał x(t). Oznacza to, że delta(t) jest elementem identycznościowym operacji splotu. Splot sygnału x(t) z impulsem Diraca przesuniętym o czas t0 daje w wyniku niezmienioną kopię tego sygnału przesuniętą o ten sam czas.

Właściwości dystrybucji grzebieniowej

• Właściwości próbkowania

• Właściwości powielania okresowego

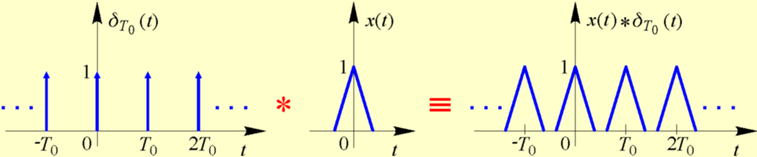
W wyniku splecenia sygnału x(t) z dystrybucją grzebieniową δT0(t) powstaje sygnał, który jest przedłużeniem okresowym sygnału x(t) z okresem T0 . Jeśli sygnał x(t) jest sygnałem impulsowym o czasie trwania mniejszym bądź równym T0, to przedłużenie to jest ciągiem dokładnych kopii sygnału x(t) powtarzanych co odcinek czasu T0 . W przeciwnym przypadku powielone kopie nakładają się na siebie i w sygnale przedłużonym okresowo nie jest zachowany kształt sygnału x(t) .

• Wartość średnia

- Sygnału impulsowego określonego na odcinku [n1,n2]

- Sygnału o nieskończonym czasie trwania

- Sygnału okresowego o okresie No

Sygnały dyskretne - Parametry

• Energia

• Moc średnia

• Moc średnia sygnału okresowego o okresie No

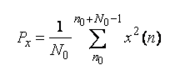
• Wartość skuteczna

---