WYDZIAŁ INŻYNIERII LĄDOWEJ	Dzień/godz.: Poniedziałek, 14.15 - 17.00		Nr zespołu 3
		Data: 01.12.2008r.
Nazwisko i imię	Ocena z przygotowania	Ocena ze sprawozdania	Ocena
1. Głuchowski Łukasz
2. Harakop Paweł
2. Kieras Szymon
Prowadzący: mgr inż. Krzysztof Wieja		Podpis prowadzącego:

Wyznaczanie dyspersji optycznej pryzmatu metodą pomiaru kąta najmniejszego odchylenia.

Cel doświadczenia:

Celem doświadczenia jest obliczenie wartości kąta łamiącego pryzmat, znalezienia kąta minimalnego odchylenia pryzmatu, udowodnienie zjawiska dyspersji optycznej oraz obliczenia jej wartości

Podstawy teoretycznie:

Dyspersja optyczna to zjawisko polegające na zmianie kąta odchylenia w pryzmacie ze względy na długość fali świetlnej padającej na ten pryzmat.

Na skutek dyspersji bezwzględny współczynnik załamania danego ośrodka również zależy od częstości przechodzącego przezeń światła. Charakter dyspersji światła w danym ośrodku określa postać funkcji n= f(ν) lub n= f( λ ).

Zjawisko załamania się światła występuje podczas przechodzenia wiązki światła przez granicę dwóch ośrodków ( rys.)

Kąt jaki tworzy z normalną fala padająca jest równy kątowi fali odbitej. Doświadczalnie stwierdzono że, jeśli ośrodek 1 jest optycznie rzadszy od ośrodka 2, wówczas kąt załamania β jest mniejszy od kąta padania α ( załamanie do normalnej ) oraz ϑ₁ > ϑ₂ . Gdy zaś ośrodek 1 jest optycznie gęstszy od ośrodka 2, promień załamuje się od normalnej i wówczas α < β oraz ϑ₁ < ϑ_{2 .}

Bezwzględny współczynnik załamania jest to stosunek prędkości C światła w próżni do prędkości ϑ

światła w ośrodku do którego wchodzi.

Względny współczynnik załamania jest to stosunek sinusa kąta padania α do sinusa kąta załamania β i równy jest stosunkowi prędkości ϑ₁ i ϑ₂ światła w danych dwóch ośrodkach :

Pryzmat - bryła z materiału przezroczystego dwóch o co najmniej dwóch ścianach płaskich nachylonych do siebie pod kątem ostrym. Używany w optyce do zmiany kierunku biegu fal świetlnych, a poprzez to, że zmiana kierunku zależy od długości fali jest używany do analizy widmowej światła. Charakterystyczne cechy to kąt łamiący pryzmat oraz kat odchylenia w pryzmacie. Kąt odchylenia w pryzmacie przyjmuje swoja wartość najmniejszą, gdy promień wewnętrzny pryzmatu biegnie równolegle do podstawy.

Spektrometr optyczny, przyrząd służący do otrzymywania i analizowania widm promieniowania świetlnego (od podczerwieni do ultrafioletu). Najczęściej stosuje się spektrometry optyczne, które tworzą widma w ten sposób, że światło o różnych długościach fali kierowane jest pod różnym kątem. Składa się on z kolimatora (zamienia on rozbieżną wiązkę światła na równoległą) , rurki z przesłoną i szczeliną oraz obrotowego stolika na którym montuje się pryzmat . w skład spektrometru wchodzi również kątomierz wyposażony w noniusz.

Doświadczenie nr. 1: (Źródłem światła jest lampa sodowa)

Doświadczenie to polega na wyznaczeniu kąta łamiącego pryzmat Metoda ta polega na wykorzystaniu prawa optyki geometrycznej dotyczącego zjawiska odbicia światła.

W tym celu rzucamy wiązkę promieni skierowaną na kąt łamiący i badamy odchylenie odbitych strumieni światła.

Doświadczenie nasze uprzedza czynność ustawienia najmniejszej, ostrej i dobrze widoczniej szczeliny w spektrometrze. Jeżeli wszystkie czynności zostały wykonane prawidłowo to po obu stronach pryzmatu powinniśmy zobaczyć dwie wiązki odbite od jego ścianek (rys.).

Po zatrzymaniu lunety na zlokalizowanej szczelinie, zakręcamy śrubę i odczytujemy z kątomierza wynik ( pamiętamy o tym by przy odczytywaniu wyników nie używać na zmianę kątomierza A i B, tylko by przed pomiarami zdecydować, który będzie przez nas używany)

Słuszność tych pomiarów można udowodnić wyprowadzając po kolei następujące wzory:

a-b=2π-2α-2β

a,b - wskazania kątomierza

α,β - kąty w pryzmacie pomiędzy promieniem wchodzącym i wychodzącym do ich normalnych

i

czyli

	Wartość w położeniu A	Wartość w położeniu B	A-B	Wartość kąta łamiącego pryzmat
Stopnie
Radiany	6,8301	4,7368	2,0933	1,0467

Obliczanie błędu bezwzględnego:

Δϕ= dokładność odczytu + szerokości kątowej obrazu szczeliny =
+
=
=0.00087266 [rad]

Ostatecznie wartość kąta łamiącego wynosi
+/-
(domyślamy się że rzeczywisty kąt wynosi
).

Doświadczenie nr. 2 (lampa neonowa)

Poszukujemy miejsca minimalnego odchylenia promienia wychodzącego z pryzmatu w stosunku do promienia wchodzącego do pryzmatu. W tym celu przekręcamy pryzmat i lunetę jednocześnie, aż do momentu gdy szczelina osiągnie swoje położenie maksymalne i zacznie się cofać. Zaobserwowane zjawisko przedstawia poniższa tabela

TABELA 2 - Kąt najmniejszego odchylenia

LP.

Czerw.

Pomara.

Pomara.

Pom.-Żół.

Żółty

Jasn. Ziel

Jasn. Ziel

Jasn. Ziel

Zielony

Niebieski.

Fiolet.

Stopnie

Odczyt - luneta α

100°20'

101°00'

101°02'

101°06'

101°22'

102°02'

102°08'

102°10'

102°24'

103°46'

104°24'

Odczyt kierunek 0 β

42°46'

42°46'

42°46'

42°46'

42°46'

42°46'

42°46'

42°46'

42°46'

42°46'

42°46'

Radiany

Odczyt - luneta α

1,75115

1,76278

1,76336

1,76453

1,76918

1,78082

1,78256

1,78314

1,78722

1,81107

1,82212

Odczyt kierunek 0 β

0,74642

0,74642

0,74642

0,74642

0,74642

0,74642

0,74642

0,74642

0,74642

0,74642

0,74642

Obliczam błąd bezwzględny pomiaru kąta najmniejszego odchylenia

Δ
=
=0.02036 [rad]

Obliczam współczynnik załamania poszczególnych fal

TABELA 3 - Współczynnik załamania nλ
		Czerw.		Pomara.		Pomara.	Pom.-Żół.		Żółty		Jasn. Ziel		Jasn. Ziel		Jasn. Ziel		Zielony		Niebieski.		Fiolet.
εmin	Stopnie	57°34'		58°14'		58°16'	58°20'		58°36'		59°16'		59°22'		59°24'		59°38'		61°00'		61°38'
		Radiany	1,00473		1,01636		1,01694	1,01811		1,02276		1,03498		1,03615		1,03673		1,04080		1,06465		1,07570
		St.	59°58'
		Rad.	1,0467
n		1,71091	1,71691		1,71721			1,71781		1,72020		1,72640		1,72700		1,72729		1,72934		1,74122	1,74664

Błąd współczynnika n_λ wyznaczamy metodą różniczki zupełnej

TABELA 4 - Współczynnik załamania nλ , wraz z Δn
	Czerw.	Pomara.	Pomara.	Pom.-Żół.	Żółty	Jasn. Ziel	Jasn. Ziel	Jasn. Ziel	Zielony	Niebieski.	Fiolet.
n	1,71091	1,71691	1,71721	1,71781	1,72020	1,72640	1,72700	1,72729	1,72934	1,74122	1,74664
Δn	0,01140	0,01131	0,01131	0,01130	0,01126	0,01116	0,01115	0,01115	0,01111	0,01092	0,01083

Wykres krzywej dyspersji

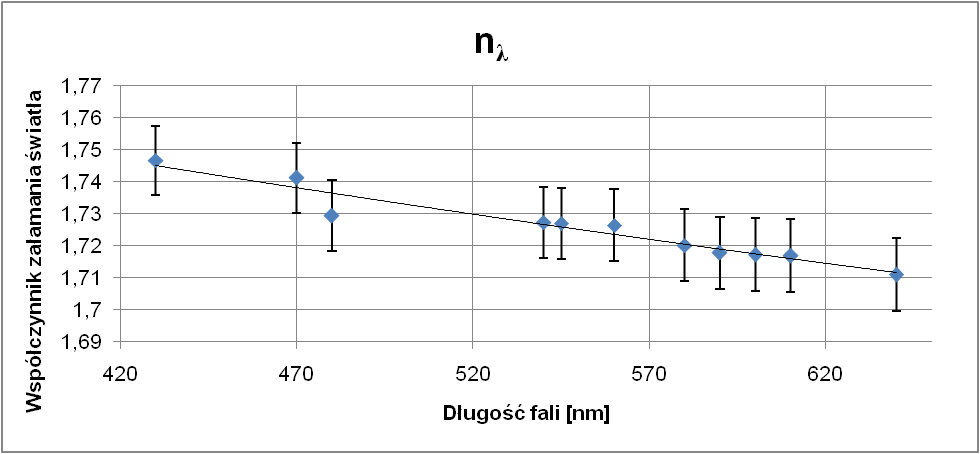
Wartością dyspersji jest różnica największej i najmniejszej wartości współczynników załamania

[Dn] = 1,74664±0,01083-1,71091±0,01140=0,03573 ± 0,02223

Podsumowanie:

Dogłębne zapoznanie się ze zjawiskiem dyspersji, ugięcia i załamania fali. Światło, które widzimy posiada złożoną budowę i składa się z promieni o różnych długościach fal. Różnice między wynikami uzyskanymi doświadczalnie a tymi z tablic należy tłumaczyć dużą niedokładnością pomiarów wynikającą z błędów popełnianych podczas odczytu danych. Wyniki zamieszczone w sprawozdaniu są obarczone błędem wynikającym z występowania wielu odcieni jednej barwy, niedokładności ludzkiego oka, niedokładności sprzętu oraz jego ustawień

---