Wyznaczanie dyspersji optycznej pryzmatu metodą pomiaru kąta najmniejszego odchylenia.

Wydział Matematyki i Nauk Informatycznych	Dzień/godz. wtorek/17:00-20:00		Nr zesp. 9
Temat	Wyznaczanie dyspersji optycznej pryzmatu metodą pomiaru kąta najmniejszego odchylenia.
Data	16.04.2002
Nazwisko i Imię 1. Makarevskaya Marina 2. Mrozowski Jarosław 3. Zielińska Agnieszka	Ocena z przygotowania	Ocena ze sprawozdania	Ocena
Prowadzący: Dr Michał Urbański imię i nazwisko		Podpis prowadzącego

1. Podstawy fizyczne potrzebne do przeprowadzenia ćwiczenia.

Aby zrozumieć zjawisko dyspersji należy najpierw zająć się zjawiskiem załamania światła. Przejawia się ono tym, że światło po przejściu granicy dwóch ośrodków zmienia kierunek swego biegu. Gdy światło pada na granicę dwóch ośrodków, pojawia się wiązka załamana (w ośrodku drugim), oraz wiązka odbita w tym samym ośrodku. W tej chwili interesuje nas jedynie wiązka załamana. Gry światło pada pod kątem α do normalnej do powierzchni granicy dwóch ośrodków, to wiązka załamana biegnie pod kątem β do tejże normalnej. Kąty te spełniają następującą zależność:

sin α / sin β = v1 / v2 = n21 = n1 / n2 ,

gdzie v1, v2 są prędkościami rozchodzenia się załamywanej fali w graniczących ośrodkach, a n21 jest współczynnikiem załamania przy przejściu z ośrodka 1 do 2.

Przy dalszych rozważaniach wykorzystam zasadę Feramata, mówiącą że promień świetlny biegnący z punktu A do punktu B potrzebuje na pokonanie tej drogi albo minimum czasu, albo maksimum czasu.

Powyższe rozważania można ująć wzorem:

∫ n * ds. = extremum ,

gdzie n - bezwzględny współczynnik załamania światła, będący ilorazem : n = c / v (c - prędkość światła w próżni, v - prędkość w ośrodku, do którego wchodzi promień świetlny), oraz s - droga geometryczna.

Iloczyn L = n * s nazywamy drogą optyczną.

Tak więc, zgodnie z zasadą Fermata, przy poruszaniu się światła optymalizowana jest droga optyczna.

Rozważając przypadek załamania światła oraz jego drogę od A przez P - punkt załamania na granicy ośrodków, aż do punktu B i oznaczając drogę AP jako s1 i PB jako s2 możemy powiedzieć, że czas potrzebny na przebycie drogi A-P-B wynosi:

t = s1/v1 + s2/v2 ,

a ponieważ L=n*s to otrzymujemy:

t = (n1*s1 + n2*s2) / c = L / c ,

gdzie L = L1 + L2 - suma dróg optycznych przebywanych w ośrodkach 1 i 2.

Na podstawie zasady Fermata L musi być optymalne zatem:

DL / dx = 0 ,

Gdzie x - punkt na osi OX, gdzie następuje załamanie wiązki.

Oznaczając a - odległość punktu A od osi OX oraz b - odległość B od OX, po prostych przekształceniach otrzymamy zależność:

n1*x / sqr(a² + x²) = n2*(d-x) / sqr(b² + (d-x)²) ,

a następnie:

n1 * sin α = n2 * sin β .

Równanie to opisuje prawo załamania wiązki światła na granicy dwóch ośrodków.

Współczynnik załamania światła w danym ośrodku zależny jest od częstotliwości fali świetlnej. Zjawisko to nazywamy właśnie dyspersją światła oznaczaną Dn. Jest to wielkość charakterystyczna dla materiału.

W obszarach widmowych, dla których dana substancja jest przezroczysta obserwujemy wzrost współczynnika załamania wraz ze wzrostem częstotliwości, natomiast w obszarze widma, dla którego substancja jest nie przezroczysta obserwujemy jego spadek wraz ze wzrostem częstotliwości.

Fala wchodząca w obszar danego ośrodka wymusza na jego cząsteczkach (drgających z własną częstotliwością f0) drgania z częstotliwością f. W przypadku prostopadłego padania, cząsteczki na powierzchni badanego ośrodka wytwarzają falę płaską spójną z falą padającą jednak przesuniętą w stosunku do niej w fazie o kąt ϕ, co wyraża się wzorem:

ctg ϕ = κ f0 / ( f² - f0² ) ,

gdzie κ oznacza współczynnik tłumienia drgań.

Podobny mechanizm nałożenia się fali przychodzącej oraz fali wtórnej występuje na co raz głębszych „warstwach” cząstek, tak więc fala ciągle zmienia swoją fazę w stosunku do fazy fali pierwotnej. Stąd mówimy o prędkości przesuwania się fazy (prędkości fazowej fali). Jak wiemy każda składowa światła ma inną częstotliwość zatem i inną prędkość fazową w danym ośrodku, tak więc poruszają się one w nim z różnymi prędkościami. Stąd też ich różne współczynniki załamania w tym samym ośrodku. Zjawisko to nazywamy właśnie dyspersją.

Dyspersję materiału rozszczepiającego światło można wyznaczyć dla każdej długości fali przy pomocy wzoru:

Dn = dn / dλ ,

Gdzie λ oznacza długość fali λ_k , dla której obliczamy wartość dyspersji, która z kolei jest tangęsem kąta nachylenia krzywej dyspersji (zależność dyspersji od długości fali) dla długości fali λ_k.

2. Zasady wykonania ćwiczenia:

Rys.1. Wyznaczanie kąta łamiącego pryzmatu: a) odbicie promieni od ścian pryzmatu; b) ilustracja rozważań geometrycznych.

Na początku ćwiczenia należało wyznaczyć kąt łamiący pryzmatu oświetlając jego wierzchołek (rys 1a) i znajdując połowę różnicy, pomiędzy odczytanymi kątami odbicia wiązki od ścianek pryzmatu.

Powyższa zależność ( ϕ = (a - b) / 2 ) została otrzymana w następujący sposób (patrz rys. 1b):

a - b =360 - 2α - 2β ,

gdzie a i b położenia kątowe lunety przez którą obserwujemy światło odbite od ścianek pryzmatu;

α = 90 - ϕ1 oraz

β = 90 - ϕ2.

Stąd:

a - b = 360 -2(90 - ϕ1) - 2(90 - ϕ2) = 2ϕ1 + 2ϕ2 = 2ϕ .

Ostatecznie:

ϕ = (a - b) / 2

Następną częścią ćwiczenia było wyznaczanie współczynnika załamania światła (dla wielu długości fali) metodą najmniejszego odchylenia.

Patrząc na rys. 2a można wywnioskować następujące zależności:

ϕ = β1 + β2

ε = (α1 - β1) + (α2 - β2)

ε = α1 + α2 - ϕ

Stopniowo obracając pryzmatem i obserwując kąt wiązki załamanej przez pryzmat, wiązka osiąga pewien kąt minimalny. Przy dalszym obracaniu pryzmatem w tę samą stronę kąt załamania znów zwiększa się. Kąt minimalny osiągany jest przy symetrycznym przejściu wiązki przez pryzmat tzn. gdy:

α1 = α2 = α oraz β1 = β2 = β

Następnie możemy napisać na podstawie wcześniejszych zależności:

ε_min = 2α - ϕ skąd: α = (ε_min + ϕ) / 2 oraz:

ϕ = 2β skąd: β = ϕ / 2

Podstawiając uzyskane zależności do wzoru na współczynnik załamania otrzymujemy:

n = sin ((ε_min + ϕ) / 2) / sin (ϕ / 2)

Z tego wzoru będziemy wyznaczać współczynnik załamania, znając kąt łamiący pryzmatu ϕ oraz kąt najmniejszego odchylenia ε_min dla danej długości fali.

3. Wykonanie ćwiczenia i uzyskane wartości pomiarów:

Badając kąt łamiący pryzmatu wg wyżej objaśnionych zasad otrzymaliśmy następujące kątowe płożenia a i b lunety dla wiązek odbitych od ścianek pryzmatu oraz odpowiadające im wartości kąta łamiącego pryzmatu:

a	b	ϕ	ϕśr	Δϕ
305°28'	185°8'	60°10'	60°30'	6'
245°52'	124°40'	60°36'
		60°46'

Na błąd wyznaczania kąta łamiącego pryzmatu składa się: błąd odczytu z noniusza (2') oraz szerokość kątowa obrazu szczeliny dzielona przez 2 (4'). Więc Δϕ = 2' + 4' = 6'

Otrzymaliśmy zatem kąt łamiący pryzmatu: ϕ = 60°30' ± 6'

Następnie kąty najmniejszego odchylenia przez pryzmat dla wyraźniejszych prążków różnych barw.

Najpierw dla prążka czerwonego mierzyliśmy szerokość przedziału martwego (przedziału w którym mimo zmiany kąta ustawienia pryzmatu, zmiany położenia prążka są niewidoczne dla oka ludzkiego). Wartość ta potrzebna będzie do oszacowania błędu wyznaczania wartości minimalnych odchyleń dla danych prążków.

Następnie przeszliśmy do pomiarów minimalnych odchyleń dla poszczególnych prążków. Uzyskane wartości odchyleń oraz odpowiadające im długości fal zawarte są w tabeli:

Barwa prążka	Odczyt 1	Odczyt 2	εmin - Śr. z odczytów	Δεmin	Długość fali λ
Czerwony	280°16'	280°26'	280°21'	1°16'	640
Pomarańczowy	280°06'	280°06'	280°06'			607,4
Pomarańczowo-żółty	279°48'	280°00'	279°54'			594,5
Żółty	279°48'	279°40'	279°44'			585,2
Zielony1	279°28'	279°34'	279°31'			540
Zielony2	279°20'	279°26'	279°23'			537,5
Zielony3	279°12'	279°18'	279°15'			534,1
Niebieski1	278°54'	279°04'	278°59'			488,4
Niebieski2	278°54'	278°02'	278°58'			488,5
Fiolet	277°28'	277°34'	277°31'			471,5
Blady fiolet	277°00'	277°10'	277°05'			450
Ciemny fiolet	276°44'	276°54'	276°49'			433,4

Długość fali odczytywana była z tabeli dołączonej razem z przyrządami do wykonania ćwiczenia, na podstawie podobieństwa barwy i położenia prążka w spektrum neonu (ponieważ stanowisko nie zostało wyposażone w aparaturę do pomiarów długości fali). Dokładność tej metody pozostawiam bez komentarza. Określam więc błąd jej pomiaru na około 20 nm.

Tabela pomiarów martwego przedziału dla prążka czerwonego:

Wejście w martwy przedział - odczyt 1	Wejście w martwy przedział - odczyt 2	Średnia odczytów wejścia	Wyjście - odczyt 1	Wyjście - odczyt 2	Średnia odczytów wyjścia	Szerokość	Szerokość śr.
282°40'	282°50'	282°45'	280°02'	280°10'	280°6'	2°39'	2°21'
281°00'	281°12'	281°06'	279°00'	279°06'	279°03'	2°03'

Na błąd minimalnego odchylenia składa się: błąd odczytu (2'), szerokość kątowa obrazu szczeliny dzielona przez 2 (4'), oraz szerokość martwego przedziału dzielona na 2 (1°10'), więc błąd Δε_min = 2' + 4' + 1°10' = 1°16'.

Rachunek błędu dla wyznaczanego współczynnika n załamania światła:

Wsp. n wyraża się wzorem:

n = sin ((ε_min + ϕ) / 2) / sin (ϕ / 2) ,

więc zależy on od dwóch zmiennych: ε_min oraz ϕ i należy obliczać jego błąd metodą różniczki zupełnej.

Δn = | dn / dε_min | * Δε_min + | dn / dϕ | * Δϕ , czyli:

dn / dϕ = ( (cos ( (ϕ + ε_min ) / 2 )) / 2 * sin (ϕ / 2) - (cos (ϕ / 2)) / 2 * sin (ϕ / 2) * (sin ( (ϕ + ε_min ) / 2 )) / 2 )

/ sin²(ϕ / 2)

dn / dε_min = (cos ( (ϕ + ε_min ) / 2) ) / 2 / sin (ϕ / 2)

Po zamianie wartości pomiarowych na radiany obliczyłem wg powyższego wzoru błędy minimalnych odchyleń które umieszczam w poniższej tabeli:

Barwa prążka	Obliczony wsp. Zał. N	Obliczony błąd Δn
Czerwony	1,9531596	0,022285
Pomarańczowy	1,9539691	0,022277
Pomarańczowo-żółty	1,9546100	0,022271
Żółty	1,9551395	0,022265
Zielony1	1,9558217	0,022259
Zielony2	1,9562381	0,022254
Zielony3	1,9566518	0,022250
Niebieski1	1,9574712	0,022241
Niebieski2	1,9575221	0,022241
Fiolet	1,9617886	0,022191
Blady fiolet	1,9630027	0,022175
Ciemny fiolet	1,9637359	0,022165

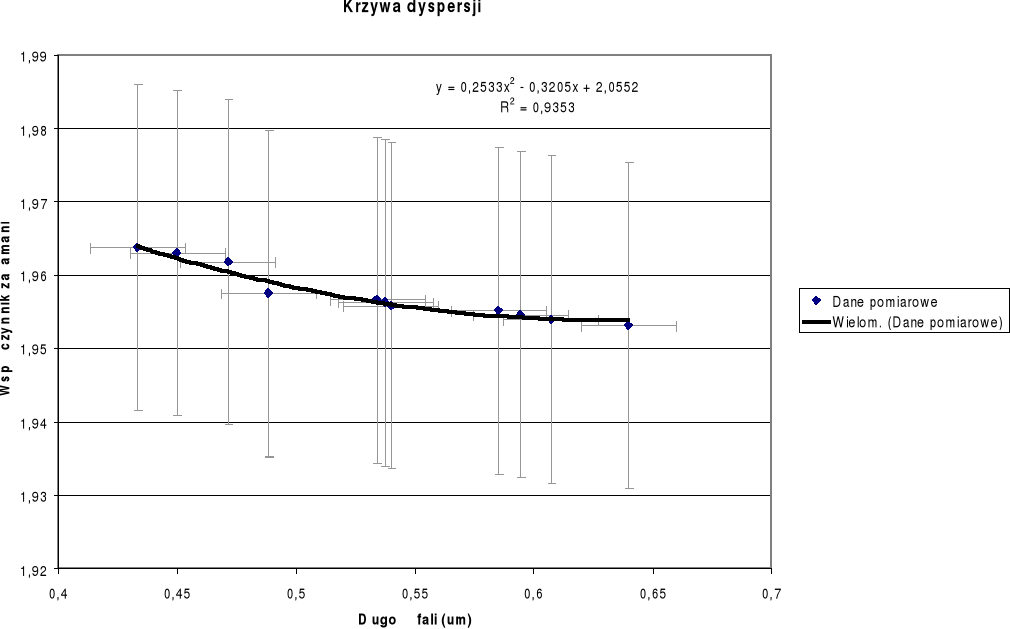
Uzyskany wykres zależności długości fali i współczynnika załamania n, wraz z kwadratami błędów można zobaczyć na dołączonym wykresie. Został on uzyskany poprzez aproksymację wielomianową punktów pomiarowych. Uzyskane równanie krzywej to:

n = 0,2533λ² - 0,3205λ + 2,0552

Dla uzyskania dostatecznie dużych współczynników równania długość fali wyrażona została w μm.

Wyznaczenie wartości dyspersji dla kilku przykładowych długości fali:

Dyspersję wyznaczę dla długości fali: 640 nm, 594,5 nm oraz 433,4 nm

Wzór na dyspersję to D = | dn / dλ | , zatem dysponując równaniem krzywej dyspersji mogę wyznaczyć jej pochodną, która wynosi:

dn / dλ = 0,2533λ - 0,3205 ,

więc podstawiając uzyskałem odpowiednio: 0,158388; 0,1699132 oraz 0,2107198.

Rachunek błędów wyznaczenia dyspersji:

Na podstawie wzoru D = | dn / dλ | widać że można zastosować metodę różniczki zupełnej.

Otrzymaliśmy odpowiednio następujące wartości błędów dyspersji:

0,006756772; 0,007652156 oraz 0,012102508.

4. Wnioski:

Uzyskana przez nas krzywa dyspersji ma kształt zgodny z teoretycznym, co potwierdza dość dobrą dokładność wykonanych pomiarów, które mieszczą się w obliczonych zakresach błędów. Można mieć spore uwagi co do prymitywnych metod odczytu długości fali w tym ćwiczeniu, jednak -jak się okazuje- nie miało to zbyt dużego wpływu na wyniki. Elementem, który nie wyszedł najlepiej, jest pomiar szerokości martwego przedziału, który wyszedł zbyt duży mimo kilkakrotnego powtórzenia pomiarów. Spowodowało to wręcz gigantyczne zakresy obliczonych błędów dla wartości ε_min oraz w konsekwencji dla uzyskanych wartości błędów współczynnika n.

1

6

Bibliografia:

1. M. Kozielski - „Fizyka dla szkół średnich t. 3” - 1996 r.

---