I. Cel ćwiczenia.

Wyznaczanie pracy wyjścia elektronów z metalu metodą prostej Richardsona.

II.Podstawy fizyczne.

Termoemisją nazywamy zjwisko wychodzenia elektronów z rozgrzanej powieszchni danego ciała do otaczającej przestrzeni. Zjawisko to jest jednym z kilku zjawisk emisji elektronów pod wpływem dostarczonej energii. W zależności od sposobu doprowadzenia tej energii rozróżnia się następujące rodzaje emisji:

-termoelektronowa: zachodzi w wyniku nagrzania danego ciała do odpowiednio wysokiej temperatury;

-fotoelektronowa: występuje wskutek pochłaniania przez substancję energii promieniowania elektromagnetycznego;

-wtórna: zachodzi wskutek bombardowania ciała elektronami lub jonami;

-polowa: zachodzi pod działaniem bardzo silnego pola elektrycznego.

III.Opis ćwiczenia.

a) Metoda wyznaczania temperatury katody.

Temperaturę katody można wyznaczyć opierając się na wzorze Richardsona-Dushmana na gęstość całkowitego prądu emisji:

(1)

gdzie A nosi nazwę stałej Richardsona i dla niektórych materiałów równa się 120
.

Elektrony aby znaleźć się poza objętością metalu muszą pokonać barierę potencjału. Można to przedstawić w postaci następującej zależności:

(2)

gdzie
-wysokość bariery potencjału w odległości x od powieszchni emitującej (katody)

-potencjał wyjścia

-hamująca różnica potencjałów

Podstawiając do wzoru (1)
otrzymamy gęstość prądu w odległości x od powieszchni emitującej z uwzględnieniem hamującego pola elektrycznego:

(3)

Wielkość
nosi nazwę potencjału elektrokinetycznego. Z doświadczenia wynika, że zależność (3) jest słuszna dla
.

Korzystając ze wzoru (3) można wyznaczyć temperaturę powieszchni emitującej. W tym celu należy wyznaczyć zależność prądu od hamującej różnicy potencjałów między powieszchnią emitującą (katodą) a określonym punktem oddalonym o x=a od tej powieszchni, w którym w naszym przypadku znajduje się anoda.

Podstawiając we wzorze (3) zamiast
wartości natężenie prądu anodowego
oraz
,
otrzymamy:

(4)

a po zlogarytmowaniu równanie prostej typu y=ax+b:

(5)

gdzie
,
,
i z której nachylenia
można wyznaczyć temperaturę T:

(6)

b) Metoda wyznaczania pracy wyjścia.

Wyznaczając z kolei natężenie prądu termoemisji
z parametru b prostej dla różnych wartości temperatury T (różnych napięć żarzenia) można korzystając ze wzoru (1) wyznaczyć pracę wyjścia
:

(7a)

(7b)

Dzieląc stronami oba równania a potem logarytmując obie strony otrzymamy wyrażenie na pracę wyjścia

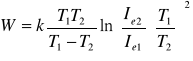
(8)

gdzie
- wartości prądu
dla
, dla różnych napięć żarzenia.

4.Wykonanie ćwiczenia.

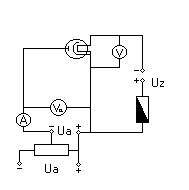
Rys. 1

Po zestawieniu układu pomiarowego jak na rys. 1 zmierzona została charakterystyka

dla napięć żarzenia 4V i 6V. Pomiary były wykonane poczynając od
aż do napięcia przy którym jeszcze nie trzeba zmieniać najczulszego (najniższego) zakresu mierzonego prądu
na mikroamperomierzu.

Otrzymane wyniki dla obu serii pomiarwych przedstawiają tabele na następnej stronie:

Uż=4V					Uż=6V
Lp.					Lp.
		A	V				A	V
1.	1	0,2	0,405		1.	1	0,2	0,851
2.	5	1	0,264		2.	5	1	0,682
3.	10	2	0,198		3.	10	2	0,61
4.	13	2,6	0,178		4.	15	3	0,566
5.	15	3	0,164		5.	20	4	0,541
6.	20	4	0,137		6.	25	5	0,518
7.	23	4,6	0,129		7.	30	6	0,5
8.	25	5	0,12		8.	35	7	0,483
9.	30	6	0,101		9.	40	8	0,469
10.	32	6,4	0,1		10.	45	9	0,457
11.	35	7	0,088		11.	50	10	0,45
12.	40	8	0,08		12.	55	11	0,44
13.	43	8,6	0,074		13.	60	12	0,431
14.	45	9	0,07		14.	65	13	0,418
15.	50	10	0,06		15.	70	14	0,413
16.	55	11	0,052		16.	75	15	0,409
17.	58	11,6	0,046		17.	80	16	0,403
18.	60	12	0,042		18.	85	17	0,394
19.	62	12,4	0,04		19.	90	18	0,388
20.	65	13	0,035		20.	95	19	0,384
21.	68	13,6	0,037		21.	100	20	0,378
22.	70	14	0,029		22.	105	21	0,372
23.	72	14,4	0,028		23.	110	22	0,367
24.	75	15	0,024		24.	115	23	0,363
25.	78	15,6	0,021		25.	120	24	0,359
26.	80	16	0,019		26.	125	25	0,356
27.	85	17	0,013		27.	130	26	0,353
28.	86	17,2	0,012		28.	135	27	0,345
29.	90	18	0,01		29.	140	28	0,342
30.	95	19	0,004		30.	145	29	0,339
					31.	150	30	0,335

Następnie korzystając ze wzoru (5) gdzie
,
,
z metody sumy najmniejszych kwadratów wyznaczam współczynnik
a następnie temperaturę T:

Wykresy zależności
oraz wyznaczenie współczynnika a dla poszczególnych napięć żarzenia zostały wykonane w programie komputerowym NKWADRAT w pracowni.

Uż=4V

Uż=6V

Współczynniki a dla odpowiednio Uż=4V i Uż=6V wyszły:

-11,38±0.08

-9,80±0.06

dla współczynnika t-Studenta t=2,0452

Mając
,
mogę obliczyć wartości temperatur
,
katody.

Błędy wartości
,
liczę metodą różniczki zupełnej:

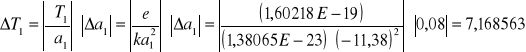
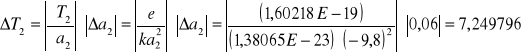
Mając wartości temperatur katody można wyliczyć za pomocą wzoru (8) pracę wyjścia W elektronów.

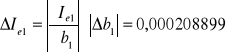
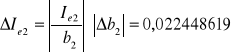
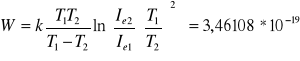
J

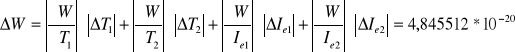
J

5.Wnioski.

Temperatury katody otrzymane przez mój zespół są obarczone niewielkim błędem względnym wynikającym z dużej dokładności pomiarów napięcia (woltomierz cyfrowy) od prądu oraz dokładnością wykonania ćwiczenia.

Metoda wyznaczania pracy wyjścia elektronów okazała się dużą niedokładnością wyników. Spowodowane jest to zmianą temperatury katody pociąga za sobą zmianę wartości A (patrz wzór (7a) i (7b) która została przyjęta za stałą przy wyprowadzeniu wzoru na pracę W (patrz wzór (8)). Wartość ta powoduje dużą wartość błędu względnego wynoszącego w naszym przypadku 14% co jest jednak błędem mieszczącym się w normie.

---