1.Reakcje typowych więzów

- geometryczne - holenomiczne
- kinematyczne - nieholenomiczne
- niestacjonarne - skleronomiczne
- gładkie - praca reakcji =0
- szorstkie - praca reakcji #0
- dwustronne - warunek nałożony w postaci równości
- jednostronne - warunek nałożony w postaci nierówności

Tutaj jeszcze przydałyby się rysuneczki, ale skoro ktoś jest dopuszczony do egzaminu to chyba umie rozrysować więzy?

2. Twierdzenie o trzech siłach. Przykład stosowania.

Jeżeli na ciało sztywne działają trzy siły o nierównoległych liniach działania, to ciało pozostaje w równowadze tylko wtedy, gdy:

• linie działania tych sił przecinają się w jednym punkcie (a)

• wielobok sił jest zamknięty, tzn. siły tworzą trójkąt sił (b)

3. Moment siły względem bieguna i względem osi.

Momentem siły względem punktu (bieguna) nazywamy wektor Mo(P)który jest prostopadły do płaszczyzny wyznaczonej przez prostą działania siły i punkt.

Wartość wektora momentu jest równa:

Odległość d jest odległością prostej działania siły od punktu i nazywana jest ramieniem siły.

Zwrot wektora momentu jest taki, aby patrząc od jego strzałki na płaszczyznę wyznaczoną przez siłę i punkt, widać było obrót siły względem punktu w kierunku przeciwnym do ruchu wskazówek zegara czyli inaczej, aby trójka wektorów zaznaczonych na rysunku była prawoskrętna.

Moment siły względem bieguna jest zerem, gdy prosta działania siły przechodzi przez ten biegun.

Momentem Siły Względem Osi nazywamy moment rzutu tej siły na płaszczyznę prostopadłą do osi względem punktu przebicia osi i płaszczyzny.

Moment Siły Względem Osi Jest Wektorem O Następujących Cechach:

1. Wartość Fπ . r.

2. Kierunek zgodny z kierunkiem osi.

3. Zwrot zgodny z regułą śruby prawoskrętnej.

Jeżeli zwrot momentu jest zgodny ze zwrotem osi to moment uważamy za dodatni, a gdy przeciwny - za ujemny.

Moment Siły Względem Osi Jest Równy Zero:

1. Fπ = 0 - Siła jest równoległa do osi l

2. r = 0 - Linia działania siły przecina oś.

Moment siły względem osi będzie równy zero wtedy, gdy siła i oś leżą w jednej płaszczyźnie λ

4. Składanie sił równoległych.

    -   wypadkowa dwóch sił równoległych o zgodnych zwrotach  jest równa sumie wartoŚci sił składowych, jest do nich równoległa, ma ten sam zwrot, a jej prosta działania przechodzi między siłami składowymi, dzieląc odcinek między nimi w stosunku odwrotnie proporcjonalnym do wartości tych sił.
    -  wypadkowa dwóch sił równoległych o przeciwnych zwrotach i różnych wartościach liczbowych,  jest równa różnicy wartości tych sił, jest do nich równoległa, ma zwrot zgodny ze zwrotem siły większej, jej prosta działania przechodzi na zewnątrz siły większej i dzieli odcinek między siłami zewnętrznymi w stosunku  odwrotnie proporcjonalnym do wartości tych sił.

5. Wykazać że moment pary sił jest niezmiennikiem.

Jest niezmiennikiem czyli nie zależy od wyboru bieguna redukcji O

“Punkt zaczepienia momentu skupionego M jest nieistotny, bo moment jako wynik dzialania pary sił jest wektorem swobodnym”

6. Redukcja dowolnego przestrzennego układu sił wektor główny W_g i moment główny M_g.

Jeżeli dowolny przestrzenny układ sił
zaczepionych w punktach
,
zredukujemy do bieguna redukcji
, dostaniemy wektor główny
, moment
, przy czym:

7. Dwa niezmienniki redukcji.

Istnieją 2 niezmienniki redukcji dowolnego przestrzennego układu sił (wielkości, które nie zależą od wyboru bieguna redukcji).

Wektor główny:

Rzut momentu głównego na kierunek wektora głównego:

8. Skrętnik - równanie osi centralnej.

Jeżeli w danym biegunie redukcji układ sił redukuje się do wektora głównego siły i wektora głównego momentu leżących na tej samej prostej to mówimy że układ redukuje się do skrętnika.

Równanie osi centralnej jest to prosta mająca te własności że dla każdego punktu tej prostej układ redukuje się do skrętnika.

λ jest dowolną wielkością skalarną tak dobraną, aby iloczyn λW miał wymiar długości.

Otrzymane równanie jest wektorowym równaniem prostej l przechodzącej przez punkt S i równoległej do wektora głównego W. Prostą tę nazywamy osią centralną układu sił lub osią skrętnika.

9. Przypadki szczególne redukcje dowolnego przestrzennego układu sił.

Redukcja sił w punkcie
S=0     M=0 układ zerowy
S#0     M=0 jeden wektor
S=0     M#0 para sił
S#0     M#0 układ złożony z 3 wektorów

Redukcja  do najprostszej postaci
S=0     M=0 układ zerowy
S#0     K=0 wypadkowa
S=0     M#0 para sił
K#0  skrętnik
K=M (skalarnie) S

Równoległy
S=0     M=0 układ zerowy
S#0     M=0 wypadkowa
S=0     M#0 para sił

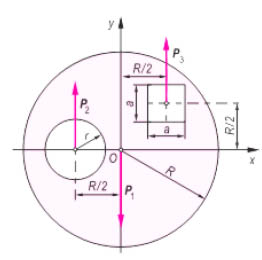
10. Środek sił równoległych - definicja, wzory na środek układu sił.

Środkiem sił równoległych nazywamy punkt O(x0, y0, z0), przez który zawsze przechodzi linia działania wypadkowej, niezależnie od obrotu tych sił o dowolny (ale ten sam dla wszystkich sił) kąt Φ wokół ich punktów zaczepienia.

Współrzędne punktów:

Gdzie:

P_i - i-ta siła z układu sił równoległych

X_i, Y_i, Z_i - współrzędne sił

11. Środek ciężkości krzywej

W najogólniejszym przypadku do wyznaczenia współrzędnych środka ciężkości krzywej używamy wzorów:

Gdzie:

X_c, Y_c, Z_c - współrzędne środka ciężkości krzywej

X, Y, Z - współrzędne siły ciężkości krzywej

- długość całkowita linii

12. Środki ciężkości figur płaskich.

Współrzędne środka ciężkości figury płaskiej wyznaczamy ze wzorów

   
              
gdzie A - pole powierzchni figury płaskiej w m².
Przy wykorzystaniu definicji momentów statycznych figur płaskich współrzędne środka ciężkości figury płaskiej obliczymy ze wzorów

  
               
gdzie S_y - moment statyczny względem osi y,  S_x - moment statyczny względem osi x.
Przydatne twierdzenia do obliczania współrzędnych środka ciężkości figury płaskiej

• gdy figura płaska ma oś symetrii, to środek ciężkości leży na tej osi,

• jeżeli figura płaska ma dwie osie symetrii, to środek ciężkości leży w punkcie przecięcia tych osi.

13. Metoda rozbicia i dopełnienia.

Metoda rozbicia polega na tym że daną figurę płaską rozbijamy myślowo na elementy proste, których współrzędne środków ciężkości są znane ( prostokąty, trójkąty itp.) następnie zaczepiamy w tych środkach ciężkości siły proporcjonalne do pól powierzchni tych elementów ( przy założeniu że figura jest jednorodna), po czym stosujemy podane wzory w wyznaczmy ( x₀, y₀ ). Pi = |Pi| - Wartosc i-tej siły xi - położenie siły. (tak samo y i z)

Metoda dopełnienia polega na tym że do figury z wycięciami czy otworami dodajemy pewne figury otrzymując w ten sposób ciało najczęściej symetrycznie, w każdym razie o znanych współrzędnych środków ciężkości. Wyznaczając siłę ciężkości w środku figury dodajemy jeszcze siły w środkach ciężkości dodanych figur z wartością odwrotna.

14. Kratownice metoda równoważenia węzłów.

Kratownice będziemy nazywać układem prętów, który zachowuje się jak ciało sztywne. Kratownice rozwiązywać będziemy przy następujących założeniach upraszczających:

• pręty są połączone przegubami (węzłami),

• siły działające na kratownicę są przyłożone w węzłach,

• ciężary własne prętów zaniedbujemy (względnie połowę ich wartości zaczepiamy w węzłach),

• tarcie w przegubach zaniedbujemy

Aby kratownica dała się rozwiązać, musi być ona statycznie wewnętrznie i zewnętrznie wyznaczalna. Warunkiem koniecznym (ale nie wystarczającym) na to, aby kratownica była statycznie wewnętrznie wyznaczalna jest spełnienie nierówności:

Gdzie:
- liczba prętów,
- liczba węzłów kratownicy.

Statyczna wyznaczalność zewnętrzna wymaga, aby liczba niewiadomych reakcji zewnętrznych nie przekraczała liczby niezależnych równań równowagi.

Metoda równoważenia węzłów:

Polega na tym, że rozpatrujemy równowagę każdego z węzłów osobno. Po myślowym odcięciu danego węzła od kratownicy otrzymamy układ sił zbieżnych w jednym punkcie i dla takiego układu możemy ułożyć dwa niezależne równania równowagi. Należy więc rozwiązywanie rozpocząć od tego węzła, w którym schodzą się dwa pręty, a potem przechodzić do następnych węzłów w takiej kolejności, aby liczba nieznanych sił schodzących się w danym węźle nie przekraczała dwóch.

(W książce Nizioła jest przykład gdyby komuś było mało :D)

15. Objaśnić na przykładzie metodę Rittera.

Metoda Rittera jest metodą analityczną i jednokrotne jej zastosowanie umożliwia wyznaczenie sił w trzech prętach kratownicy:

• nierównoległych

• nie schodzących się w jednym węźle

• takich, aby kratownica rozpadła się na dwie oddzielne części

Po myślowym przecięciu kratownicy przez trzy pręty spełniające powyższe warunki wybieramy jedną z dwóch części kratownicy. Na wybraną część kratownicy działają znane siły zewnętrzne oraz trzy nieznane wartości siły, działające wzdłuż przeciętych prętów. Dla wybranej części kratownicy możemy ułożyć trzy niezależne równania równowagi. Równania te zapiszemy w postaci trzech momentów względem tzw. biegunów Rittera. Bieguny te są to punkty, w których przecinają się kierunki działania dwóch niezależnych sił względem bieguna Rittera. Jeżeli obliczymy sumę momentów wszystkich sił względem bieguna Rittera, to otrzymamy równanie o jednej niewiadomej.

16. Obliczanie reakcji podpór belek przy obciążeniach ciągłych

Obciążenie ciągłe w obliczeniach statyki można zastąpić jedną siłą zastępczą, ta siła zastępcza jest przyłożona w środku ciężkości figury pod wykresem q(x).

17. Współczynnik tarcia, kąt tarcia, stożek tarcia.

Siła tarcia statycznego jest to reakcja styczna (styczna składowa całkowitej reakcji), przeciwstawiająca się przesunięciu ciał względem siebie.

Ogólnie zatem siłę tarcia można zdefiniować jako siłę oporu, zapobiegającą ruchowi, który by powstał gdyby tarcia nie było. Jest więc to siła bierna, która wystąpi dla zachowania równowagi stykających się ciał.

Zależność między graniczną wartością siły tarcia, a naciskiem N określają prawa tarcia, ustalone na podstawie wielu doświadczeń wykonanych przez Coulomba i Morena dla różnego rodzaju stykających się powierzchni.

• Siła tarcia jest niezależna od wielkości powierzchni stykających się ze sobą ciał i zależy jedynie od ich rodzaju,

• Wartość siły tarcia dla ciała znajdującego się w spoczynku może zmienić się od zera do granicznej wartości, proporcjonalnej do całkowitego nacisku normalnego,

• W przypadku, gdy ciało Ślizga się po pewnej powierzchni, siła tarcia jest zawsze skierowana przeciwnie do kierunku ruchu i jest mniejsza od granicznej wartości.

Na podstawie tych praw można określić zależności między siłą tarcia T, a naciskiem normalnym N.

Największa wartość siły przesuwającej, która przy danym nacisku jeszcze nie naruszy stanu względnego spoczynku, jest równa tak zwanej rozwiniętej siły tarcia statycznego Tst.max

N - jest reakcją normalną,

µ - jest tak zwanym współczynnikiem tarcia statycznego.

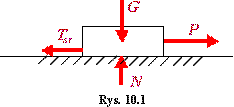
Ciała pozostają w stanie równowagi względnej, dopóki siła styczna P nie przekroczy wartoŚci rozwiniętego tarcia statycznego, to jest gdy:

Prawo tarcia statycznego jest więc nierównością, co jest rzeczą istotną.

Przy danej wartości N całkowita reakcja R może przyjmować różne wartości liczbowe i tworzyć różne kąty z normalną. Największą wartość ma całkowita reakcja Rmax przy T = Tmax (rys. 10.2).

Kąt r utworzony przez reakcję Rmax z normalną (największy z możliwych kątów wychylenia) nazywa się kątem tarcia. Tangens kąta tarcia jest współczynnikiem tarcia statycznego:

Ponieważ ciało nie może przemieszczać się w dowolnym kierunku, więc siła tarcia statycznego, mająca zwrot przeciwny do zamierzonej prędkości względnej, będzie przyjmowała różne kierunki. Maksymalna reakcja Rmax zakreśla wtedy powierzchnię stożka (w przypadku izotropowych własności ciernych - stożka kołowego), zwanego stożkiem tarcia.

Stożek tarcia - stożek obrotowy o kącie rozwarcia 2φ
Współczynnik tarcia statycznego u=tgφ
Kąt tarcia spoczynkowego φ>=0

18. Równowaga ciała na równi z tarciem S_max S_min

Siła S_max to siła maksymalna siła z jaką możemy działać na klocek, przy założeniu, że klocek pozostaje w spoczynku na równi, czyli nie „jedzie” w góre.

Siła S_min to analogicznie, minimalna siła z jaką możemy działać na klocek, przy założeniu, że klocek pozostaje w spoczynku na równi, czyli nie „jedzie” w dół.

Innymi słowy, gdy przekroczymy S_max lub będziemy działać siłą mniejszą niż S_min

to klocek zacznie się poruszać.

Gdzie:

G - ciężar klocka

T - siła tarcia

19. Tarcie cięgien- wzór Eulera

Współczynnik tarcia cięgna o walec równy jest 
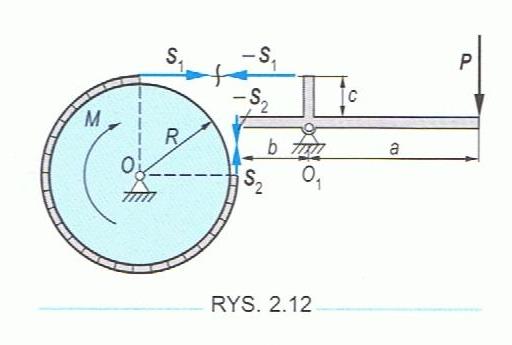
Do jednego końca cięgna przyłożona jest siła S1. W celu  zachowania równowagi sił należy znaleźć najmniejszą siłę S2, którą należy przyłożyć do drugiego końca cięgna. Rozpatrzmy w tym celu równowagę sił.

Wzór Eulera

S₂ = S₁ e^αΦ

20. Zasada działania hamulca taśmowego.

Hamulec taśmowy - hamulec, w którym elementem hamującym jest taśma owinięta na bębnie połączonym z hamowaną osią. Po naprężeniu taśmy tarcie zwiększa się na tyle, że dochodzi do zablokowania koła pasowego.

21. Zasada działania hamulca klockowego.

Para cierna jest zespołem elementów mechanicznych, przystosowanym do sztucznego wytwarzania zjawiska tarcia i siły hamowania pociągu. Najważniejsze zadanie w tym zespole spełniają dwa elementy cierne, współpracujące ze sobą na powierzchni styku ciernego, który powstaje pod działaniem siły docisku. Hamulce tego typu noszą nazwę hamulców ciernych. Podstawowymi typami hamulców ciernych są hamulce klockowe, tarczowe, i szynowe. ( do końca nie jestem upewnień)

Hamulec klockowy - hamulec, w którym elementem hamującym są klocki dociskane promieniowo do obwodu hamowanego koła.

22. Opór toczenia. Współczynnik tarcia tocznego.

Tarcie toczne (nazywane również oporem toczenia) - opór ruchu występujący przy toczeniu jednego ciała po drugim. Występuje np. pomiędzy elementami łożyska tocznego, między oponą a nawierzchnią drogi. Zwykle tarcie toczne jest znacznie mniejsze od tarcia ślizgowego występującego między ciałami stałymi, dlatego toczenie jest częstym rodzajem ruchu w technice.

μ - współczynnik tarcia tocznego

T - siła tarcia tocznego

N - siła dociskająca powierzchnie

R - promień toczącego się koła lub walca

23. Ruch punktu we współrzędnych kartezjańskich. Prędkość i przyspieszenie punktu.

Ruch punktu w układzie kartezjańskim w dowolnej chwili możemy określić za pomocą trzech równań:

Możemy go również zapisać z pomocą wektora promienia wodzącego:

Prędkość:

Wartość liczbowa:

Przyspieszenie średnie:

Przyspieszenie chwilowe:

Wartość liczbowa wektora przyspieszenia:

24. Ruch punktu w układzie naturalnym.

Często oprócz znajomości prędkości lub przyspieszenia punktu ważna jest znajomość charakteru ruchu, czy jest on przyspieszony, czy opóźniony.

Ruch jest przyspieszony, jeżeli |v(t)| jest rosnącą funkcją czasu. Ponieważ moduł funkcji jest niewygodny do badania, weźmiemy funkcję f(t)=v²(t). Jeżeli kwadrat funkcji rośnie z czasem, to i moduł funkcji rośnie. Ruch będzie przyspieszony, jeżeli df/dt>0, czyli 2va_τ >0

Jeśli va_τ >0, ruch jest przyspieszony, a jeśli va_τ <0, to jest opóźniony.

25. Krzywiznę krzywej płaskiej definiuje się jako:

gdzie
jest kątem pomiędzy stycznymi do krzywej na końcach łuku, a ΔS długością tego łuku.

Krzywizna okręgu jest w każdym punkcie jednakowa i równa odwrotności jego promienia.

Wzory na krzywiznę κ w punkcie P(x0,y0) są następujące:

Dla krzywej określonej funkcją y = f(x) w układzie kartezjańskim:

Dla krzywej określonej parametrycznie x = p(t),y = q(t) w układzie kartezjańskim:

Dla krzywej określonej funkcją w układzie biegunowym:

26. Przyspieszenie styczne i normalne w ruchu po krzywej płaskiej. Wyprowadzić wzory.

27. Kryterium ruchu przyspieszonego.

V(t) - rosnie

Ciągłe działanie siły. Przyspieszanie albo opóżnianie. ?

28. Prędkość i przyspieszenie punktu w układzie biegunowym.

W biegunowym układzie współrzędnych położenie obiektu opisujemy przez podanie

odległości obiektu od początku układu współrzędnych, czyli długości wektora wodzącego, oraz kąta, jaki tworzy wektor wodzący z poziomą osią kartezjańskiego

układu współrzędnych (osią OX).

Oznaczmy przez
wektor jednostkowy, o kierunku i zwrocie zgodnym z wektorem wodzącym obiektu. W takiej sytuacji wektor

wodzący można wyrazić jako:

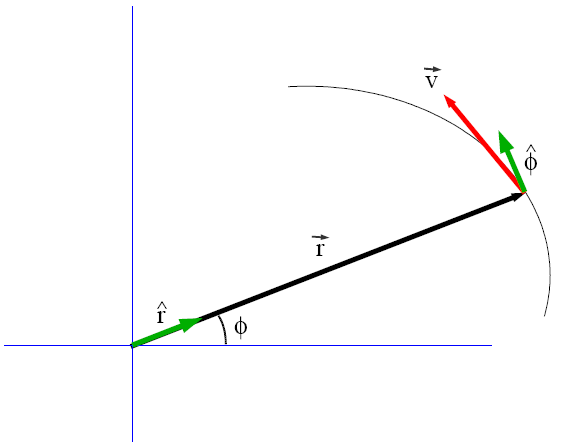
Spróbujmy policzyć wektor prędkości obliczając pochodną po czasie z wyrażenia na
:

W ten sposób wektor prędkości został wyrażony przez składową radialną vr i składową transwersalną
. Pierwsza z nich vr , odpowiada za zbliżanie się lub oddalanie obiektu od centrum układu współrzędnych, zaś druga
, odpowiada za przemieszczanie się prostopadle do wektora wodzącego (bez zmiany odległości od centrum).

Przyspieszenie, jako pochodna po czasie wektora prędkości:

Tak więc wyraziliśmy wektor przyspieszenia
przez jego składowe równoległe odpowiednio do wersora
(składowa radialna) i wersora
(składowa transwersalna). Jak widać tylko jeden z wyrazów tego równania nie zawiera pochodnej po czasie. Jest to przyspieszenie związane z przybliżaniem się lub oddalaniem obiektu bez zmiany kierunku jego wektora wodzącego, które wyraża sie przez drugą pochodna odległości po czasie.

29. Prędkość i przyspieszenie punktu w układzie cylindrycznym.

Prędkość

Przyspieszenie

30. Ruch postępowy bryły. Prędkość i przyspieszenie punktów bryły.

Ruch postępowy to ruch, w którym wszystkie punkty bryły doznają równych i równoległych przemieszczeń, gdyż wszystkie zakreślają tory o takim samym kształcie i wszystkie mają takie same prędkości. Wynika z tego, że w ruchu postępowym wszystkie punkty bryły mogą być reprezentowane przez jeden punkt - środek ciężkości, a cały ruch może być opisany tak, jak ruch punktu materialnego.

31. Ruch obrotowy bryły. Prędkość kątowa i przyspieszenie kątowe jako wektory.

Bryła w ruchu obrotowym wokół stałej osi ma jeden stopień swobody. Jako parametr określający położenie bryły w danej chwili przyjmiemy kąt obrotu
mierzony w radianach. Prędkość -
, przyspieszenie kątowe -

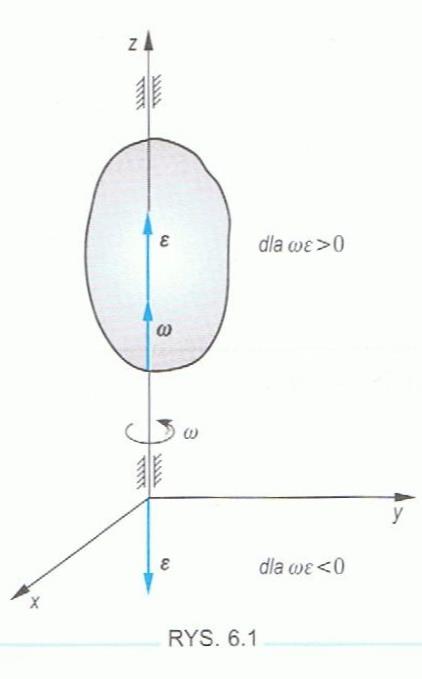
Określenie prędkości kątowej:

a)

b)
leży na osi obrotu

c) zwrot
jest zgodny z regułą prawej śruby

Określenie przyspieszenia kątowego:

a)

b)
leży w osi obrotu

c) zwrot
jest zgodny ze zwrotem
, gdy
(ruch przyspieszony), zwrot
jest przeciwny do zwrotu
gdy
(ruch opóźniony)

32. Rozkład prędkości i przyspieszeń punktów bryły w ruchu obrotowym

33. Ruch płaski

Ruchem płaskim nazywamy ruch, podczas którego wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzna kierująca.

Punkty ciała leżące na prostej prostopadłej do płaszczyzny kierującej poruszają się po takich samych torach, maja jednakowe prędkości i przyspieszenia. Zatem dla badania ruchu płaskiego wystarczy wziąć pod uwagę dowolny przekrój ciała płaszczyzna równoległa do kierującej.

- 3 punkty nieruchome; 0 stopni swobody; bryłę jednoznacznie opisują 2 punkty
     V(t) = Va(t) + ω(t) x ρ(t)

34. Przyspieszenie punktów bryły w ruchu płaskim.

(moim zdaniem mało można zrozumieć z tego objaśnienia tego pytania, ale niestety nic lepszego nie znalazłem w tych materiałach które posiadam)

35. Chwilowy środek przyspieszeń

Jest to punkt ciała, którego przyspieszenie jest równe zeru. Współrzędne chwilowe środka przyspieszeń w układzie stałym możemy otrzymać, wstawiając do wzorów na współrzędne przyspieszenia w układzie stałym:
i

36. Precesja regularna. Prędkość i przyspieszenie punktów. Objaśnić na przykładzie stożka toczącego się po płaszczyźnie. (to jest takie chujowe… nie jest na płaszczyźnie tylko stożek na stożku i żal mi się ale nigdzie nie znalazłem przykładu z płaszczyzną )

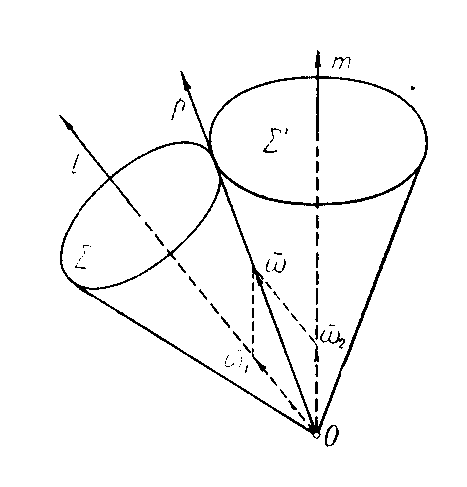
Jeżeli ciało porusza się w ten sposób, że ruch chwilowy jest w każdej chwili złożeniem dwóch obrotów równoczesnych wokół dwóch przecinających się osi, z których pierwsza l jest unieruchomiona w przestrzeni, druga zaś m ma stałe położenie w ciele, przy czym prędkości kątowe ω₁ i ω₂ tych obrotów są stałe co do wielkości, to ruch ciał nazywamy percesją regularną.

Ponieważ osie m i l się przecinają więc ruch chwilowy ciała jest obrotem z prędkością kątową ω = ω₁+ ω₂ wokół osi p przechodzącej przez punkt przecięcia osi l i m. Zauważmy że ruch chwilowy osi m jest obrotem chwilowym wokół osi l z prędkością kątową ω₁. Zatem oś m obraca się wokół osi l ze stałą prędkością ω₁. Punkt O przecięcia przecięcia się osi jest więc nieruchomy i kąt między osiami l i m jest stały. Wynika stąd że wektor ω, a więc i oś p obrotu chwilowego, tworzy stałe kąty z osiami l i m.

Oś p zakreśla w przestrzeni stożek obrotowy ∑. Ślad osi p w ciele jest również stożkiem obrotowym ∑'.

Zostawiam resztę może się komuś przyda.

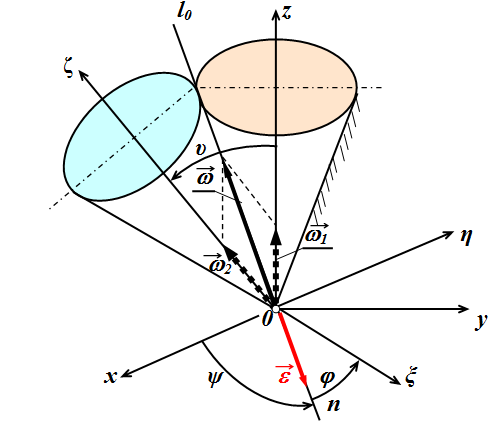
Kąt precesji
= const, stąd

oraz ω1 = const, ω2 = const

Na podstawie wzoru (77) przyśpieszenie kątowe:

Biorąc pod uwagę, że
otrzymamy

gdyż

Wektor przyśpieszenia kątowego ε o przyjętym początku w środku ruchu kulistego 0 jest prostopadły do wektorów

ω₁ i ω₂, a więc jest skierowany wzdłuż linii węzłów 0n

Przyśpieszenie liniowe a jest równe sumie geometrycznej przyśpieszenia precesyjnego a₁

i przyśpieszenia doosiowego a₂

37. Zasada różniczkowania po czasie wektora z układu ruchomego względem układu stałego

38. Prędkość bezwzględna w ruchu złożonym punktu.

Punkt porusza się ruchem złożonym, jeżeli przemieszcza się względem układu
, a układ ten porusza się względem układu stałego
(rys.)

Ruch bezwzględny punktu A, opisany za pomocą wektora promienia wodzącego.

Prędkość punktu A jest równa pochodnej wektora
względem czasu.

Czyli:

Układ

porusza się z prędkością kątową
, więc:

,
,

Prędkość bezwzględna jest więc równa:

prędkość unoszenia

prędkość względna

39. Przyspieszenie bezwzględne w ruchu złożonym punktu.

Przyspieszenie bezwzględne p równe jest pochodnej względem czasu prędkości bezwzględnej v punktu A. Ponieważ przyspieszenie to wyznaczamy w stosunku do układu nieruchomego, pochodna ta jest pochodną bezwzględną. Mamy więc:

---