Dr Aleksander Klosow

PWSZ Legnica, 2003

www.strony.wp.pl/wp/klosov/

Algorytmy i Struktury Danych

Wykład 5

SORTOWANIE SZYBKIE

POWTÓRZENIE

Sortowaniem nazywamy proces ustawiania zbioru obiektów

w określonym porządku.

Sortowanie proste, O(n^2)	Sortowanie szybkie, O(nlog(n))
Proste wybieranie Proste wstawianie Prosta zamiana	Metoda Shell'a (malejących przyrostów) Kopcowanie Quicksort (sortowanie przez podział)

Zadanie samodzielne:

Policzyć złożoność teoretyczną dla wypadku pesymistycznego trzech metod prostego sortowania dla 5 liczb całkowitych. Którą metodę należy wybrać?

SORTOWANIE

SZYBKIE

SORTOWANIE metodą malejących przyrostów

Sortowanie Shell'a

Zmodyfikowana metoda prostego wstawiania

H1=5

s=1...5

H2=3

s=1...3

H3=1

1. Ustalić ciąg malejących przyrostów H₁, H₂,... H_t;

2. Zastosować metodę prostego wstawiania do sortowania co H_i elementu

3. Zmniejszyć przyrost (i:=i+1). Powtórzyć krok 2.

SORTOWANIE metodą malejących przyrostów

Realizacja Pascal

procedure sortowanieShella; const t=4; var i,j,k,s: integer; x:integer; m:1..t; h:array[1..t] of integer; begin h[1]:=9; h[2]:=5; h[3]:=3; h[4]:=1; {przyrosty} for m:=1 to t do begin k:=h[m]; s:=-k; {wartownik} for i:=k+1 to n do begin x:=a[i]; j:=i-k; if s=0 then s:=-k; s:=s+1; a[s]:=x; while x<a[j] do begin a[j+k]:=a[j]; j:=j-k; end; a[j+k]:=x; end end end

SORTOWANIE metodą malejących przyrostów

Analiza złożoności

Najlepsze przyrosty wg Knuth D.E., The Art. Of Computer Programming

1, 4, 13, 40, 121, ... , H_k-1= 3H_k+1, t = [log₃n]-1

1, 3, 7, 15, 31, ... , H_k-1= 2H_k+1, t = [log₂n]-1

Złożoność teoretyczna: O(n^1.2)

SORTOWANIE metodą podziału O(n log n)

Sortowanie Quicksort (Strategia: Dziel i zwyciężaj)

L Oś P

i m j

A[i] <=Oś A[j]>Oś

Krok 1. Dziel

Tablica A[L..P] jest dzielona, drogą zamiany miejscami jej elementów, na dwie niepuste podtablice A[L..m] oraz A[m+1..P] takie, że każdy element pierwszej podtablicy jest nie większy niż każdy elementu drugiej. Indeks m jest obliczany według reguły dzielącej (najczęściej m = (L+P) div 2).

Krok 2. Zwyciężaj

Dwie podtablice A[L..m] oraz A[m+1..P] są sortowane za pomocą rekurencyjnych wywołań algorytmu opisanego w kroku 1.

SORTOWANIE metodą podziału

Realizacja Pascal

procedure qsort(L,P:integer); var i,j,x,tmp:integer; begin i:=L; j:=P; x:=tab[(L+P) div 2]; // wyznaczenie osi podziału repeat while tab[i]<x do i:=i+1; while x<tab[j] do j:=j-1; if i<=j then begin tmp:=tab[i]; tab[i]:=tab[j]; tab[j]:=tmp; //zamiana i:=i+1; j:=j-1; end until i>j; if L<j then qsort(L,j); if i<P then qsort(i,P); end;

tab:array[1..n] of integer; begin qsort(1,n); end.

SORTOWANIE metodą podziału

Realizacja C

void sort(int L, int P) { int i = L, j = P; int m = t[div(L+P,2).quot]; do { while(t[i]<m) i++; while(m<t[j]) j--; if(i<=j) { int w=t[i]; t[i]=t[j]; t[j]=w; i++;j--; } }while(i<=j); if(L<j) sort(L,j); if(i<P) sort(i,P); }

#define N 20 int t[N]; void main() { sort(0,N-1); }

SORTOWANIE metodą podziału

Analiza złożoności

	PO	PR	T(n)	O()
Najlepszy	n⋅log(n)	(n/6)⋅log(n)	(7/6)⋅n⋅log(n)	O(n⋅log(n))
	-	-	Tmin⋅2⋅ln(2)	O(n⋅log(n))
Najgorszy	-	-	-	O(n^2)

Słabości metody: 1) Powolna dla małych n;

2) Wymaga dużo pamięci operacyjnej.

Najlepszy przypadek: kiedy oś podziału jest medianą.

MEDIANA

Medianą n obiektów nazywa się obiekt mniejszy (≤) od połowy n obiektów oraz większy (≥) od drugiej połowy n obiektów.

1

1

1

1

2

3

3

4

4

12

5

16

8

0

10

7

3

11

Metody znajdowania mediany:

- znajdowanie (n/2)-tego najmniejszego elementu ciągu

- algorytm Hoare'a oparty na metodzie podziału z sortowania szybkiego

SORTOWANIE przez kopcowanie O(n log n)

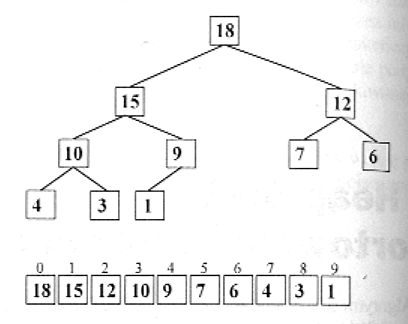
Pojęćie kopca Kopcem, lub stertą, nazywamy drzewo binarne, w którym każda wartość w węźle poniżej danego jest od niego mniejsza. Zasady reprezentacji kopca w postaci tablicy jednowymiarowej: 1/ Wierzchołek kopca umieść w T[0] 2/ Dla dowolnego węzła w T[i] jego lewy syn to T[2i+1], a prawy syn to T[2i+2].

ALGORYTM sortowania przez kopcowanie

1/ Ułuż dane w kopiec

2/ Usuń wierzchołek z kopca poprzez zamianę go z ostatnim liściem

3/ Przywróć własność kopca dla pozostałej części kopca

4/ Idź do kroku 2

Krok 3:

3.1/ Jeśli wierzchołek jest większy od obojga dzieci, wyjdź

3.2/ Zamień wierzchołek z większym dzieckiem

3.3/ Przywróć własność kopca w tej części kopca, w której nastąpiła zamiana

Krok 1:

1.1/ Ustaw licznik i = n/2 (ostatni węzeł przed liśćmi)

1.2/ Wybierz element T[i]

1.3/ Wykonaj kroki 3.1, 3.2, 3.3

1.4/ Dopuki i> 0 wykonaj i=i-1

REALIZACJA w języku C kopcowania

void heapsort(int T[], int n) { int k, tmp; for(k=n/2; k>0; k--) przywroc(T,k,n); do { tmp = T[0]; T[0] = T[n-1]; T[n-1] = tmp; n--; przywroc(T,1,n); } while (n>1); }

// program główny #define rozmiar 14 void main() { int i, T[rozmiar] = {}; for(i=0;i<rozmiar;i++) cout << T[i] << " "; cout << endl; heapsort(T, rozmiar); for(i=0;i<rozmiar;i++) cout << T[i] << " "; }

REALIZACJA w języku C funkcji przywracania kopca

void przywroc(int T[], int k, int n)

{ int i,j;

i = T[k-1];

while(k <= n/2)

{

j=2*k;

if( (j<n) && (T[j-1]<T[j]) ) j++;

if(i >= T[j-1]) break; // wyjście z pętli while

else

{

T[k-1] = T[j-1];

K=j;

}

}

T[k-1] = i;

}

SORTOWANIE przez zliczanie

Zaleta:

- Liniowy czas działania, O(n)

Założenie:

- Każdy z elementów sortowanych jest liczbą całkowitą z przedziału 1..k

Koncepcja:

1. Wyznaczenie dla każdej liczby wejściowej x ile elementów jest mniejszych od x.

2. Umieszczenie x na pozycji, którą wyznacza liczba z kroku 1.

Cecha metody:

• brak operacji porównywania!

• Potrzebuje dwóch tablic pomocniczych.

SORTOWANIE przez zliczanie

Opis algorytmu

Dano:

A[1..n] - tablica elementów do posortowania

k - górna granica wartości elementów z A

C[1..k] - tablica pomocnicza

B[1..n] - tablica posortowana

1 krok. (n = 7, k = 5) 1 2 3 4 5

A

3

2

4

5

1

2

4

→

C

1

2

1

2

1

2 krok. 1 2 3 4 5

A

3

2

4

5

1

2

4

→

C

1

3

4

6

7

3 krok. 1 2 3 4 5

B

4

→

C

1

3

4

5

7

SORTOWANIE przez zliczanie

Realizacja, Pascal

procedure countingsort(A:array[1..n] of integer; k:integer; var B:array[1..n] of integer) var i,j:integer; C: array[1..k] of integer; B: array[1..n] of integer; Begin for i:=1 to k do C[i]:=0; for i:=1 to n do C[A[i]]:=C[A[i]]+1; {krok 1} for i:=2 to k do C[i]:=C[i]+C[i-1]; {krok 2} for i:=n downto 1 do {krok 3} begin B[C[A[i]]]:=A[i]; C[A[i]]:=C[A[i]]-1; end; End;

---