Podstawy fizyczne

Ze względu na zachowanie magnetyczne materiały dzielimy na diamagnetyki, paramagnetyki, ferromagnetyki, anty-ferromagnetyki. Jest to podział najbardziej podstawowy.

W przypadku diamagnetyka ruch elektronu po orbicie znajdującej się w polu magnetycznym powoduje wystąpienie precesji. Orbita elektronu ulega precesji wokół kierunku wektora indukcji magnetycznej
. Działający na orbitę moment siły, który wymusza ustawienie się orbitalnego momentu magnetycznego wzdłuż kierunku pola, a orbitalnego momentu pędu elektronu w kierunku przeciwnym. Można udowodnić, że płaszczyzna orbity elektronu ulega precesji z tzw. częstością Larmora opisaną wzorem:

Częstość ta jest jednakowa dla wszystkich elektronów znajdujących się w danej materii (poddanej jednorodnemu polu magnetycznemu). Precesja ta (zwana precesją Larmora) powoduje wyindukowanie się skierowanego przeciwnie do pola, momentu magnetycznego atomu, w efekcie czego następuje osłabienie pola zewnętrznego. Trzeba jeszcze jednak wyjaśnić dlaczego w diamagnetykach występuje zerowy (wypadkowy) moment magnetyczny. Dzieje się tak dlatego, że momenty magnetyczny, choć niezerowe w przypadku poszczególnych cząstek, wzajemnie się znoszą. Właściwość taką mają substancje złożone z atomów, jonów, lub cząsteczek mających całkowicie zapełnione powłoki elektronowe. Do dielektryków zaliczamy m. in. Gazy szlachetne, wodór, azot, NaCl.

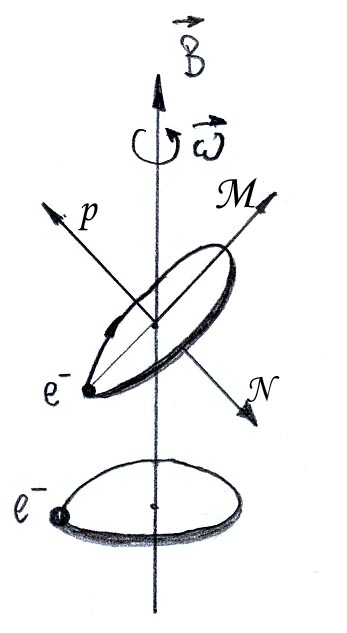
W przypadku paramagnetyków ich wypadkowy moment magnetyczny nie jest równy zero. Główną tego przyczyną jest występowanie zarówno orbitalnego ruchu elektronu jak i spinowych momentów magnetycznych. W paramagnetykach (tak jak i w dielektrykach) występuje precesja Larmora. Jednak w przypadku paramagnetyków niezerowe momenty magnetyczne pod wpływem precesji Larmora ustawiają się zgodnie z kierunkiem pola. W efekcie powstałe pole jest dużo silniejsze od przeciwnego pola (wyindukowanego na skutek precesji). Na wzrost uporządkowania momentów magnetycznych wpływają także zderzenia atomów (cząsteczek).

p- orbitalny moment magnetyczny

M- moment siły

N- orbitalny moment pędu elektronu

Do opisu właściwości magnetycznych substancji wprowadza się bezwymiarową wielkość zwaną względną podatnością magnetyczną oznaczaną przez
. Zgodnie z prawem Curie-Weissa (obowiązującym tylko dla paramagnetyków T> T_c) istnieje ścisła zależność między podatnością magnetyczną, a temperaturą:

gdzie C- stała Curie, T_c - temperatura.

Prawo to bardzo dobrze obrazuje zależność podatności magnetycznej od temperatury tylko dla dużych temperatur (to znaczy dużo większych od temperatury Curie). Dla temperatur zbliżonych do temperatury Curie krzywa teoretyczna zawsze rozbiega się z danymi doświadczalnymi.

Jeśli chodzi o ferromagnetyki to sytuacja jest w nich nieco inna niż w paramagnetykach i dielektrykach. Wewnątrz bowiem występują pewne niewielkie obszary (wielkości 1-10
m) w których występuję spontaniczne uporządkowanie momentów magnetycznych. Całkowity moment magnetyczny próbki ferromagnetyka jest sumą wektorów momentów magnetycznych poszczególnych domen. Namagnesowanie ferromagnetyka J zależy od natężenia pola H w sposób złożony. Zazwyczaj już dla niewielkich natężeń pola magnetycznego namagnesowanie osiąga stan nasycenia, co widać na poniższym wykresie.

Zależność pomiędzy natężeniem pola, namagnesowaniem, a indukcją magnetyczną opisuje wzór.

Po osiągnięciu stanu nasycenia (J=const.) zatem indukcja magnetyczna rośnie liniowo.

Zależność indukcji magnetycznej przebiega w taki sposób jedynie w przypadku gdy próbka nie była namagnesowana wcześniej (dlatego właśnie wszelkie doświadczenia zależą od historii danej próbki ferromagnetyka). Gdy zaczniemy bowiem zmniejszać natężenie pola magnetycznego indukcja pola magnetycznego zacznie maleć w zupełnie inny sposób i tak dla zerowego zewnętrznego pola, próbka nadal pozostanie namagnesowana. Krzywą pokazującą zależność indukcji B od natężenia H nazywamy krzywą (pętlą) histerezy. Gdy maksymalne natężenie jest takie, że namagnesowanie osiągnie nasycenie to mówimy o maksymalnej pętli histerezy. Gdy namagnesowanie nie osiągnęło nasycenia mówimy o cyklu cząstkowym.

Kolejną ważną wielkością fizyczną z punku widzenia magnetyzmu jest przenikalność magnetyczna (ma ona ścisły związek z podatnością magnetyczną) oznaczana literą
.

Przenikalność magnetyczna jest funkcją natężenia pola. I tak najpierw rośnie do pewnej wartości po czym maleje. Maksimum przenikalności magnetycznej przypada dla natężenia nieco mniejszego od natężenie, przy którym występuje nasycenie.

Bardzo ważna dla ferromagnetyków jest tzw. temperatura Curie. Po przekroczeniu temperatury Curie ferromagnetyk traci swoje właściwości ferromagnetyczne. Domeny rozpadają się, a momenty magnetyczne nie wykazują uporządkowania

Kolejnym ciekawym przykładem mogą być antyferromagnetyki. Zaliczamy do nich m.in. chrom, mangan. W ich wnętrzu momenty magnetyczne ustawiają się wzajemnie antyrównolegle.W wyniku tego mają one skrajnie małą podatność magnetyczną i zachowują się jak słabe paramagnetyki. Dla antyferromagnetyków istnieje charakterystyczna temperatura zwana antyferromagnetycznym punktem Curie lub punktem Neela. Niektóre antyferromagnetyki takie jak dysproz, erb mają dwie takie temperatury. Poniżej dolnej temperatury wykazują właściwości ferromagnetyczne a powyżej górnej paramagnetyczne. Własności antyferromagnetyczne posiadają jedynie w granicach tych dwóch temperatur.

W przeprowadzonym doświadczeniu do wytworzenia pola magnetycznego wykorzystuje się pole magnetyczne wewnątrz cewki. Ponieważ istnieje pewna zależność między parametrami opisującymi pole a napięciem na cewce możemy mierzyć jedynie napięcie aby określić parametry pola magnetycznego. Jak już pisaliśmy powyżej zależność natężenia, namagnesowania oraz indukcji przedstawia wzór:

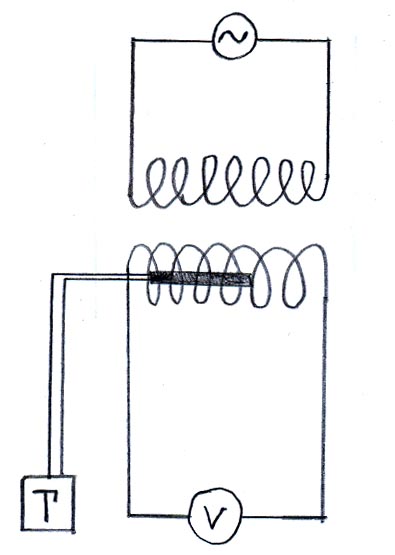
Ponieważ przez cewkę pierwotną płynie prąd zmienny, zatem wytwarza ona zmienne pole magnetyczne. Cewka wtórna znajduje się zatem w zmiennym polu magnetycznym.

W cewce wtórnej wytwarzany jest prąd indukcyjny. Zgodnie z prawem Faradaya wytworzoną SEM opisuje zależność:

Ponieważ w cewce jest Z zwojów, zatem SEM będzie Z razy większa.

Jednocześnie strumień pola magnetycznego przez powierzchnię S jest równy:
. Ponieważ wektory
i
są prostopadłe (cosinus kąta jest równy 1) możemy zapisać

Stąd :

Opis pomiaru i analiza wyników

Sterowanie pomiarem i akwizycja danych dokonane zostały za pomocą zestawionego układu komputera z odpowiednim oprogramowaniem oraz peryferiów. Pomiarów dokonano w dwóch seriach, jednej podczas ogrzewania materiału, drugiej podczas jego ochładzania. Braki w oprogramowaniu spowodowały jednak, że po zakończeniu pomiaru dysponowaliśmy tylko serią późniejszą tzn. pomiarem wykonanym podczas ochładzania ferromagnetyka. Tym samym dalsza część sprawozdania odnosi się wyłącznie do owej serii.

Pomiaru dokonano podczas ochładzania próbki od temperatury 220 st. C do 100 st. C. Ponieważ jednak do temperatury 170 st. nie zachodziły praktycznie żadne zmiany w napięciu cewki wtórnej, jak widać na wykresie 1, interesujący nas zakres temperatury (tzn. taki, w którym zachodziły zmiany w napięciu na uzwojeniu wtórnym) wynosi od 170 st. C do 100 st. C. Zakres ten przedstawiony jest na wykresie 2.

Za niepewność systematyczną pomiaru temperatury przyjęto 3% wartości zmierzonej, zaś za niepewność systematyczną pomiaru napięcia - 1,5% wartości zmierzonej plus „pięć ostatnich cyfr zakresu”, co w praktyce oznacza 0,005 V (miernik był ustalony na zakres 2V z dokładnością do 0,001 V).

Przyjmując temperaturę Curie za punkt przegięcia wykresu i tym samym punkt najostrzejszej zmiany napięcia, widać z wykresu 2, że dla badanej próbki temperatura Curie wynosi około 137 st. C.

Na podstawie pomiarów i po przyjęciu temperatury Curie w okolicach 137 st. dokonano dopasowania prostej do pomiarów metodą regresji liniowej.(wykres nr 3):

W efekcie otrzymano stąłą Curie

Na wykresie drugim zaznaczono na tej podstawie krzywą teoretyczną.

Uwaga : Krzywą teoretyczną poprowadzono także w obszarze temperatur, w których nie obowiązuje prawo Curie-Weissa. Miało to na celu obrazowe pokazanie tego iż nie można stosować tego prawa dla ferromagnetyków.

Wnioski końcowe

Niedokładności pomiarów a tym samym ich rozbieżność z krzywymi teoretycznymi wynikają przede wszystkim z nierównomiernego ogrzania próbki ferromagnetyka. Pomiaru temperatury dokonywano jedynie na jednym z końców próbki podczas gdy przeciwległy koniec mógł mieć nieco inną temperaturę. Z powodu braku czasu wyniki odczytywano w niewielkich odstępach czasu co uniemożliwiało pełne wyrównanie się temperatur.

Koleją przyczyną niedokładności była stała wartość zakresu miernika wprowadzająca coraz większe (dla coraz mniejszych napięć) niepewności systematyczne względne do wyników pomiarów.

Również pewne niedokładności wynikały z zastosowania przybliżeń, w których zakładamy, że J >>H.

T (C)	U (V)	dT	dV	dV/V
219	0,018	6,57	0,005	0,293
214	0,017	6,42	0,005	0,309
199	0,018	5,97	0,005	0,293
194	0,018	5,82	0,005	0,293
189	0,018	5,67	0,005	0,293
184	0,018	5,52	0,005	0,293
180	0,018	5,40	0,005	0,293
175	0,019	5,25	0,005	0,278
170	0,022	5,10	0,005	0,242
165	0,024	4,95	0,005	0,223
160	0,030	4,80	0,005	0,182
155	0,040	4,65	0,006	0,140
150	0,060	4,50	0,006	0,098
149	0,064	4,47	0,006	0,093
148	0,068	4,44	0,006	0,089
147	0,075	4,41	0,006	0,082
146	0,083	4,38	0,006	0,075
145	0,088	4,35	0,006	0,072
144	0,097	4,32	0,006	0,067
143	0,111	4,29	0,007	0,060
142	0,118	4,26	0,007	0,057
141	0,123	4,23	0,007	0,056
140	0,147	4,20	0,007	0,049
139	0,157	4,17	0,007	0,047
138	0,172	4,14	0,008	0,044
137	0,186	4,11	0,008	0,042
136	0,206	4,08	0,008	0,039
135	0,222	4,05	0,008	0,038
134	0,244	4,02	0,009	0,035
133	0,255	3,99	0,009	0,035
132	0,269	3,96	0,009	0,034
131	0,281	3,93	0,009	0,033
130	0,298	3,90	0,009	0,032
129	0,311	3,87	0,010	0,031
128	0,317	3,84	0,010	0,031
127	0,325	3,81	0,010	0,030
126	0,333	3,78	0,010	0,030
125	0,338	3,75	0,010	0,030
124	0,344	3,72	0,010	0,030
123	0,349	3,69	0,010	0,029
122	0,352	3,66	0,010	0,029
121	0,355	3,63	0,010	0,029
120	0,359	3,60	0,010	0,029
119	0,361	3,57	0,010	0,029
118	0,363	3,54	0,010	0,029
117	0,365	3,51	0,010	0,029
116	0,367	3,48	0,011	0,029
115	0,368	3,45	0,011	0,029
110	0,372	3,30	0,011	0,028
105	0,373	3,15	0,011	0,028
100	0,373	3,00	0,011	0,028

---