1.Redukujemy siły i momenty nma odpowiednie osie i płaszczyzny: M ma Mgx, Mgy, Mgz. Gdy mamy w przekroju N, T, Mgx, Mgz to mamy do czynienia z prostym stane obciążenia a zatem z prostym zagadnieniem wytrzymałości pręta.

2. Statycznie wyznaczalne - liczba stopni swobody równa zero, liczba równań równowagi równa liczbie niewiadomych reakcji.

Statycznie niewyznaczalne - liczba stopni swobody mniejsza od zera. Liczba n niewiadomych sił jest większa od liczby r równań równowagi. Mówimy o układzie n-r statycznie niewyznaczalnym. Konstrukcja jest przesztywniona.

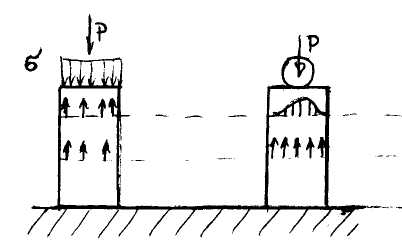
3. Zasada de Saint-Venanta: Jeżeli na pewien niewielki obszar ciała sprężystego w równowadze działają kolejno rozmaicie rozmieszczone, ale statycznie równowarte obciążenia, to w odległości od obszaru dużo większej niż jego wymiary powstają praktycznie jednakowe stany naprężenia i odkształcenia.

4. Rozciąganiem lub ściskaniem nazywamy przypadek gdy działa tylko siła osiowa P. Gdy działa zgodnie z normalną zewnętrzną przekroju to jest rozciąganie, w przeciwnym przypadku ściskanie. Prawo Hooke'a: Odkształcenie [epsilon] jst równe naprężeniom normalnym [sigma] podzielonym przez moduł Younga E.

5. Statyczna próba rozciągania - rozciąga się specjalnie przygotowaną próbkę.

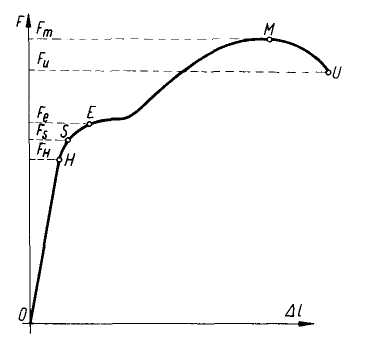
Re-granica plastyczności, Rm - wytrz. mat. na rozciąganie

Ru - naprężenie rozrywające.

Przy próbie ściskania próbka musi być o dużo większej średnicy żeby uniknąć wyboczenia.

Próba udarności - Podparta w sposób swobodny próbka zostaje w środkowym przekroju obciążona udarowo poruszającym się z określoną prędkością ciężkim wahad­łem młota (rys. 2.17). Uderzenie następuje po stronie przeciwległej karbowi. Urządzenie badawcze, w którym realizuje się tę próbę, zwane młotem udarnościowym (Charpy'ego) umożliwia wyznaczenie pracy K (J) potrzebnej do złama­nia próbki. Iloraz tej pracy przez pole S_o (cm²) osłabionego karbem przekroju próbki zwie się udarnością i oznacza symbolem KC = K/S_o (J/cm²).

6. Obliczenia wytrzymałościowe prętów na rozciąganie(ściskanie).

δ = F/A ≤ k; k = R/n; ε = ∆l / l; δ = ε E; δ = E α ∆t

∆l = N l / EA ; ∆l = α ∆t l

7. Koncentracja naprężeń. Spiętrzenie naprężeń - naprężeń przypadku zmiennych geometrii (przekrojów) przy rozciaganiu (ściskaniu) mogą wystąpić odchylenia od równomiernego rozkładu naprężeń normalnych.

8. Odkształcenia w pręcie wywołane zmianą temp.:

∆l = α ∆t l

[alfa] - wsp. Rozszerzalności liniowej;

9. Moment bezwładności przekroju.

Wykorzystamy definicję momentu bezwładności. Najpierw obliczamy moment Ix = całka po A z y² dA , przenosimy za pomocą Tw. Steinera Ix = Ixc + md²

10. Omówić sposób określania sił wewnętrznych w prętach

Wektor sił wewn. P_w = T + N, N - składowa sił w kierunku prostopadłym do przekroju; T - skł. Sił w kierunku stycznym. Gdy ustąpiła tylko jedna ze składowych mamy do czynienia z prostym zagadnieniem wytrzymałości.

11. Skręcanie, wyznaczenie kąta skręcania.

Całkowity kąt skręcenia wału jest proporcjonalny do momentu skręcającego i długości pręta, a odwrotnie proporcjonalny do modułu sprężystości postaciowej i biegunowego momentu bezwładności przekroju.

Iloczyn GJ0 występujący w mianowniku wzoru 67 nazywamy sztywnością przy skręcaniu. Im większy jest ten iloczyn, tym mniejsze jest odkształcenie, czyli pręt jest bardziej sztywny.

12. Wyznaczanie naprężeń przy skręcaniu.

Przy skręcaniu występują naprężenia styczne.

τ = Ms / Wo W0­ = Is/ρ

ρ - odległość włókien skręcanych

13. Warunek wytrzymałościowy i sztywnościowy.

Z warunku wytrzymałości wynika, że największe naprężenie styczne nie może przekroczyć naprężenia dopuszczalnego, tzn.

Warunek sztywności wału skręcanego.

Warunek ten sprowadza się do tego, że kąt skręcenia wału musi być mniejszy od dopuszczalnego.

Jest to najmniejszy moment bezwładności (biegunowy) przekroju wału, przy którym kąt skręcenia nie przekroczy wartości dopuszczalnej

14. Zginanie czyste. Założenia: nie ma M_s, jest N-siła normalna, T - siła poprzeczna (tnąca), Mg - moment gnący

Def. - jest sumą geometryczną momentów wszystkich sił prostopadłych działających na część belki, znajdującą się po jednej stronie rozpatrywanego względem środka ciężkości przekroju.

Zginanie - jest to sytuacja, kiedy dociążamy belkę momentami swobodnymi bądź momentami od sił działającymi w pł. Prostopadłej do osi belki (w pł. Przekroju belki).

15. Wyprowadzenie wzoru na naprężenia.

Założenia: hipoteza płaskich przekrojów - przy zginaniu przekroju płaskie i prostopadłe do osi belki pozostają płaskie i prostopadłe po zadziałaniu momentu zginającego.

ε = δ /E - zakładamy zginanie sprężyste.

δ = E/ ρ [ro]; - E/ δ

- E/ ρ [całka po A] y dA = 0

- E/ ρ [całka po A] yz dA = 0

- E/ ρ [całka po A] y² dA = Mg; krzywizna: -1/ ρ = δ/Ey

-1/ ρ = -Mg / E Iż

δ = Mg y / Iz -naprężenie przy zginaniu jest liniową funkcją odległości od osi obojętnej.

16. Zginanie poprzeczne. Do obliczeń elementów konstrukcyjnych (nitów, sworzni itp.) naprężenia styczne odgrywają główną rolę. τ = T/A_t ; A_t - całk. Pow. Przekroju obciążona siłą T.

Przyjmujemy założenie o równomiernym rozkładzie nacisku.

Czasem występuje docisk δd = P/A_d.

War. Wytrzymałościowe:

τ = T/A_t <= k_t; δd = P/A_d <= k_d

17. Zginanie ukośne. Zachodzi wtedy, gdy płaszczyzna obciążenia nie jest płaszczyzną głównych środkowych osi bezwładności. Ślad płaszczyzny obciążenia na poprzecznym przekroju belki nie pokrywa się wtedy z główną środkową osią bezwładności tego przekroju. Zginanie ukośne można uważać za rezultat zginania belki w dwóch płaszczyznach wzajemnie prostopadłych przechodzących przez główne środkowe osie bezwładności przekroju.
     Warunek wytrzymałości ma postać

                 

gdzie [alfa] - kąt nachylenia płaszczyzny obciążenia, Wz, Wy - wskaźniki wytrzymałości przekroju.

18. Naprężenia styczne przy zginaniu.

τ = T Sz / b Iż; T - siła tnąca, Sz - moment statyczny odciętej części przekroju względem osi obojętnej; b- szerokość przekroju na tym poziomie, dla którego obliczamy naprężenia styczne, Iz - moment bezwładności.

20. Wyprowadzić dla odcinka belki prostej obciążonej q , zależność pomiędzy M , T, q.

dT/dx = -q; dMg/dx = T; d²Mg/dx = -q

Pochodna siły poprzecznej względem współrzędnej x wzdłuż osi pręta jest równa natężeniu obciążenia ciągłego. Pochodna momentu gnącego względem x to siła poprzeczna. Druga pochodna momentu gnącego to natężenie obciążenia ciągłego.

22. Wyznaczyć równanie osi ugiętej i podać interpretację (znak).

E I y'' = -Mg

Całkujemy dwukrotnie i mamy równanie osi ugiętej. Znak jest ujemny bo przyjmujemy oś OY odwrotnie niż zwykle.

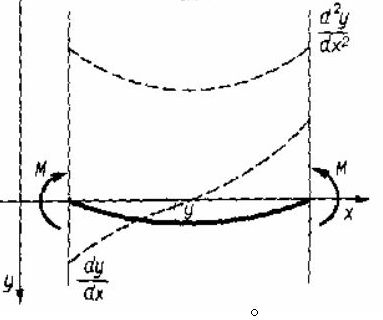
M > 0; y > 0 to d²y/dx² < 0

23. Warunki brzegowe.

Podpora stała (zamurowana).

y (x=0) = 0

y'(x=0) = 0

podpora stała i ruchoma (dla ruchomej taki sam rys.)

y(x=0) = 0

y' - nie ma założeń =/= 0

Przeguby lewy/prawy

24. Podać wytyczne w metodzie Clebscha.

1.Ten sam układ osi dla wszystkich przedziałów.

2.Jeżeli obc. ciągłe się kończy to przedłużamy je do końca belki dodając przeciwne obciążenie.

3.Całkujemy bez rozwijania nawiasów

[całka] (q/2(x-l)² = q/6 (x-l)³

4.Moment skupiony mnożymy przez współrzędną w potędze zerowej. Równanie momentów momentów momentów np. przedziału II zawiera także przedział I.

25. Stałe Ci D wyrażają kąt i przemieszczenie w miejscu przyjęcia układu współrzędnych. Wyznaczamy je z warunków brzegowych.

26. Tensor naprężeń.

Tensor naprężenia określa stan naprężenia w punkcie.

27. Wyznaczanie osi głównych głównych naprężeń stycznych.

Oś główna to taka gdzie momenty dewiacji są zero więc nie ma naprężeń stycznych. Dla każdego określonego stanu naprężeń można wyznaczyć trzy wzajemnie prostopadłe osie określające kierunki główne.

28. Niezmiennikami stanu naprężeń nazywamy wartość naprężeń głównych, które nie są zależne od przyjętego wejściowego układu osi.

gdzie:

29.Płaski stan naprężenia.

Jeżeli jedno z naprężeń głównych jest równe zeru, to stan naprężenia nazywa się płaskim; wówczas niezależnie od obranego układu osi niezmiennik sIII = 0. Jest to wystarczającym warunkiem dla stwierdzenia płaskości stanu naprę­żenia.

Macierzowa interpretacja płaskiego stanu naprężeń:

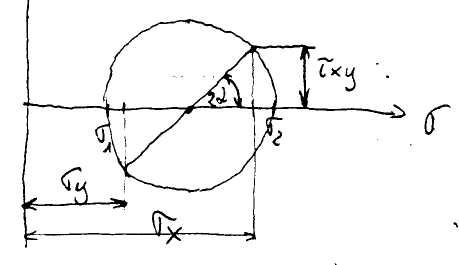
30. Koło Mohra.

31. Tensor odkształceń.

32. Niezmienniki stanu odkształcenia.

Odkształcenia główne wyznaczymy z analizy równania sekularnego odkształceń

Gdzie:

Rozwiązanie tego równania umożliwia wyznaczenie E1, E2, E3

33. Płaski stan odkształceń.

Macierz stanu odkształcenia dla układu płaskiego:

Gdzie:

Koło Mohra dla odkształceń:

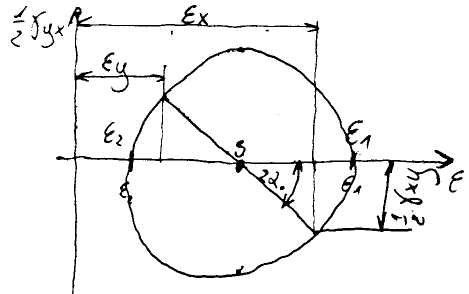
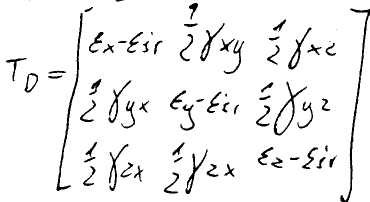
34. Tensor kulisty i dewiator stanu odkształcenia.

Tensor stanu odkształcenia jest równy sumie tensora kulistego i dewiatora.

T = Tk + Td

Tensor kulisty opisuje odkształcenie objętościowe. Tensor dewiator opisuje odkształcenie postaciowe.

35. Tensometria - zespół metod i technik pomiarowych. Przyrządy to tensometry służace do pomiaru odkształceń.
Przykład tensometru: Drut (miedz + nikiel) φd=(0,02-0,05)μm. Jeden tensometr mierzy. odkształcenia liniowe

36. Wyprowadzić zależności miedzy E G i υ

Określamy wydłużenie odpowiadające kierunkom głównym stanu naprężenia:

moduł sprężystości poprzecznej, nazywany również modułem Kirchhoffa (ma on wymiar naprężenia) i oznacza się symbolem G

37. Uogólnione prawo Hooke'a.

Stan naprężeniowy Prawo Hooke'a.

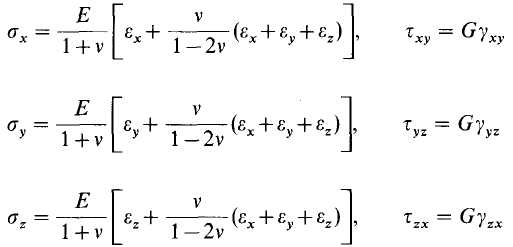
Analogicznie wzory dla Ey i Ez.

38. Moduł objętościowy ściśliwości - moduł Helmholtza

39. Związki między tensorami naprężenia i odkształcenia w złożonym stanie naprężeń

Porównaj pytania 26 i 31. Do tensorów naprężeń dodać:

40. Energia sprężysta. Przyrost energii kinetycznej ciała ΔE równa się sumie prac sił zewnętrznych L i prac sił wewnętrznych A . Praca sił wewnętrznych w materiale doskonale sprężystym jest odwracalna i określa się ją jako energie potencjalną odwracalną sił (energia sprężysta).

ΔE = L + A; A=-V; L= ΔE + V; Energia sprężysta w stanie nie odkształconym i nie naprężonym równa się zero. Energię sprężystą wyznaczamy przy założeniu że mamy do czynienia ze stanem równowagi. E=0 => V=L Energia sprężysta = pracy sił zewnętrznych. Obliczając pracę sił:

a)Energia sprężysta pręta rozciąganego siłą P.

V-energia; Właściwą energię sprężystą otrzymamy dzieląc V przez obiętośc pręta A * l.

b)Energia sprężysta ścinania.

c)Całkowita energia sprężysta.

Właściwą energię sprężystą można przedstawić jako sumę energii zmiany objętości i energii zmiany postaci.

---