LABORATORIUM FIZYCZNE			GRUPA LAB.		02
Kolejny nr ćwiczenia:	22	Nazwisko i imię:		Wydział ETI
Symbol ćwiczenia:	8	Lis Tomasz
Temat:		Data odr. ćwiczenia: 11.03.2003		Semestr	02
Wyznaczanie współczynnika załamania światła		Data odd. sprawozdania: 18.03.2003		Grupa st.	EiT 06
						Ocena
				Podpis asystenta

1. Opis ćwiczenia

Jak wykazał Maxwell światło jest częścią widma elektromagnetycznego. Wszystkie fale wchodzące w skład tego widma mają charakter elektromagnetyczny i rozchodzą się w próżni z tą samą prędkością c. Różnią się jedynie długościami fali, a więc i częstościami. W ośrodku jednorodnym i izotropowym światło rozchodzi się po linii prostej. Wektor określający kierunek rozchodzenia się światła k jest prostopadły do wektora indukcji pola magnetycznego B i do wektora pola elektrycznego E. Promienie świetlne mogą przecinać się ze sobą bez żadnych zakłóceń, a ich bieg jest odwracalny.

Jeżeli na swojej drodze promienie świetlne natrafią na ośrodek o innej gęstości, to część z nich zostanie odbita na krawędzi ośrodka, zaś część przeniknie do drugiego ośrodka ulegając załamaniu. Wiadomo, że zjawisko odbicia i załamania można opisać następującymi trzema prawami:

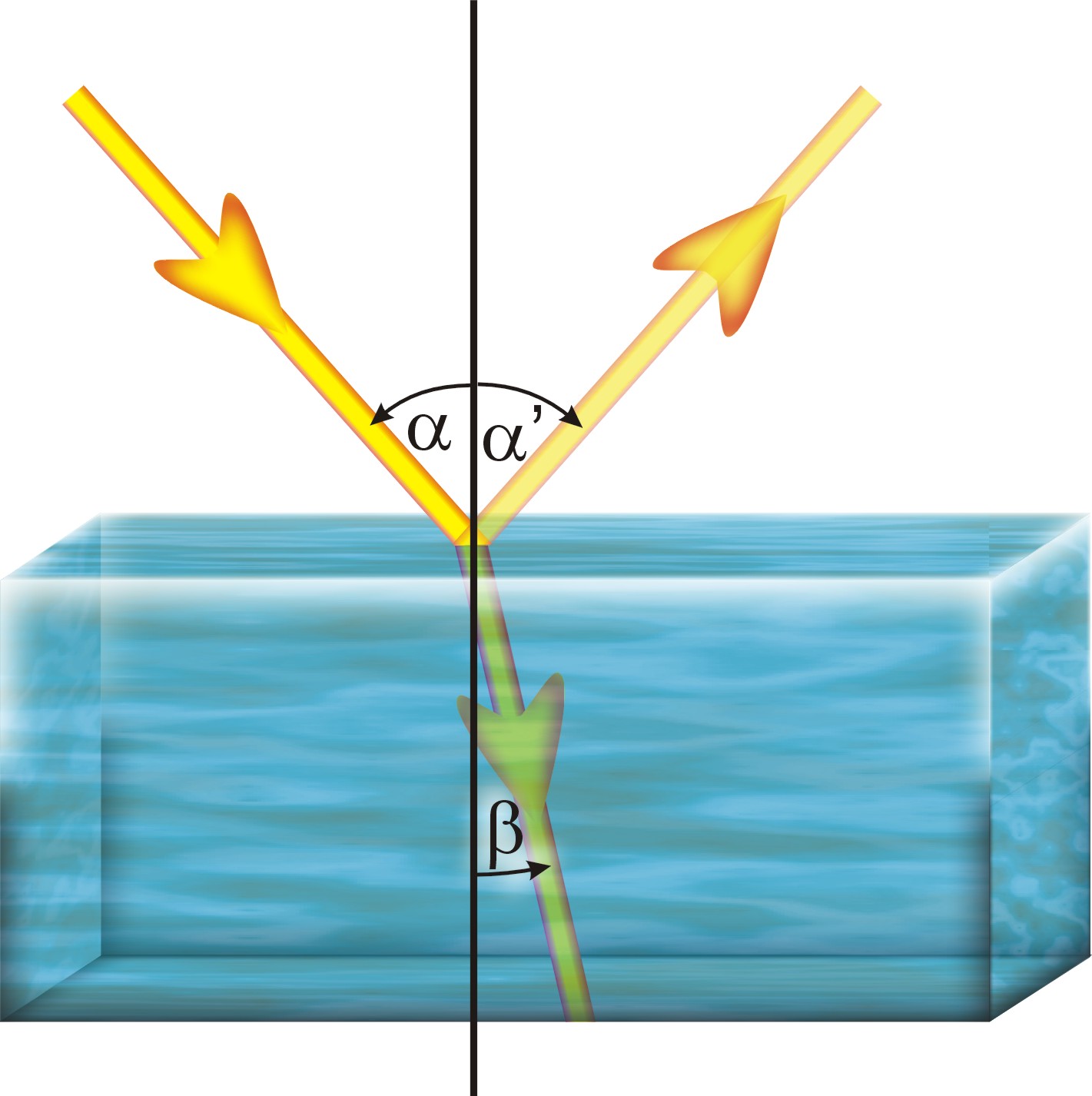
1. Promień padający, odbity i załamany oraz normalna do powierzchni granicznej leżą na jednej płaszczyźnie.

2. Kąt odbicia jest równy kątowi padania.

  '

3. Dla danych dwóch ośrodków stosunek sinusa kąta padania do sinusa kąta załamania jest równy stosunkowi prędkości wiązki w odpowiednich ośrodkach i jest stały:

Wielkość n₂₁ to tak zwany względny współczynnik załamania światła pomiędzy dwoma ośrodkami.

Jeżeli ośrodkiem pierwszym będzie próżnia (ewentualnie powietrze), to:

Wtedy n nazywamy bezwzględnym współczynnikiem załamania dla ośrodka 2. Prędkość światła zmniejsza się, jeżeli przejdzie ono z ośrodka rzadszego do gęstszego.

Podczas odbicia światło odbite i załamane ulega częściowej lub całkowitej polaryzacji. Istnieje kąt  dla którego zachodzi całkowita polaryzacja światła odbitego. Zjawisko to ma miejsce, jeżeli pomiędzy wiązką światła odbitego i wiązką światła załamanego jest kąt 90⁰. W tym przypadku kąt padania  nazywa się kątem Brewstera.

Metoda de Chaulnesa

Jeżeli obserwujemy jakiś punkt, który oddzielony jest od nas ośrodkiem o większej gęstości, np. kamień leżący na dnie jeziora, to mamy wrażenie, że znajduje się on dużo bliżej powierzchni wody, niż jest w rzeczywistości.

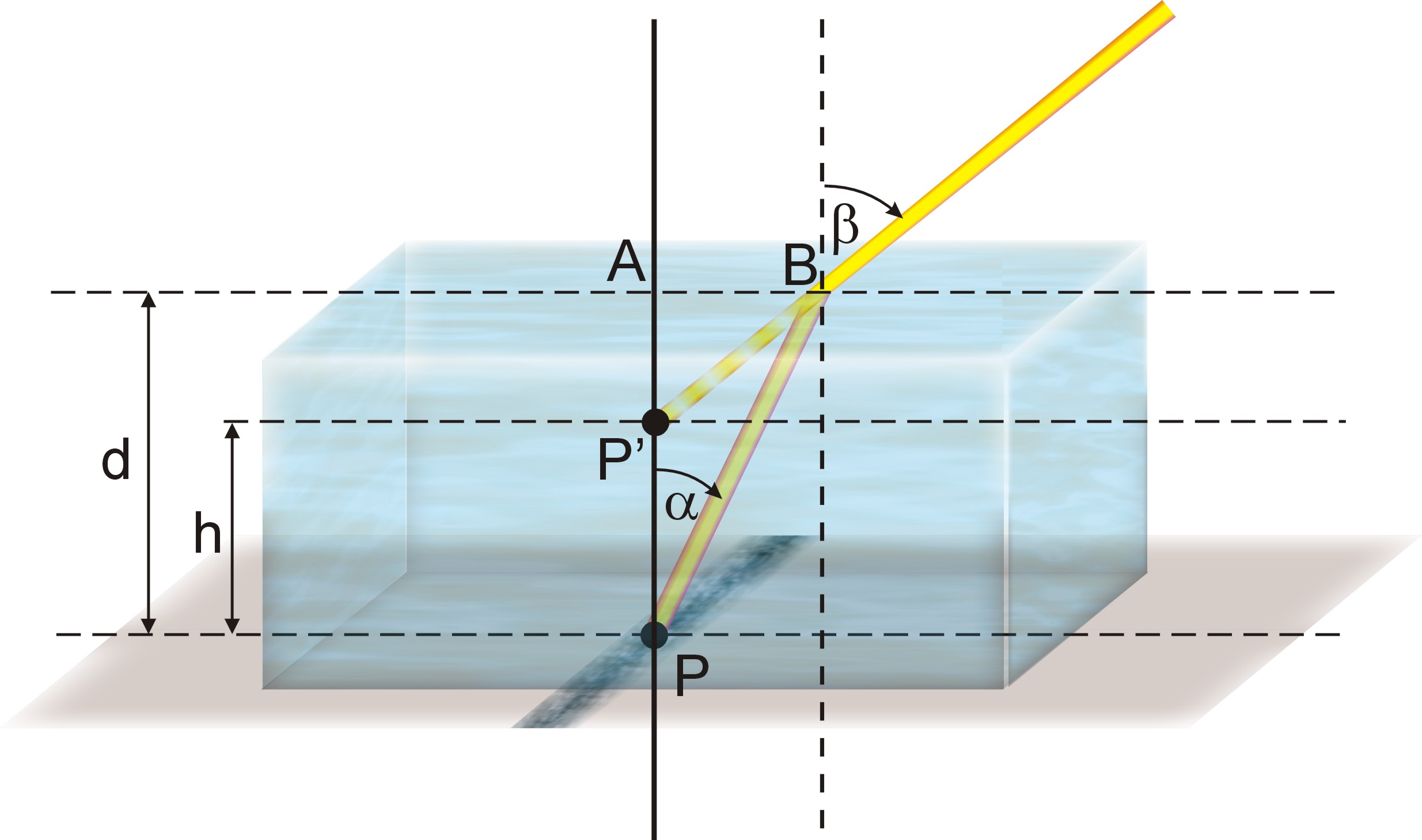
Wykorzystanie tej obserwacji może posłużyć do wyznaczenia współczynnika załamania. W doświadczeniu ośrodkiem gęstszym (badanym) były płytki płaskorównoległe. Obserwując punkt P widzimy go w położeniu P', czyli o h wyżej niż jest w rzeczywistości. Jeżeli rozpatrzyć trójkąty ABP i ABP', to podstawiając:

AB = e

AP = d

AP' = d-h

otrzymujemy:

W ten sposób, jeżeli doświadczalnie wyznaczy się wartości d i h, to można obliczyć wartość współczynnika n.

2. Wyniki pomiarów

Doświadczenia prowadziliśmy na uprzednio wybranych czterech płytkach szklanych. Badaliśmy odległości d oraz h w jednostkach niezgodnych z układem SI, jednak związanych z nim liniową zależnością. Ponieważ współczynnik załamania jest wielkością bezwymiarową, nie było potrzeby tworzenia przelicznika jednostek. Wielkości mierzone mamy więc w specyficznych jednostkach związanych z mikroskopem. Oznaczymy je przez [Jm].

	Szkło nr 1			Szkło nr 2			Szkło nr 3			Szkło nr 4
	h1 [Jm]	d1 [Jm]		h2 [Jm]	d2 [Jm]		h3 [Jm]	d3 [Jm]		h4 [Jm]	d4 [Jm]
Pomiar 1	62	190		66	197		56	190		82	252
Pomiar 2	64	195		62	195		65	204		80	249
Pomiar 3	63	192		64	198		58	195		78	248
Pomiar 4	63	192		65	196		59	196		83	251
Średnia	63	192,25		64,25	196,5		59,5	196,25		80,75	250

3. Obliczenia

Podstawiając wartości średnie otrzymamy:

1,487427
1,485822

1,435101
1,477105

4. Wyznaczanie błędów

Podczas pomiarów ustaliliśmy wielkość niepewności wzorcowania i eksperymentatora:

3 [Jm]

1 [Jm]

oraz ustaliliśmy, iż są one takie same dla wszystkich mierzonych płytek. Stąd niepewności wartości mierzonych:

1,825742

1,825742

Teraz możemy wyznaczyć niepewności współczynników załamania ze wzoru:

Podstawiając otrzymujemy:

S_n1 = 0,02211

S_n2 = 0,021581

S_n3 = 0,020021

S_n4 = 0,016744

5. Zestawienie wyników

6. Wnioski

Niestety badane przez nas płytki okazały się mieć bardzo zbliżone współczynniki załamania. Na wykresie widać, że nawet grubość płytek nie była zbyt zróżnicowana. Dokładność pomiaru jest niewielka i 3 płytki są w zasadzie nierozróżnialne. Jedynie płytka nr 3 w widocznym stopniu odbiega od pozostałych grubością i współczynnikiem załamania. Metoda de Chaulnesa nie pozwoliła więc na dokładne określenie współczynnika n. Wzrokowe badanie ostrości przyczyniło się do dużego błędu pomiaru.

---