Tomasz Pajączkowski

17.10.2001

Ćwiczenie nr 24.

Temat: Badanie obwodu RLC.

1. Tabele zebranych wartości:

dla C₁ dla C₂

ν1 [ kHz ]	I [ mA ]		ν2 [ kHz ]	I [ mA ]
400	0,20		800	0,50
410	0,20		820	0,50
420	0,20		840	0,60
430	0,20		860	0,70
440	0,20		880	0,90
450	0,25		900	1,00
460	0,25		920	1,35
470	0,45		940	1,65
480	0,50		960	2,00
490	0,60		980	2,60
500	0,70		1000	3,30
510	0,70		1020	4,25
520	0,75		1040	5,50
530	0,80		1060	6,50
540	0,85		1080	7,80
550	1,00		1100	8,90
560	1,05		1120	9,60
570	1,15		1140	10,00
580	1,35		1160	10,00
590	1,55		1180	10,00
600	1,80		1200	9,75
610	2,00		1220	9,35
620	2,40		1240	8,50
630	2,90		1260	7,80
640	3,50		1280	7,25
650	4,15		1300	6,40
660	4,85		1320	6,00
670	6,00		1340	5,35
680	7,05		1360	4,50
690	8,25		1380	4,25
700	9,60		1400	4,00
710	10,90		1420	3,50
720	12,00		1440	3,25
730	13,00		1460	2,90
740	13,80		1480	2,70
750	14,20		1500	2,40
760	14,90		1520	2,30
770	15,00		1540	2,20
780	14,50		1560	2,00
790	14,00		1580	1,90
800	13,15		1600	1,80
810	12,50		1620	1,75
820	11,50		1640	1,60
830	10,80		1660	1,50
840	9,80		1680	1,50
850	8,60		1700	1,40

3. Teoria zjawiska.

W obwodach elektrycznych zawierających dowolną kombinację połączeń oporników, cewek i kondensatorów mogą mieć miejsce drgania wymuszone. Ten rodzaj drgań występuje wówczas, gdy obwód dołączony jest do źródła, którego SEM zmienia się okresowo w czasie. Najczęściej spotykanym wymuszeniem jest pobudzenie sinusoidalne. Drgania napięć prądów i ładunków są wówczas również sinusoidalne i mają częstotliwość równą częstotliwości wymuszającej SEM. Ich amplitudy i fazy początkowe zależą nie tylko od amplitudy i częstotliwości SEM, lecz również od wartości parametrów obwodu.

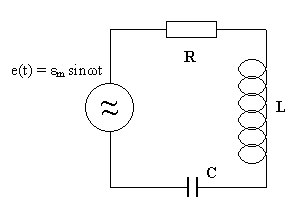
Rozważmy teraz drgania wymuszone w obwodu RLC ( przedstawionego na poniższym schemacie ). Przypuśćmy, że dane są wartości elementów R, L, C oraz wymuszenie e(t) = ε_m sinωt, a poszukujemy amplitudy i fazy początkowej drgań wymuszonych prądu i(t) = I_m sin(ωt + α).

Rozwiązanie wygodnie jest rozpocząć od założenia wielkości prądu I_m. Amplitudy napięć wynoszą odpowiednio U_R = I_mR, U_L = ωLI_m, U_C = I_m/ωC. SEM jest równe sumie tych napięć, a więc ma amplitudę i fazę ( względem I_m ) odpowiednio równe:

ε_m = [ U_R² + ( U_L - U_C )² ]^1/2 = I_m [ R² + ( ωL - 1/ωC )² ]^1/2

tgβ = ( U_L - U_C )/U_R = ( ωL - 1/ωC )/R

Stąd wyznaczona amplituda i faza prądu ( względem SEM - który był wielkością daną ) wynosi:

I_m = E_m/(( R² + ( ωL - 1/ωC )² )^1/2

tgα = -( ωL - 1/ωC )/R

Amplituda prądu zależy od częstotliwości wymuszającej SEM w sposób określony powyższą funkcją. Przy małych oraz przy wielkich częstotliwościach amplituda drgań wymuszonych jest mała, natomiast przy pewnej częstotliwości osiąga ona wartość największą. Częstotliwość ta nazywa się częstotliwością rezonansową, gdyż przy tej częstotliwości zachodzi zjawisko rezonansu. Częstość rezonansową wyznacza się z warunku dI_m/dω = 0, który w naszym przypadku sprowadza się do znalezienia minimum mianownika we wzorze (1). Wymaga to, by wyrażenie w nawiasie było równe zero: ω_rL - 1/( ω_rC ) = 0; stąd ω_r = 1/( LC )^1/2.

Ładowanie przewodnika polega na dostarczaniu mu ładunku, przy czym w procesie ładowania potencjał tego przewodnika zwiększa się co do wartości bezwzględnej. Wiele doświadczeń potwierdza, że wartość potencjału przewodnika jest proporcjonalna do dostarczonego mu ładunku. W takim razie iloczyn q/V będzie dla danego przewodnika wielkością charakterystyczną; nazywa się go pojemnością tego pojedynczego ( izolowanego ) przewodnika ( C = q/V ) i wyraża się ją w faradach.

Praktyczne znaczenie mają nie tyle pojedyncze przewodniki, co ich układy tworzące kondensatory. Kondensator stanowią dwa przewodniki o dowolnym kształcie i wymiarach, które ładuje się równymi ładunkami o przeciwnych znakach. Ważna jest wtedy nie wartość potencjału poszczególnych przewodników, lecz ich różnica, czyli napięcie między nimi. Jeśli zwiększać ładunki na dwóch przewodnikach tworzących kondensator, to zwiększa się napięcie między nimi i to - jak się okazuje z doświadczenia - proporcjonalnie do wartości ładunku. Inaczej mówiąc iloraz q/U pozostaje stały. Jest to więc wielkość charakterystyczna dla danego kondensatora; nazywa się ją pojemnością kondensatora i mierzy w faradach.

C = q/U

Prąd elektryczny płynący w dowolnym obwodzie wytwarza przenikający ten obwód strumień magnetyczny Ψ. Przy zmianach I zmienia się także Ψ, a więc w obwodzie indukuje się SEM. Zjawisko to nosi nazwę samoindukcji.

Zgodnie z prawem Biota - Savarta indukcja magnetyczna B jest proporcjonalna do natężenia prądu, który to pole wywołuje. Wynika stąd, że prąd I w obwodzie i wytwarzany przezeń strumień magnetyczny Ψ przez powierzchnię obwodu są wzajemnie proporcjonalne: Ψ = LI.

Współczynnik proporcjonalności L między natężeniem prądu i całkowitym strumieniem magnetycznym nazywa się indukcyjnością obwodu.

4. Wyprowadzenie wzorów roboczych.

Dla układu z kondensatorami C₁ i C₂ możemy wypisać zależności:

ω₁ = ( L·( C₁ + C₀ ))^-1/2 ω₂ = ( L·( C₂ + C₀ ))^-1/2

2Πν₁ = ( L·( C₁ + C₀ ))^-1/2 2Πν₂ = ( L·( C₂ + C₀ ))^-1/2

4Π²ν₁² = 1/( L·( C₁ + C₀ )) 4Π²ν₂² = 1/( L·( C₂ + C₀ ))

Wyznaczając L z powyższych wzorów i przyrównując otrzymamy:

L = 1/( ν₁²( C₁ + C₀ )) = 1/( ν₂²( C₂ + C₀ ))

( ν₂/ν₁ )² = ( C₁ + C₀ )/ ( C₂ + C₀ )

C₂( ν₂/ν₁ )² + C₀( ν₂/ν₁ )² = C₁ + C₀

C₀ ( ν₂/ν₁ )² - C₀ = C₁ - C₂( ν₂/ν₁ )²

Po przekształceniu powyższej zależności otrzymujemy równanie pozwalające wyznaczyć pojemność właściwa obwodu.

C₀ = ( C₁ - C₂( ν₂/ν₁ )² )/( ( ν₂/ν₁ )² -1 )

Indukcyjność cewki wyznaczamy z zależności wyprowadzonej w sposób następujący:

ω₁ = 2Πν₁ ω₁ = ( L·( C₁ + C₀ ))^-1/2

2Πν₁ = ( L·( C₁ + C₀ ))^-1/2

4Π²ν₁² = ( L·( C₁ + C₀ ))

L = 1/4Π²ν₁²( L·( C₁ + C₀ ))

5. Opis wykonanego ćwiczenia.

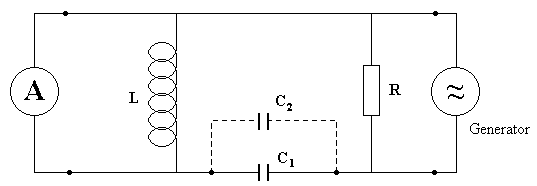
Celem powyższego ćwiczenia było wyznaczenie pojemności własnej obwodu i indukcyjności cewki dla badanego obwodu RLC. Schemat układu pomiarowego pokazany został na poniższym rysunku.

Dla poniższego układu pomiar sprowadza się do wyznaczenia wskazań mikroamperomierza przy zmieniającej się częstości generowanych drgań własnych układu z podłączonym kondensatorem C₁, a następnie z kondensatorem C₂. Przy czym w pierwszym przypadku wartość generowanych drgań zmieniała się od 400 kHz do 850 kHz ( co 10 kHz ), a w drugim od 800 kHz do 1700 kHz ( co 20 kHz ).

Uzyskane w ten sposób wartości zebrałem w powyższej tabeli, a następnie na ich podstawie dokonałem poniższych obliczeń i wyciągnąłem końcowe wnioski.

Schemat badanego układu pomiarowego:

6. Obliczenia do ćwiczenia.

Po podstawieniu odpowiednich wartości do zależności (1) i (2) wyprowadzonych powyżej otrzymałem:

C₀ = 4,419·10^-11 F

L = 7,709·10^-5 H

[ Działanie na jednostkach: 1/(Hz² F) = 1/((1/s)²(C/V)) = 1/((1/s²)(A s/V) = V·s/A = H ]

Wartości ν₁ i ν₂ odczytane z krzywych rezonansowych, dołączonych do opracowania ćwiczenia, wynoszą odpowiednio: 770 kHz i 1160 kHz.

Szacowanie niepewności pomiaru:

dla C₀

∂C₀/∂C₁ = 1/((ν₂/ν₁)²-1) = 0,788

∂C₀/∂C₂ = -(ν₂/ν₁)²/((ν₂/ν₁)²-1) = -1,788

∂C₀/∂Δν = [(-2C₂Δν(Δν²-1)-2Δν(C₁-C₂Δν²)]/(Δν²-1)² = -7,998·10^-12 [As²(1+s²)/V]

U(C) = 5,77·10^-13 F

U(Δν) = 0,577 Hz

U(C₀) = [ (∂C₀/∂C₁)²·U²(C₁) + (∂C₀/∂C₂)²·U²(C₂) + (∂C₀/∂Δν)²·U²(Δν) ]^1/2 = 4,75·10^-12 F

dla α = 0,95 U_C(C₀) = 2· U(C₀) = 0,95·10^-11 F

dla L

∂L/∂ν = -1/(2Π² ν₁³(C₀ + C₁) = -2,00·10^-10 [s²V/A]

∂L/∂C₀ = -1/(4Π² ν₁²C₀² ) = -21878160,8 [V/A]

∂L/∂C₁ = -1/(4Π² ν₁²C₁² ) = -164255,0 [V/A]

U(L) = [ (∂L/∂C₀)²·U²(C₀) + (∂L/∂C₁)²·U²(C₁) + (∂L/∂ν)²·U²(ν) ]^1/2 = 1,22·10^-5 H

dla α = 0,95 U_C(L) = 2· U(L) = 2,44·10^-5 H

7. Wnioski:

Wyznaczone wartości pojemności właściwej obwodu i indukcyjności cewki w badanym obwodzie RLC wynoszą odpowiednio: C₀ = ( 4,42 ± 0,95 )·10^-11 F , L =( 7,71 ± 2,44 )·10^-5 H.

Ewentualne błędy przy wyznaczaniu powyższych wartości wynikać mogą z nieuwzględnienia oporów wewnętrznych układu, zmieniającej się temperatury układu w czasie pomiaru i błędu w odczycie wartości ν₁ i ν₂ na podstawie krzywych rezonansu.

---