Wyznaczanie współczynnika samoindukcji cewki

i pojemności kondensatora

(ćwiczenie nr 44)

1. WSTĘP

Cele ćwiczenia:

• wyznaczenie rezystancji R_i cewki (1),

• wyznaczenie impedancji Z_i obwodu z cewką i współczynnika samoindukcji L_i cewki (2),

• wyznaczenie impedancji Z_i obwodu (3) i pojemności C_i kondensatora.

Elementy układów doświadczalnych:

• amperomierz,

• woltomierz,

• cewka,

• kondensator,

• zasilacz prądu zmiennego i przewody elektryczne.

Schematy układów doświadczalnych:

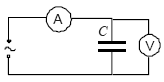
(1) (2) (3)

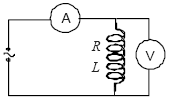
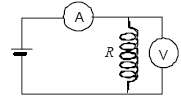
Mierzone na obwodzie przedstawionym na schemacie (1) napięcia i natężenia prądu pozwalają wykazać, że cewka wykazuje inne „właściwości” w obwodzie prądu stałego, a inne w obwodzie prądu zmiennego (2).

Na zwojnicy włączonej do obwodu prądu zmiennego indukuje się siła elektromotoryczna, która - w uproszczeniu, zgodnie z regułą Lenza - wytwarza dodatkowy opór (induktancja). Przez to dla tej samej cewki wartość impedancji (przy prądzie zmiennym) jest znacznie wyższa, niż wartość rezystancji (przy prądzie stałym).

Dla obwodu (3) „zmiennymi” czynnikami wpływającymi na wartość impedancji są pojemność kondensatora C oraz częstotliwość zmian prądu. Ich wartości są odwrotnie proporcjonalne do wartości istniejącego na kondensatorze oporu pojemnościowego R_c.

Pomiary napięć i natężeń w przedstawionych na schematach obwodach pozwalają obliczyć wartości (1) oporu, (2) impedancji i współczynnika samoindukcji cewki L_i oraz wartość impedancji i pojemności kondensatora.

2. OBLICZENIA

1. Wyznaczanie rezystancji R_i (i = 1, 2, 3) cewki.

R_i = U_i / I_i

R₁ = = 6100 Ω

R₂ = = 5967,74 Ω

R₃ = = 5880,95 Ω

2. Wyznaczanie impedancji Z_i­ (i = 1, 2, 3) obwodu z cewką.

Z_i = U_i / I_i

Z₁ = = 17428,57 Ω

Z₂ = = 16818,18 Ω

Z₃ = = 16333,33 Ω

Wyznaczanie współczynnika samoindukcji L_i (i =1, 2, 3 oraz wartości średniej L) cewki.

L_i =

ω = 2 ∙ π ∙ f

f = 50 Hz

ω = 2 ∙ 3,14 ∙ 50 Hz = 314

L₁ =

L₁ = = 51,99 H

L₂ =

L₂ = = 50,076 H

L₃ =

L₃ = = 48,53 H

L =

L = = 50,2 H

3. Wyznaczanie impedancji Z_i (i = 1, 2, 3) obwodu z kondensatorem.

Z_i = U_i / I_i

Z₁ = = 677,78 Ω

Z₂ = = 677,66 Ω

Z₃ = = 674,93 Ω

Wyznaczanie pojemności C_i (i = 1, 2, 3 oraz wartości średniej C) kondensatora.

C_i =

C₁ =

C₁ = ( 314 ∙ 677,78 Ω )^-1 = 4,7 ∙ 10^-6 F

C₂ =

C₂ = ( 314 ∙ 677,66 Ω)^-1 = 4,7 ∙ 10^-6 F

C₃ =

C₃ = ( 314 ∙ 674,93 Ω)^-1 = 4,72 ∙ 10^-6 F

C =

C = = 4,707 ∙ 10^-6 F

3. RACHUNEK BŁĘDÓW

1. Błędy pomiaru napięć i natężeń (zaokrąglane w górę):

Cewka w obwodzie prądu stałego.

ΔU₁ = ( 1% ∙ 12,2 + 0,5) V = 0,63 V

ΔI₁ = ( 1% ∙ 0,002 + 0,0005) A = 5,2 ∙ 10^-4 A

Cewka w obwodzie prądu zmiennego.

ΔU₁ = ( 1,5% ∙ 12,2 + 0,5) V = 0,69 V

ΔI₁ = ( 1,5% ∙ 0,0007 + 0,0005) A = 5,11 ∙ 10^-4 A

Kondensator w obwodzie prądu zmiennego.

ΔU₁ = ( 1,5% ∙ 12,2 + 0,5) V = 0,69 V

ΔI₁ = ( 1,5% ∙ 0,018 + 0,0005) A = 7,7 ∙ 10^-4 A

2. Błędy obliczonych wielkości.

Rezystancja cewki (1).

ΔR₁ = R₁ ( + )

ΔR₁ = 6100 Ω ( + ) = 1901 Ω

Impedancja obwodu (2).

ΔZ₁ = Z₁ ( + )

ΔZ₁ = 17428,57 Ω ( + ) = 13708,57 Ω

Impedancja obwodu (3).

ΔZ₁ = Z₁ ( + )

ΔZ₁ = 677,78 Ω ( + ) = 67,33 Ω

Współczynnik samoindukcji L (2)

ΔL₁ = (Z₁ ∙ ΔZ₁ + R₁ ∙ ΔR₁)

ΔL₁ = ∙ ( 17428,57 Ω ∙ 13708,57 Ω + 6100 Ω ∙ 1901 Ω) = 48,87 H

Pojemność kondensatora C (3)

ΔC₁ = C₁

ΔC₁ = 4,7 ∙ 10^-6 F ∙

ΔC₁ = 4,67 ∙ 10^-7 F

3. Błędy bezwzględne:

B_b1 =

B_b1 = = 0,94

B_b2 =

B_b2 = = 0,099

4. Błędy bezwzględne procentowe:

B_%1 = B_b1 ∙ 100%

B_%1 = 94 %

B_%2 = B_b2 ∙ 100%

B_%2 = 9,93%

4. WYNIKI DOŚWIADCZENIA. WNIOSKI.

1. Wynikająca z obliczeń średnia wartość współczynnika samoindukcji L cewki wynosi:

L = 50,2 H

Wartość tej samej wielkości wynikająca z pierwszej serii pomiarów wynosi:

L₁ = 51,99 H +/- 48,87 H

2. Wynikająca z obliczeń średnia wartość pojemności C kondensatora wynosi:

C = 4,707 F ∙ 10^-6

Wartość tej samej wielkości wynikająca z pierwszej serii pomiarów wynosi:

C₁ = 4,7 ∙ 10^-6 F +/- 4,67 ∙ 10^-7 F

3. Uwagi.

Wartość błędów - liczonych zgodnie z zaleceniem - pomiarowych dla napięcia, a przede wszystkim natężenia powoduje, iż błędy dla rezystancji (1) i impedancji (2) - a w konsekwencji także dla współczynnika samoindukcji cewki - praktycznie przekreślają sens wykonywania pierwszej części doświadczenia.

Dla wartości średnich L i C nie zostały policzone błędy - według skryptu należy liczyć wyłącznie błędy dla jednego z trzech pomiarów, a nie dla wartości średniej z wszystkich.

5,5/7 punktów. Błąd w nazewnictwie błędów. Nie podobały się też wnioski, z niewiadomych przyczyn.

Źródło: http://kf.sggw.pl/cwiczenia/O_EX44.pdf

---