TEMAT : REZONANS NAPIĘĆ .
IMIĘ I NAZWISKO : TOMASZ ZADROŻNY
WYDZIAŁ : Informatyka	SEMESTR : letni	ROK AKADEMICKI: 1998/99
ZESPÓŁ : nr 7	DATA WYKONANIA : marzec 1998 r.
OCENA :	PODPIS :

1. Zagadnienia teoretyczne .

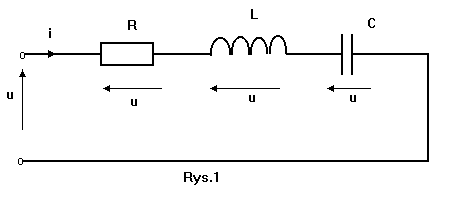
Rys. 1 przedstawia obwód szeregowo połączonych elementów R, L, C zasilanych napięciem zmiennym.

Zgodnie z II prawem Kirchoffa możemy zapisać:

lub:

gdzie

Rozwiązanie tego równania poszukujemy w postaci:

Obliczając:

końcowy wynik otrzymamy w postaci:

Dodawanie napięć o tej samej częstotliwości można wykonać metodą wykresów wektorowych. Każdy z występujących w równaniu spadków napięć traktujemy jak drgania harmoniczne różniące się od siebie jedynie fazą początkową. Na rys. 2 zaznaczono na osi odciętych amplitudę spadku napięcia na oporze R. Na osi rzędnych odkładamy amplitudy wektorów U_L i U_C (cewka i kondensator), które różnią się odpowiednio o 90 i -90 w fazie względem napięcia na rezystorze. Z tego modelu wektorowego otrzymujemy:

oraz

Wielkość Z nazywamy impedancją lub oporem pozornym obwodu prądu zmiennego.

Rezonans napięć zachodzi wtedy gdy reaktancja wypadkowa X = 0 . To znaczy :

Wtedy impedancja obwodu jest najmniejsza i równa rezystancji . W przypadku tym natężenie prądu osiąga maksymalną wartość i jest w tej samej fazie co przyłożone napięcie . W przypadku tym napięcia U_l i U_C są sobie równe i mogą znacznie przewyższać napięcie zasilające jest to tzw. przepięcie .

Wartość tego przepięcia określona jest stosunkiem napięcia na cewce lub na kondensatorze do napięcia zasilającego :

Wielkość Q nazywana również dobrocią obwodu rezonansowego , jest tym większa , im mniejszy jest opór omowy R obwodu .

Na podstawie prawa Ohma można wyznaczyć współczynnik samoindukcji cewki L :

stąd :

2. CEL ĆWICZENIA .

Naszym zadaniem było zbadanie rezonansu napięć w prostym obwodzie . Wyniki otrzymywaliśmy zmieniając wartość pojemności . Celem tego ćwiczenia jest obliczenie na podstawie pomiarów indukcyjności oraz dobroci obwodu , i wykreślenie charakterystyk napięciowych i prądowych .

3. POMIARY .

PARAMETRY :

U = 14,74 V

f = 50 Hz

R1 = 226 Ω

R2 = 603 Ω

Tabela pomiarów:

UL UC I

C [nF]	R=0	R=R1 [V]	R=R2	R=0	R=R1 [V]	R=R2	R=0	R=R1 [mA]	R=R2
200	7	6	6	20	20	20	1,0	1,0	1,0
250	10	10	10	25	24	22,5	2,0	2,0	1,5
280	12	12	12	26	26	26	2,5	2,5	2,5
320	16	18	16	30	30	30	3,0	3,0	3,0
370	25	24	24	38	38	36	5,5	5,5	5,0
400	34	32	30	47	44	42	7,5	7,5	6,5
480	90	70	54	100	80	60	20,0	16,0	12,5
510	105	84	60	122	90	64	25,0	19,0	13,5
540	130	94	64	130	94	64	28,5	21,0	15,0
580	110	86	62	100	80	58	29,0	20,0	14,5
600	96	79	60	85	70	54	22,0	18,0	14,0
640	74	66	54	62	55	46	18,5	16,0	12,5
680	62	56	48	50	45	40	15,0	13,5	11,5
720	52	49	42	39	36	32	13,0	12,0	10,5
780	44	42	38	30	30	28	11,0	10,5	9,5
800	42	40	36	29	28	26	10,5	10,0	9,0

4. WNIOSKI .

Na powyższych wykresach widzimy, że jedną z ważniejszych cech obwodu rezonansowego jest jego dobroć. Im dobroć obwodu jest większa tym większe jest napięcie na elementach biernych w stosunku do napięcia na rezystancji, czyli na całym obwodzie. W związku z tym wartość prądu również jest większa, co widać na wykresach. Zjawisko zwiększenia napięcia na elementach biernych w stosunku napięcia całkowitego nosi nazwę przepięcia. Zjawisko to jest bardzo niebezpieczne. Przy dużych wartościach dobroci napięcie na elementach biernych może być tak duże, że spowoduje uszkodzenie izolacji mimo niskiego napięcia zasilającego.

---