1. Co to jest grafika komputerowa, przetwarzanie obrazu i rozpoznawanie obrazu

Grafika komputerowa to tworzenie obrazów na podstawie informacji opisowej. Posiada szerokie zastosowanie, także przy tworzeniu symulatorów oraz w przemyśle militarnym. Przetwarzanie obrazów dotyczy zagadnień, w których dane wejściowe jak i wyjściowe to obrazy - usuwanie zakłóceń, poprawa jakości obrazów, filtrowanie, kompresja, redukcja obrazów do konturów czy figur kreskowych, tworzenie przekrojów. Rozpoznawanie obrazów - tworzenie ich opisów, kwalifikowanie do pewnej, szczególnej klasy. W wyniku analizy obrazu powstaje opis matematyczny, ciąg symboli lub graf. Dalsze przetwarzanie tych danych pozwala na wyciąganie wniosków analitycznych.

2. Napisać program wyznaczający histogram rozkładu jasności obrazu kolorowego o 24-bitowej strukturze pixela.

Struct pixel

{

char r;

char g;

char b;

};

…

pixel obraz[M][N];

int hisR[256] = 0;

int hisG[256] = 0;

int hisB[256] = 0;

int histogram [511] = 0;

int row, col, i;

for(row = 0; row < M, row++)

{

for(col = 0; col<N; col++)

{

hisR[(int) obraz[row,col].r]++;

hisG[(int) obraz[row,col].g]++;

hisB[(int) obraz[row,col].b]++;

histogram[(int) max(obraz[row,col].r, obraz[row,col].g, obraz[row,col].b)+

min( obraz[row,col].r, obraz[row,col].g, obraz[row,col].b)]++;

}

}

3. Omówić poprawę jakości obrazu poprzez modelowanie histogramu/korekcję tonalną/filtrowanie przestrzenne

-KOREKCJA TONALNA - operacja punktowa, w wyniku której można wykonać rozjaśnienie, przyciemnienie obrazu, obniżenie i zwiększenie kontrastu. Stosujemy tutaj przekształcenia krzywej odwzorowań tonów - krzywej, która początkowo jest linią prostą nachyloną pod kątem 45^O. Na osi poziomek zaznaczone są poziomy jasności obrazu wejściowego, a na pionowej obrazu wyjściowego. Korekcja tonalna liniowa - krzywa odwzorowań tonów ma postać linii prostej (łamanej), nachylonej do osi poziomej pod pewnym kątem. Wadą korekcji liniowej jest możliwość obcięcia pixeli końcowych w obszarze cieni lub świateł. Przy rozjaśnieniu części jasnych pixel staje się zupełnie jasny, przy przyciemnianiu widać zanikanie pixeli ciemnych - zanik szczegółów. Korekcja tonalna nieliniowa jest wolna od tych wad.

-MODELOWANIE HISTOGRAMU - histogram to graficzne przedstawienie ilości udziału pixeli obrazu w poszczególnych zakresach tonalnych - jest to wykres słupkowy 256 słupków. Modelowane histogramu odbywa się poprzez rozciąganie, wyrównanie i normalizację. Rozciąganie wykonujemy, kiedy na histogramie nie występują skrajne wartości. Naszym celem jest taki rozkład na histogramie, który obejmie wszystkie poziomy. Wyrównanie histogramu polega na uzyskaniu możliwie równomiernego rozkładu poziomów jasności obrazu dla całego zakresu. Skutkiem tego jest poprawa kontrastu, podkreślenie mało widocznych szczegółów. Normalizacja zmienia zakres zmienności poziomów jasności obrazu wejściowego.

-FILTROWANIE PRZESTRZENNE - przetwarzaniu podlega funkcja jasności. Wartość jasności pixela obrazu wyjściowego obliczana jest na podstawie jasności pixeli obrazu wejściowego leżących w bezpośrednim sąsiedztwie danego pixela. W tych metodach definiowana jest maska przemieszczająca się w obrębie obrazu z krokiem równym odstępowi między pixelami i zgodnie z definicją operatora T wyznaczana jest nowa wartość dla każdego pixela obrazu.

4. Omówić kryterium wyboru pixeli w algorytmie Bresenhama kreślenia odcinka

Rysowanie opiera się na zmiennej decyzyjnej, której znak decyduje o kolejnym kroku algorytmu. Zmienna określa kierunek poziomy, pionowy lub idealnie skośny rysowania kolejnego pixela odcinka. Algorytm działa na liczbach całkowitych. Pozwala on wybrać, które pixele leżą najbliżej rasteryzowanego obiektu. Startujemy z punktu P0(0,0) (umownie). W kolejnym kroku możemy zapisać pixel (x+1, y) (ruch poziomy) lub (x+1, y+1) (ruch ukośny). Koniec następuje w punkcje PK(X,Y).

5. Omówić kryterium wyboru pixeli w algorytmie Bresenhama kreślenia okręgu.

Przy rysowaniu okręgu mamy możliwość wybrania jednego z trzech pixeli - A (x+1, y), B (x+1, y-1) lub C (x,y-1). Należy podzielić nasz okrąg na 4 jednakowe części (nie ma potrzeby wyznaczania punków aż 4 razy, okrąg jest symetryczny). Dla pierwszej ćwiartki dokonujemy podziału okręgu na dwa wycinki. Punktem podziału jest miejsce, gdzie f(x)/f(y) = 1 (współczynnik kierunkowy wektora stycznego jest równy -1). Startujemy z punktu P0 (0, R). W pierwszym wycinku wybieramy pomiędzy punktami A oraz B - głównym kierunkiem jest oś x., w drugim wycinku pomiędzy punktami B oraz C - głównym kierunkiem jest oś y. Naszym końcowym punktem jest PK(R, 0). Należy teraz tylko wykonać odpowiednie operacje przekształcające, aby naszą ćwiartkę przerobić na okrąg.

6. Omówić modelowanie powierzchni metodą Coonsa.

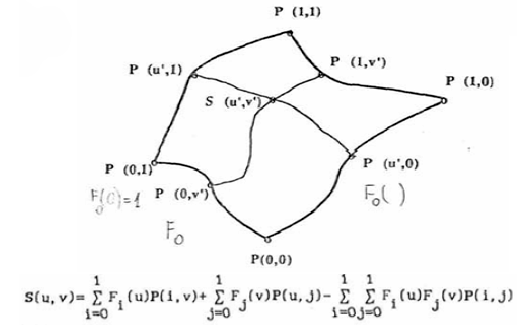
Metoda zakłada, że dane są cztery odpowiednio przecinające się krzywe definiujące brzeg wycinka powierzchni. Niech wycinek powierzchni S(u,v) będzie znormalizowany do kwadratu jednostkowego 0>=u>=1, ->=v>=1. Wycinek Coonsa buduje się interpolując jej przeciwległe brzegi.

Gdzie P(0,0) jest punktem przecięcia krzywych P(u,0) i P(0,v);

P(0,1) jest punktem przecięcia krzywych P(u,1) i P(0,v);

P(1,0) jest punktem przecięcia krzywych P(u,0), P(1,v)

P(1,1) jest punktem przecięcia krzywych P(u,1), P(1,v).

Funkcje F są to dowolne dobrane funkcje spełniające warunki:

F0(0) = 1, F0(1) = 0, F1(0)=0, F1(1) = 1, np. F0(u) = 1-u oraz F1(u) = u

7. Omówić funkcję bazową i własności krzywych Beziera, B-sklejanych i β-sklejanych.

Beziera - definiujemy poprzez łamaną kontrolną o N+1 wierzchołkach. Początkowy i końcowy punkt leżący na krzywej pokrywa się z pierwszym i ostatnim punktem kontrolnym. Krzywe te są styczne do łamanej kontrolnej w punkcie początkowym i końcowym. Umożliwia to łączenie ze sobą krzywych i powierzchni Beziera z zachowaniem ciągłości klasy C1 połączenia. Właściwości: nie przechodzą przez wszystkie punkty kontrolne, pozostają w wypukłej części łamanej kontrolnej, nie umożliwiają lokalnej kontroli kształtu, punkty kontrolne mają wpływ nie tylko na punkty leżące w najbliższym otoczeniu, lecz także na punkty na całej długości krzywej lub powierzchni. Przesunięcie dowolnego punktu kontrolnego powoduje zmianę położenia wszystkich punktów tworzących krzywą lub powierzchnię. Dla N punktów kontrolnych generowana jest krzywa N-1 stopnia. Wpływa to na złożoność obliczeniową algorytmów realizujących operacje na krzywych i powierzchniach.

B-sklejane - znana jest łamana kontrolna o N+1 wierzchołkach i określone są węzły t(i). Funkcja bazowa N_i,k(t) jest wielomianem k-1 stopnia, który zapewnia ciągłość klasy C(k-2) na całej długości definiowanej krzywej. Wartość krzywej zależy od położenia węzłów t(i) oraz t(i+k). Modyfikacja punktu kontrolnego zmienia lokalnie kształt krzywej. Kształt krzywej może być modyfikowany poprzez wielokrotne zdefiniowanie tego samego punktu kontrolnego. Stopień k funkcji bazowej wpływa na odległość krzywej od punktów definiujących. Powierzchnia B-sklejana definiowana jest iloczynem tensorowym krzywych B-sklejanych. Właściwości: definiowanie na podstawie łamanych lub grafów kontrolnych, umożliwiona lokalna kontrola kształtu tworzonej krzywej lub powierzchni, stopień k funkcji bazowej zapewnia ciągłość C(k-1) na całej długości definiowanej krzywej, gładkość powierzchni jest kontrolowana przez stopień k i 1 funkcji bazowych, stopień funkcji bazowych nie zależy od liczby punktów kontrolnych.

β-sklejane - właściwości - mogą być wykorzystywane w interakcyjnych systemach graficznych, w których wymagana jest dokładna kontrola kształtu generowanych obiektów. Kontrola kształtu oraz transformacje mogą być dokonywane lokalnie. Parametry β1 i β2 mogą być przedstawione w formacie funkcji, co umożliwia ciągłą kontrolę kształtu. Stopień bazowy funkcji β-sklejanych jest stały (3 dla krzywych i 6 dla powierzchni). Nie przechodzą przez punkty kontrolne (nawet początkowy i końcowy) Dla zapewnienia przejścia przez określony punkt kontrolny należy do łamanej kontrolnej lub grafu dołożyć dodatkowy punkt. Parametry β1 wpływa na symetrię krzywej, a β2 na stopień przylegania krzywej do łamanej kontrolnej. Jeśli β1 = 1 i β2 = 0, to funkcje bazowe β-sklejane redukują się do funkcji bazowych B-sklejanych 3-go stopnia.

8. Omówić na przykładzie funkcji biblioteki OpenGL przekształcenia geometryczne w przestrzeni 3D.

-przesunięcia - glTranslate*(x,y,z)

-skalowanie - glScale*(x,y,z)

-obrót wokół zadanej osi - glRotate*(α,x,y,z) - x,y,z - wybór osi

Gdzie * to typ przyjmowanych parametrów (np. 3f - trzy float'y)

9. Prymitywy geometryczne dostępne w bibliotece Open GL.

-GL_POINTS - punkty w przestrzeni

-GL LINES - linie wyznaczone przez dwa punkty w przestrzeni

-GL_LINE_STRIP - linie, których ostatni punkt jednej, jest pierwszym punktem kolejnej
-GL_LINE_LOOP - linie połączone razem w jedną bryłę

-GL_POLYGON - wielokąty

-GL_QUADS - czworościany

-GL_QUAD_STRIP - czworościany, w których ostatnia krawędź jednego jest kolejną krawędzią następnego

-GL_TRIANGLES - trójkąty

-GL_TRIANGLE_STRIP - trójkąty, w których ostatnia krawędź jednego trójkąta jest pierwszą krawędzią kolejnego trójkąta

-GL_TRIANGLE_FAN - trójkąty posiadające jeden, centralnie umieszczony wierzchołek, posiadające wspólne ściany

11. Narysować i opisać model procesu rzutowania 3D.

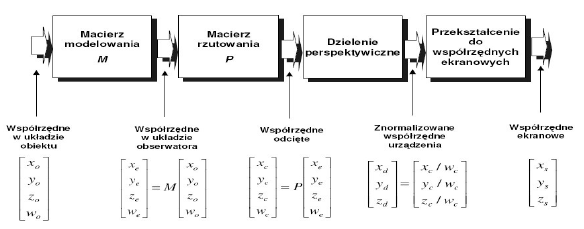
Wejście - modele obiektów 3D.

1. Macierz modelowania sceny: układ wsp. rzeczywistych, ziemskich - translacja, skalowanie, obrót

2. Macierz rzutowania: układ wsp. płaszczyzny rzutowania - rzut perspektywiczny, ortogonalny

3. Przekształcenia normalizujące: układ wsp. urządzenia zobrazowania, wsp. pixelowe

4. Definiowanie okna zobrazowania (ukł. Wsp. obszaru zobrazowania, wsp. ekranowe)

Wyjście - obraz sceny w oknie zobrazowania

12. Jakie czynniki fizyczne wpływają na wrażenie koloru? Podać ich interpretację na przykładzie wykresu rozkładu energii światła w funkcji długości fali.

Barwa - fizycznie określana przez długość fali świetlnej (400-700 nm). Zależy od wartości na osi poziomej

Jasność - określana przez wielkość energii związanej z promieniowaniem (za duża powoduje uszkodzenie oka). Jasność zależy od wartości osi pionowej.

Nasycenie - stosunek różnicy energii dominującej fali świetlnej i wypadkowej energii dla pozostałych długości fal, do wartości energii dominującej fali świetlnej. (e2 - e1)/ e2. Fizycznie odpowiada ilości fal o różnej długości składających się na dany kolor.

13. Narysować i opisać model koloru CIE L*a*b*. W jakim zakresie definiuje się parametry tego modelu?

Opisywane barwy mieszają się w elipsoidzie o trzech prostopadłych osiach. Wzdłuż osi A barwy przechodzą od zielonej do czerwonej, wzdłuż B od żółtej do niebieskiej. W punkcie zbiegu jest biel. Wzdłuż osi pionowej L (jasność - 0 - 100) biegną barwy achromatyczne. Jest to najszersza gama barw, opracowana na podstawie modelu CIE Yxy. Zastosowana transformacja pozwala na łatwiejsze wyliczenie odległości pomiędzy dwoma barwami w przestrzeni. Każdy inny model da się opisać we współrzędnych CIE Lab, ale nie na odwrót. Dzięki temu model jest niezależny od urządzeń we/wy.

14. Narysować i opisać modele koloru RGB i CMY. Podać równanie konwersji RGB → CMY.

RGB - składowe to kolory czerwony, zielony i niebieski. Sześcian, w podstawie na prawo zielony, na lewo czerwony. Na najdalszym od nas, na górze wierzchołku niebieski. Czarny w 0,0,0, biały w 1,1,1. punktu 1,1,1 to górny wierzchołek przy obserwatorze.

CMY - barwy to zielono-niebieski cyjan, karmazyn - magenta i żółty. Są to dopełnienia barw RGB. W tym modelu sześciennym punkt 0,0,0 to biały, 1,1,1 to czarny (nałożenie się wszystkich barw daje czerń). Po prawo magenta, po lewo cyan, na górze, daleko od nas żółty.

Równanie konwersji RGB → CMY: C = 1-R, M = 1-G, Y = 1-B

15. Omówić model koloru CMYK. Podać równanie konwersji CMY → CMYK.

Podobny do modelu CMY, jednak w tym używany jest też kolor kluczowy, czyli czarny (Key). Zasada substraktywnego mieszania barw. Posiada szerokie zastosowanie w poligrafii. K należy do zakresu <0;1>. C - C-k*min(CMY), M = M - k*min(CMY), Y = Y - k*min(CMY). K = k*min(CMY).

16. Narysować i opisać model koloru HLS i HSV. W jakim zakresie definiuje się parametry tego modelu?

HLS - kolor definiowany za pomocą barwy H, jasności L oraz nasycenia S. Barwa związana jest bezpośrednio z długością fali promieniowania widzialnego. Jest ona reprezentowana za pomocą okręgu. Kolory podstawowe i dopełniające rozmieszczone są na okręgu tworząc sześciokąt regularny. 0^O - czerwony, 120^O - zielony, 240^O - niebieski, dopełniające do kolorów to dany kolor + 180^O. Jasność - związana ze skalą kolorów achromatycznych, definiuje wszystkie odcienie szarości od 0 (czarny) do 1 (biały). Nasycenie - ilość fal o różnej długości składających się na jeden kolor. Kolor czysty lub w pełni nasycony to 1, kolor szary utworzony za pomocą fali o szerokim przedziale długości 0. Barwa wyrażana jest jako część ułamkowa jednostkowego kąta pełnego. Dzięki temu wszystkie kolory mogą być definiowane wektorem trzech składowych <HLS>, których wartości należą do przedziału <0;1>. Model można przedstawić jako podwojony stożek o podstawie sześciokąta równobocznego. Barwa - wartość kąta wokół osi L. Jasność - współrzędna osi pionowej. Nasycenie - odległość od osi pionowej.

HSV - Barwa H, Nasycenie S, Wartość V. Przedstawia się go jako ostrosłup o podstawie sześciokąta równobocznego. Wierzchołki podstawy odpowiadają barwom spektralnym, wierzchołek barwie czarnej, środek podstawy białej. Barwy rozmieszone tak, jak w HLS. Wartość nasycenia określa względna odległość punktu od pionowej osi, dla punktów leżących na ścianie wartość = 1.

17 Operacje w przestrzeni kolorów RGB.

-zmiana jasności

-filtr kolorowy

-zwiększenie kontrastu

-utrata ostrości

-wygładzanie

-uwypuklanie

-redukcja liczby barw

-zmiana nasycenia

-zmiana barwy

-przejście na obraz monochromatyczny

-progowanie

-fotoinwersja

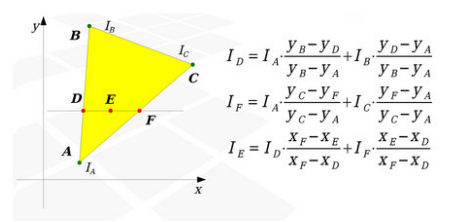
18. Cieniowanie powierzchni metodą Gourauda.

-wyznaczenie barwy w wierzchołkach trójkąta: wyznaczenie wektorów normalnych do wszystkich wierzchołków jako średniej arytmetycznej wektorów normalnych wszystkich ścian, do których należy ten wierzchołek, a następnie na podstawie wektora normalnego wyznaczenie barwy wierzchołka korzystając z wybranego modelu oświetlenia.

-liniowa interpolacja barwy dla wszystkich punktów wielokąta zgodnie z wzorami:

19. Cieniowanie powierzchni metodą Phonga.

-wyznaczenie wektorów normalnych do wszystkich wierzchołków wielokąta jako średniej arytmetycznej wektorów normalnych wszystkich ścian, do których ten wierzchołek należy.

-liniowa interpolacja wartości wektorów normalnych dla wszystkich punktów wielokąta (pixeli)

-interpolacja wzdłuż krawędzi

-interpolacja wzdłuż linio horyzontalnych

-wyznaczenie barwy dla wszystkich punktów wielokąta na podstawie wartości wektorów normalnych, zgodnie z przyjętym modelem oświetlenia.

20. Omówić zasadę generowania obrazu w projektorach CRT, LCD i DLP.

-CRT - trzy obiektywy (lampy projekcyjne). Każda z lamp daje obraz w jednej ze składowych RBG. Obraz powstaje poprzez nałożenie się na ekranie trzech składowych.

-LCD - światło z lampy jest filtrowane i rozszczepiane na trzy składowe RGB. Każda z tych składowych kierowana jest na osobną matrycę LCD, której komórki są sterowane zgodnie z wartością odpowiedniej składowej koloru pixela. Każdemu pixelowi przyporządkowana jest odpowiednia „ilość” składowej koloru. Strumienie światła kierowane są następnie na pryzmat. Tak wygenerowany obraz wyświetlany jest na ekranie za pomocą obiektywu. Jedna matryca: Swiatlo z lampy przechodzi przez pojedyncza matryce LCD. KaDdy piksel matrycy sklada sie z 3 komorek LCD z filtrami R, G i B na kaDda komorke. Wlaczenie i wylaczenie komorki jest sterowane zgodnie z wartoscia odpowiedniej skladowej koloru piksela. Strumien swiatla po przejsciu przez matryce tworzy obraz. Tak wygenerowany obraz wyswietlany jest na ekranie za posrednictwem obiektywu.

-DLP - światło z lampy jest rozszczepiane na trzy składowe EGB za pomocą wirującej z częstotliwością 60Hz tarczy z filtrami RGB. Tak powstałe wiązki kierowane są na układ DMD, który składa się z bardzo dużej ilości ruchomych mikro-lusterek (na każdy pixel jedno lusterko). Aby uzyskać różne nasycenie danej składowej, część padającego światłą jest odbijana w stronę obiektywu, a część rozpraszana zgodnie z wartością odpowiedniej składowej koloru pixela. Odbite światło przechodzi dalej przez układ optyczny. Obraz końcowy jest syntezowany przez nakładanie na przemian obrazów odpowiedzialnych za każą ze składowych RGB. Trzy układy: Projektory z 1 ukladem DMD nie daja wystarczajacej ostrości obrazu. W projektorach DLP z 3 ukladami DMD,na każdy przetwornik trafia jedna wiazka o barwie R, G lub B. Projektory takie generuja najlepszy obraz ze wszystkich urządzeń projekcyjnych. Koszt zakupu takiego urzadzenia jest kilkakrotnie wyzszy niz w wypadku zwyklych modeli DLP i wiekszosci projektorow LCD. Kompromisem sa urzadzenia z dwoma ukladami DMD, gdzie dodatkowy zestaw lusterek odpowiada za odbijanie wylacznie swiatla o barwie czerwonej.

---