AGH, Wydział EAIiE Katedra Automatyki Napędu i Urządzeń Przemysłowych				Nazwisko i Imię: Marcin Szybowski
LABORATORIUM TEORII SEROWANIA I TECHNIK REGULACJI				Semestr: IV
Rok szkolny: 2001/2002		Rok studiów: II		Grupa: 8.2
Kierunek: Elektrotechnika				Nr ćwiczenia: 7
Temat ćwiczenia: Analiza podstawowych układów dyskretnych.
Data wykonania: 28-04-2002	Data oddania: 6-05-2002		Data zaliczenia sprawozdania:

Wprowadzenie do ćwiczenia :

Ćwiczenie polegało na zapoznaniu się z układami sygnałów dyskretnych.

Układy nazywamy dyskretnymi, jeżeli istniejący w nich czas przedstawimy w postaci całkowitych liczb (zmieniających się co jedną określoną wartość). Wszystkie zatem wartości zależne od czasu będziemy odczytywali w pewnych określonych chwilach (nie uzyskamy sygnału ciągłego).

Funkcją dyskretną nazywać będziemy funkcję odwzorowującą zbiór liczb całkowitych w zbiór liczb rzeczywistych .

Do opisu układów dyskretnych stosuje się przekształcenie Z , gdyż wprowadza ono uproszczenie przy analizie opóźnienia - składnik e^-st występujący w transformacji Laplace'a zostaje zastąpiony czynnikiem z ^-1.

Przekształcenie Z wyraża się wzorem:

gdzie:

f(nT) - oryginał,

F(z) - transformata Z funkcji f(nT).

Przekształcenie to przyporządkowuje funkcji dyskretnej f(t) [f(t)>0] funkcję F(z) zmiennej zespolonej.

Transformata F(z) funkcji dyskretnej istnieje , jeżeli szereg jest zbieżny .

Transformaty F(z) istnieją dla funkcji dyskretnych , które nie rosną szybciej od funkcji wykładniczych .

Oryginał f(nT) można wyznaczyć (jedynie w chwilach impulsowania) na podstawie transformaty F(z) stosując odwrotne przekształcenie Z,

F(nT)=Z^-1[F(z)]

W przekształceniu Z można wyznaczyć funkcją czasu jedynie w chwilach próbkowania. Pomiędzy tymi chwilami nie wiemy nic o wartościach funkcji poszukiwanej. Jest to wadą przekształcenia Z.

Wykonanie ćwiczenia :

Układy były symulowane w matlabie, z użyciem modułu simulink.

Schemat blokowy układu nr 1

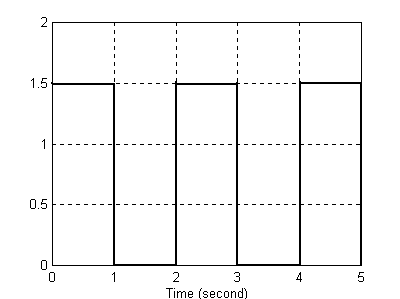
Do generatora fali prostokątnej podłączony został człon opóźnienia jednostkowego (Unit Delay). Poniżej przedstawiono sygnał wejściowy oraz sygnał wyjściowy na ekranach w postaci wykresów.

Sygnał wejściowy Sygnał wyjściowy

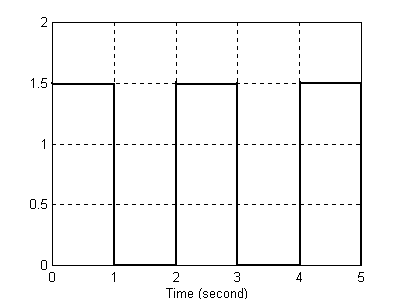
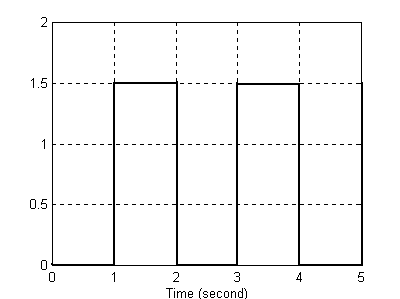
Można zaobserwować, że sygnał wyjściowy jest opóźniony względem wejściowego o 1s . Stała iteracji równa jedności pozwala nam odczytać wysokość oraz szerokość sygnału. Kłopoty z ustaleniem parametrów sygnału (szerokość oraz wysokość) pojawiają się w momencie, gdy przyjmiemy stałą próbkowania o wartości większej niż ta szerokość czy wysokość.

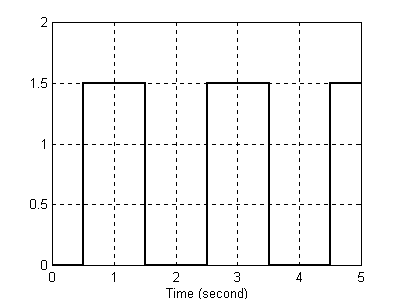
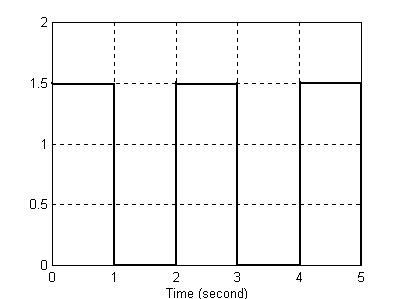
Na potwierdzenie powyższej tezy poniżej przedstawiono odpowiedzi układu przy stałej dyskretyzacji równej 0,5 oraz 2 .

T=0,5

Sygnał wejściowy Sygnał wyjściowy

T=2

Sygnał wejściowy Sygnał wyjściowy

Można zaobserwować , że z przebiegu o stałej próbkowania nie możemy

Przy stałej próbkowania równej 0,5 Matlab pobiera wartości sygnału dla t=n*0,5 , a zatem w punktach 0 ; 0,5 ; 1 ; 1,5 ... I tam właśnie powinny się pojawić impulsy o długości równej odczytanej wartości liczbowej. Funkcja jest jednak przedstawiona w postaci funkcji ciągłej gdyż przyjmujemy, że sygnałowi odpowiada odpowiednio zwielokrotniona stała iteracyjna.

Patrząc na przebieg sygnału wyjściowego dla T=0,5 widać , że przy stałej próbkowania mniejszej od szerokości sygnału możemy odtworzyć sygnał wejściowy , gdyż wtedy układ odpowiednio szybko reaguje na zmiany sygnału. W badanym bloku następuje opóźnienie sygnału o wartość stałej dyskretyzacji, a następnie zostaje on przekształcony w sposób opisany powyżej , tzn. dla t=0 jest 0 , więc w przedziale 0÷0,5 funkcja ma wartość stałą równą zero, w t=0,5 jest 1, więc w 0,5÷1 jest 1 , w t=1 jest 1, więc w 1÷1,5 jest 1 itd . Taki właśnie sygnał obserwujemy na wyjściu. I zgodnie z przewidywaniami jest on opóźniony o 0,5 s .

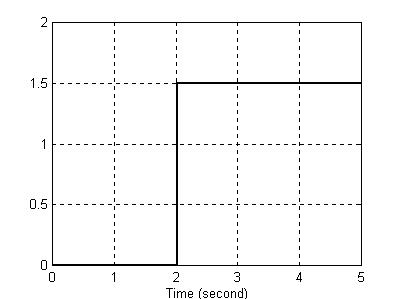
Podobnie ma się sprawa z układem w którym T=2 . Tym razem jednak nie widzi on wszystkich impulsów które zostały podane na wejście bloku . Sygnał pobieramy w t=0,2,4,6... (gdzie miał wartość 1,5) , nie biorąc pod uwagę wartości w t=1,3,5,7...(gdzie miał wartość 0) czego skutkiem w przedziale 0÷2 sygnał wyjściowy ma wartość zero (opóźnienie) , a następnie dla t=2 mamy 1,5 , więc w przedziale 2÷4 jest 1,5 , ale dla t=4 też mamy 1,5 powoduje to, iż wyjściu można zaobserwować w t=2 skok do wartości 1,5 , która to wartość utrzymuje się aż do końca zadanego czasu symulacji .

Schemat blokowy układu nr 2

Do bloku o transmitancji równej G(z) doprowadzono wymuszenie w postaci skoku jednostkowego.

Charakterystyki sygnałów wyjściowego i wyjściowego obserwowane na ekranach przedstawiono poniżej:

Sygnał wejściowy Sygnał wyjściowy

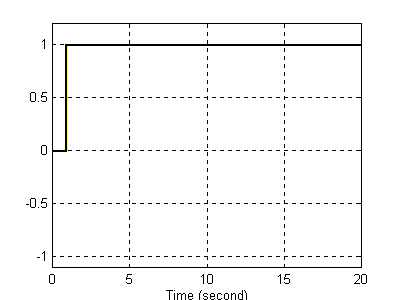
Jak widać przebieg sygnału wyjściowego wskazuje na to , że badany człon realizuje operację różniczkowania rzeczywistego. I ponownie otrzymujemy ciągły wykres, mimo iż powinien on składać się tylko z punktów odpowiadającym poszczególnym podziałkom na skali czasu.

Schemat blokowy układu nr 3

Skokiem jednostkowym podziałaliśmy na blok o transmitancji równej

Poniżej przedstawiono sygnał wejściowy oraz odpowiedź układu.

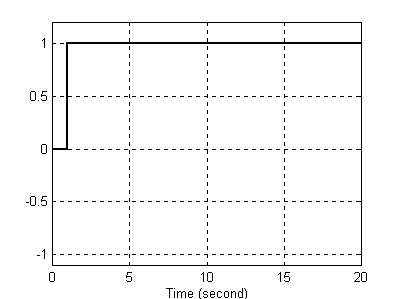
Sygnał wejściowy Sygnał wyjściowy

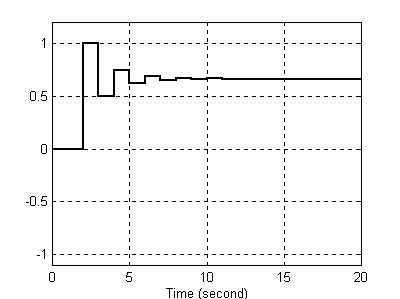
Analizując pierwiastki równania charakterystycznego transmitancji tego układu dochodzimy do wniosku, iż nasz wykres jest poprawny, gdyż układ będzie dążył do pewnego stanu ustalonego (identycznie jak na wykresie). Ponieważ pierwiastek równania charakterystycznego jest rzeczywisty i ujemny , nasz układ jest stabilny (posiada stan ustalony).

Schemat blokowy układu nr 4

Do generatora fali prostokątnej (pulse genarator) podłączony został człon realizujący całkowanie dyskretne.

Poniżej przedstawiono sygnał wejściowy oraz odpowiedź układu.

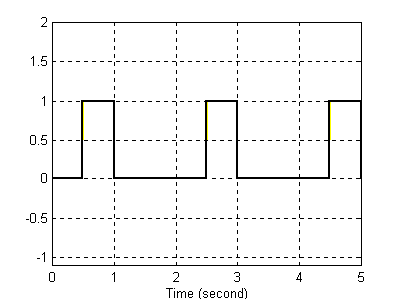
Sygnał wejściowy Sygnał wyjściowy

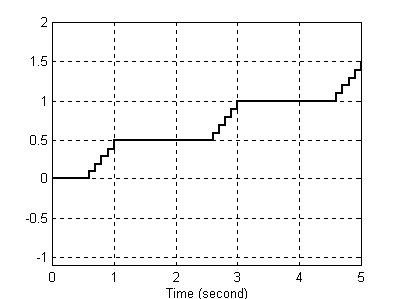
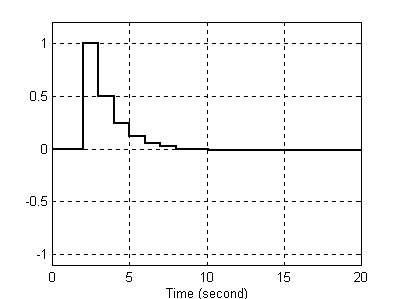
Dla takiej stałej próbkowania (T=0.1) całkowanie odbywa się zgodnie z oczekiwaniami, proces ten ulega jednak zaburzeniu, jeżeli ją zwiększamy dość radykalnie. Jest to spowodowane głównie tym, że program odczytuje tylko określone wartości w dużych (niestety) odstępach czasowych. Poniżej wykres dla T=0.8 i T=1.

Dla T=0.8

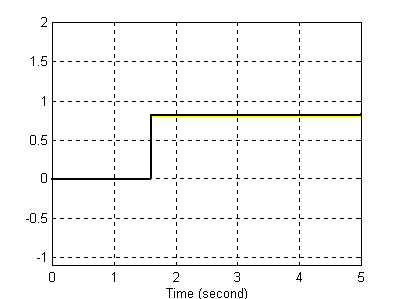
Sygnał wejściowy Sygnał wyjściowy

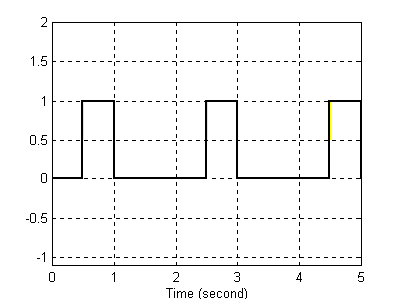
Graph Graph1

Dla T=1

Sygnał wejściowy Sygnał wyjściowy

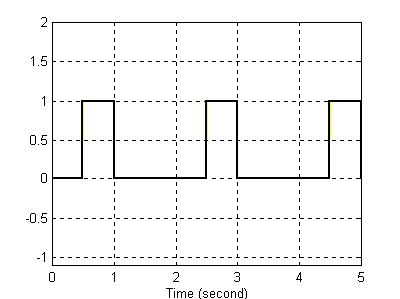
Na podstawie wykresów zauważyć można, że układ realizuje operacje całkowania. Można stwierdzić również, że im mniejsza jest wartość w liczniku, tym dokładniejsze jest całkowanie. Z kolei im licznik jest większy tym „schodki” sygnału wyjściowego są większe, i całkowanie staje się coraz mniej dokładne.

Wnioski :

Moduł matlaba - simulink jest bardzo użytecznym narzędziem, umożliwiającym w bardzo prosty i przejrzysty sposób dokonywanie symulacji dowolnych układów blokowych. Przedstawione powyżej układy i ich odpowiedzi czasowe na zadane sygnały wymuszające zostały uzyskane w tym programie. Transformata z ułatwia dosyć znacznie badanie i poznawanie własności układów impulsowych. W przypadku pierwszego układu z członem opóźniającym o transmitancji G(z) = 1/z, opóźnianie uzyskuje się dzięki temu, że sample time tego członu jest równe 1. W przypadku większych wartości człon „nie widziałby” wszystkich impulsów doprowadzonych do niego z generatora. W układzie numer trzecim mamy do czynienia z oscylującym sygnałem wyjściowym. Gdy wartość bieguna transmitancji bloku transfer fcn jest większa od -1, a mniejsza od 0, to układ można uważać za stabilny (sygnał oscylujący tłumiony), natomiast dla wartości mniejszych od -1, sygnał wyjściowy jest sygnałem oscylacyjnym nietłumionym. Układ jest wówczas układem niestabilnym. We wszystkich przypadkach dokładność układu zależy w znaczący sposób od wartości parametru sample time, który jest okresem próbkowania. Im wartość ta była mniejsza, tym odpowiedź układu była bardziej zbliżona do odpowiedzi linearnej, a układ dokładniejszy.

AGH, Wydział EAIiE Katedra Automatyki Napędu i Urządzeń Przemysłowych				Nazwisko i Imię: Marcin Szybowski
LABORATORIUM TEORII SEROWANIA I TECHNIK REGULACJI				Semestr: IV
Rok szkolny: 2001/2002		Rok studiów: II		Grupa: 8.2
Kierunek: Elektrotechnika				Nr ćwiczenia: 8
Temat ćwiczenia: Badanie dynamiki układu ciągłego z regulatorem cyfrowym
Data wykonania: 28-04-2002	Data oddania: 6-05-2002		Data zaliczenia sprawozdania:

Badanie dynamiki zamkniętego układu z ujemnym sprzężeniem zwrotnym z obiektem ciągłym oraz z regulatorem cyfrowym przeprowadzono na podstawie układu przedstawionego na poniżej zawartym rysunku:

1. Schemat blokowy

W którym obiekt ciągły o transmitancji
ma charakter całkująco-inercyjny. Natomiast ekstrapolator `0' o transmitancji
ma charakter całkujący. Człon
pełni funkcję opóźnienia, w którym T_i = 1.

W celu wyznaczenia transmitancji regulatora cyfrowego, dokonano szeregowego połączenia transmitancji obiektu ciągłego G(s) i transmitancji ekstrapolatora `0' H(s), otrzymując nową transmitancje zastępczą G_Z(s).

Następnie sprowadzono transmitancję G_Z(s) do postaci czasowej, rozkładając ją na ułamki proste, a następnie wyznaczając oryginał funkcji operatorowej:

Oryginał transmitancji operatorowej ma postać:

W kolejnym kroku przetransponowano powyższą transmitancję, korzystając z przekształcenia „z” i otrzymano transmitancję G_o(z) w postaci:

Po kolejnych przekształceniach otrzymujemy:

Po dokonaniu połączenia transmitancji obiektu ciągłego G(s) i ekstrapolatora `0' H(s), a następnie po ich przetransponowaniu za pomocą przekształcenia „z” do postaci dyskretnej G₀(z) badany układ przybiera postać:

Na podstawie wyżej zawartego schematu i stosując reguły upraszczania schematów blokowych, otrzymano wyrażenie pozwalające wyznaczyć transmitancję zastępczą układu:

Zakładając, że
oraz

Transmitancja zastępcza układu przybiera wówczas postać:

Transmitancja układu musi spełniać określone warunki:

Po pierwsze musi być skończony czas regulacji, a nastąpi to wówczas, gdy mianownik osiągnie z^k, gdzie k jest rzędem obiektu. W naszym przypadku k = 2, zatem wtedy gdy mianownik przyjmie postać z². Wtedy transmitancja zastępcza wygląda następująco:

Drugim warunkiem jest zerowy uchyb regulacji.

Wówczas możemy mówić o transmitancji uchybowej:

Podstawiając do powyższego równania G_Z(z) wynikające z pierwszego warunku otrzymujemy parametry K,
oraz
.

Szukane parametry wynoszą:

a₁ = 1

a₀ = 0,4585

K = 2,5411

Ostatecznie możemy zapisać transmitancję zastępczą badanego układu:

Korzystając z powyżej zawartej transmitancji zastępczej układu, oraz ze schematu przedstawiającego obiekt w formie dyskretnej wyznaczono transmitancję regulatora.

Po wstawieniu G_Z(z) i G₀(z) otrzymano:

Mając wyznaczoną transmitancję regulatora oraz transmitancję obiektu przeprowadzono symulację układu przy pomocy modułu matlaba simulinka na podstawie poniżej przedstawionego schematu blokowego.

Wymuszając układ skokiem jednostkowym na grafach obserwowano charakterystyki wejściową oraz wyjściową, które przedstawione są poniżej:

Charakterystyka wejściowa układu zamkniętego z obiektem ciągłym i regulatorem cyfrowym

Charakterystyka wyjściowa układu zamkniętego z obiektem ciągłym i regulatorem cyfrowym

Wnioski :

Jak widać na charakterystyce odpowiedzi układu na wymuszenie skokiem jednostkowym regulator powoduje szybkie ustalenie się przebiegu wyjściowego (poprawia w układzie dynamikę, zmniejsza stałą czasową). Układ ma przebieg ustalony już po 2 sekundach. Nie występują przeregulowania podczas ustalania się. Można by powiedzieć, że regulatory znakomicie nadają się do pracy z układami, które wymagają szybkiego ustalenia ponieważ dzięki niemu niepożądane zmiany sygnału nie spowodują uszkodzenia układu lub zaburzeń w jakimś procesie technologicznym co mogłoby spowodować szkody i grozić wypadkiem.

G(s)

RC

H(s)

_

X_Z(t)

Y(t)

ε

Regulator

cyfrowy

Dyskretyzacja

czasu

Ekstrapolator

Obiekt

---