AGH, Wydział EAIiE
|
Nazwisko i Imię: Wojciech Hanuszkiewicz |
||||
LABORATORIUM TEORII SEROWANIA I TECHNIK REGULACJI
|
Semestr: IV |
||||
Rok szkolny: 2006/2007
|
Rok studiów: II |
Grupa: 3.1 poniedziałek 12.30 |
|||
Kierunek: Elektrotechnika
|
Nr ćwiczenia: 1 i 2 |
||||
Temat ćwiczenia: Analiza podstawowych układów dyskretnych
|
|||||
Data wykonania: 12,26.03.2007 |
Data zaliczenia sprawozdania: |
Ocena:
|
|||
Analiza podstawowych układów dyskretnych.
Wiadomości wstępne
Układy dyskretne opisuje się najczęściej wykorzystując metodę przekształceń dyskretnych. Metoda ta jest swego rodzaju odpowiednikiem przekształcenia Laplace'a znajdującego szerokie zastosowanie wśród układów ciągłych. Analiza układów dyskretnych polega na dyskretyzowaniu czasu t dla t= nT(n=1,2,3,...).
Cel ćwiczenia
Na zajęciach laboratoryjnych w pracowni komputerowej obserwowaliśmy odpowiedzi odpowiednich członów dyskretnych na poszczególne sygnały wymuszające(standardowe). Calem ćwiczenia była ocena charakteru odpowiedzi na wymuszenia i wpływu zmian odpowiednich transmitancji układu na dynamikę działania konkretnych członów. Rozpatrywaliśmy odpowiedzi następujących członów dyskretnych:
- opóźniającego(unit delay)
- opisanego dyskretną transmitancją czynnikową(zera, bieguny)
- discrete transfer fnc
- członu całkującego(discrete-time integrator)
- dyskretnego układu całkującego
Badania symulacyjne przeprowadzane były w oparciu o schemat blokowy.
Przebieg ćwiczenia.
3.1 Badanie zachowania się członu opóźniającego o transmitancji dyskretnej.
![]()
Schemat blokowy programu MATLAB Simulink na podstawie którego dokonywaliśmy analizy członu opóźniającego.
schemat blokowy członu opóźniającego
Wyniki symulacji można zostały zamieszczone na dołączonych rysunkach 1 i 2
3.2 Badanie członu opisanego dyskretną transmitancja czynnikową
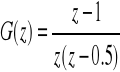
Schemat blokowy programu MATLAB Simulink na podstawie którego dokonywaliśmy analizy członu opisanego dyskretną transmitancja czynnikową
Schemat blokowy członu opisanego dyskretną transmitancja czynnikową
Jak można zaobserwować na załączonych rysunkach 3 i 4 badany człon po zadaniu na wejście skoku jednostkowego odpowiada na wyjściu przebiegiem opóźnionym którego wartość jest równa amplitudzie wymuszenia jednakże jest to przebieg zanikający skokowo do zera .
3.3 Badanie odpowiedzi członu dyskretnego Discrete Transfer Fnc na wymuszenie skokiem jednostkowym
![]()
Schemat blokowy programu MATLAB Simulink na podstawie którego dokonywaliśmy analizy odpowiedzi członu dyskretnego Discrete Transfer Fnc na wymuszenie skokiem jednostkowym
Schemat blokowy układu z członem opisanym dyskretna transmitancją
Na załączonych rysunkach 5 i 6 można zaobserwować odpowiedź członu Discrete Transfer Fnc na skok jednostkowy. Odpowiedź tego członu jest opóźniona względem sygnału wymuszającego. Wartość maksymalna odpowiedzi jest równa wartości wymuszającej przy czym badany przez nas człon wykazuje charakter oscylacyjny gdyż obserwujemy na wyjćiu oscylacje tłumione. Układ końcowo ustala pracę na wartości sygnału wymuszającego.
Badanie działania dyskretnego członu całkującego Discrete-Time Integrator
![]()
Schemat blokowy programu MATLAB Simulink na podstawie którego dokonywaliśmy analizy odpowiedzi dyskretnego członu całkującego
Schemat blokowy układu z dyskretnym członem całkującym
Na zamieszczonych rysunkach 7, 8, 9 można zaobserwować wyniki przeprowadzonych symulacji. Rys 7 przedstawia przebieg wejściowy natomiast rys 8 i 9 przebiegi wyjściowe(8 dla T=1; 9 dla T= 0.3). Prostokątny przebieg wejściowy badanego członu generuje narastający przebieg dążący do wartości ustalonej .
Badanie działania dyskretnego układu filtrującego.
Schemat blokowy programu MATLAB Simulink na podstawie którego dokonywaliśmy analizy odpowiedzi dyskretnego układu filtrującego
![]()
Schemat blokowy układu analizy dyskretnego układu filtrującego
Na rys 10-12 przedstawiono wyniki symulacji(rys 10-wejście, 11,12 wyjście gdzie 11 otrzymano dla okresu równego 1, natomiast 12 otrzymano dla współczynnika przy z równemu 1 i zadanemu okresowi równemu 1).
Układ ciągły z regulatorem dyskretnym.
1. Wiadomości wstępne, cel ćwiczenia.
Opisy liniowych układów ciągłych uzyskuje się dzięki transmitancji, która stanowi stosunek sygnału wyjścia do sygnału wejścia w dziedzinie Laplace'a. Podobnie rzecz ma się w przypadku opisów układów zawierających co najmniej jeden impulsator, w takim przypadku stosuje się tzw. transmitancję dyskretną.
Podczas zajęć laboratoryjnych w pracowni komputerowej wykorzystując program MATLAB i jego zakładkę Simulink dokonywaliśmy obserwacji działania regulatora cyfrowego.
2. Przebieg ćwiczenia
Podczas ćwiczenia laboratoryjnego dokonywaliśmy doboru regulatora cyfrowego. W tym celu oparliśmy się na następujących kryteriach:
- Zapewnienie minimum czasu regulacji
![]()
- zerowego uchybu regulacji
![]()
W programie Simulink za pomocą odpowiednich bloków utworzyliśmy schemat blokowy regulatora cyfrowego, następnie w oparciu o schemat należało wyznaczyć transmitancję układu zamkniętego.
![]()
gdzie ![]()
-transmitancja dyskretna regulatora cyfrowego.
Jeżeli oznaczymy:
![]()
![]()
to transmitancja układu zamkniętego wynosi
![]()
Minimalny i skończony czas regulacji zapewnia zależność:
![]()
gdzie k -jest rzędem obiektu.
Następnym krokiem jest określenie transmitancji uchybowej:
![]()
dla przekształcenia z obowiązuje relacja:
![]()
gdzie E(z)- uchyb dyskretny
![]()
Wyrażenie ![]()
jest transformatą(z) skoku jednostkowego.
Odchyłka ustalona
![]()
Warunek ten jest spełniony gdy transmitancja ![]()
zawiera w liczniku czynnik (z-1).
![]()
![]()
Wstawiamy tę zależność do poprzedniego równania i przez porównanie wyznaczymy współczynniki ![]()
![]()
K
![]()
=1, ![]()
=0,4585, K=2,5411
Znając postać ![]()
można określić transmitancję dyskretną regulatora ![]()
![]()
3. przebieg ćwiczenia laboratoryjnego
Podczas zajęć zajęć przeprowadziliśmy obliczenia tablicowe umożliwiające przedstawienia poszukiwanych przez nas obliczeń przejściowych. Następnie w programie MATLAB napisaliśmy program dzięki któremu mogliśmy sprawdzić recznie obliczone wartości. Otrzymane dane były niezbędne do dalszego prowadzenia symulacji.
Schemat blokowy programu MATLAB Simulink na podstawie którego dokonywaliśmy analizy odpowiedzi układu ciągłego z regulatorem cyfrowym
Schemat blokowy układu z dobranym regulatorem cyfrowym
Na dołączonych rysunkach 13-15 można zauważyć dojście układu do wartości ustalonej po pewnym czasie i skokowo.
Wyszukiwarka
Podobne podstrony:
LAB11 Analiza podstawowych uk?ów dyskretnych
Analiza podstawowych uk adów dyskretnych vel Hamas, Elektrotechnika AGH, Semestr IV letni 2013-2014,
Generatory drgan sinusoidalnych1, Celem ˙wiczenia jest zapoznanie si˙ z wybranymi podstawowymi uk˙ad
01'''', WZMACNIACZ RC jest on podstawowym uk˙adem wzmacniacza W wersji tranzystorowej to wzmacniacz
uk-ad krwionoÂny. aq, Biomedyczne podstawy rozwoju i wychowania
Uk-ad pokarmowy cz-owieka. aq, Biomedyczne podstawy rozwoju i wychowania
Dyskretny nieliniowy ukŕad semidynamiczny na pŕaszczyŻnie
Uk-ad oddechowy. aq, Biomedyczne podstawy rozwoju i wychowania
Analiza ukŕadˇw detekcji ze stabilizacjĐ poziomu faŕszywego alarmu
uk-ad krwionoÂny. aq, Biomedyczne podstawy rozwoju i wychowania
WICZENIE 1 Biologia cz owieka uk ad kostny podstawy
uk ad pokarmowy
Wykład II Analiza podstawowych pojęć eksploatacyjnych i użytkowanie obiektów ED
UK AD LIMFATYCZNY, rodzaje i zasady masażu
arkusz analizy podstawy pr
uk+éad kr¦ů+ enia
PRZEGR 1, Sprawdzi˙ pod wzgl˙dem cieplno-wilgotno˙ciowym przegrod˙ budowlan˙ pionow˙ o nast˙puj˙cym
TEATR OPRACOWANIA I sem, Raszewski- Uk+éad S, Raszewski - układ S
więcej podobnych podstron