
Politechnika Warszawska
Wydział Elektroniki i Technik Informacyjnych
Instytut Systemów Elektronicznych
PRACA MAGISTERSKA
Analiza układów detekcji ze stabilizacją poziomu
fałszywego alarmu
Autor:
Igor Kulkowski
Kierownik pracy:
dr inż. Krzysztof Kulpa
Warszawa 2000

2
SPIS TREŚCI
WSTĘP......................................................................................................................... 4
1. PODSTAWY I NAJWAŻNIEJSZE POJĘCIA TEORII DETEKCJI............................ 6
1.1. PARAMETRY OKREŚLAJĄCE JAKOŚĆ DETEKCJI ........................................ 6
1.2. POJĘCIE RYZYKA. OPTYMALNE KRYTERIA DECYZYJNE ........................... 9
1.3. PRZYKŁAD OPTYMALNEJ DETEKCJI........................................................... 14
1.4. WERYFIKACJA HIPOTEZ ZA POMOCĄ POMIARÓW WIELOKROTNYCH ... 21
1.5. PRZYKŁAD OPTYMALNEJ DETEKCJI NA PODSTAWIE WIELU POMIARÓW
........................................................................................................................ 25
2. ANALIZA UKŁADÓW OPTYMALNEJ DETEKCJI RZECZYWISTYCH SYGNAŁÓW
RADAROWYCH .................................................................................................... 30
2.1. DETEKCJA SYGNAŁU O NIEZNANYCH PARAMETRACH............................ 30
2.2. STOSUNEK WIARYGODNOŚCI DLA SYGNAŁU O NIEZNANYCH
PARAMETRACH............................................................................................. 34
2.3. STOSUNEK WIARYGODNOŚCI DLA SYGNAŁU O NIEZNANEJ FAZIE........ 36
2.4. ZASTOSOWANIE FILTRU DOPASOWANEGO W DETEKCJI SYGNAŁÓW Z
NIEZNANYM CZASEM OPÓŹNIENIA ............................................................ 40
2.5. ZASTOSOWANIE ZESPOLONYCH AMPLITUD W ANALIZIE PROCESU
DETEKCJI....................................................................................................... 42
3. INTEGRACJA IMPULSÓW I STABILIZACJA POZIOMU FAŁSZYWEGO ALARMU
.............................................................................................................................. 54
3.1. ZASADA DZIAŁANIA RZECZYWISTYCH SYSTEMÓW RADIOLOKACYJNYCH
........................................................................................................................ 54
3.2. STOSUNEK WIARYGODNOŚCI DLA SYGNAŁU W POSTACI PACZKI
IMPULSÓW W.CZ. O NIEZNANYCH FAZACH............................................... 59
3.3. DETEKTOR DLA SYGNAŁU W POSTACI PACZKI IMPULSÓW W.CZ. O
NIEZNANYCH FAZACH.................................................................................. 61
3.4. INTEGRATOR BINARNY................................................................................ 65
3.5. FAŁSZYWY ALARM........................................................................................ 66

3
4. ANALIZA JAKOŚCI UKŁADÓW OPTYMALNEJ DETEKCJI SYGNAŁÓW
RADIOLOKACYJNYCH ........................................................................................ 72
4.1. ROKŁADY OBWIEDNI SYGNAŁU .................................................................. 73
4.2. ROZKŁADY SYGNAŁU ZA UKŁADEM CFAR................................................. 80
4.3. ROZKŁADY SYGNAŁU ZA INTEGRATOREM BINARNYM ............................ 85
4.4. ROZKŁADY SYGNAŁU ZA INTEGRATOREM DZIAŁAJĄCYM
BEZPOŚREDNIO NA AMPLITUDZIE ............................................................. 90
DODATKI ................................................................................................................... 95
A: OPIS ZESTAWU FUNKCJI SŁUŻĄCYCH DO ANALIZY DETEKTORÓW
CYFROWYCH................................................................................................. 95
binint........................................................................................................... 96
dbloss......................................................................................................... 98
detect ....................................................................................................... 100
normaliz.................................................................................................... 102
pdftocdf .................................................................................................... 104
ricepdf ...................................................................................................... 106
sqrtpdf ...................................................................................................... 107
sumpdf ..................................................................................................... 109
B: KODY
ŹRÓDŁOWE FUNKCJI SŁUŻĄCYCH DO ANALIZY DETEKTORÓW
CYFROWYCH............................................................................................... 111
binint......................................................................................................... 111
dbloss....................................................................................................... 112
detect ....................................................................................................... 113
normaliz.................................................................................................... 114
pdftocdf .................................................................................................... 115
ricepdf ...................................................................................................... 116
sqrtpdf ...................................................................................................... 116
sumpdf ..................................................................................................... 117
PODSUMOWANIE ................................................................................................... 119
LITERATURA........................................................................................................... 120

4
WSTĘP
Minęło ponad pięćdziesiąt lat od skonstruowania pierwszego radaru. Od
tamtej chwili urządzenia te zostały bardzo unowocześnione. Obecnie operator
nie musi się już bez przerwy wpatrywać w ekran obrazujący przestrzeń dookoła
stacji czy też w przebieg sygnału echa i na ich podstawie samemu podejmować
decyzję o obecności celu. Dzięki zastosowaniu metod cyfrowej obróbki sygnału
możliwe stało się zwiększenie prawdopodobieństwa wykrycia obiektów, a co za
tym idzie, można w większości przypadków odciążyć operatora i zrzucić
podejmowanie decyzji na maszynę. Układy detekcyjne składają się z wielu
bloków odpowiednio przekształcających sygnał echa tak, aby wykrycie było
możliwe nawet w niesprzyjających warunkach. Jednak taka duża komplikacja
systemów powoduje, że na etapie projektowania ich analiza staje się bardzo
żmudna i czasochłonna
−
zwłaszcza przy stosowaniu metod analitycznych. Z
pomocą mogą tu przyjść komputery. Stosując metody numeryczne można
znacznie skrócić czas potrzebny na przebadanie układu detektora.
Głównym celem niniejszej pracy jest stworzenie narzędzi w postaci
zestawu programów, które ułatwiałyby analizę detektorów cyfrowych.
Pozwalałyby one na określenie rozkładów prawdopodobieństw sygnału echa
wraz z zakłóceniami zarówno na wyjściu anteny jak i po przejściu przez
poszczególne bloki obróbki sygnału. Czynnością końcową byłoby wykreślenie
dla konkretnego zestawu bloków funkcjonalnych charakterystyk detekcji. Celem
drugoplanowym, ale wynikającym bezpośrednio z celu głównego, jest
przeprowadzenie analizy statystycznej cyfrowych układów detekcji oraz podanie
metod pozwalających na wyznaczenie odpowiednich rozkładów
prawdopodobieństwa.

5
Niniejsza praca składa się z czterech rozdziałów, z czego trzy pierwsze
zawierają analizę teoretyczną problemu, natomiast w rozdziale czwartym
przeprowadzono analizę jakości układów detekcji, wykorzystując jako narzędzia
stworzone w ramach realizowanej pracy dyplomowej zestawy programów,
pracujące w środowisku MATLAB.
W rozdziale pierwszym podano najważniejsze pojęcia teorii wykrywania,
zaprezentowano wybrane kryteria decyzyjne oraz omówiono problem
optymalnej detekcji pojedynczych wartości oraz sygnałów całkowicie znanych.
Przytoczono także prosty przykład optymalnej detekcji.
Rozdział drugi porusza problem wykrywania sygnałów w sytuacji, gdy
część z jego parametrów jest nieznana i może zmieniać się losowo.
Przeprowadzono teoretyczne rozważania, których wynikiem jest schemat
optymalnego układu detekcji z podziałem na bloki funkcjonalne, wykonujące
różne operacje na sygnale.
W trzecim rozdziale omówiono problem stabilizacji poziomu
prawdopodobieństwa fałszywego alarmu oraz integracji wielu impulsów, czyli
podejmowania decyzji w oparciu o dużą liczbę odbieranych sygnałów. W tym
miejscu przedstawiono podstawowe typowe rozwiązania detektorów oraz
sposób ich działania.
Omówione trzy rozdziały stanowią swego rodzaju próbę
uporządkowanego i uszeregowanego opisu rozważań dotyczących problemów
detekcji sygnałów, przedstawianych w polskojęzycznej literaturze w sposób
wyrywkowy lub pobieżny.
Rozdział czwarty zawiera analizę jakości układów detekcji. W rozdziale
tym wyliczono rozkłady prawdopodobieństw sygnałów na wyjściu
poszczególnych bloków funkcjonalnych całego układu optymalnej detekcji oraz
wykreślono dla nich charakterystyki wykrywania. Na końcu pracy dyplomowej,
w dodatkach A i B, znajdują się dokładny opis do stworzonych narzędzi oraz
kod źródłowy.
Napisane funkcje, pracujące w środowisku MATLAB, pozwoliły na
numeryczne wyznaczenie rozkładów prawdopodobieństw, oraz na wykreślenie
zamieszczonych w rozdziale czwartym charakterystyk detekcji dla różnych
typów detektorów.

6
Przedstawione w pracy autorskie narzędzia do analizy całych układów
detekcji oraz ich poszczególnych bloków stanowią uwieńczenie rozważań
teoretycznych i wydaje się, że mogą być przydatne w procesie dydaktycznym, a
także w pracach naukowo-badawczych.

7
1. PODSTAWY I NAJWAŻNIEJSZE POJĘCIA
TEORII DETEKCJI
1.1. PARAMETRY OKREŚLAJĄCE JAKOŚĆ DETEKCJI
Celem radiolokacji jest uzyskanie informacji na temat obiektów latających
znajdujących się w przestrzeni powietrznej oraz ich współrzędnych. Informacje
te uzyskuje się poprzez sondowanie przestrzeni sygnałami radiowymi. Jeśli
gdzieś w powietrzu znajduje się samolot, to sygnał odbije się od niego i wróci
do stacji nadawczo-odbiorczej. Na wejściu odbiornika poza sygnałem odbitym
od rzeczywistego obiektu znajdują się także zakłócenia. Są to np. sygnały
pochodzące od innych stacji radiolokacyjnych, odbite od powierzchni wody,
gęstych chmur czy nieruchomych obiektów na ziemi. Powodują one błędy w
wykrywaniu obiektów i określaniu ich współrzędnych. Przypadkowość sygnałów
radiolokacyjnych i zakłóceń powoduje, że przy analizie działania radaru
konieczne jest zastosowanie metod statystycznych i używanie do oceny jego
jakości parametrów statystycznych.
Analiza sygnałów radiolokacyjnych docierających z przestrzeni
powietrznej powinna być zakończona podjęciem decyzji na temat obecności lub
nieobecności obiektu w określonym miejscu przeszukiwanej przez radar
przestrzeni. Decyzja może być podjęta przy spełnieniu dwóch wzajemnie
wykluczających się warunków:
warunek H
1
−
"obiekt jest"
warunek H
0
−
"obiektu nie ma".
W trakcie podejmowania decyzji nie wiadomo, który z warunków jest w
rzeczywistości spełniony. Stawiane są dwie hipotezy co do obecności celu.
Celem jest ustalenie, która jest prawdziwa, a którą należy odrzucić.
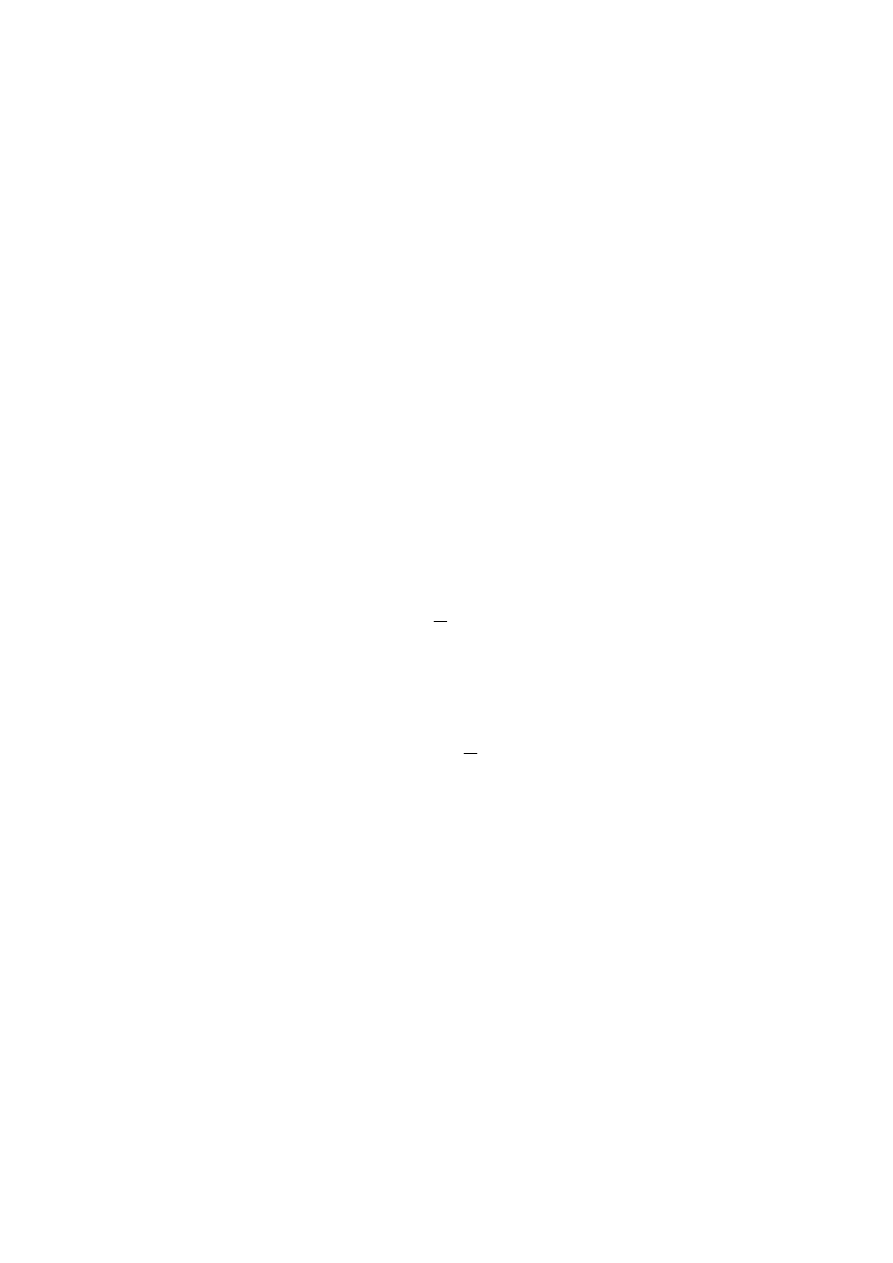
8
Każdej z powyższych hipotez można przypisać dwie różne decyzje:
decyzja d
1
−
"obiekt jest"
decyzja d
0
−
"obiektu nie ma".
Zakłada się, że po zakończeniu procesu wykrywania nie może mieć miejsca
decyzja "nie wiem".
Jeśli spełniona jest hipoteza H
1
, to znaczy gdy obiekt faktycznie znajduje
się w przestrzeni i zostanie podjęta decyzja d
1
−
"obiekt jest", to mówi się o
poprawnym wykryciu (detekcji). Jeżeli spełniona jest powyższa hipoteza, a
zostanie podjęta decyzja d
0
−
"obiektu nie ma", to mówi się o tzw. fałszywym
spokoju (ang. false dismissal)
−
obiekt w powietrzu pozostał nie zauważony.
Taki błąd zwany jest często błędem II rodzaju i jest ze wszech miar
niepożądany. Jakość detekcji przy hipotezie H
1
można określić poprzez
odpowiednie prawdopodobieństwa warunkowe:
prawdopodobieństwo poprawnego wykrycia
)
/
(
1
1
H
d
P
D
=
(1.1)
oraz prawdopodobieństwo przepuszczenia celu
)
/
(
1
0
H
d
P
D
=
(1.2)
Ponieważ decyzje d
1
i d
0
stanowią wzajemnie wykluczające się zdarzenia
losowe i związane są z tą samą hipotezą H
1
(obiekt jest), suma
prawdopodobieństw detekcji i przepuszczenia celu równa jest jedności
1
=
+
D
D
(1.3)
Znajomość warunkowego prawdopodobieństwa detekcji pozwala zawsze
określić warunkowe prawdopodobieństwo fałszywego spokoju. Jeśli np. dla
jednego cyklu wykrywania prawdopodobieństwo detekcji wynosi 0,9, to
prawdopodobieństwo przepuszczenia celu wynosi 0,1. Oznacza to, że radar
gwarantuje wykrycie obiektu średnio w 90% przypadków, natomiast w 10
przypadkach na 100 obiekt pozostanie nie zauważony.
Jeśli spełniona jest hipoteza H
0
, to znaczy gdy obiektu nie ma w
obserwowanej przestrzeni, poprawną jest decyzja d
0
−
"obiektu nie ma". Jeżeli z
powodu zakłóceń sygnał odebrany zostanie źle zinterpretowany i podejmie się
decyzję d
1
−
"obiekt jest", mówi się o tzw. fałszywym alarmie (ang. false alarm).
Fałszywy alarm określany jest często jako błąd I rodzaju i także jest bardzo
niepożądany. Nie jest tak groźny jak np. niewykrycie wrogiego samolotu, ale

9
błędne informacje mogą obciążać zbędnie system obróbki danych. Może to
doprowadzić do zakłóceń w przekazywaniu i analizie danych prawidłowych.
Jakość wykrywania obiektu przy jego nieobecności w przestrzeni (spełnieniu
hipotezy H
0
) także określa się przez prawdopodobieństwa warunkowe:
prawdopodobieństwo fałszywego alarmu
)
/
(
0
1
H
d
P
F
=
(1.4)
oraz prawdopodobieństwo poprawnego niewykrycia
)
/
(
0
0
H
d
P
F
=
(1.5)
Ponieważ decyzje d
1
i d
0
wzajemnie się wykluczają i odpowiadają tej samej
hipotezie H
0
(obiektu nie ma), zachodzi podobnie jak dla prawdopodobieństw
detekcji i przepuszczenia celu:
1
=
+
F
F
(1.6)
Znajomość prawdopodobieństwa fałszywego alarmu F pozwala zawsze
określić prawdopodobieństwo poprawnego niewykrycia.
Jeżeli radar obserwuje pewien fragment przestrzeni i np. F=10
-6
, to
oznacza iż na 10
6
sondowań tego fragmentu pojawi się średnio jeden fałszywy
alarm, a 999999 przypadkach poprawnie da informację, że ten obszar
przestrzeni jest pusty. Stacja radarowa przeszukuje z reguły w jednostce czasu
cały obszar powietrzny wokół siebie
−
dużą liczbę nie pokrywających się małych
fragmentów przestrzeni. Jeśli mamy n fragmentów i dla pojedynczego
n
F
1
<<
to dla całej przestrzeni prawdopodobieństwo fałszywego alarmu F
n
rośnie
proporcjonalnie do n. Prawdopodobieństwo poprawnego niewykrycia
n
n
F
F
)
(
=
stąd
nF
nF
F
F
n
n
=
−
−
≈
−
−
=
)
1
(
1
)
1
(
1
(1.7)
Ten powyższy fakt powoduje, że w teorii detekcji sygnałów radarowych
przyjmuje się typowo bardzo małe dopuszczalne prawdopodobieństwo
fałszywego alarmu dla pojedynczego fragmentu przestrzeni.
n
F
F
ndop
dop
=

10
Natomiast wartość prawdopodobieństwa detekcji D powinna być jak
największa. Są to warunki trudne do zrealizowania, zwłaszcza gdy obiekt
znajduje się w dużej odległości od radaru i energia sygnału odbitego od celu
jest niska. Granice strefy wykrywania radaru określa się odległością, na której w
jednym cyklu obserwacji prawdopodobieństwo detekcji D nie jest mniejsze od
założonej wartości dopuszczalnej D
dop
.
Tak więc głównymi parametrami określającymi jakość detektora w
systemach radarowych są prawdopodobieństwa warunkowe detekcji D oraz
fałszywego alarmu F. W granicach strefy wykrywania musi być spełnione:
F<F
dop
oraz D
≥
D
dop
.
1.2. POJĘCIE RYZYKA. OPTYMALNE KRYTERIA DECYZYJNE
Wymagania stawiane radarom tzn. jak najmniejsze F oraz jak największe
D są często sprzeczne. Aby uniknąć przepuszczenia celu, a w konsekwencji
tego np. ataku, wskazane jest podejmowanie decyzji "obiekt jest" w przypadku,
gdy odebrany sygnał jest mocno zakłócony i zniekształcony i trudno z
pewnością stwierdzić, że gdzieś w przestrzeni jest samolot. Takie postępowanie
prowadzi do wzrostu częstości występowania fałszywego alarmu. Zachodzi
więc konieczność znalezienia kompromisu między tymi sprzecznymi
wymaganiami. Trzeba znaleźć taką metodę obróbki danych radiolokacyjnych,
aby była ona optymalna z punktu widzenia całego procesu analizy. Uzyskany
tak sposób podejmowania decyzji o obecności lub nieobecności celu może
okazać się w pewnych konkretnych sytuacjach nie najlepszy. Powinien być
jednak optymalny w sensie statystycznym tzn. uwzględniać rozkłady
prawdopodobieństwa możliwych sytuacji w procesie wykrywania.
Przy poszukiwaniu optymalnych rozwiązań dla tego rodzaju problemów
zasadne jest posługiwanie się pojęciem ryzyka [10]. Można się nim z
powodzeniem posługiwać w innych dziedzinach nie związanych z systemami
radarowymi np. w telekomunikacji czy w gospodarce
−
wszędzie tam, gdzie
trzeba podjąć jedną z wielu możliwych do wyboru decyzji. W radiolokacji

11
pozwala ono na jednolite i dostatecznie ogólne potraktowanie problemu detekcji
sygnałów radiolokacyjnych oraz estymacji ich parametrów.
Do zbioru możliwych sytuacji podczas wykrywania obiektów zaliczane są
wszystkie możliwe stany wynikające w procesie radiolokacji oraz
przyporządkowane im decyzje. Mogą wystąpić a priori cztery poniższe sytuacje:
1.
d
0
H
0
−
poprawne niewykrycie obiektu
2.
d
1
H
0
−
fałszywy alarm
3.
d
0
H
1
−
fałszywy spokój
4.
d
1
H
1
−
poprawne wykrycie obiektu.
Analogicznie wygląda to w przypadku estymacji jakiejś wielkości zmieniającej
się w sposób ciągły. Przykładowo każdy pomiar odległości obiektu od radaru
polega na tym, że estymowanemu parametrowi
α
H
przypisuje się różniącą się
od niego estymatę (inaczej podejmuje się decyzję odnośnie wartości
parametru)
α
d
. W wyniku tego powstaje błąd estymacji
ε
=
α
d
-
α
H
. Zbiór
możliwych sytuacji składa się ze wszystkich możliwych par
α
d
i
α
H
.
Każdej z możliwych sytuacji odpowiada określone prawdopodobieństwo.
W przypadku detekcji można mówić o prawdopodobieństwach P
i
i-tej sytuacji
(i=1,2,3,4), których suma równa jest jedności:
1
)
,
(
)
,
(
)
,
(
)
,
(
1
1
1
0
0
1
0
0
4
3
2
1
=
+
+
+
=
+
+
+
H
d
P
H
d
P
H
d
P
H
d
P
P
P
P
P
(1.8)
W przypadku estymacji parametrów sytuacje (
α
d
,
α
H
) opisywane są
dwuwymiarową gęstością prawdopodobieństwa p(
α
d
,
α
H
). Analogicznie, jak dla
detekcji suma prawdopodobieństw wszystkich możliwych sytuacji równa jest
jedności:
∫ ∫
∫
∞
∞
−
∞
∞
−
=
=
)
,
(
1
)
(
)
(
H
d
H
d
H
d
H
d
dP
d
d
p
α
α
α
α
α
α
α
α
Każdej możliwej sytuacji można także przyporządkować pewną liczbę
mającą sens kosztu (straty) związanego z popełnionym błędem. Wielkość straty
zależy od ważności popełnionego błędu tzn. większemu błędowi
przyporządkowywana jest z reguły większa strata. Zwykle przyjmuje się, że
koszt bezbłędnych decyzji jest równy zeru. Przyporządkowywanie
poszczególnym błędom odpowiednich strat stanowi istotny etap w ogólnej
analizie danego problemu. Dlatego powinno się uwzględnić w nim wszelkie
dane o tym, na ile niepożądany jest jakiś rodzaj błędu. Strata może być

12
określona np. przez przesłanki typu ekonomicznego, czy strategicznego.
Trzeba by się np. zastanowić, co mogłoby być gorsze i więcej kosztować:
fałszywy alarm i poderwanie samolotów w celu przechwycenia widma, czy
przepuszczenie wrogiego samolotu i narażenie na atak z powietrza. Metody
znajdowania straty nie należą do teorii związanej z wykrywaniem. W wielu
przypadkach postać optymalnej reguły obróbki sygnałów (w przypadku detekcji
tzw. reguły decyzyjnej) nie jest zależna od konkretnej postaci funkcji strat.
Strata jest określona dla każdej możliwej sytuacji w sposób niezależny od
reguły decyzyjnej. Te dwa pojęcia można jednak ze sobą powiązać i otrzymać
w ten sposób ocenę jakości reguły decyzyjnej. W przypadku, gdy stany
(hipotezy dotyczące obiektu w przestrzeni) i związane z nimi decyzje są
wielkościami przypadkowymi o ustalonych prawdopodobieństwach, jako miernik
jakości reguły decyzyjnej można przyjąć stratę uśrednioną na wszystkie stany i
wszystkie decyzje. Wprowadza się pojęcie średniej (w sensie statystycznym)
straty zwanej ryzykiem. Dla zmiennej losowej skokowej
−
którą jest zbiór
wszystkich możliwych sytuacji w procesie detekcji ryzyko liczy się następująco:
∑
=
i
i
i
P
r
r
(1.9)
gdzie:
r
i
−
strata dla i-tej sytuacji
P
i
−
prawdopodobieństwo występowania i-tej sytuacji.
Dla zmiennej losowej ciągłej (estymacja parametrów) ryzyko liczy się z
poniższego wzoru:
∫
⋅
=
)
,
(
)
(
)
(
H
d
H
d
H
d
dP
r
r
α
α
α
α
α
α
Przyglądając się procesowi detekcji widać, że błędnymi decyzjami są
sytuacje: gdy podejmie się decyzję o obecności celu, jeśli w rzeczywistości go
nie ma oraz gdy pozostawimy cel niezauważonym. Straty dla poprawnych
decyzji są równe zeru, tak więc wystarczy tylko wyznaczyć straty dla dwóch
wspomnianych wyżej błędów:
F
r
H
d
r
=
)
,
(
0
1
−
strata dla błędu fałszywego alarmu
D
r
H
d
r
=
)
,
(
1
0
−
oraz stratę dla błędu przepuszczenia celu.
Korzystając ze wzoru na prawdopodobieństwo warunkowe można zapisać, że:

13
F
H
P
H
d
P
H
P
H
d
P
⋅
=
⋅
=
)
(
)
(
)
(
)
,
(
0
0
1
0
0
1
oraz
D
H
P
H
d
P
H
P
H
d
P
⋅
=
⋅
=
)
(
)
(
)
(
)
,
(
1
1
0
1
1
0
gdzie P(H
0
) oraz P(H
1
) są prawdopodobieństwami bezwarunkowymi a priori
stanów H
0
i H
1
tzn. nieobecności lub obecności obiektu w przestrzeni. Jeśli (jak
wspomniano wyżej) koszty poprawnych decyzji są zerowe, to ryzyko w procesie
wykrywania ma postać:
)
(
)
(
1
0
H
P
D
r
H
P
F
r
r
D
F
⋅
⋅
+
⋅
⋅
=
(1.10)
Porównując różne systemy obrabiające dane radarowe za lepsze uznaje się te,
dla których ryzyko jest mniejsze. Pozwala to zdefiniować kryterium optymalizacji
dla detektorów nazywanym kryterium minimum ryzyka, znane także pod nazwą
kryterium Bayesa [4]. Projektując optymalny system wykrywania należy dążyć
do minimalizacji wyrażenia (1.10).
W przypadku estymacji parametrów strata związana z błędem jest funkcją
dwóch zmiennych r(
α
d
,
α
H
). Jeżeli np. przy estymacji odległości założyć, że
koszt zależy tylko od różnicy faktycznej odległości i jej estymaty
ε
=
α
d
-
α
H
, to
otrzymuje się funkcję jednej zmiennej r(
ε
). Jeżeli strata równa jest kwadratowi
błędu tzn.
2
2
)
(
)
(
ε
α
α
ε
=
−
=
H
d
r
to
2
2
śrkw
r
ε
ε =
=
czyli ryzyko równe jest błędowi średniokwadratowemu, a minimum ryzyka
minimum błędu średniokwadratowego.
Kryterium minimum ryzyka jest kryterium bardzo ogólnym i łatwo jest (np.
zmieniając straty) przechodzić od niego do bardziej szczegółowych i prostszych
kryteriów. Jeśli we wzorze (1.10) wstawi się
1
=
=
D
F
r
r
to otrzyma się wyrażenie na ryzyko, które równe jest sumarycznemu
prawdopodobieństwu błędów detekcji:
)
,
(
)
,
(
)
(
)
(
1
0
0
1
1
0
H
d
P
H
d
P
H
P
D
H
P
F
r
+
=
⋅
+
⋅
=
(1.11)
Kryterium minimalizujące tak zdefiniowane ryzyko nosi nazwę kryterium
idealnego obserwatora. Jest bardziej szczegółowe od wspomnianego wcześniej

14
(ogólniejszego) kryterium minimum ryzyka, gdyż nie pozwala uwzględnić różnic
w kosztach popełnienia błędów fałszywego alarmu i przepuszczenia obiektu.
Zastąpiwszy D przez 1-D w ogólnym wyrażeniu na ryzyko można je
zapisać jak poniżej:
[
]
)
(
)
(
1
0
1
H
P
r
F
l
D
H
P
r
r
D
D
⋅
⋅
−
−
⋅
=
(1.12)
gdzie
)
(
)
(
1
0
0
H
P
r
H
P
r
l
D
F
⋅
⋅
=
Ponieważ
0
)
>
1
D
P(H
r
, kryterium minimalizacji ryzyka sprowadza się do
maksymalizacji wyrażenia
F
l
D
0
−
(1.13)
Kryterium to nosi nazwę kryterium wagowego. Sprowadza się do
maksymalizacji prawdopodobieństwa detekcji D i jednoczesnej minimalizacji
prawdopodobieństwa fałszywego alarmu F. Współczynnik
0
l
pełni rolę
współczynnika wagowego. Na jego wartość wpływają zależności między
kosztami poszczególnych błędów oraz prawdopodobieństw obecności lub
nieobecności celu w pewnym fragmencie przestrzeni.
Porównując dwa detektory, z których jeden jest optymalny w sensie
kryterium wagowego można zapisać, że:
F
l
D
F
l
D
opt
opt
0
0
−
≥
−
Stąd:
)
(
0
F
F
l
D
D
opt
opt
−
⋅
+
≥
to znaczy, że dla F=F
opt
D
D
opt
≥
Gdy F
≤
F
opt
, można zapisać inaczej, że
D
D
opt
≤
Oznacza to, że optymalny detektor daje najmniejsze prawdopodobieństwo
przepuszczenia celu (czyli największe prawdopodobieństwo detekcji) ze
wszystkich detektorów, dla których prawdopodobieństwo fałszywego alarmu
jest nie większe niż dla urządzenia optymalnego.

15
W wielu sytuacjach nie tylko prawdopodobieństwo a priori, ale i koszty
błędnych decyzji są trudne do podania, czy nawet do zdefiniowania. Występuje
to np. w przypadku detekcji sygnałów radarowych, gdzie trudno określić koszty
nie wykrycia celu i gdzie prawdopodobieństwa a priori P(H
1
) i P(H
0
) mogą nie
mieć sensu. W przypadku, gdy hipoteza H
1
występuje skrajnie rzadko, głównym
czynnikiem w ogólnych średnich kosztach jest częstość F prób, w których jest
mylnie podjęta decyzja d
1
, co oznacza popełnienie błędu I rodzaju. W związku z
tym pewna kosztowna czynność wykonywana jest niepotrzebnie. Na przykład w
systemie obrony przeciwlotniczej połączonej z radarem fałszywy alarm może
doprowadzić do wystrzelenia drogiego pocisku atakującego nie istniejący cel. W
takiej sytuacji analizę (projektowanie detektora) rozpoczyna się od określenia
wartości prawdopodobieństwa F, na którą obserwator może sobie pozwolić, a
następnie poszukuje się takiego sposobu decydowania, aby osiągnąć tą
wartość i jednocześnie uzyskać minimum możliwego prawdopodobieństwa D
określającego błąd II rodzaju. Taki sposób podejścia do problemu określa
kryterium Neymana-Pearsona [1, 4]. W systemie radarowym odpowiada to
maksymalizacji prawdopodobieństwa detekcji dla założonego poziomu
prawdopodobieństwa fałszywego alarmu.
1.3. PRZYKŁAD OPTYMALNEJ DETEKCJI
Zasadność stosowania kryterium wagowego (ogólnie kryterium minimum
ryzyka) w procesie detekcji można przedstawić na prostym przykładzie miernika
wskazówkowego, mierzącego wartość napięcia. W swej istocie jest to zbliżone
do procesu wykrywania sygnałów radiolokacyjnych. Wskazania miernika można
określić liczbą y, która jest albo sumą napięcia x i zakłócenia n
n
x
y
+
=
albo tylko napięciem zakłócającym
n
y
=
Wielkości n, x i y nie zmieniają się podczas pomiaru. Wartość sygnału x jest
dokładnie znana. Znany jest też rozkład zmiennej losowej n. Na podstawie
zmierzonego napięcia y, należy podjąć decyzję d
1
lub d
0
odnośnie obecności
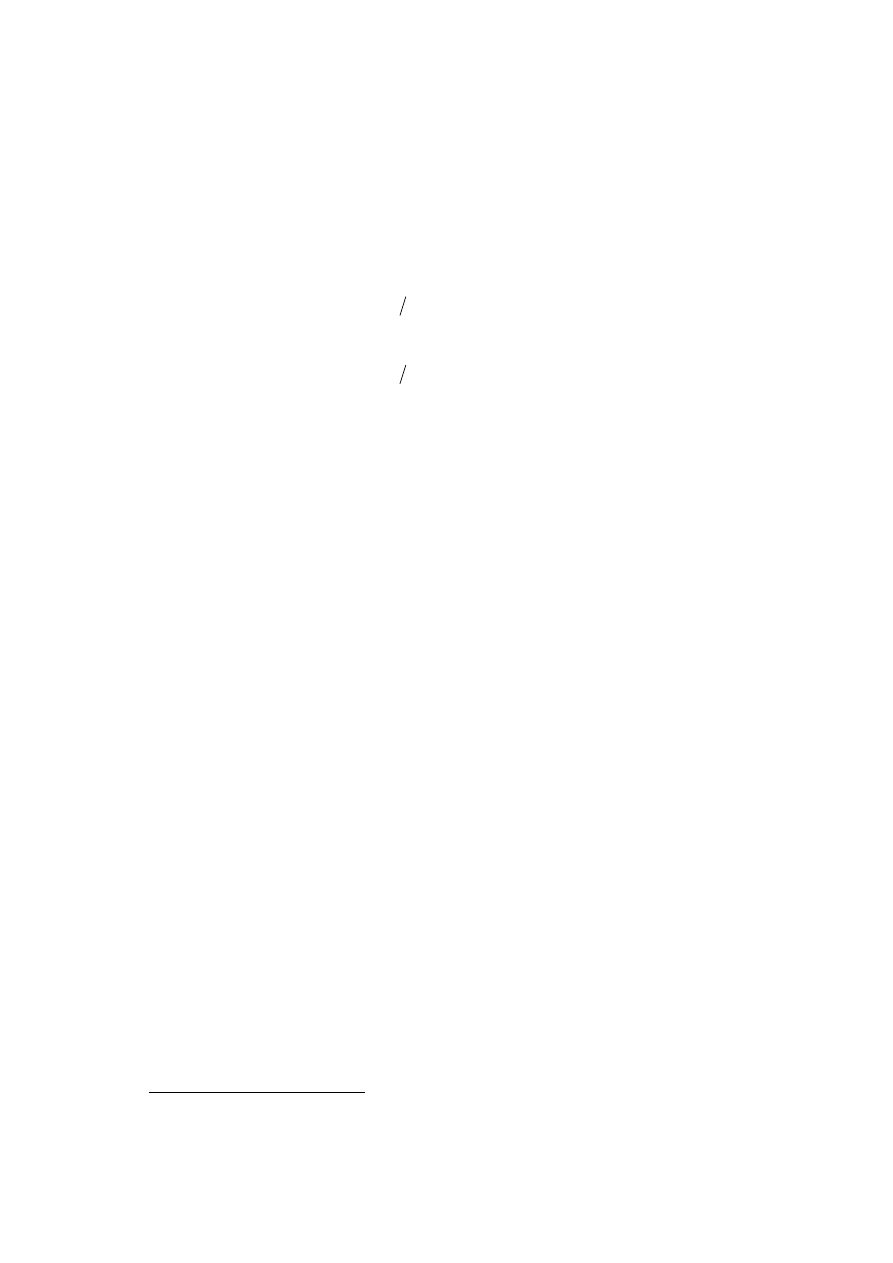
16
lub nieobecności sygnału x, która powinna być optymalna w sensie kryterium
minimum ryzyka (lub równoważnego mu kryterium wagowego).
Dla potrzeb dalszych rozważań zostanie przyjęty gaussowski rozkład
zakłóceń n. Na wykresie 1.1 na następnej stronie zostały pokazane warunkowe
gęstości prawdopodobieństw zmiennej losowej y przy nieobecności sygnału x
(warunek H
0
) i przy jego obecności (warunek H
1
)
1
:
)
(
)
(
0
y
p
H
y
p
n
=
(1.14)
)
(
)
(
1
y
p
H
y
p
n
x
+
=
(1.15)
Ponieważ rozkład zmiennej losowej n jest normalny, a x jest stałą wartością, to
krzywa p
x+n
(y) jest przesunięta względem krzywej p
n
(y) o wartość x.
)
(
)
(
x
y
p
y
p
n
n
x
−
=
+
(1.16)
Funkcja (reguła) decyzyjna rozwiązująca problem detekcji sygnału x będzie
zależeć od y i w zależności od niego przyjmować wartości 0 lub 1. Przykładowa
reguła decyzyjna d(y) (niekoniecznie optymalna) została pokazana na wykresie
1.1. W danym przypadku jeśli y
0
<y<y
1
, podejmowana jest decyzja "sygnał jest".
Dla pozostałych wartości y podejmowana jest decyzja o nieobecności sygnału
x. Prawdopodobieństwami D i F określa się prawdopodobieństwa, że sygnał y
trafi do przedziału (y
0
;y
1
)
−
odpowiednio, gdy y=x+n (sygnał i zakłócenie) oraz
gdy y=n (samo zakłócenie). Dla reguły decyzyjnej z wykresu liczone są
następująco:
∫
+
=
1
0
)
(
y
y
n
x
dy
y
p
D
(1.17)
∫
=
1
0
)
(
y
y
n
dy
y
p
F
(1.18)
1
Gdyby znane były prawdopodobieństwa a priori hipotez H
0
i H
1
tzn. P(H
0
) i P(H
1
) można by
określić ogólną funkcję gęstości prawdopodobieństwa wyników y:
)
(
)
/
(
)
(
)
/
(
)
(
1
1
0
0
H
P
H
y
p
H
P
H
y
p
y
p
⋅
+
⋅
=
17
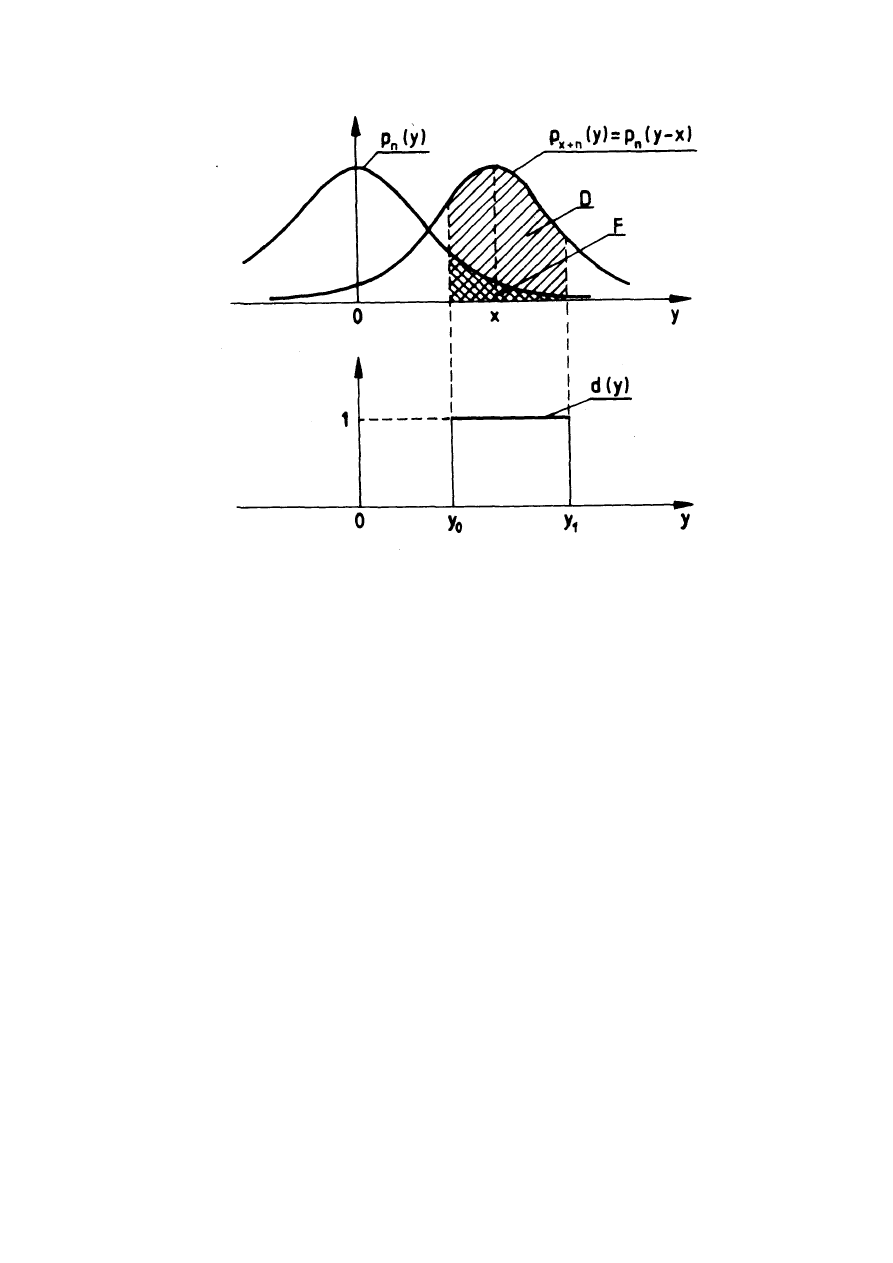
Rys. 1.1. Krzywe warunkowych rozkładów prawdopodobieństw zmiennej losowej y dla
prawdziwości hipotezy H
0
−
p
n
(y) i H
1
−
p
x+n
(y) oraz przykładowa reguła decyzyjna d(y)
Prawdopodobieństwom tym odpowiadają zakreskowane pola na pierwszym z
wykresów. Wprowadzając dowolną regułę decyzyjną do wyrażeń na D i F
można je zapisać następująco:
∫
∞
∞
−
+
⋅
=
dy
y
p
y
d
D
n
x
)
(
)
(
(1.19)
∫
∞
∞
−
⋅
=
dy
y
p
y
d
F
n
)
(
)
(
(1.20)
Na odcinkach, w których d(y)=0, obie całki będą równe zero. Natomiast tam,
gdzie d(y)=1, całki będą równe zakreskowanym na wykresie polom pod
krzywymi odpowiednio p
x+n
(y) i p
n
(y). Dwie powyższe zależności są prawdziwe
dla dowolnej postaci reguły decyzyjnej d(y).
Biorąc pod uwagę powyższe zależności, wyrażenie D-
0
l
F odpowiadające
kryterium wagowemu można przedstawić następująco:
[
]
∫
∞
∞
−
−
⋅
⋅
=
−
dy
l
y
l
y
d
y
p
F
l
D
n
0
0
)
(
)
(
)
(
(1.21)

18
gdzie
)
(
)
(
)
(
y
p
y
p
y
l
n
n
x
+
=
Zgodnie z kryterium wagowym optymalny detektor powinien
zagwarantować maksimum powyższej całki. Aby spełnić ten warunek, należy
dla każdego y maksymalizować wyrażenie podcałkowe. Można to uzyskać
przez odpowiednią modyfikację reguły decyzyjnej d(y). Funkcja d(y) przyjmuje
tylko wartości 0 lub 1, w związku z tym wyrażenie podcałkowe albo się zeruje,
albo jest mnożone przez 1. Ponieważ każda liczba dodatnia jest większa od
zera, a zero jest większe od dowolnej liczby ujemnej, łatwo jest wskazać
sposób maksymalizacji wyrażenia podcałkowego, a tym samym całego
wyrażenia: jeśli wyrażenie podcałkowe jest dodatnie przyjmuje się d(y)=1,
natomiast gdy jest mniejsze od zera zakłada się d(y)=0. Ponieważ gęstości
prawdopodobieństwa p
n
(y) i p
x+n
(y) są nieujemne, to optymalną regułę
decyzyjną dla procesu detekcji można zapisać jak niżej:
<
>
=
0
0
)
(
0
)
(
1
)
(
l
y
l
dla
l
y
l
dla
y
d
opt
(1.22)
Wielkość
)
(
)
(
)
(
y
p
y
p
y
l
n
n
x
+
=
nosi nazwę stosunku wiarygodności [1, 3, 12]. Stosunek wiarygodności jest
liczbą nieujemną i wyraża się go ilorazem gęstości prawdopodobieństw tej
samej realizacji y przy dwóch różnych warunkach: kiedy występuje sygnał i
zakłócenie oraz gdy występuje jedynie zakłócenie. Jeśli dla konkretnej wartości
y wielkość
l
(y)>
0
l
, to znaczy, że sytuacja, gdy y=x+n jest bardziej
prawdopodobna od sytuacji, gdy y=n. Ogólnie można powiedzieć, że jeśli dane
są dwa rozkłady tej samej zmiennej losowej x, z tym że pierwszy zależy od
zbioru parametrów
λ
1
, a drugi od zbioru
λ
2
i iloraz wiarygodności
)
;
(
)
;
(
2
1
λ
λ
x
p
x
p
L
=
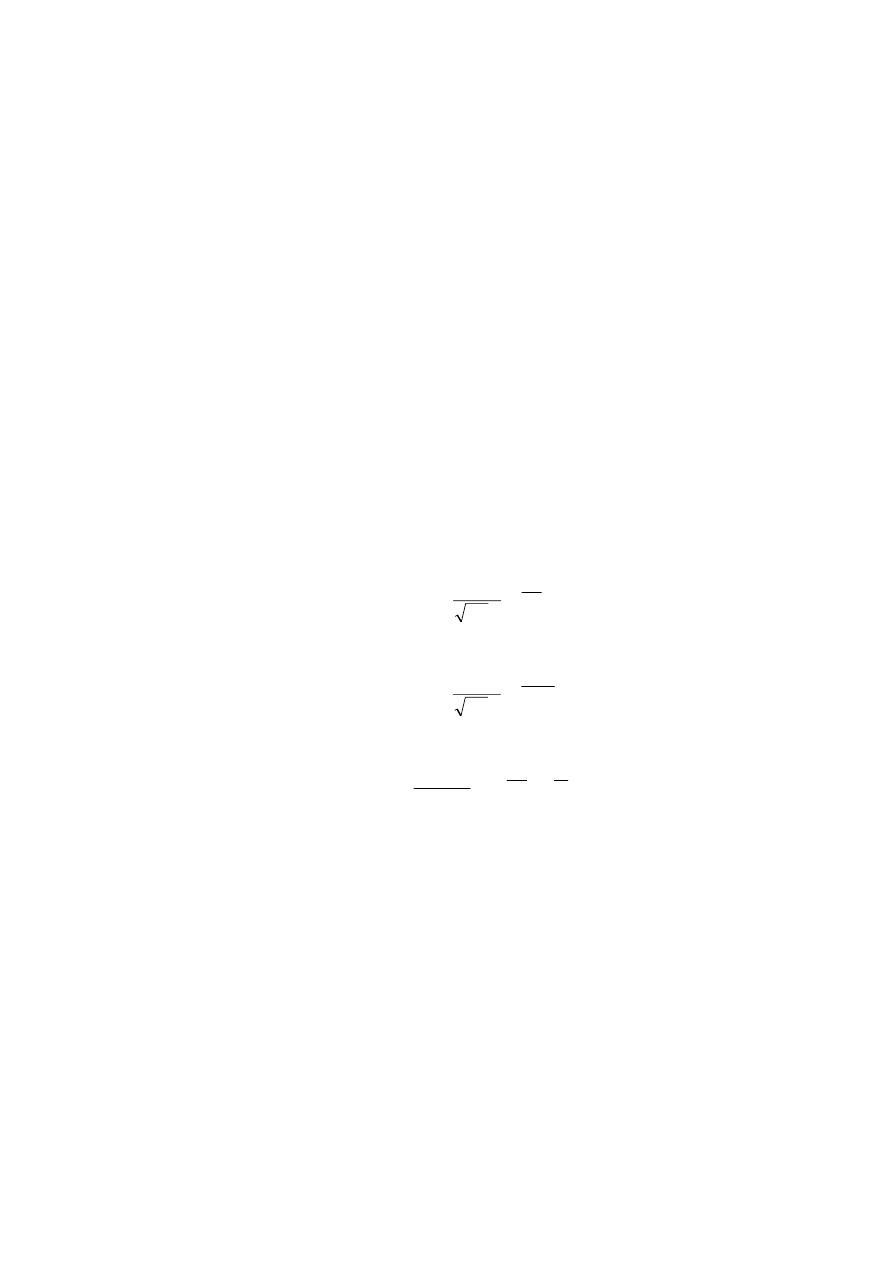
19
jest większy od założonego wcześniej progu
0
l
(w szczególnym przypadku
0
l
=1), to znaczy że zbiór parametrów
λ
1
jest bardziej prawdopodobny niż zbiór
λ
2
.
Z powyższych rozważań widać, że zamiast bardzo ogólnego kryterium
minimum ryzyka zasadniejsze jest stosowanie kryterium ilorazu wiarygodności.
Zgodnie z nim decyzję o obecności obiektu w określonym fragmencie
przestrzeni podejmuje się, gdy iloraz wiarygodności przekracza założoną
wartość progową
0
l
. Tak sformułowane kryterium optymalnego wykrywania
dobrze się nadaje do zastosowań praktycznych w systemach radarowych.
Ważne jest to, że można je stosować niezależnie od postaci rozkładu
prawdopodobieństwa zakłóceń.
W przykładzie miernika wskazówkowego przyjęto normalny rozkład
zakłóceń
)
;
0
(
σ
N
, o zerowej wartości średniej i wariancji
σ
2
. W sytuacji, gdy nie
ma sygnału użytecznego tzn. y=n, to:
e
y
n
y
p
2
2
2
2
1
)
(
σ
σ
π
−
=
W sytuacji gdy y=x+n, ponieważ p
x+n
(y)=p
n
(y-x), można zapisać:
e
x
y
n
x
y
p
2
2
2
)
(
2
1
)
(
σ
σ
π
−
−
+
=
Dla takich rozkładów iloraz wiarygodności ma postać:
e
e
xy
x
n
n
x
y
p
y
p
y
l
2
2
2
2
)
(
)
(
)
(
σ
σ
−
−
+
⋅
=
=
Przebieg krzywej
l
(y) dla x>0 pokazany jest na rysunku 1.2 na następnej
stronie (na osi rzędnych zaznaczono wartość progową
0
l
). Dzięki ścisłej
monotoniczności funkcji
l
(y), warunek
l
(y)>
0
l
można sprowadzić do warunku
y>y
0
, a
l
(y)<
0
l
odpowiednio do y<y
0
. Wcześniejsze wyrażenie na optymalną
regułę decyzyjną można zapisać jak niżej:
<
>
=
0
0
0
1
)
(
y
y
dla
y
y
dla
y
d
opt
(1.23)
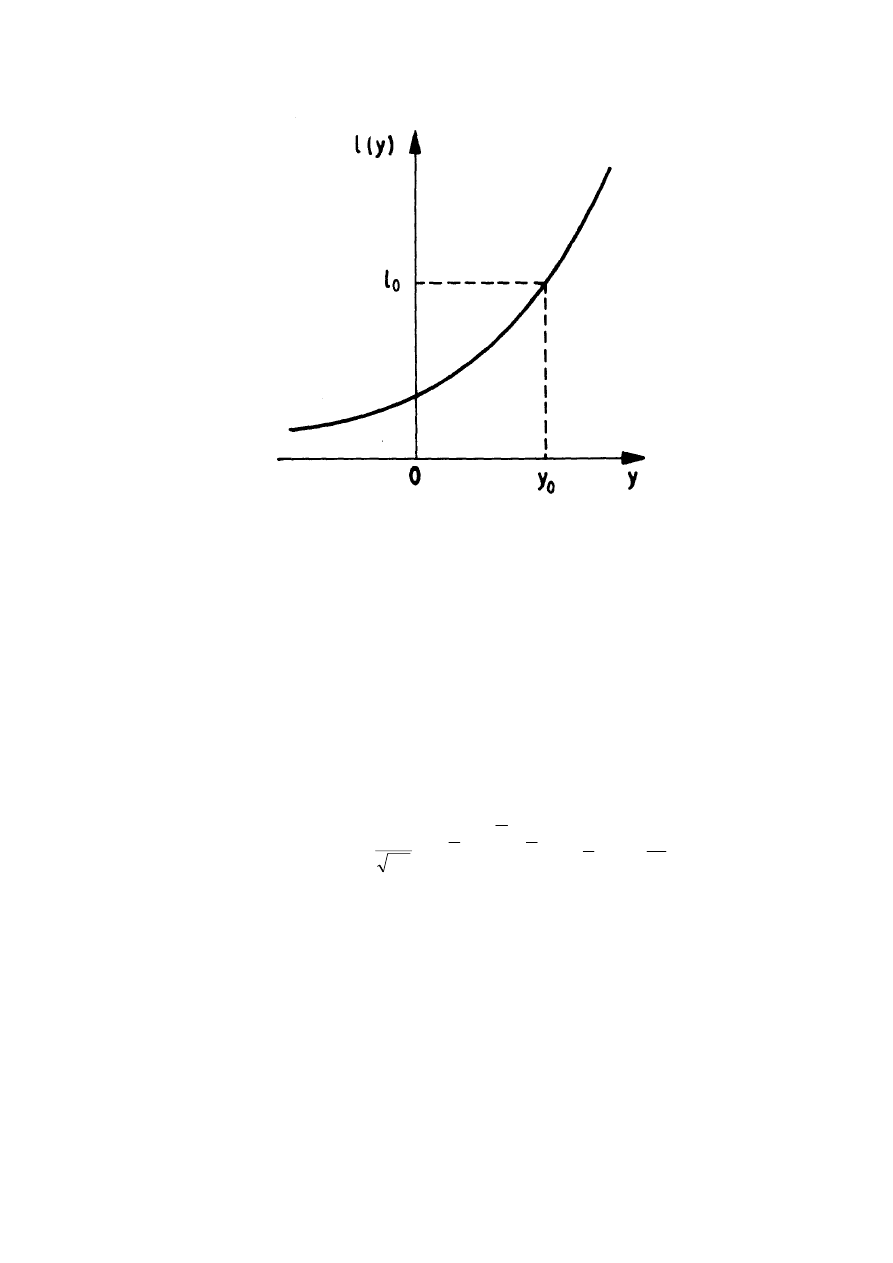
20
Rys. 1.2. Krzywa ilorazu wiarygodności
)
(y
l
w zależności od wartości zmiennej losowej y
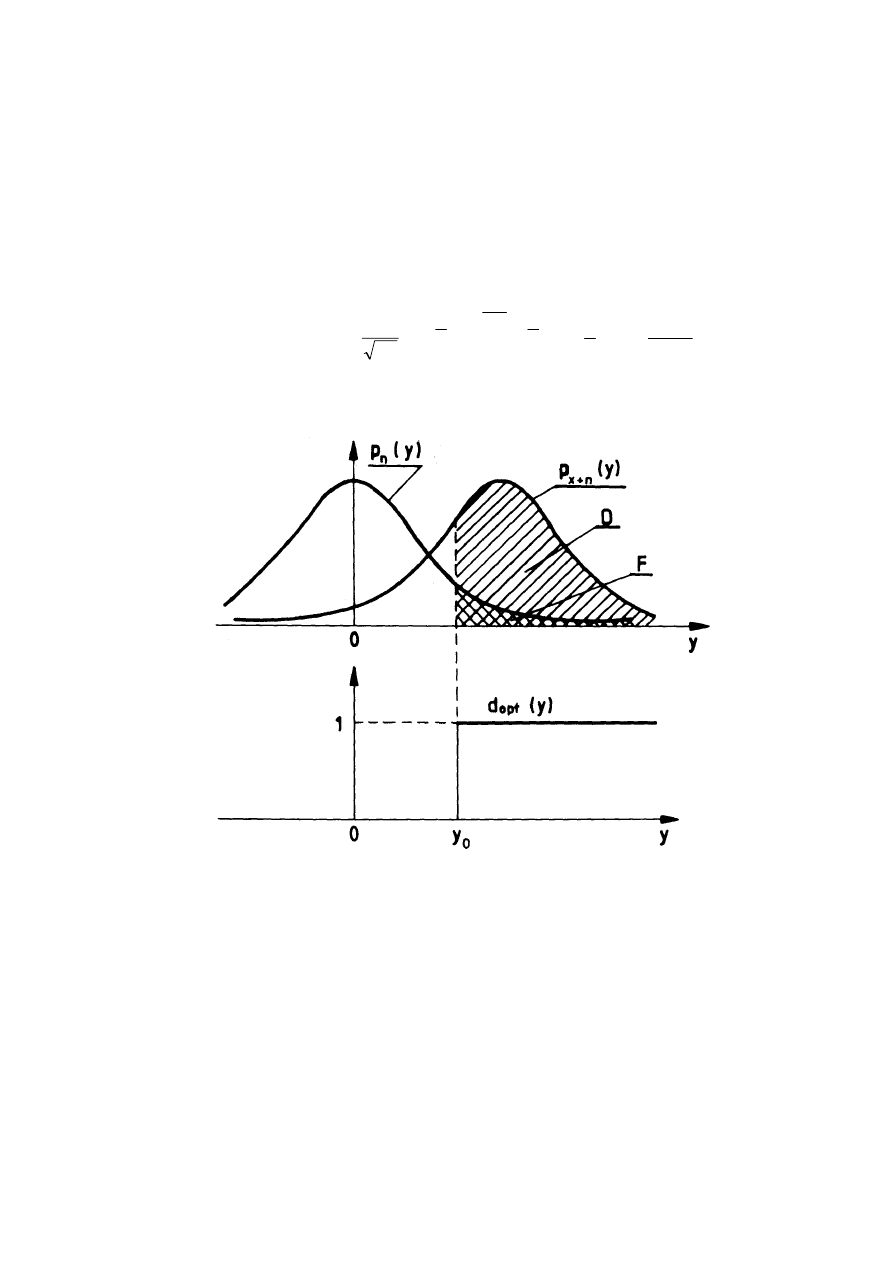
Porównując je z zaproponowaną regułą decyzyjną widać, że tamta nie była
optymalna. Dalej na wykresie 1.3 pokazano przebiegi rozkładów
prawdopodobieństw p
n
(y) i p
x+n
(y) wraz z optymalną regułą decyzyjną.
Prawdopodobieństwo fałszywego alarmu F dla tej reguły odpowiada polu pod
krzywą p
n
(y) dla y
≥
y
0
. Wielkość y
0
nazywana jest progiem detekcji. Przy
założonym poziomie zakłóceń prawdopodobieństwo fałszywego alarmu F
zależy wyłącznie od y
0
,
Φ
−
=
−
=
=
∫
∫
∫
−
∞
−
∞
)
(
1
2
1
2
1
)
(
0
0
2
0
2
0
2
2
0
σ
π
σ
y
ds
ds
dy
y
p
F
y
s
s
y
n
e
e
gdzie
Φ
jest tzw. funkcją błędu. Oznacza to, że wartość progu y
0
można ustalić
bezpośrednio z zakładanego prawdopodobieństwa fałszywego alarmu.
Podejście takie odpowiada wspomnianemu wcześniej kryterium Neymana-
Pearsona [1, 4]. Jest wygodne w zastosowaniach praktycznych, ponieważ
pozwala uniknąć konieczności uwzględnienia prawdopodobieństw a priori
dotyczących obecności lub nieobecności sygnału. W systemach radarowych
odpowiada to prawdopodobieństwom stanów H
1
i H
0
−
odpowiednio P(H
1
) i
21
P(H
0
) czyli obecności i nieobecności obiektu w określonym fragmencie
przestrzeni powietrznej.
Prawdopodobieństwo detekcji D sygnału x odpowiada polu pod krzywą
p
x+n
(y) dla y
≥
y
0
. Przy założonym poziomie zakłóceń
σ
, zależy nie tylko od progu
detekcji y
0
, ale i od oczekiwanej wartości sygnału x, co opisywane jest
zależnością:
−
Φ
−
=
−
=
=
∫
∫
∫
−
−
∞
−
∞
+
)
(
1
2
1
2
1
)
(
0
0
2
0
2
0
2
2
0
σ
π
σ
x
y
ds
ds
dy
y
p
D
x
y
s
s
y
n
x
e
e
Rys. 1.3. Krzywe warunkowych rozkładów prawdopodobieństw zmiennej losowej y dla
prawdziwości hipotezy H
0
−
p
n
(y) i H
1
−
p
x+n
(y) oraz optymalna reguła decyzyjna d
opt
(y)
Na wykresie 1.4 na kolejnej stronie pokazano krzywe zwane charakterystykami
detekcji. Jak widać, im większa jest wartość progu y
0
, czyli mniejsze
prawdopodobieństwo fałszywego alarmu F, tym bardziej w prawo przesuwa się
wykres D(x). Oznacza to, że aby zagwarantować takie samo
prawdopodobieństwo detekcji D potrzebny jest wyższy poziom sygnału
użytecznego x.
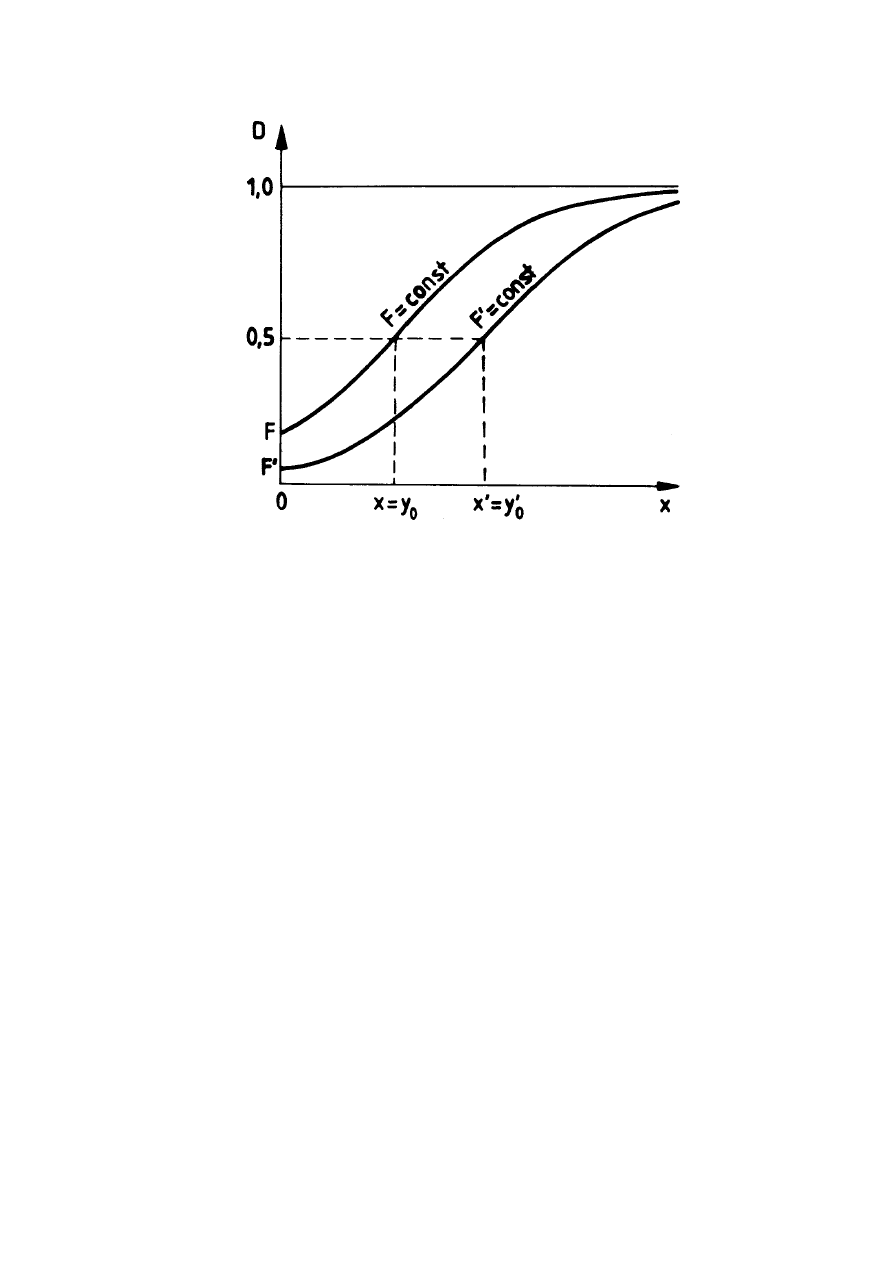
22
Rys. 1.4. Charakterystyki detekcji dla przypadku wskaźnika wychyłowego
1.4. WERYFIKACJA HIPOTEZ ZA POMOCĄ
POMIARÓW WIELOKROTNYCH
Teoria i przykład przedstawiony we wcześniejszych punktach mogą być
łatwo rozszerzone na przypadki, w których wybór jednej z hipotez H
0
lub H
1
dokonywany jest na podstawie większej liczby pomiarów. Mierzone wielkości y
0
,
y
1
, ... y
N-1
mogą reprezentować kolejne pomiary tej samej wielkości fizycznej,
pomiar N różnych parametrów, albo dowolną kombinację tych dwóch
możliwości. Wielkości te mogą być opisane łącznymi, wielowymiarowymi
funkcjami gęstości prawdopodobieństwa p(y/H
0
)=p
0
(y)=p
0
(y
0
, y
1
, ..., y
N-1
) i
p(y/H
1
)=p
1
(y)=p
1
(y
0
, y
1
, ... y
N-1
) odpowiednio dla hipotez H
0
i H
1
. Zadanie polega
na wyborze jednej z tych dwóch funkcji gęstości prawdopodobieństwa, która
lepiej opisuje wynik pomiaru. Słowo „lepiej” należy rozumieć w sensie
odpowiedniego kryterium decyzyjnego wprowadzonego w poprzednich
punktach. Jeśli funkcje p
0
(y) i p
1
(y) nie zawierają nieznanych parametrów, to

23
odpowiadające im hipotezy można nazwać „prostymi”. Obie funkcje gęstości
pomnożone przez dy
0
dy
1
...dy
N-1
określają prawdopodobieństwo zdarzenia
polegającego na tym, że zmienna losowa y
0
przyjmie wartość z przedziału
〈
y
0
,y
0
+dy
0
〉
, y
1
z przedziału
〈
y
1
, y
1
+dy
1
〉
itd. Oczywiście dla obu funkcji gęstości
musi zachodzić związek ,że
1
...
)
,...,
,
(
...
1
1
0
1
1
0
=
⋅
∫∫
∞
∞
−
−
−
N
N
dy
dy
dy
y
y
y
p
W procesie detekcji każdej realizacji (y
0
, y
1
, ..., y
N-1
) należy
przyporządkować konkretną decyzję. Oznacza to, że na zbiorze realizacji może
być określona reguła decyzyjna d(y)=d(y
0
,y
1
,...y
N-1
), przyjmująca w zależności
od swych argumentów dwie wartości: 0 lub 1, którym odpowiadają decyzje d
0
oraz d
1
o nieobecności lub obecności sygnału użytecznego.
Inaczej mówiąc każdemu punktowi wielowymiarowej przestrzeni należy
przypisać odpowiednią wartość: 0 lub 1. Regułę decyzyjną można wtedy
wyrazić jako podział wspomnianej przestrzeni na dwa obszary: R
0
oraz R
1
. Jeśli
wynik pomiaru (punkt) znajduje się w obszarze R
0
, to podejmowana jest
decyzja d
0
o słuszności hipotezy H
0
, zaś gdy punkt leży w obszarze R
1
,
wybierana jest hipoteza H
1
. Obszary R
0
i R
1
są rozdzielone powierzchnią d,
zwaną „powierzchnią decyzyjną”. Regułę decyzyjną można (jak w poprzednim
punkcie dla pojedynczego pomiaru
−
zależność 1.23) opisać zbiorem
nierówności dla N zmiennych y
i
(0
≤
i
≤
N-1).
Aby łatwiej zilustrować sytuację wygodnie jest przedstawić zbiór N
wyników pomiaru geometrycznie, jako jeden punkt w N-wymiarowej przestrzeni
kartezjańskiej o współrzędnych y=(y
0
, y
1
, ..., y
N-1
). Na rysunku 1.5 pokazano
przykładowe obszary decyzji i powierzchnię decyzyjną dla N=2. Położenie i
kształt powierzchni decyzyjnej d zależy od wybranego kryterium
−
inne będzie
dla ogólnego kryterium minimum ryzyka, a inne dla kryterium Neymana-
Pearsona.
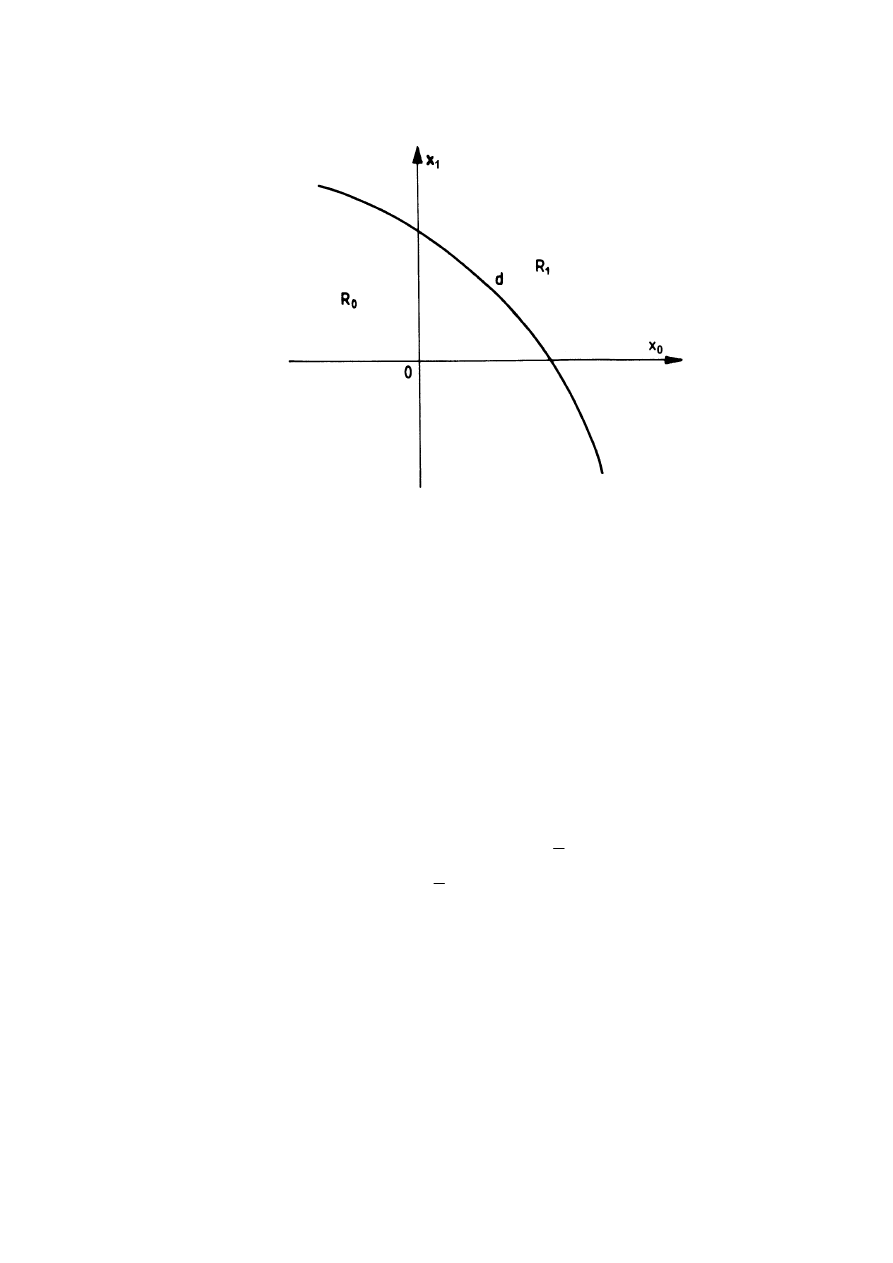
24
Rys. 1.5. Obszary decyzyjne dla dwóch pomiarów (N=2) oddzielone powierzchnią decyzyjną d
Jeśli znane są koszty błędnych decyzji (dla poprawnych można przyjąć
zerowy koszt) tzn. straty dla fałszywego alarmu oraz przeoczenia obiektu w
przestrzeni, oraz bezwarunkowe prawdopodobieństwa a priori P(H
0
) i P(H
1
)
odpowiednio dla hipotez H
0
i H
1
, można zastosować ogólne kryterium Bayesa
polegające na minimalizacji ryzyka.
W sytuacji, gdy nie jest możliwa ocena prawdopodobieństw a priori P(H
0
) i
P(H
1
), a także nie są dokładnie znane koszty towarzyszące różnym decyzjom,
dogodne jest zastosowanie kryterium Neymana-Pearsona. Wymaga ono
takiego położenia powierzchni decyzyjnej d, aby zminimalizować
prawdopodobieństwo przepuszczenia obiektu D (czyli zmaksymalizować
prawdopodobieństwo detekcji D=1-D ), wtedy gdy narzucone jest dopuszczalne
prawdopodobieństwo fałszywego alarmu F. Obserwator w jakiś sposób
decyduje o odpowiednim doborze prawdopodobieństwa F. Zwiększanie go
oznacza zwiększenie prawdopodobieństwa D, czemu odpowiada dokładniejsze
stwierdzenie występowania hipotezy H
1
. Posługując się analogią do
jednowymiarowego przykładu detekcji łatwo można znaleźć optymalną
powierzchnię d i odpowiadającą jej regułę decyzyjną d(y)=d(y
0
, y
1
, ..., y
N-1
).
Prawdopodobieństwa fałszywego alarmu oraz detekcji dla dowolnej funkcji
decyzyjnej można zapisać jak dalej (analogicznie do wzorów 1.19, 1.20):

25
∫∫
∞
∞
−
⋅
⋅
=
...
)
,...
,
(
,...)
,
(
...
1
0
1
1
0
1
0
dy
dy
H
y
y
p
y
y
d
D
(1.24)
∫∫
∞
∞
−
⋅
⋅
=
...
)
,...
,
(
,...)
,
(
...
1
0
0
1
0
1
0
dy
dy
H
y
y
p
y
y
d
F
(1.25)
Dla wyboru optymalnej reguły można się posłużyć jak poprzednio wyrażeniem
na kryterium wagowe: D-
0
l
F. Można je przedstawić w poniższej postaci:
[
]
∫∫
∞
∞
−
⋅
−
⋅
⋅
=
−
...
,...)
,
(
)
,...
,
(
,...)
,
(
...
1
0
0
1
0
0
1
0
1
0
0
dy
dy
l
y
y
l
H
y
y
p
y
y
d
F
l
D
(1.26)
gdzie
)
,...
,
(
)
,...
,
(
,...)
,
(
0
1
0
1
1
0
1
0
H
y
y
p
H
y
y
p
y
y
l
=
jest stosunkiem wiarygodności. Ponieważ optymalnym z punktu widzenia
kryterium wagowego jest rozwiązanie dające maksimum powyższej całki,
otrzymuje się je tak samo jak dla wykrywania jednowymiarowego w poprzednim
punkcie (wzór. 1.22):
<
>
=
0
1
0
0
1
0
1
0
,...)
,
(
0
,...)
,
(
1
,...)
,
(
l
y
y
l
dla
l
y
y
l
dla
y
y
d
opt
(1.27)
Znając postać stosunku wiarygodności można przekształcić zapis powyższej
reguły decyzyjnej uzależniając ją od zmiennych (y
0,
y
1
,...) i wartości progowej Y
0
uzyskując dzięki temu wyrażenie na powierzchnię decyzyjną d.
Tak więc optymalna powierzchnia decyzyjna d, dzieląca przestrzeń
realizacji na obszary R
0
i R
1
jest jedną z rodziny powierzchni, określonych przez
parametr
0
l
. Wybrana jest taka wartość parametru, dla której
prawdopodobieństwo fałszywego alarmu F równe jest wartości narzuconej.
Kryterium Neymana-Pearsona prowadzi do procedury, w której stosunek
wiarygodności porównywany jest z ustaloną wartością
0
l
; wybiera się hipotezę
H
0
jeżeli
l
(x)<
0
l
, a hipotezę H
1
, jeśli
l
(x)>
0
l
.
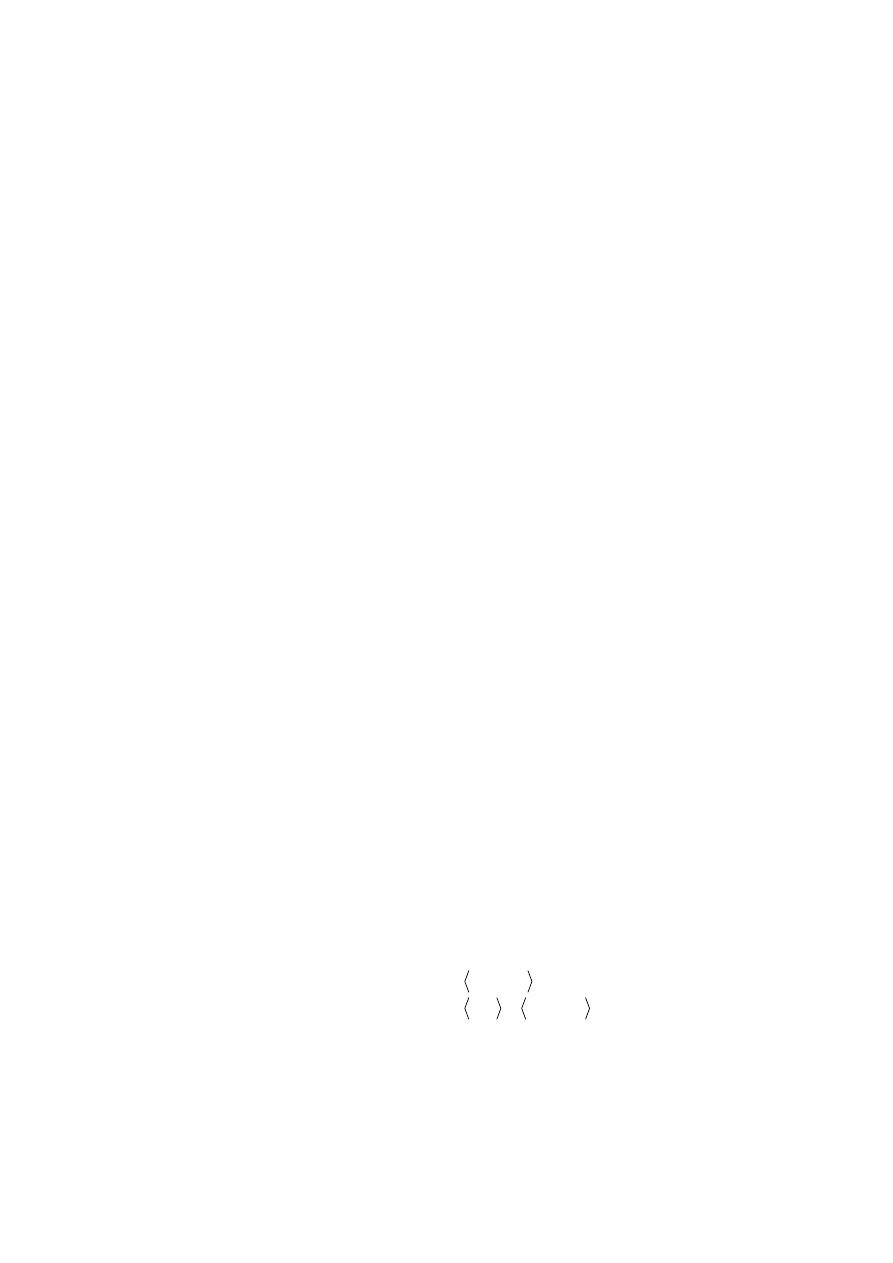
26
1.5. PRZYKŁAD OPTYMALNEJ DETEKCJI NA
PODSTAWIE WIELU POMIARÓW
Teorię przedstawioną w punktach 1.1
−
1.3 w połączeniu z rozważaniami z
punktu ostatniego 1.4 można zastosować rozważając przykładowy problem
detekcji sygnału x(t), którego wszystkie parametry (jak amplituda, faza, kształt
oraz czas pojawienia się) są znane.
Sygnał x(t) może występować w obecności białego szumu gaussowskiego
n(t) o wartości oczekiwanej równej zero. Obserwator odbiera sygnał wejściowy
y(t) będący np. echem radarowym odbitym od jakiegoś obiektu, obserwowanym
w czasie 0
<
t
<
T, zwanym przedziałem obserwacji.
Na podstawie przebiegu y(t) musi zostać podjęta decyzja odnośnie
wyboru jednej z dwóch możliwych hipotez prostych: H
0
−
że sygnał użyteczny
nie występuje i odebrany przebieg zawiera tylko szum tzn.
)
(
)
(
t
n
t
y
=
albo hipotezę H
1
−
że sygnał odebrany składa się z sumy oczekiwanego
sygnału i szumu:
)
(
)
(
)
(
t
n
t
x
t
y
+
=
Powyższe wyrażenia różnią się od tych występujących w przypadku
jednowymiarowym (wskaźnik wychyłowy) tym, że tutaj występują funkcje
czasu. Przyjęte zostało pewne kryterium, zapewniające sukces przy dużej
liczbie podejmowanych decyzji tego typu, będące miarą poprawności
działania (wybór kryterium ma wpływ na sposób oceny zbieranych
danych).
Przykładowym sygnałem użytecznym może być impuls prostokątny o
czasie trwania T
1
<
T, występującym w określonym (znanym) czasie wewnątrz
przedziału obserwacji:
+
∪
∈
+
∈
=
T
T
t
t
t
dla
T
t
t
t
dla
A
t
x
;
;
0
0
;
)
(
1
1
1
1
1
1
(1.28)
Po zakończeniu obserwacji (po czasie T) podejmowana jest decyzja o
obecności lub nieobecności sygnału. Istnienie szumu powoduje popełnianie
przypadkowych błędów i zadaniem obserwatora jest minimalizacja
prawdopodobieństwa ich popełnienia.

27
Rozważania i wyprowadzenie reguł decyzyjnych w poprzednich punktach
prowadzono przy założeniu skończonej liczby obserwacji. Jednak zgodnie z
twierdzeniem o próbkowaniu każdy sygnał o ograniczonym paśmie do jakiejś
częstotliwości f
max
można poddać dyskretyzacji, nie tracąc informacji w nim
zawartych, jeśli tylko częstotliwość próbkowania nie będzie mniejsza od 2f
max
[13]. Każdej chwili próbkowania t
k
(0
≤
k
≤
N-1) można przypisać trójkę liczb
określającą wartości sygnałów: x
k
=x(t
k
), n
k
=n(t
k
) oraz y
k
=y(t
k
) odpowiednio dla
sygnału użytecznego, zakłócenia i ich sumy. Istnieje zatem możliwość opisania
przypadkowych funkcji czasu za pomocą równoważnych im wielowymiarowych
zmiennych losowych. Obserwator wybiera jedną z dwóch hipotez na podstawie
wielu wartości y
k
. Wartości te charakteryzowane są przez łączne N-wymiarowe
funkcje gęstości prawdopodobieństwa:
)
,...,
,
(
1
1
0
0
−
N
y
y
y
p
oraz
)
,...,
,
(
1
1
0
1
−
N
y
y
y
p
pod warunkiem, że prawdziwa jest odpowiednio hipoteza H
0
albo H
1
.
Podejmując decyzję można się opierać na wartości stosunku wiarygodności
)
,...,
,
(
)
,...,
,
(
)
,...,
,
(
1
1
0
0
1
1
0
1
1
1
0
−
−
−
=
N
N
N
y
y
y
p
y
y
y
p
y
y
y
l
który porównywany jest z wartością progową
0
l
. Jeśli
l
(y)<
0
l
, podejmowana
jest decyzja d
0
, że słuszna jest hipoteza H
0
(odebrano tylko zakłócenia), jeśli
l
(y)
>
0
l
podejmowana jest decyzja d
1
tzn. że odebrano sygnał użyteczny.
Wielkość
0
l
zależy od wybranego kryterium decyzyjnego.
W przypadku, gdy n(t) jest gaussowskim szumem białym, to zmienne
losowe y
k
są statystycznie niezależne i jeśli prawdziwa jest hipoteza H
0
, to
łączna funkcja gęstości prawdopodobieństwa wynosi [3, 12]:
)
2
exp(
)
2
(
)
,...,
,
(
1
0
2
2
2
2
1
1
0
0
∑
−
=
−
−
−
⋅
=
N
k
k
N
N
y
y
y
y
p
σ
πσ
(1.29)
Gdy istnieje sygnał użyteczny (prawdziwa hipoteza H
1
), to łączna funkcja
gęstości prawdopodobieństwa jest dana przez powyższe wyrażenie, z tym że y
k
zastąpiono przez (y
k
-x
k
).

28
Inaczej mówiąc wielkości y
k
są niezależnymi zmiennymi losowymi o wartości
oczekiwanej x
k
:
)
2
)
(
exp(
)
2
(
)
,...,
,
(
1
0
2
2
2
2
1
1
0
1
∑
−
=
−
−
−
−
⋅
=
N
k
k
k
N
N
x
y
y
y
y
p
σ
πσ
(1.30)
Stosunek wiarygodności ma postać:
)
2
2
exp(
)
,...,
,
(
1
0
2
2
1
1
0
∑
−
=
−
−
=
N
k
k
k
k
N
x
y
x
y
y
y
l
σ
(1.31)
Jeśli
l
(y)<
0
l
podejmowana jest decyzja d
0
. Logarytmując i przekształcając tą
nierówność dostaje się:
0
2
1
0
2
1
0
ln
2
1
l
x
y
x
N
k
k
N
k
k
k
σ
+
<
∑
∑
−
=
−
=
(1.32)
Tak więc decyzję można podejmować opierając się na wartości poniższej
statystyki
∑
−
=
=
1
0
N
k
k
k
N
y
x
G
(1.33)
i porównywaniu jej z ustaloną wartością G
0
.
W N-wymiarowej przestrzeni realizacji zmiennych losowych y
k
powierzchnia decyzyjna d jest hiperpłaszczyzną
const
y
x
N
k
k
k
=
∑
−
=
1
0
do której jest prostopadły wektor o współrzędnych x
k
.
Zapisując wyrażenie na statystykę G
N
dla sygnałów z ciągłym czasem
dochodzi się do poniższej całki:
∫
=
T
dt
t
y
t
x
G
0
)
(
)
(
zwanej całką korelacyjną. O systemie decyzyjnym, w którym statystyka G
N
lub
G jest porównywana z pewnym progiem G
0
, można powiedzieć, że wzajemnie
koreluje sygnał wejściowy y(t) z sygnałem oczekiwanym x(t). System taki
nazywa się detektorem korelacyjnym. Jeżeli G
N
<G
0
, przyjmuje się, że
prawdziwa jest hipoteza H
0
−
"sygnału nie ma", jeśli G
N
>G
0
wybierana jest
hipoteza H
1
−
"sygnał jest". Wielkość G
0
jest zależna od stosowanego kryterium
decyzyjnego. Przy zastosowaniu kryterium Neymana-Pearsona wartość
prawdopodobieństwa fałszywego alarmu F jest z góry ustalona, zwykle na
podstawie względnej liczby błędów I rodzaju, jaką obserwator może dopuścić.
29
Statystyka G
N
jest zmienną losową opisaną przez jedną z dwóch funkcji
gęstości prawdopodobieństwa: p
1
(G
N
) i p
0
(G
N
) odpowiednio gdy sygnał
użyteczny jest zawarty w sygnale y(t) oraz gdy go nie ma. Ponieważ G
N
jest
kombinacją liniową zmiennych losowej y(t) mających rozkład Gaussa, także jest
zmienną losową gaussowską. Jeśli prawdziwa jest hipoteza H
0
, to wartość
oczekiwana (średnia) statystyki G
N
równa jest
0
=
N
EG
bo E[n(t)]=0. W przypadku prawdziwości hipotezy H
1
, wartość średnia sygnału
wejściowego y(t) w każdej chwili wynosi x(t), gdyż sygnał i szum się dodają.
Wartość oczekiwana EG
N
(łatwo ją wyliczyć korzystając z własności wartości
oczekiwanej) [12] wynosi wtedy
x
N
k
k
N
E
x
EG
=
=
∑
−
=
1
0
2
(1.34)
i jest równa energii sygnału x(t). Co do wariancji, to są one takie same w
przypadku obu hipotez i wynoszą:
x
N
k
k
N
E
x
G
D
2
1
0
2
2
2
σ
σ
=
⋅
=
∑
−
=
(1.35)
Funkcje gęstości prawdopodobieństwa statystyki G
N
mogą być zapisane
według poniższych równań:
)
2
exp(
2
1
)
(
2
4
2
0
x
N
x
N
E
G
E
G
p
σ
σ
π
−
=
)
2
)
(
exp(
2
1
)
(
2
4
2
1
x
x
N
x
N
E
E
G
E
G
p
σ
σ
π
−
−
=
Jeżeli G
N
>G
0
i sygnału nie ma popełnia się błąd I rodzaju (podnosi się
fałszywy alarm). Prawdopodobieństwo fałszywego alarmu wynosi
∫
∞
=
0
)
(
0
G
N
N
dG
G
p
F
(1.36)
Jeśli podejmuje się decyzję d
1
tzn. stwierdza się istnienie sygnału, gdy
rzeczywiście występuje (G
N
>G
0
, gdy hipoteza H
1
jest prawdziwa) oznacza to,
że wykryto sygnał x(t).

30
Prawdopodobieństwo detekcji (jego wykrycia) wynosi
∫
∞
=
0
)
(
1
G
N
N
dG
G
p
D
(1.37)
Z drugiej strony, gdy G
N
<G
0
, a sygnał występuje, popełniany jest błąd II rodzaju,
czyli przeocza się sygnał użyteczny. Prawdopodobieństwo błędu przeoczenia
wynosi 1-D.
2. ANALIZA UKŁADÓW OPTYMALNEJ DETEKCJI
RZECZYWISTYCH SYGNAŁÓW RADAROWYCH
2.1. DETEKCJA SYGNAŁU O NIEZNANYCH PARAMETRACH
W poprzednim rozdziale rozpatrywano optymalne metody detekcji i
problemy z nimi związane w przypadku, kiedy oczekiwany sygnał, który należy
wykryć jest całkowicie znany. Podejmowanie decyzji odnośnie dwóch hipotez
prostych H
0
i H
1
na podstawie ustalonej liczby pomiarów polegało na wyborze
jednej z dwóch funkcji gęstości prawdopodobieństwa p
0
(y) oraz p
1
(y), bardziej
odpowiadającej zaobserwowanym wartościom y=(y
0
, y
1
, ..., y
N-1
) N zmiennych
losowych. Wybór ten miał być optymalny ze względu na przyjęte kryterium
decyzyjne (Bayesa lub Neymana-Pearsona), zapewniające sukces
statystycznie w większości sytuacji. Zakładano przy tym, że w oba rozkłady
prawdopodobieństwa były całkowicie znane.
W rzeczywistych systemach takie idealne sytuacje należą do rzadkości.
Często zdarza się, że jedna lub obie funkcje gęstości prawdopodobieństwa
p
0
(y) i p
1
(y) zależą od pewnego zbioru M parametrów
β
0
,
β
1
, ...,
β
M-1
, których

31
wartości nie są znane obserwatorowi. Wtedy znalezienie optymalnych kryteriów
decyzyjnych staje się trudniejsze.
W niniejszym rozdziale rozpatrzona zostanie sytuacja, gdy rozkład p
0
(y)
odpowiadający hipotezie H
0
tzn. gdy y(t)=n(t) nie zależy od żadnych nieznanych
parametrów, natomiast p
1
(y) odpowiadający hipotezie H
1
tzn. y(t)=x(t)+n(t)
zależy od M parametrów, których zbiór można traktować jako wektor
ββββ
=(
β
0
,
β
1
,...,
β
M-1
) w pewnej M-wymiarowej przestrzeni parametrów. Jeśli
składowe wektora
ββββ
są zmiennymi losowymi, to funkcja rozkładu p
1
(y/
ββββ
) jest
warunkową funkcją gęstości prawdopodobieństwa. Hipoteza H
0
zwana jest
wtedy prostą, a H
1
złożoną. Badaną regułę decyzyjną opisuje się jak
poprzednio tzn. przez podział N-wymiarowej przestrzeni kartezjańskiej wartości
próbek y
k
na obszary R
0
i R
1
. Wybiera się hipotezę H
0
, gdy punkt o
współrzędnych danych przez zmierzone wartości y=(y
0
,y
1
,...,y
N-1
) leży na
obszarze R
0
, zaś H
1
−
gdy należy do R
1
. Powierzchnię d wybiera się tak, aby
reguła decyzyjna była w pewnym sensie optymalna.
Przykładowo w rzeczywistych systemach radarowych funkcja gęstości
prawdopodobieństwa p
0
(y) jest funkcją n próbek przebiegu wejściowego y(t)
zawierającego jedynie szum (zwykle biały o rozkładzie Gaussa), zaś funkcja
p
1
(y/
ββββ
) jest funkcją gęstości prawdopodobieństwa tych samych obserwacji
przebiegu wejściowego, gdy odbiera się także sygnał użyteczny x(t,
ββββ
), gdzie
składowe wektora
ββββ
reprezentują pewne parametry sygnału. Impulsowy sygnał
wąskopasmowy wysyłany przez radar da się zapisać jako:
)]
(
cos[
)
(
0
t
t
A
t
s
−
=
ω
gdzie A jest znaną amplitudą,
ω
−
pulsacją, a t
0
chwilą wysłania impulsu.
Jednak sygnał echa radarowego w zależności od tego, gdzie jest i jak się
zachowuje cel, ma już wiele nieznanych parametrów. Można go przedstawić
poniższym wyrażeniem:
)
,
,
(
)
(
)
,
(
)
(
)
,
(
x
d
op
op
t
t
s
t
X
t
t
s
t
X
t
x
ϕ
ω
β
β
−
⋅
=
−
⋅
=
gdzie:
β
0
=X(t)
−
amplituda sygnału;
β
1
=t
op
−
opóźnienie wynikające z odległości celu od radaru;
β
2
=
ω
d
−
pulsacja dopplerowska zależna od prędkości celu;
β
3
=
ϕ
x
−
faza sygnału.
32
Obserwator może znać tylko niektóre z parametrów lub szerokie granice, w
jakich się one zmieniają. Można zatem powiedzieć, że próbuje wykryć jeden z
sygnałów należących do zbioru wykluczających się sygnałów o postaci jak
wyżej.
Najbardziej ogólnym, chociaż rzadko w praktyce spotykanym jest
przypadek, gdy wszystkie prawdopodobieństwa a priori: P(H
0
), P(H
1
), łączna
funkcja gęstości prawdopodobieństwa parametrów p(
ββββ
) oraz koszty są dobrze
określone. Można wtedy stosować kryterium Bayesa polegające na
minimalizacji ryzyka.
Jeśli P(H
0
), P(H
1
) i koszty decyzji nie są znane (sytuacja typowa w
systemach radarowych), stosuje się kryterium Neymana-Pearsona.
Prawdopodobieństwo błędu I rodzaju (fałszywego alarmu) wynosi
∫
−
−
=
1
1
0
1
0
0
...
)
,...,
(
R
N
N
dy
dy
y
y
p
F
gdzie R
1
jest obszarem przestrzeni próbek y
k
, w którym prawdziwa jest hipoteza
H
1
. Prawdopodobieństwo błędu II rodzaju (przepuszczenia obiektu) w
przypadku detekcji sygnałów z nieznanymi parametrami
ββββ
jest teraz funkcją
tych parametrów:
∫
−
−
−
=
0
1
0
1
0
1
0
1
...
)
,...,
,...,
(
)
(
R
N
M
N
dy
dy
y
y
p
D
β
β
β
podobnie R
0
jest obszarem, na którym wybierana jest hipoteza H
0
. Dla
zadanego zbioru wartości parametrów
ββββ
powierzchnia decyzyjna d
rozdzielająca obszary R
0
i R
1
powinna być taka, aby dla ustalonego poziomu F
prawdopodobieństwo
)
(
β
D
było minimalne.
Przy stosowaniu kryterium Neymana-Pearsona najwygodniejszy jest
przypadek, gdy usytuowanie powierzchni d minimalizujące
)
(
β
D
dla zadanego
F, nie zależy od wartości parametrów. Wtedy ta sama powierzchnia decyzyjna d
jest optymalna dla wszystkich wartości
ββββ
i dla funkcji gęstości
prawdopodobieństwa zmiennej
ββββ
mówi się, że strategia stanowi jednostajnie
najmocniejszy test hipotezy H
1
względem hipotezy H
0
. Zilustrować to można na
poniższym przykładzie: niech próbki y będą niezależnymi zmiennymi losowymi
o rozkładach Gaussa z wariancją
σ
2
i niech wartość średnia x wynosi zero przy

33
hipotezie H
0
i x>0 przy hipotezie H
1
. Wtedy łączne funkcje gęstości
prawdopodobieństwa mają postać:
)
2
)
(
exp(
)
2
(
)
,
(
)
2
exp(
)
2
(
)
(
1
0
2
2
2
2
1
1
0
2
2
2
2
0
∑
∑
−
=
−
−
=
−
−
−
⋅
=
−
⋅
=
N
k
k
N
N
k
k
N
x
y
x
y
p
y
y
p
σ
πσ
σ
πσ
O wartości średniej x wiadomo tylko tyle, że jest dodatnia. Dla ustalonej
wartości x wyliczywszy stosunek wiarygodności
l
(y), który porównywany byłby
z progiem
0
l , logarytmując następnie nierówność
l
(y)<
0
l stronami i
odpowiednio przekształcając uzyskuje się optymalną regułę decyzyjną, która
jest równoważna porównywaniu średniej
∑
−
=
=
1
0
1
N
k
k
y
N
Y
z pewną ustaloną wartością graniczną Y
0
określoną przez poniższe wyrażenie:
2
ln
0
2
0
x
Nx
l
Y
+
=
σ
Hipotezę H
0
wybiera się gdy Y<Y
0
, zaś H
1
gdy Y>Y
0
. Wartość graniczną ustala
się tak, aby uzyskać żądany poziom prawdopodobieństwa fałszywego alarmu
zgodnie ze wzorem, że
∫
∞
=
0
)
(
0
Y
dY
Y
p
F
gdzie p
0
(Y) jest rozkładem Gaussa o zerowej średniej i wariancji
σ
2
/N.
Powierzchnia decyzyjna d jest w tym przypadku płaszczyzną
0
1
0
NY
y
N
k
k
=
∑
−
=
i jest niezależna od istniejącej przy hipotezie H
1
średniej x. Dlatego test jest
jednostajnie najmocniejszy, gdy występująca średnia x jest dodatnia i może być
stosowany nawet wtedy, gdy aktualna wartość x nie jest znana. Niestety raczej
wyjątkowo powierzchnia decyzyjna jest niezależna od parametrów
ββββ
. W wielu
przypadkach jedna i ta sama powierzchnia d(
ββββ
) nie jest optymalna dla
wszystkich możliwych wartości
ββββ
, a więc test jednostajnie najmocniejszy nie
istnieje. Tak jest na przykład, kiedy średnia x z powyższego przykładu może
być dodatnia lub ujemna. Należy wtedy skorzystać z danej funkcji gęstości

34
prawdopodobieństwa a priori p(
ββββ
) jeśli jest znana, lub wybrać pewną funkcję
gęstości prawdopodobieństwa p(
ββββ
) dobrze opisującą zjawisko i minimalizować
prawdopodobieństwo błędu II rodzaju uśrednione względem wszystkich
możliwych kombinacji parametrów:
β
β
β
β
β
β
β
M
R
N
M
śr
d
y
p
p
y
d
d
D
p
D
)
(
)
(
)
(
)
(
)
(
1
0
∫
∫
∫
⋅
=
⋅
=
.
Obserwator musi się zadowolić regułą, która jest poprawna tylko w odniesieniu
do zbioru możliwych wartości parametrów
ββββ
o rozkładzie zgodnym z przyjętym.
Może jednak istnieć jeden rozkład p
max
(
ββββ
), dla którego znaleziona wartość
)
(
β
śr
D
jest największa. Jest to najmniej korzystny rozkład przy kryterium
Neymana-Pearsona. W sytuacji, gdy wartości parametrów są nieznane
rozsądne jest stosowanie w kryterium Neymana-Pearsona najmniej
korzystnego rozkładu parametrów, ponieważ obserwator może być pewny, że
jego strategia daje założone przez niego prawdopodobieństwo fałszywego
alarmu F oraz prawdopodobieństwo przeoczenia obiektu nigdy nie przekroczy
wartości
)
(
)
(
)
(
max
β
β
β
p
p
D
śr
=
niezależnie od tego, który zbiór wartości parametrów rzeczywiście wystąpi w
następnych próbach [4].
2.2. STOSUNEK WIARYGODNOŚCI DLA SYGNAŁU
O NIEZNANYCH PARAMETRACH
W punkcie 1.5 wyprowadzono wyrażenie na stosunek wiarygodności dla
sygnału całkowicie znanego, pojawiającego się w obecności szumu białego o
rozkładzie Gaussa. W niniejszym punkcie wyprowadzone zostanie wyrażenie
na stosunek wiarygodności dla sygnału o nieznanych parametrach.
W sytuacji, gdy odbierany przebieg składa się z sygnału użytecznego o
nieznanych parametrach oraz zakłóceń, można go zapisać poniższą sumą:

35
)
(
)
,...,
,
,
(
)
(
1
1
0
t
n
t
x
t
y
M
+
=
−
β
β
β
Dyskretne wartości y
k
=y(t
k
) i zbiór parametrów
ββββ
można opisać łączną funkcją
gęstości prawdopodobieństwa. Jeśli założyć, że rozkład parametrów p(
ββββ
) jest
znany, to zgodnie z twierdzeniem Bayesa można zapisać jak niżej:
)
,...,
,...,
(
)
,...,
(
)
,...,
,...,
(
)
,...,
(
)
,...,
,
,...,
(
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
−
−
−
−
−
−
−
−
⋅
=
=
⋅
=
M
N
M
N
M
N
M
N
y
y
p
p
y
y
p
y
y
p
y
y
p
β
β
β
β
β
β
β
β
(2.1)
Całkowanie w nieskończonym przedziale bezwarunkowych lub warunkowych
gęstości prawdopodobieństwa daje zawsze jeden, tak więc:
∫ ∫
∞
∞
−
∞
∞
−
−
−
−
=
1
...
)
,...,
,...,
(
...
1
0
1
0
1
0
M
N
M
d
d
y
y
p
β
β
β
β
Całkując wyrażenie (2.1) dostaje się:
∫ ∫
∞
∞
−
∞
∞
−
−
−
−
−
−
⋅
=
1
0
1
0
1
0
1
0
1
0
...
)
,...,
,...,
(
)
,...,
(
...
)
,...,
(
M
M
N
M
N
d
d
y
y
p
p
y
y
p
β
β
β
β
β
β
(2.2)
Ponieważ p(y
0
,...,y
N-1
)=p
1
(y
0
,...,y
N-1
), lewa strona wyrażenia (2.2) jest gęstością
prawdopodobieństwa realizacji wielkości y
k
, przy założeniu odebrania sygnału
wraz z zakłóceniami, mającymi rozkład a priori p(
ββββ
). Jeśli podzielić wyrażenie
(2.2) stronami przez gęstość prawdopodobieństwa tych samych wielkości y
k
,
przy założeniu odebrania jedynie zakłóceń p
0
(y
0
,...,y
N-1
), to uzyska się poniższe
wyrażenie na stosunek wiarygodności dla sygnału o nieznanych parametrach:
∫ ∫
∞
∞
−
∞
∞
−
−
−
−
−
−
−
=
1
0
1
0
0
1
0
1
0
1
0
1
0
...
)
,...,
(
)
,...,
,...,
(
)
,...,
(
...
)
,...,
(
M
N
M
N
M
N
d
d
y
y
p
y
y
p
p
y
y
l
β
β
β
β
β
β
(2.3)
Mianownik został wprowadzony pod znak całki, ponieważ nie zależy od
zmiennych całkowania. Wielkość
)
,...,
,...,
(
)
,...,
(
)
,...,
,...,
(
1
0
1
0
1
0
0
1
0
1
0
−
−
−
−
−
=
M
N
N
M
N
y
y
l
y
y
p
y
y
p
β
β
β
β
przedstawia szczególną wartość stosunku wiarygodności dla
ustalonych wartości parametrów. Innymi słowy jest to stosunek
wiarygodności dla sygnału całkowicie znanego. Z powodu
występowania w nim warunkowej gęstości prawdopodobieństwa
często określa się go jako warunkowy stosunek wiarygodności.
Natomiast stosunek wiarygodności sygnału z nieznanymi
parametrami uzyska się w wyniku uśrednienia warunkowego

36
stosunku wiarygodności względem wszystkich parametrów
występujących w warunku:
∫ ∫
∞
∞
−
∞
∞
−
−
−
−
−
−
=
1
0
1
0
1
0
1
0
1
0
...
)
,...,
,...,
(
)
,...,
(
...
)
,...,
(
M
M
N
M
N
d
d
y
y
l
p
y
y
l
β
β
β
β
β
β
Jeśli sygnał użyteczny odbierany jest razem z addytywnym szumem
białym o rozkładzie Gaussa, to biorąc pod uwagę rozważania z
punktu 1.5, a w szczególności wyrażenie (1.31) na stosunek
wiarygodności oraz (1.33) na statystykę G
N
i (1.34) na energię E
x
sygnału x(t) warunkowy stosunek wiarygodności można zapisać
jako:
)
2
)
(
exp(
)
)
(
exp(
)
2
)
(
)
(
)
(
2
exp(
)
,...,
,...,
(
2
2
1
0
2
2
1
0
1
0
σ
β
σ
β
σ
β
β
x
N
N
k
M
N
E
G
k
x
k
y
k
x
y
y
l
−
⋅
=
−
=
∑
−
=
−
−
gdzie
∑
∑
−
=
−
=
=
=
1
0
2
1
0
)
(
)
(
)
(
)
(
)
(
N
k
x
N
k
N
k
x
E
k
y
k
x
G
β
β
w których to wyrażeniach wartości x(k) zależą od wektora
parametrów
ββββ
, zaś
σ
jest odchyleniem standardowym szumu.
Ostatecznie stosunek wiarygodności dla sygnału o nieznanych
parametrach będzie miał poniższą postać:
∫ ∫
∞
∞
−
∞
∞
−
−
−
−
−
⋅
⋅
=
1
0
2
2
1
0
1
0
...
)
2
)
(
exp(
)
)
(
exp(
)
,...,
(
...
)
,...,
(
M
x
N
M
N
d
d
E
G
p
y
y
l
β
β
σ
β
σ
β
β
β
(2.4)
2.3. STOSUNEK WIARYGODNOŚCI DLA SYGNAŁU
O NIEZNANEJ FAZIE

37
Pokazane w punkcie 2.2 zależności, zwłaszcza wyrażenie (2.4) posłużą do
określenia stosunku wiarygodności w przypadku, gdy odbierany użyteczny sygnał
echa ma przypadkową fazę. Po dokonaniu próbkowania jego dyskretny
odpowiednik można zapisać jak poniżej:
]
)
(
cos[
)
(
)
,
(
β
ϕ
θ
β
+
+
=
n
n
n
X
n
x
x
(2.5)
Zgodnie z rozważaniami z poprzedniego punktu zostanie przyjęty najmniej
korzystny rozkład prawdopodobieństwa fazy tzn. równomierny:
)
π
β
π
β
β
2
;
0
2
1
)
(
)
(
max
∈
=
=
dla
p
p
(2.6)
Przekształcając postać (2.5) z zastosowaniem wzoru na sumę
cosinusa sumy, otrzymuje się, że:
β
ϕ
θ
β
ϕ
θ
β
sin
)]
(
sin[
)
(
cos
)]
(
cos[
)
(
)
,
(
n
n
n
X
n
n
n
X
n
x
x
x
+
−
+
=
Oznaczając
)]
(
sin[
)
(
)
(
)]
(
cos[
)
(
)
(
2
1
n
n
n
X
n
x
n
n
n
X
n
x
x
x
ϕ
θ
ϕ
θ
+
−
=
+
=
można zapisać x(n,
β
) jak niżej:
β
β
β
sin
)
(
cos
)
(
)
,
(
2
1
n
x
n
x
n
x
+
=
.
Wobec tego statystyka G
N
może być zapisana jako
∑
−
=
+
=
=
1
0
2
1
sin
cos
)
(
)
,
(
)
(
N
k
N
z
z
k
y
k
x
G
β
β
β
β
,
gdzie
∑
∑
−
=
−
=
=
=
1
0
2
2
1
0
1
1
)
(
)
(
)
(
)
(
N
k
N
k
k
y
k
x
z
k
y
k
x
z
Jeśli potraktować z
1
i z
2
jako współrzędne punktu w prostokątnym
układzie współrzędnych, to można wprowadzić współrzędne
biegunowem Z i
α
określone jako
2
2
2
1
z
z
Z
+
=
(2.7)

38
Z
z
Z
z
2
1
sin
cos
=
=
α
α
i wtedy otrzyma się ostateczną postać statystyki G
N
:
)
cos(
)
sin
sin
cos
(cos
α
β
α
β
α
β
−
=
+
=
Z
Z
G
N
(2.8)
Pozostaje znależć jeszcze energię sygnału E
x
(
β
). Przyglądając się
wartości poniższej całki z funkcji cos
2
(ax+b):
∫
+
+
=
+
)
(
2
sin
4
1
2
)
(
cos
2
b
ax
a
x
dx
b
ax
która odpowiada sumie dla sygnałów z ciągłym czasem, widać że
jeśli amplituda X(n) oraz faza
ϕ
x
(n) sygnału x(n) zmienia się
nieznacznie podczas okresu wielkiej częstotliwości, to energia
sygnału nie zależy praktycznie od fazy i
x
x
E
E
=
)
(
β
Znając wartość G
N
(
β
) i E
x
(
β
) można korzystając z wyrażenia (2.4)
określić wartość stosunku wiarygodności dla sygnału o nieznanej
fazie:
∫
∫
−
⋅
−
⋅
=
=
−
⋅
−
⋅
=
−
π
π
β
σ
α
β
σ
π
β
σ
α
β
σ
π
2
0
2
2
2
2
0
2
1
0
]
)
cos(
exp[
)
2
exp(
2
1
]
)
cos(
exp[
)
2
exp(
2
1
)
,...,
(
d
Z
E
d
Z
E
y
y
l
x
x
N
.
Wiedząc, że
)
(
2
1
0
2
0
)
cos(
u
I
d
e
u
∫
=
−
π
α
β
β
π
gdzie
)
(
0
u
I
jest zmodyfikowaną funkcją Bessela pierwszego rodzaju
zerowego rzędu (rys. 2.1) dostaje się ostateczne wyrażenie na
stosunek wiarygodności dla sygnału z nieznaną fazą:
)
(
)
2
exp(
)
,...,
(
2
0
2
1
0
σ
σ
Z
I
E
y
y
l
x
N
⋅
−
=
−
(2.9)
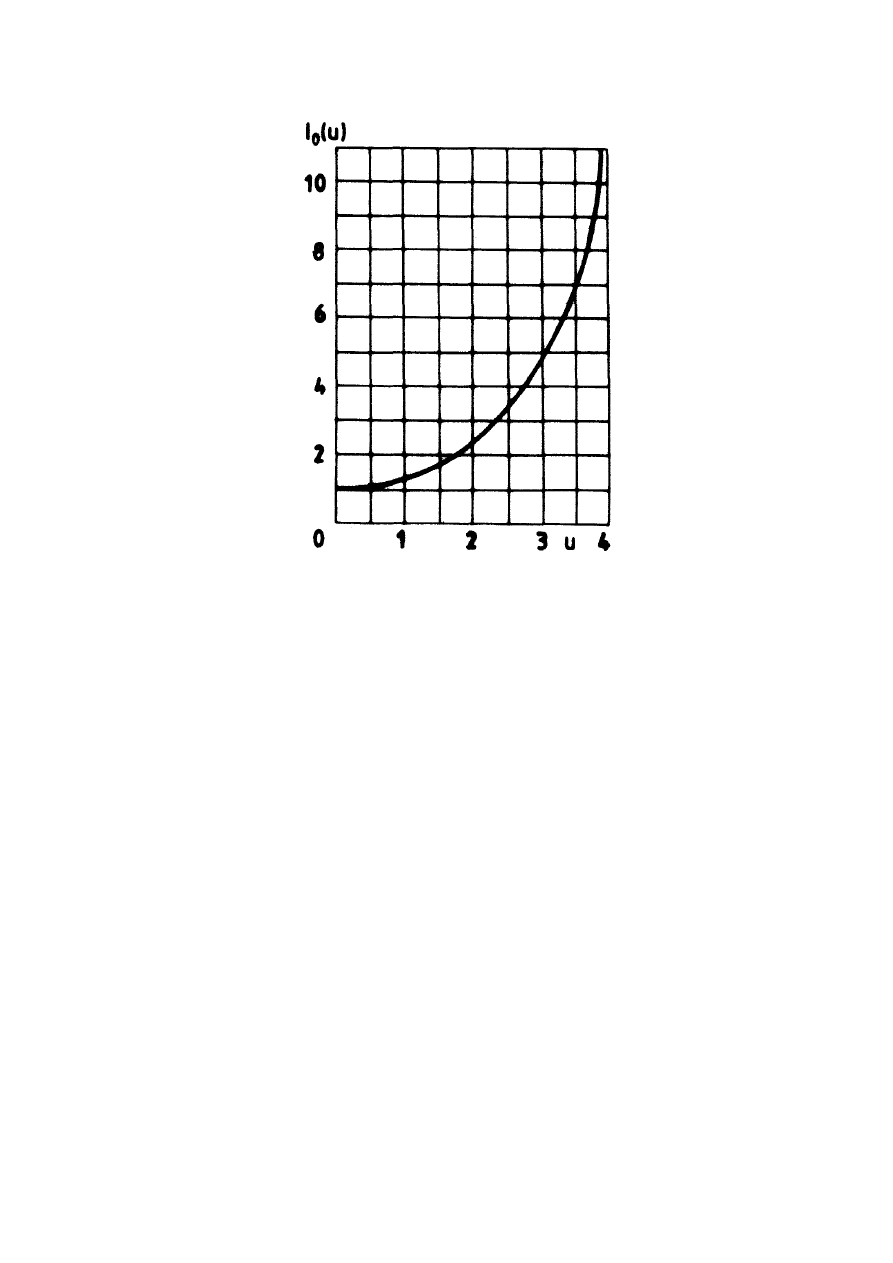
39
Rys. 2.1. Wykres zmodyfikowanej funkcji Bessela pierwszego rodzaju zerowego rzędu
Ponieważ zmodyfikowana funkcja Bessela pierwszego rodzaju
zerowego rzędu jest ściśle monotoniczna, to decyzję o obecności
sygnału x w przebiegu y można podejmować porównując wartość
statystyki Z z ustaloną wartością Z
0
. Jeśli Z<Z
0
, to przyjmuje się
prawdziwość hipotezy H
0
, zaś gdy Z>Z
0
, to wybierana jest hipoteza
H
1
. Wielkość Z
0
ustalana jest w zależności od porządanego przez
obserwatora poziomu prawdopodobieństwa fałszywego alarmu F.
Schemat blokowy urządzenia decyzyjnego działającego w oparciu o
statystykę Z jest pokazany na rysunku 2.2. Na układy mnożące
podaje się jako napięcia odniesienia dwa przebiegi kwadraturowe:
x
1
(n) oraz x
2
(n) (przesunięte względem siebie w fazie o
π
/2).
Istnienie dwóch kanałów kwadraturowych wyklucza możliwość straty
sygnału użytecznego na skutek nieznajomości jego fazy. Jeśli
przykładowo nie powoduje on wzrostu wartości z
1
wskutek
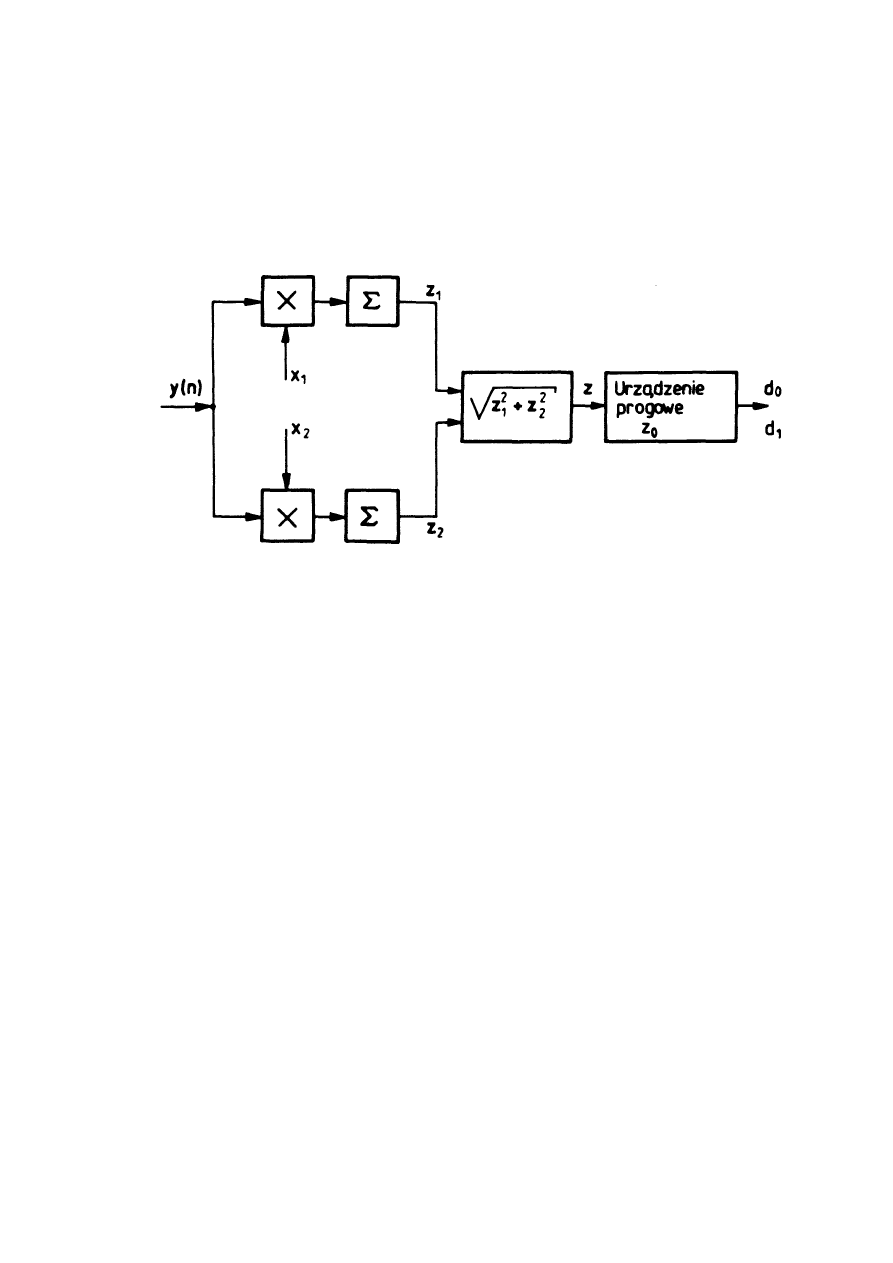
40
przesunięcia fazy o
π
/2 względem przebiegu odniesienia w
pierwszym kanale, to na pewno wywoła wzrost wartości z
2
w drugim
kanale. Jak widać, rezultat odbioru sygnału w detektorze z rysunku
2.2 nie zależy od przypadkowej fazy początkowej sygnału.
Rys. 2.2. Schemat blokowy układu decyzyjnego z dwoma kanałami kwadraturowymi
Układ, o którym przed chwilą była mowa jest optymalny jedynie,
gdy znany jest czas pojawienia się (opóźnienia) sygnału
użytecznego. Decyzja o istnieniu sygnału z nieznanym czasem
pojawienia się może być podjęta, jeśli sprawdzone zostaną hipotezy
o istnieniu tego sygnału w różnych momentach czasu. W ten sposób
dochodzi się do układu wielokanałowego, w którym każdy kanał ma
postać, jak na rys. 2.2, lecz “dostrojony” jest do innego czasu
opóźnienia. Odstępy między tymi czasami nie przekraczają
rozdzielczości odległościowej radaru, jakiej rzyczy sobie obserwator.
Schemat blokowy układu pokazany jest na rysunku 2.3. Takie
wielokanałowe układy mogą być użyte nie tylko dla sygnałów echa
różniących się czasem opóźnienia (odległość obiektu od radaru), ale
także częstotliwością nośną na skutek efektu Dopplera (prędkość
radialna obiektu względem radaru).
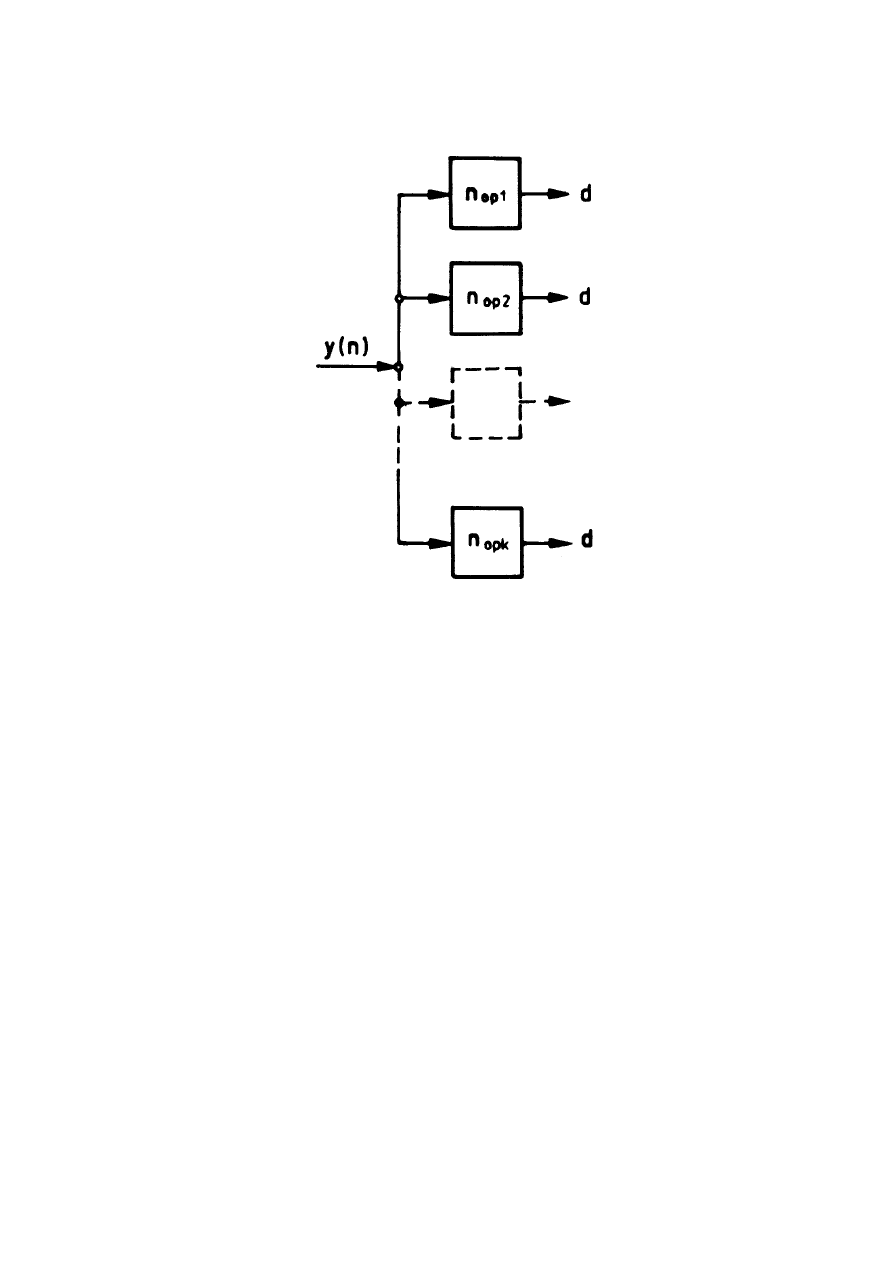
41
Rys. 2.3. Schemat blokowy wielokanałowego układu detekcyjnego dla różnych czasów
opóźnienia sygnału echa
2.4. ZASTOSOWANIE FILTRU DOPASOWANEGO W DETEKCJI
SYGNAŁÓW Z NIEZNANYM CZASEM OPÓŹNIENIA
W poprzednich punktach zostało pokazane, że decyzja o tym, która z
dwóch hipotez jest prawdziwa tzn.:
H
0
: y(t)=n(t)
−
odebrano tylko zakłócenia w postaci białego szumu o rozkładzie
Gaussa, lub
H
1
: y(t)=x(t)+n(t)
−
na tle wyżej wspomnianych zakłóceń odebrano sygnał echa
odbity od obiektu w powietrzu, podejmowana jest (ogólnie) przez porównanie
wartości stosunku wiarygodności
l
(y) z pewnym, ustalonym progiem
0
l .
Ponieważ stosunek wiarygodności jest funkcją monotoniczną, to wystarczy
porównywać wartość statystyki G
N
o postaci

42
∑
−
=
=
1
0
)
(
)
(
N
k
N
k
y
k
x
G
(2.10)
z progiem G
0
, jeśli detekuje się sygnały całkowicie znane, lub wartość statystyki
2
2
2
1
z
z
Z
+
=
w której
∑
∑
−
=
−
=
=
=
1
0
2
2
1
0
1
1
)
(
)
(
)
(
)
(
N
k
N
k
k
y
k
x
z
k
y
k
x
z
z progiem Z
0
, jeśli trzeba wykryć sygnał o nieznanej fazie. Czynniki y(k)=y(t=t
k
)
są dyskretnymi wartościami sygnału y(t) obserwowanego w przedziale czasu
t
∈〈
0;T
〉
. Budowa układu wielokanałowego z rys. 2.3, w którym każdy kanał
wykrywa sygnał o różnym czasie opóźnienia n
op
jest nieekonomiczna.
Statystykę G
N
(czy z
1
i z
2
) dla dowolnego n
op
byłoby wygodnie otrzymać
przepuszczając próbki sygnału y(n) przez jeden filtr liniowy. Filtr powinien
obliczać statystykę G
N
dla dowolnego czasu opóźnienia sygnału echa x(n),
który można zapisać jak poniżej:
−
≤
<
+
<
≤
+
≤
≤
=
1
,
0
0
)
(
)
(
1
1
N
n
N
n
n
n
dla
N
n
n
n
dla
n
u
n
x
op
op
op
op
(2.11)
Ciąg próbek u(n) reprezentuje sygnał echa z zerowym czasem opóźnienia.
Zakłada się, że postać ciągu jest znana. Korzystając z u(n) można zapisać
wyrażenie na statystykę G
N
poniższą zależnością:
∑
−
=
−
=
1
0
)
(
)
(
N
k
op
N
k
y
n
k
u
G
(2.12)
W celu uproszczenia analizy (ale bez skutków dla końcowych wniosków) można
przyjąć zerowy czas opóźnienia n
op
=0. Ponieważ sygnał x(n) jest różny od zera
tylko w pewnym przedziale, to można zmodyfikować sumę G
N
:
0
)
(
)
(
)
(
)
(
1
1
0
=
=
−
=
∑
∑
+
=
=
op
N
n
n
k
N
k
op
N
n
k
y
k
u
k
y
n
k
u
G
op
op
(2.13)
Sygnał na wyjściu filtru o skończonej odpowiedzi impulsowej (SOI) mającej
długość (N
1
+1) próbek jest opisany przez splot dyskretny:

43
∑
=
−
=
1
0
)
(
)
(
)
(
N
k
k
n
y
k
h
n
w
(2.14)
Wartość sygnału na wyjściu filtru w chwili N
1
wynosi:
∑
∑
=
=
−
=
−
=
1
1
0
0
1
1
1
)
(
)
(
)
(
)
(
)
(
N
k
N
k
k
y
k
N
h
k
N
y
k
h
N
w
(2.15)
Poszukiwany jest taki filtr, aby próbka na jego wyjściu w chwili N
1
była równa
wartości statystyki G
N
. Porównując powyższe wyrażenie z sumą na statystykę
G
N
(wyr. 2.13) dla sygnału z zerowym czasem opóźnienia, widać ,że:
∑
∑
=
=
=
−
=
−
1
1
0
1
0
1
)
(
)
(
)
(
)
(
)
(
)
(
N
k
N
k
k
u
k
N
h
dla
k
y
k
u
k
y
k
N
h
Wprowadzając nową zmienną n=N
1
-k otrzymuje się ostateczne wyrażenie na
odpowiedź impulsową filtru:
)
(
)
(
1
n
N
u
n
h
−
=
(2.16)
Filtr o takiej odpowiedzi impulsowej jest filtrem dopasowanym do sygnału
u(n). Jego odpowiedź impulsowa ma postać lustrzanego odbicia sygnału u(n)
względem chwili n=0 i przesunięta w prawo o N
1
, lub więcej próbek.
Przesunięcie nie może być jednak mniejsze od N
1
, ponieważ filtr będzie wtedy
nieprzyczynowy. Na wyjściu filtru będą pojawiać się opóźnione o N
1
próbek
wartości statystyki G
n
(lub z
1
czy z
2
, w zależności od tego, do jakiego sygnału
jest dopasowany filtr) dla kolejnych czasów opóźnienia n
op
. Im większe n
op
(czyli
większa odległość obiektu od radaru), tym później na wyjściu filtru pojawi się
wartość równa G
N
(n
op
).
2.5. ZASTOSOWANIE ZESPOLONYCH AMPLITUD W
ANALIZIE PROCESU DETEKCJI
Sygnał echa odbity od obiektu w powietrzu i docierający do stacji
radarowej ma postać sumy
)
(
)
(
)
(
t
n
t
x
t
y
+
=
gdzie x(t) jest sygnałem sinusoidalnym wielkiej częstotliwości, zaś n(t) szumem
białym, którego widmo obejmuje szeroki zakres. Jednakże w zagadnieniach
związanych z detekcją sygnałów o wąskim widmie w białych szumach można
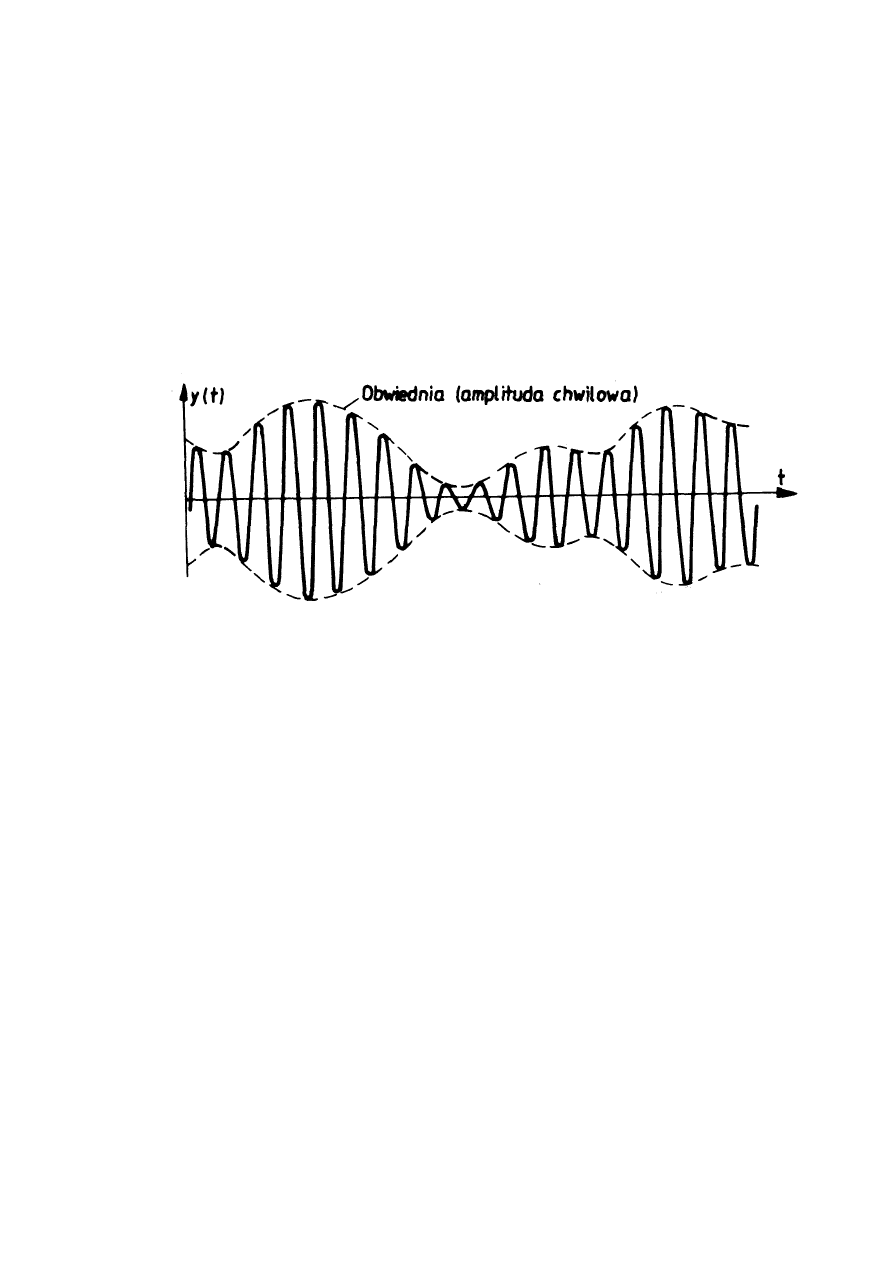
44
założyć, że sygnał i szum przechodzą przez filtr, którego pasmo przenoszenia
jest znacznie szersze niż widmo sygnału x(t). Zwykle rozważa się taki filtr jako
wąskopasmowy. Jego typ ma jednak niewielki wpływ na wykrywalność
sygnałów, ponieważ wycina on tylko składowe szumów z częstotliwościami nie
mającymi wpływu na sygnał użyteczny. Przebieg y(t) można traktować wtedy
jako wąskopasmowy tzn. jako przebieg sinusoidalny o częstotliwości takiej, jaką
ma x(t) i wolnozmiennej losowej aplitudzie i fazie [4]. Przykładowy szum
wąskopasmowy pokazano na poniższym wykresie 2.4.
Rys. 2.4. Przykładowy przebieg szumu wąskopasmowego
W przypadku sygnałów wąskopasmowych o wolnozmiennej amplitudzie i
fazie można znacznie uprościć analizę i obliczenia korzystając z pojęcia
sygnału analitycznego [2]. Niech dyskretny odpowiednik sygnału y(t) ma
poniższą postać:
)]
(
cos[
)
(
)
(
n
n
n
Y
n
y
y
ϕ
θ +
=
Tworzy się sygnał zespolony
ψ
y
(n), którego częścią rzeczywistą jest
y(n), zaś częścią urojoną transformata Hilberta sygnału y(n):
{ }
)
exp(
)
(
]
exp[
)]
(
exp[
)
(
)
(
)]
(
sin[
)
(
)]
(
cos[
)
(
)
(
)
(
)
(
θ
θ
ϕ
ψ
ϕ
θ
ϕ
θ
ψ
jn
n
jn
n
j
n
Y
n
n
n
n
jY
n
n
n
Y
n
y
jH
n
y
n
y
y
y
y
y
Y
=
=
+
+
+
=
+
=
)]
exp(
)
(
Re[
)
(
θ
jn
n
n
y
Y
=
.
Y(n) jest amplitudą chwilową (obwiednią) sygnału y(n), a Y(n) zespoloną
amplitudą zawierającą fazę
ϕ
y
(n):

45
)]
(
exp[
)
(
)
(
n
j
n
Y
n
y
ϕ
=
Y
.
Analogicznie można stworzyć sygnał analityczny i zespolone amplitudy dla
innych przebiegów. Niech sygnał x(n) będzie oczekiwanym sygnałem echa o
pewnym czasie opóźnienia n
op
:
)
(
)
(
op
n
n
u
n
x
−
=
(2.17)
)]
(
)
cos[(
)
(
)]
(
cos[
)
(
)
(
op
u
op
op
x
n
n
n
n
n
n
U
n
n
n
X
n
x
−
+
−
−
=
+
=
ϕ
θ
ϕ
θ
Po wprowadzeniu zespolonych amplitud dostaje się:
)]
exp(
)
exp(
)
(
Re[
)]
exp(
)
(
Re[
θ
θ
θ
jn
jn
n
n
jn
n
op
op
−
−
=
U
X
Ponieważ równość ta jest spełniona dla wszytkich wartości zmiennej
zespolonej exp(jn
θ
), to równe są także stojące przy tej zmiennej
współczynniki:
)
exp(
)
(
)
(
θ
op
op
jn
n
n
n
−
−
=
U
X
(2.18)
Analogicznie można zapisać zależności dla odpowiedzi impulsowej filtru
dopasowanego do sygnału u(n) o długości (N+1) próbek:
)
(
)
(
n
N
u
n
h
dop
−
=
(2.19)
Po wprowadzeniu zespolonych amplitud dostanie się że:
)]
exp(
)
exp(
)
(
Re[
)]
exp(
)
(
Re[
θ
θ
θ
jn
jN
n
N
jn
n
dop
−
−
=
U
H
Aby po prawej stronie powyższej równości znalazł się czynnik exp(jn
θ
), należy
wprowadzić wartość sprzężoną, co nie wpłynie na porównywanie części
rzeczywistych:
)]
exp(
)
exp(
)
(
Re[
)]
exp(
)
(
Re[
*
θ
θ
θ
jn
jN
n
N
jn
n
dop
−
−
=
U
H
Ponieważ równość jest spełniona dla wszystkich wartości exp(jn
θ
), to tak jak
poprzednio można zapisać:
)
exp(
)
(
)
(
*
θ
jN
n
N
n
dop
−
−
=
U
H
(2.20)
Powyższe wyrażenie określa związek między zespolonymi
amplitudami odpowiedzi impulsowej filtru dopasowanego i sygnału
oczekiwanego. Korzystając z zespolonych amplitud można zapisać
przebiegi na wejściu i wyjściu filtru dopasowanego:

46
∑
=
−
−
⋅
=
N
k
dop
dop
k
n
j
k
n
jk
k
jn
n
0
)]
)
(
exp(
)
(
Re[
)]
exp(
)
(
Re[
)]
exp(
)
(
Re[
θ
θ
θ
Y
H
W
(2.21)
W celu przekształcenia tej zależności zostanie wykorzystany
poniższy związek:
]
2
2
Re[
Re
Re
*
ab
ab
b
a
+
=
⋅
Jeśli ponadto uwzględnić, że część rzeczywista jest równa sumie
części rzeczywistych, to zależność opisującą filtrację sygnału można
zapisać jak dalej:
)]
exp(
))
(
)
(
Re[(
)]
)
(
exp(
)
(
)
exp(
)
(
2
1
)
)
(
exp(
)
(
)
exp(
)
(
2
1
Re[
)]
exp(
)
(
Re[
0
*
0
θ
θ
θ
θ
θ
θ
jn
n
n
k
n
j
k
n
jk
k
k
n
j
k
n
jk
k
jn
n
N
k
dop
N
k
dop
dop
2
1
W
W
Y
H
Y
H
W
+
=
=
−
−
−
+
+
−
−
=
=
∑
∑
=
=
(2.22)
gdzie:
)
2
)
(
exp(
)
(
)
(
2
1
)
(
)
(
)
(
2
1
)
(
0
*
0
θ
k
n
j
k
n
k
n
k
n
k
n
N
k
dop
N
k
dop
−
−
−
=
−
=
∑
∑
=
=
Y
H
W
Y
H
W
2
1
Porównując ze sobą zespolone amplitudy wychodzi, że:
)
(
)
(
)
(
n
n
n
dop
2
1
W
W
W
+
=
(2.23)
Jeżeli częstotliwość sygnału użytecznego
θ
jest dostatecznie duża w stosunku
do szerokości widma sygnału y(n), to amplitudy zespolone są funkcjami
wolnozmiennymi w stosunku do czynnika szybko zmieniającego się w czasie
exp(
−
jn2
θ
). Podczas sumowania zauważa się, że W
2
(n)<< W
1
(n) i można
składową W
2
(n) pominąć:
∑
=
−
=
≅
N
k
dop
dop
k
n
k
n
n
0
)
(
)
(
2
1
)
(
)
(
Y
H
W
W
1
(2.24)
Korzystając z wcześniejszego przedstawienia h
dop
(n) za pomocą u(n)
(wyrażenia 2.19 i 2.20) dostaje się, że:

47
∑
=
−
−
−
≅
N
k
dop
k
n
jN
k
N
n
0
*
)
(
)
exp(
)
(
2
1
)
(
Y
U
W
θ
(2.25)
Biorąc moduł zespolonej amplitudy W
dop
(n) otrzyma się wyrażenie na obwiednię
sygnału na wyjściu filtru dopasowanego:
∑
=
−
−
=
=
N
k
dop
dop
k
n
k
N
n
n
W
0
)
(
)
(
*
2
1
)
(
)
(
Y
U
W
(2.26)
Poczynione dotąd rozważania wraz z zależnościami z punktu 2.3 można
zastosować do zaprojektowania detektora z filtrem dopasowanym dla sygnałów
z nieznaną fazą. Decyzja odnośnie obecności sygnału echa radarowego będzie
podejmowana poprzez porównanie wartości statystyki Z i progu Z
0
określonego
przez poziom prawdopodobieństwa fałszywego alarmu F.
Wyrażenia na x
1
(n) oraz x
2
(n) z punktu 2.3 po wprowadzeniu zespolonych
amplitud można zapisać jak poniżej:
)]
exp(
)
(
*
Im[
)]
exp(
)
(
Im[
)]
(
sin[
)
(
)
(
)]
exp(
)
(
*
Re[
)]
exp(
)
(
Re[
)]
(
cos[
)
(
)
(
2
1
θ
θ
ϕ
θ
θ
θ
ϕ
θ
jn
n
jn
n
n
n
n
X
n
x
jn
n
jn
n
n
n
n
X
n
x
x
x
−
=
−
=
+
−
=
−
=
=
+
=
X
X
X
X
(2.27)
gdzie
)]
(
exp[
)
(
)
(
n
j
n
X
n
x
ϕ
=
X
Wobec powyższego wyrażenia na z
1
i z
2
z punktu 2.3 będą miały postać (sygnał
y(n) obserwowany jest w zakresie n od 0 do N
1
-1):
∑
∑
−
=
−
=
−
=
−
=
1
0
2
1
0
1
1
1
)]
exp(
)
(
*
)
(
Im[
)]
exp(
)
(
*
)
(
Re[
N
k
N
k
jk
k
k
y
z
jk
k
k
y
z
θ
θ
X
X
(2.28)
Wiedząc, że dla dowolnej liczby zespolonej a=Re[a]+jIm[a] słuszna jest
równość
(
) (
)
2
2
Im
Re
a
a
a
+
=
można zapisać wyrażenie na statystykę Z:
∑
−
=
−
=
+
=
1
0
2
2
2
1
1
)
exp(
)
(
*
)
(
N
k
jk
k
k
y
z
z
Z
θ
X
(2.29)
Wykorzystując następujący związek, że
)
exp(
)
(
*
2
1
)
exp(
)
(
2
1
)]
(
cos[
)
(
)
(
θ
θ
ϕ
θ
jn
n
jn
n
n
n
n
Y
n
y
y
−
+
=
+
=
Y
Y
48
uzyskuje się
∑
−
=
−
−
+
−
=
1
0
1
)
exp(
)
(
*
)
exp(
)
(
*
2
1
)
exp(
)
(
*
)
exp(
)
(
2
1
N
k
jk
k
jk
k
jk
k
jk
k
Z
θ
θ
θ
θ
X
Y
X
Y
Drugi czynnik jest szybkozmienny (z częstotliwością 2
θ
) w porównaniu do
pierwszego i podobnie jak poprzednio można go pominąć
∑
−
=
≅
1
0
1
)
(
*
)
(
2
1
N
k
k
k
Z
X
Y
(2.30)
Uwzględniając zależności (2.17) i (2.18), że x(n)=u(n-n
op
) dostaje się:
∑
−
=
−
≅
1
0
1
)
exp(
)
(
*
)
(
2
1
)
(
N
k
op
op
op
jn
n
k
k
n
Z
θ
U
Y
(2.31)
Po wyniesieniu przed sumę czynnika exp(jn
op
θ
) i uwzględnieniu, że jego moduł
równy jest jeden, ostatecznie wychodzi, że:
∑
−
=
−
≅
1
0
1
)
(
)
(
*
2
1
)
(
N
k
op
op
k
n
k
n
Z
Y
U
(2.32)
Ponieważ sygnał x(n) jest różny od zera tylko w pewnym fragmencie całego
przedziału obserwacji, to w sumie na Z(n
op
) wystarczy wziąć pod uwagę tylko
(N+1) próbek sygnału użytecznego tzn. od n
op
do n
op
+N:
∑
+
=
−
≅
N
n
n
k
op
op
op
op
k
n
k
n
Z
)
(
)
(
*
2
1
)
(
Y
U
(2.33)
Wartość obwiedni sygnału na wyjściu filtru dopasowanego (patrz wzór 2.26) w
chwili n=(N+n
op
) przedstawia poniższa zależność:
∑
∑
∑
=
=
=
−
=
+
−
−
=
=
−
+
−
=
+
=
+
N
k
op
N
k
op
N
k
op
op
dop
op
dop
k
n
k
k
k
n
N
N
k
n
N
k
N
n
N
n
N
W
0
0
0
)
(
)
(
*
2
1
)
(
)
(
*
2
1
)
(
)
(
*
2
1
)
(
)
(
Y
U
Y
U
Y
U
W
(2.34)
z której porównawszy wyrażenia objęte znakiem sumy z (2.33) widać, że:
)
(
)
(
op
op
dop
n
Z
n
N
W
=
+
(2.35)
tzn. amplituda chwilowa przebiegu na wyjściu filtru dopasowanego jest równa
wartości statystyki Z(n
op
) dla każdej wielkości czasu opóźnienia sygnału n
op
,
czyli inaczej: dla wszystkich odległości obiektu od stacji radarowej [5]. W ten
sposób dla utworzenia wielkości Z(n
op
) wystarczy jeden kanał z filtrem
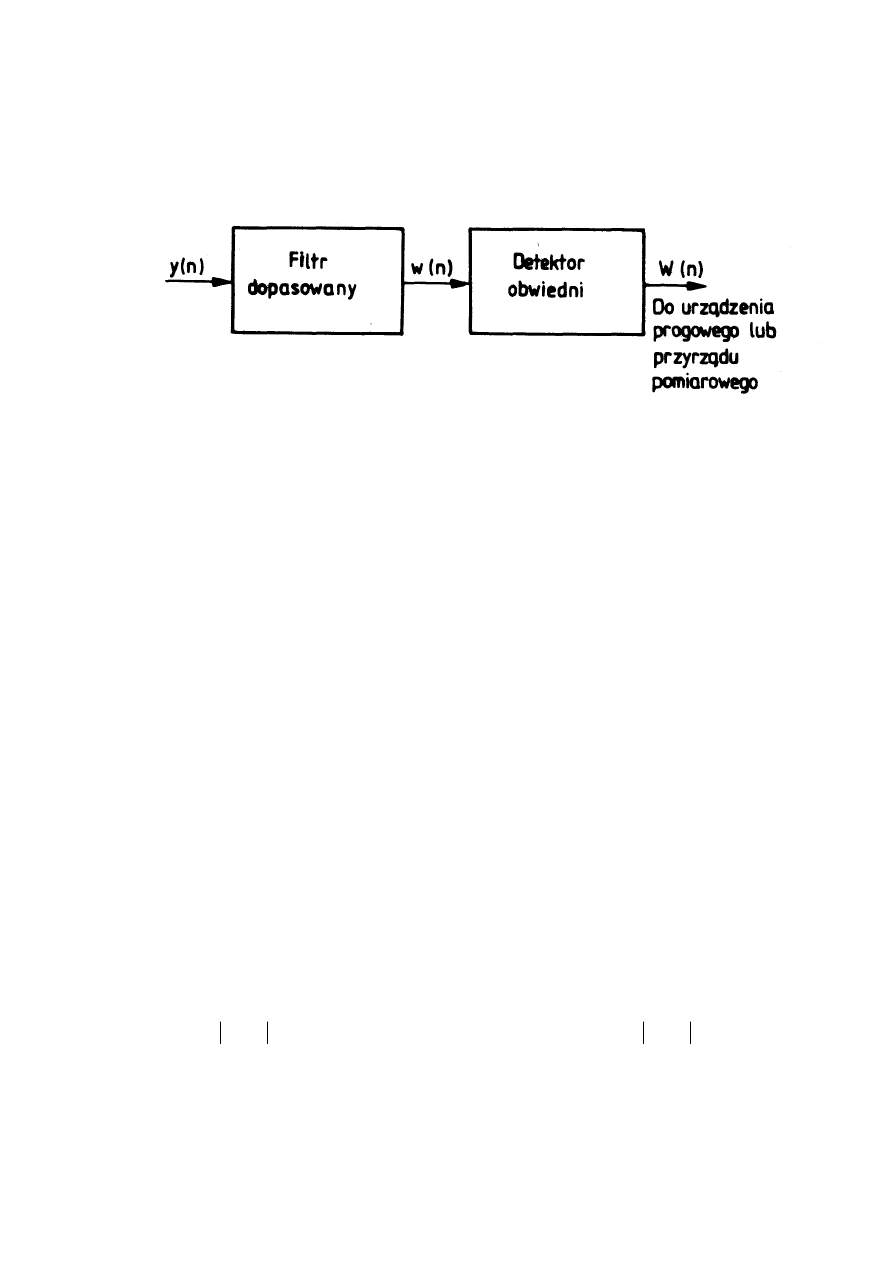
49
dopasowanym, zaś w celu uzyskania amplitudy sygnału na wyjściu filtru należy
użyć detektora obwiedni. Schemat blokowy takiego urządzenia pokazany jest
na rysunku 2.5 na następnej stronie.
Rys. 2.5. Schemat blokowy jednokanałowego detektora z filtrem dopasowanym dla sygnału o
nieznanej fazie
Pozostaje jeszcze znalezienie funkcji gęstości prawdopodobieństwa
statystyki Z(n
op
), czyli rozkład wartości przebiegu będącego obwiednią sygnału
na wyjściu filtru dopasowanego.
W przypadku, gdy prawdziwa jest hipoteza H
0
, to sygnał na wejściu filtru
składa się tylko z szumu białego gaussowskiego o zerowej wartości
oczekiwanej i wariancji
σ
2
. Przejście sygnału przez filtr liniowy nie zmienia typu
rozkładu, tak więc przebieg na wyjściu filtru dopasowanego również będzie
szumem gaussowskim (lecz już nie białym). Wartość oczekiwana pozostanie
zerowa, zaś zmieni się wariancja:
u
N
k
N
k
dop
w
E
k
N
u
k
h
w
D
2
0
2
2
0
2
2
2
2
)
(
)
(
]
[
σ
σ
σ
σ
=
−
=
=
=
∑
∑
=
=
gdzie E
u
jest energią sygnału użytecznego. Obwiednia sygnału w(n) za filtrem i
jej rozkład prawdopodobieństwa zostanie wyznaczony z wykorzystaniem
pojęcia sygnału analitycznego. Sygnał analityczny skojarzony z przebiegiem
w(n) ma postać:
)}
(
{
)
(
)
(
n
w
jH
n
w
n
w
+
=
ψ
Krzywa
)
(
)
(
n
Z
n
w
=
ψ
będzie poszukiwaną obwiednią, a
))
(
(
)
)
(
(
0
n
Z
p
n
p
w
=
ψ
poszukiwaną gęstością prawdopodobieństwa obwiedni. Z własności sygnału
analitycznego wynika, że zmienne losowe w(n) i H{w(n)} są nieskorelowane dla
danego n. Poza tym ponieważ H{w(n)} otrzymuje się w wyniku liniowej operacji

50
nad w(n
op
), to musi mieć taki sam rozkład, czyli rozkład Gaussa. W
szczególności widmo mocy i wariancja obu przebiegów będą jednakowe.
Skoro tak, to łączny rozkład gęstości prawdopodobieństwa zmiennych
losowych: w i H{w} można zapisać poniższym wyrażeniem
)
2
exp(
2
1
)
2
]
[
exp(
2
1
])
[
(
)
(
])
[
,
(
2
2
2
2
2
2
2
w
w
w
w
Z
w
H
w
w
H
p
w
p
w
H
w
p
σ
πσ
σ
πσ
−
=
+
−
=
=
. (2.36)
Poszukiwany jest rozkład zmiennej losowej
]
[
2
2
w
H
w
Z
+
=
dla Z
≥
0. Dystrybuanta zmiennej losowej Z równa jest masie
prawdopodobieństwa na obszarze będącym kołem o promieniu Z:
∫∫
≤
+
=
Z
w
H
w
w
H
w
Z
w
dwdH
w
H
w
p
Z
F
]
[
]
[
,
2
2
]
[
])
[
,
(
)
(
Przechodząc na współrzędne biegunowe
β
β
sin
]
[
cos
r
w
H
r
w
≡
≡
wychodzi, że
∫
∫
∫
−
−
=
−
=
=
=
Z
w
w
w
Z
w
H
w
Z
Z
dr
r
r
dr
r
J
r
p
d
Z
F
0
2
2
2
2
2
0
]
[
,
2
0
)
2
exp(
1
)
2
exp(
2
2
1
]
,
[
)
,
(
)
(
σ
σ
π
πσ
β
β
β
π
(2.37)
Po zróżniczkowaniu uzyskanego wyrażenia na F
Z
(Z) dostaje się wyrażenie na
gęstość prawdopodobieństwa statystyki Z w przypadku prawdziwości hipotezy
H
0
, czyli tzw. rozkład Rayleigha [9]:
0
),
2
exp(
)
(
2
2
2
0
≥
−
=
Z
Z
Z
Z
p
w
w
σ
σ
(2.38)
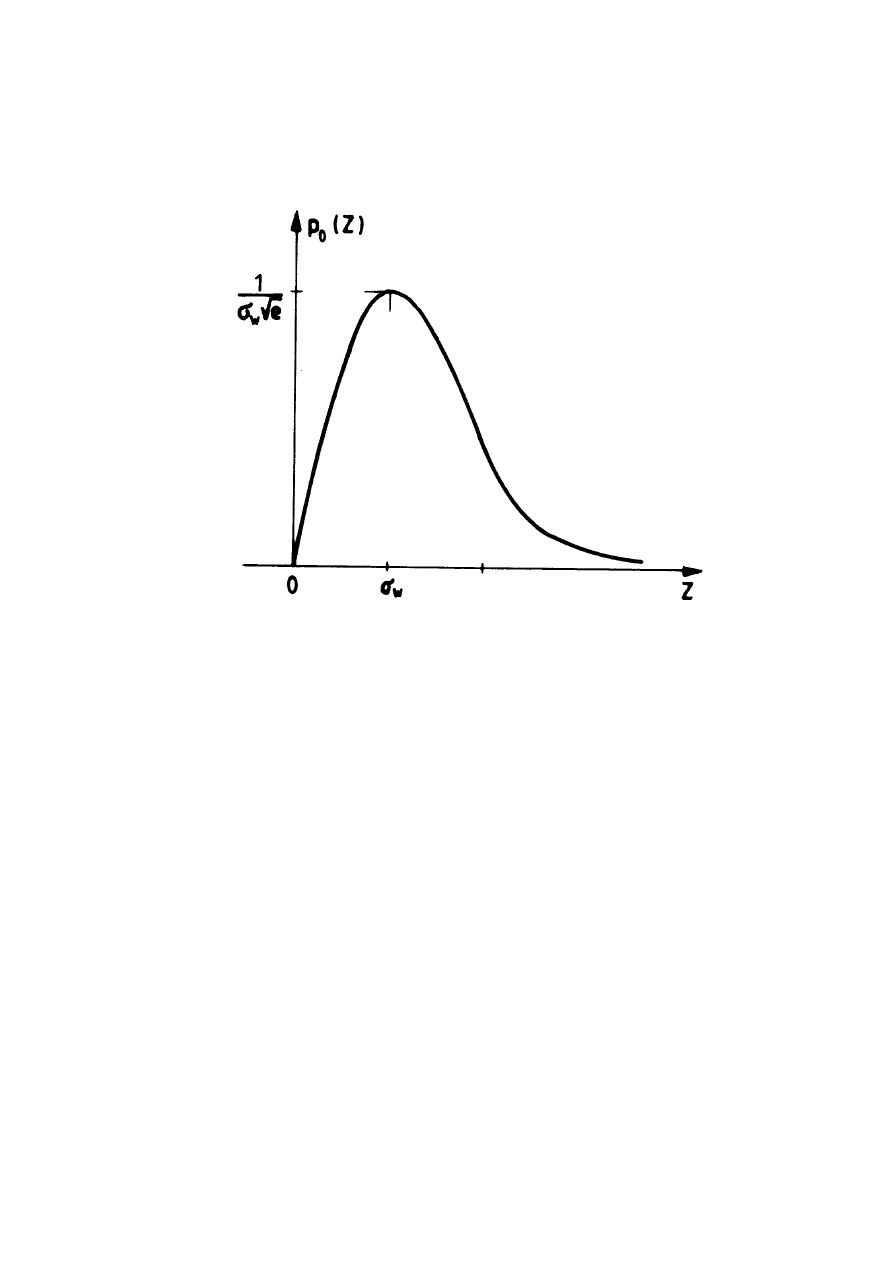
51
Krzywa rozkładu Rayleigha pokazana jest na wykresie 2.6 na kolejnej stronie.
Rys. 2.6. Gęstość prawdopodobieństwa obwiedni szumu wąskopasmowego czyli tzw. rozkład
Rayleya.
σ
w
jest odchyleniem standardowym szumu
W przypadku, kiedy prawdziwa jest hipoteza H
1
, to sygnał na wejściu filtru
dopasowanego składa się z sygnału echa oraz addytywnego szumu białego
gaussowskiego o zerowej wartości oczekiwanej i wariancji
σ
2
. Na wyjściu filtru
pojawi się sygnał będący sumą szumu takiego, jak w przypadku prawdziwości
hipotezy H
0
i przefiltrowanego sygnału użytecznego. Aby wyznaczyć rozkład
p
1
(Z(n)) należy (jak na początku niniejszego punktu 2.5) potraktować zakłócenia
na wyjściu filtru dopasowanego jako szum wąskopasmowy, o częstotliwości
nośnej
θ
. Skoro tak, to można go zapisać poniższym wyrażeniem:
)
sin(
)
(
)
cos(
)
(
))
(
cos(
)
(
θ
θ
ϕ
θ
n
n
n
n
n
n
n
n
n
N
s
c
n
w
−
=
+
(2.39)
gdzie

52
)
(
)
(
]
[
)
(
)
(
2
2
2
2
n
n
n
n
w
H
w
n
n
N
s
c
w
w
+
=
+
=
= ψ
)
)
(
)
(
(
tg
)
(
n
n
n
n
ac
n
c
s
n
=
ϕ
Sygnał wypadkowy na wyjściu filtru można przedstawić jako sumę prawej
strony wyrażenia (2.39) i Acos(n
θ
) [6]:
)
sin(
)
(
)
cos(
)
(
)
cos(
))
(
cos(
)
(
θ
θ
θ
ϕ
θ
n
n
n
n
n
n
n
A
n
n
n
W
s
c
w
−
+
=
+
(2.40)
Początek obserwacji przebiegu (2.40) przyjęto tak, aby faza była równa zero i
wtedy składnik użyteczny ma postać Acos(n
θ
). Ponieważ (2.40) reprezentuje
sygnał na wyjściu filtru dopasowanego, to wartość A nie jest amplitudą echa
radarowego x(n). W szczególności jeśli x(n)=u(n-n
op
), to składnik użyteczny na
wyjściu filtru dopasowanego o długości (N+1) próbek w chwili n=(N+n
op
) będzie
równy energii sygnału u(n):
∑
∑
∑
=
=
=
=
=
−
+
−
=
−
+
=
+
N
k
u
N
k
N
k
op
op
dop
op
u
E
k
u
k
n
N
u
k
N
u
k
n
N
u
k
h
n
N
w
0
2
0
0
)
(
)
(
)
(
)
(
)
(
)
(
Porównując stronami wyrażenie (2.40) wychodzi, że:
)
(
))
(
sin(
)
(
)
(
)
(
))
(
cos(
)
(
)
(
1
1
n
n
n
n
W
n
n
A
n
n
A
n
n
W
n
n
s
w
s
c
w
c
=
=
−
=
−
=
ϕ
ϕ
(2.41)
Poszukiwany jest rozkład obwiedni sygnału za filtrem, czyli W(n), gdzie:
2
2
s
c
n
n
W
+
=
i W
≥
0. Podstawiając (2.41) do wyrażenia o postaci (2.36) otrzymuje się:
)
2
)
(
exp(
2
1
)
2
exp(
2
1
)
,
(
2
2
1
2
1
2
2
2
2
2
1
1
,
w
s
c
w
w
s
c
w
s
c
ns
nc
n
A
n
n
n
n
n
p
σ
πσ
σ
πσ
+
−
−
=
+
−
=
(2.42)
Gęstość prawdopodobieństwa zmiennej W: p
W
(W) można wyliczyć albo
różniczkując jej dystrybuantę F
W
(W), albo z poniższej zależności:
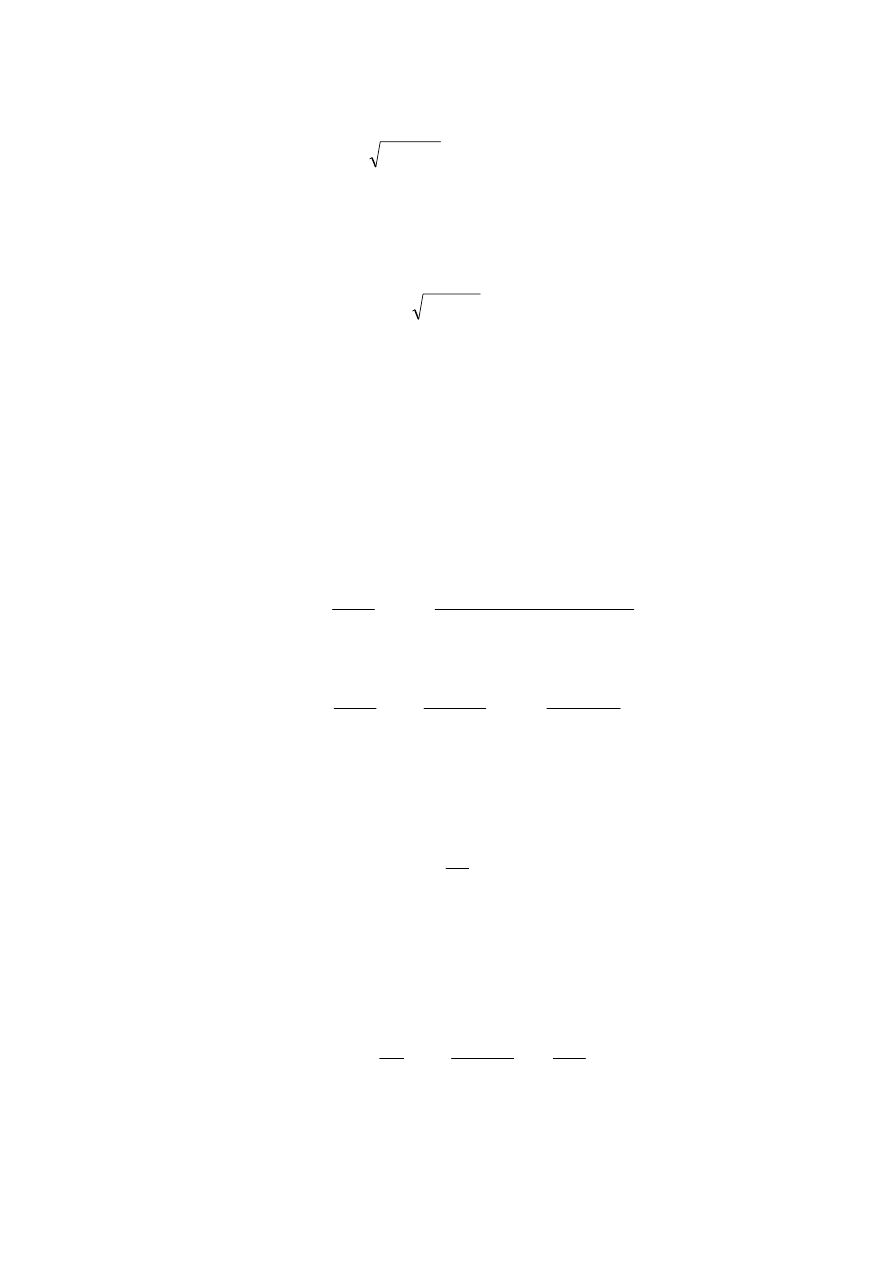
53
1
1
1
1
,
2
1
2
1
)
,
(
)
(
)
(
s
c
D
s
c
ns
nc
s
c
W
dn
n
d
n
n
p
dW
W
n
n
W
P
dW
W
p
∫∫
∆
=
+
<
+
<
=
gdzie
∆
D jest obszarem płaszczyzny n
c1
,n
s1
takim, że dla W
≥
0
dW
W
n
n
W
s
c
+
<
+
<
2
1
2
1
Obszar ten jest pierścieniem kołowym o wewnętrznym promieniu W i
zewnętrznym W+dW. Wprowadzając współrzędne biegunowe
β
β
β
WdWd
dn
dn
W
n
W
n
s
c
s
c
≡
≡
≡
1
1
1
1
sin
cos
dostaje się:
∫
+
−
−
=
π
β
σ
β
β
πσ
2
0
2
2
2
2
)
2
)
sin
(
)
cos
(
exp(
2
1
)
(
WdWd
W
A
W
dW
W
p
w
w
W
a więc
β
σ
β
σ
πσ
π
d
AW
A
W
W
W
p
w
w
w
W
)
cos
exp(
)
2
exp(
2
)
(
2
0
2
2
2
2
2
∫
⋅
+
−
=
(2.43)
Ostatnią całkę można wyrazić przez zmodyfikowaną funkcją Bessela rzędu
zerowego:
∫
=
π
β
β
π
2
0
cos
0
2
1
)
(
d
e
x
I
x
i ostatecznie rozkład prawdopodobieństwa obwiedni sygnału (czyli rozkład
statystyki Z) na wyjściu filtru dopasowanego przy prawdziwości hipotezy H
1
(tzw. rozkład Rice’a) ma poniższą postać:
0
),
(
)
2
exp(
)
(
2
0
2
2
2
2
1
≥
⋅
+
−
=
Z
ZE
I
E
Z
Z
Z
p
w
u
w
u
w
σ
σ
σ
(2.44)
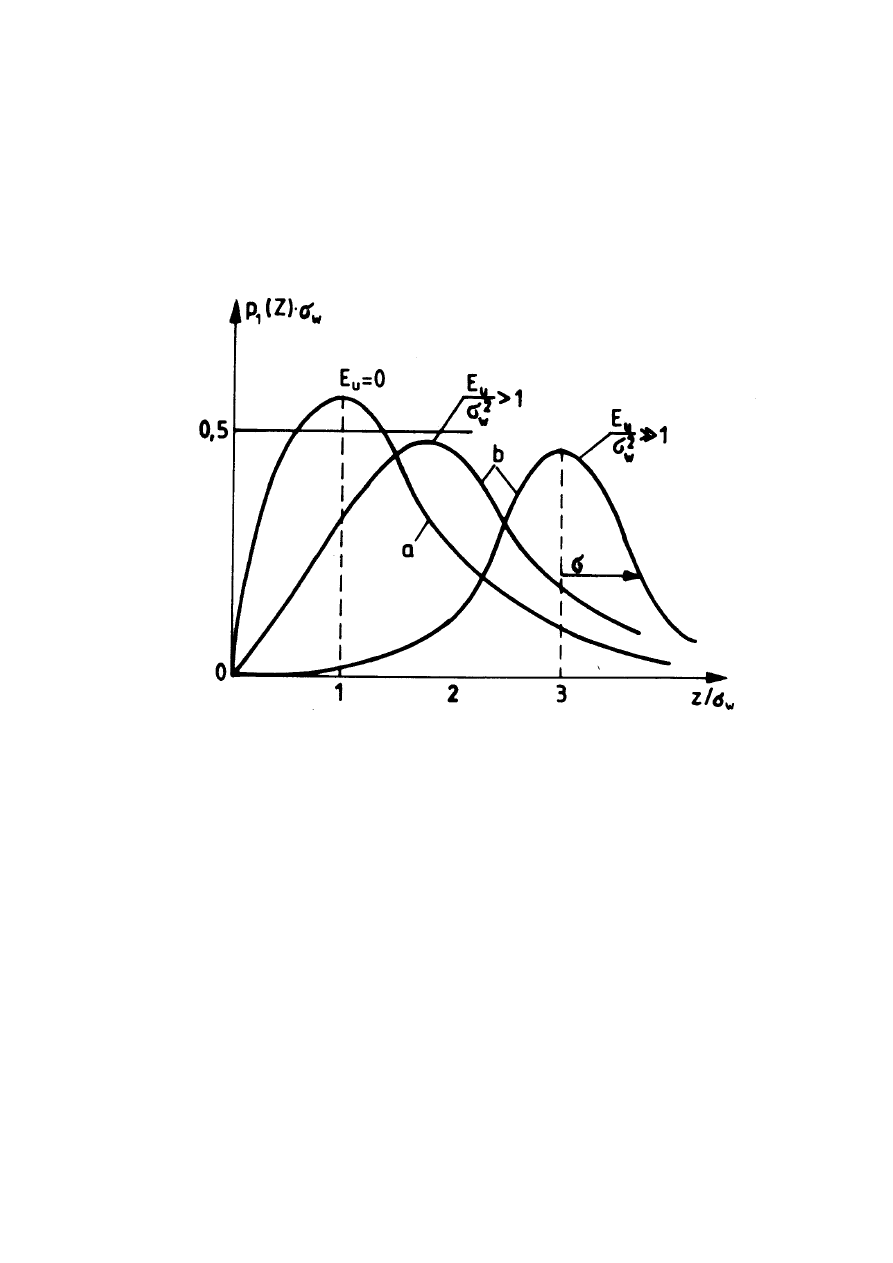
54
Krzywe rozkładu Rice’a dla różnych wartości energii sygnału użytecznego E
u
pokazane są na następnej stronie na wykresie 2.7.
Rys. 2.7. Gęstość prawdopodobieństwa obwiedni sumy sygnału i szumu wąskopasmowego
czyli tzw. rozkład Rice’a dla różnych wartości stosunku sygnału do szumu:
a
−
rozkład Rayleya
b
−
rozkład Rice’a
3. INTEGRACJA IMPULSÓW I STABILIZACJA
POZIOMU FAŁSZYWEGO ALARMU
55
3.1. ZASADA DZIAŁANIA RZECZYWISTYCH SYSTEMÓW
RADIOLOKACYJNYCH
W poprzednich rozdziałach opisano podstawy detekcji oraz przedstawiono
sytuację, w której do wykrywania obiektów w przestrzeni wykorzystuje się tylko
jeden sygnał echa. Przebieg wejściowy był obserwowany tylko w pojedynczym
przedziale czasu 0
<
t
<
T, w którym sygnał echa występował lub nie istniał.
Odpowiada to przypadkowi, gdy obserwator nakierowuje antenę radaru na jakiś
wybrany wycinek przestrzeni i w jego kierunku wysyła jeden impuls.
W wykorzystywanych rzeczywistych urządzeniach radiolokacyjnych
można nadawać wiele impulsów w kierunku obiektu i obserwować pewną liczbę
przedziałów, a w każdym z nich oczekiwać sygnału echa, jeśli tylko cel
rzeczywiście istnieje. Antena radaru obraca się ze stałą prędkością kątową i
analizuje otaczającą przestrzeń specjalnie ukształtowaną wiązką sondującą.
Przykład takiej wiązki jest pokazany na rysunku 3.1.
Rys. 3.1. Przykładowa wiązka radarowa (modulowana charakterystyką anteny) skanująca
przestrzeń dookoła stacji radiolokacyjnej
Stacja radarowa co pewien stały interwał czasowy generuje sygnał w postaci
impulsu wielkiej częstotliwości s
0
(t). Charakterystyka promieniowania anteny w
kierunku obiektu (przedstawiona na rys 3.1) jest określona pewną funkcją czasu
H
1
(t). Tak więc sygnał sondujący promieniowany w kierunku obiektu jest
opisany przez iloczyn H
1
(t)s
0
(t). Natężenie pola sygnału echa odbitego od
obiektu i przychodzącego do stacji radarowej z opóźnieniem t
op
wynosi z
dokładnością do stałej H
1
(t-t
op
)s
0
(t-t
op
), gdzie

56
c
r
t
op
2
=
,
przy czym r jest odległością celu od stacji, a c szybkością
rozchodzenia się fal elektromagnetycznych (czyli prędkością
światła).
W rezultacie ruchu anteny odbiorczej jej charakterystyka jest także funkcją
czasu. Oznaczona zostanie przez H
2
(t). Sygnał użyteczny x(t) przychodzący na
wejście odbiornika jest modulowany dodatkowo funkcją H
2
(t) i może być
zapisany w postaci:
)
(
)
(
)
(
)
(
0
2
1
op
op
op
t
t
s
t
t
H
t
t
H
t
x
−
⋅
−
⋅
−
=
Dla typowych jednoantenowych radiolokatorów H
1
(t)=H
2
(t)=H(t). Równocześnie
zmiana charakterystyki antenowej H(t) w czasie t
op
jest tak znikoma, że można
ją zaniedbać [5], a tym samym
)
(
)
(
)
(
0
2
op
t
t
s
t
H
t
x
−
⋅
=
Tak więc radiolokacyjny sygnał echa pochodzący od obiektu jest
modulowanym przebiegiem wielkiej częstotoliwości x(t), przy czym
modulacja ta jest wynikiem nie tylko celowego działania
obserwatora, ale i charakterystyki anteny nadawczo-odbiorczej.
Modulacja ta w ustalonych warunkach pracy radaru nie ulega
zmianie.
Modulowany, pojedynczy sygnał wielkiej częstotliwości x(t)
można zapisać w postaci
))
(
cos(
)
(
)
(
t
t
t
X
t
x
x
ϕ
ω +
=
(3.1)
Sygnał taki, oraz powyższy zapis wykorzystywane były w analizie
detekcji w poprzednim rozdziale. W zapisie tym
ω
jest pulsacją
nośną, zaś X(t) i
ϕ
x
(t) funkcjami wolnozmiennymi w stosunku do
cos(
ω
t) określającymi amplitudową i fazową modulację sygnału
echa. Rysunek 3.2 na następnej stronie pokazuje kształt takiego
impulsu, jego obwiednię X(t), oraz przebieg fazy początkowej
ϕ
x
(t).
Ponieważ nie występuje modulacja fazy, to
ϕ
x
(t)=const.
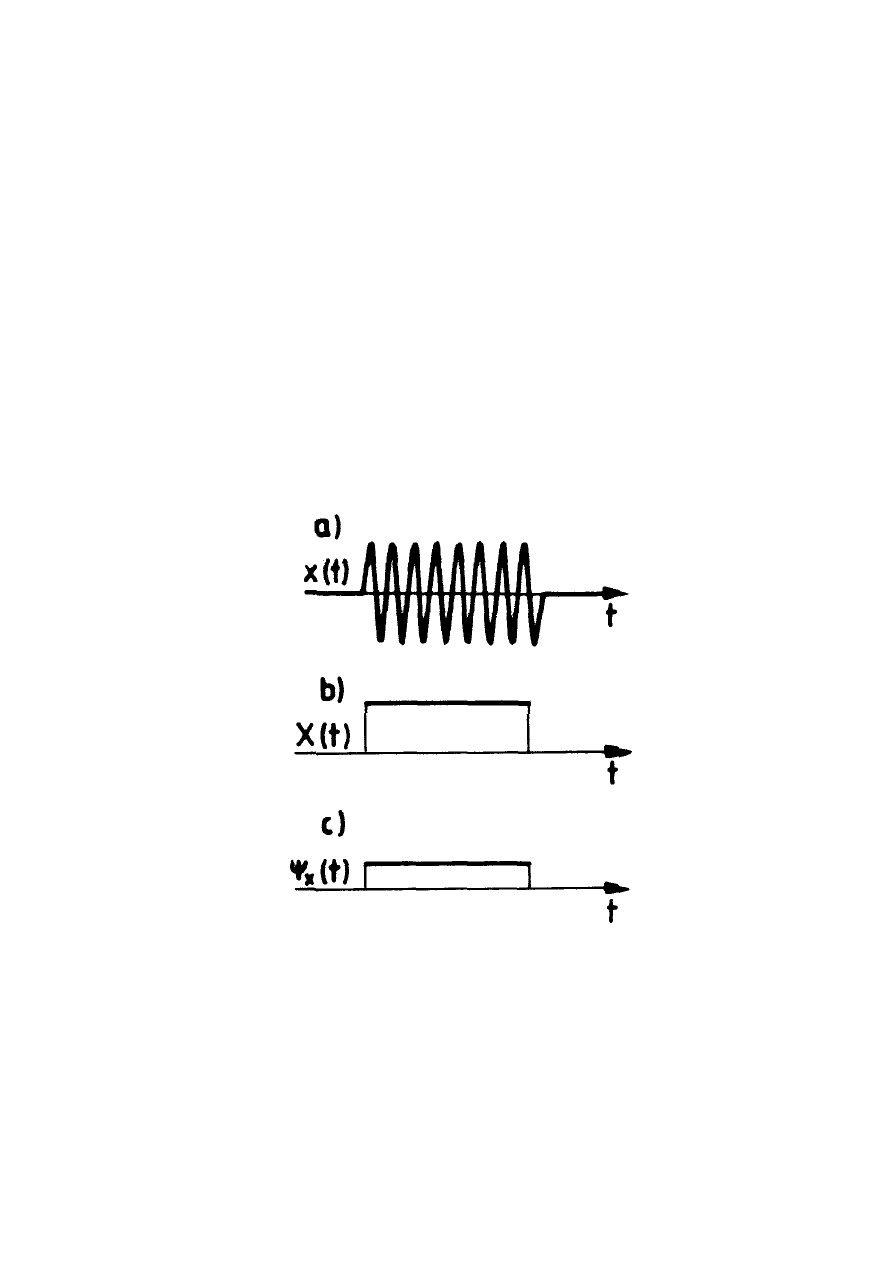
57
Na kolejnym rysunku 3.3 przedstawiono sygnał echa w postaci
paczki impulsów wielkiej częstotliwości, modulowanej
charakterystyką jednostajnie obracającej się anteny. Można go
zapisać jako sumę wyrażeń typu (3.1):
∑
+
=
i
i
i
t
t
t
X
t
x
))
(
cos(
)
(
)
(
ϕ
ω
(3.2)
Rysunek 3.3b przedstawia obwiednię paczki, zaś 3.3c przebieg fazy
początkowej jako funkcję czasu.
Rys. 3.2. Przykład impulsu wielkiej częstotliwości (a), jego obwiedni (b) oraz przebieg fazy
początkowej (c) w funkcji czasu
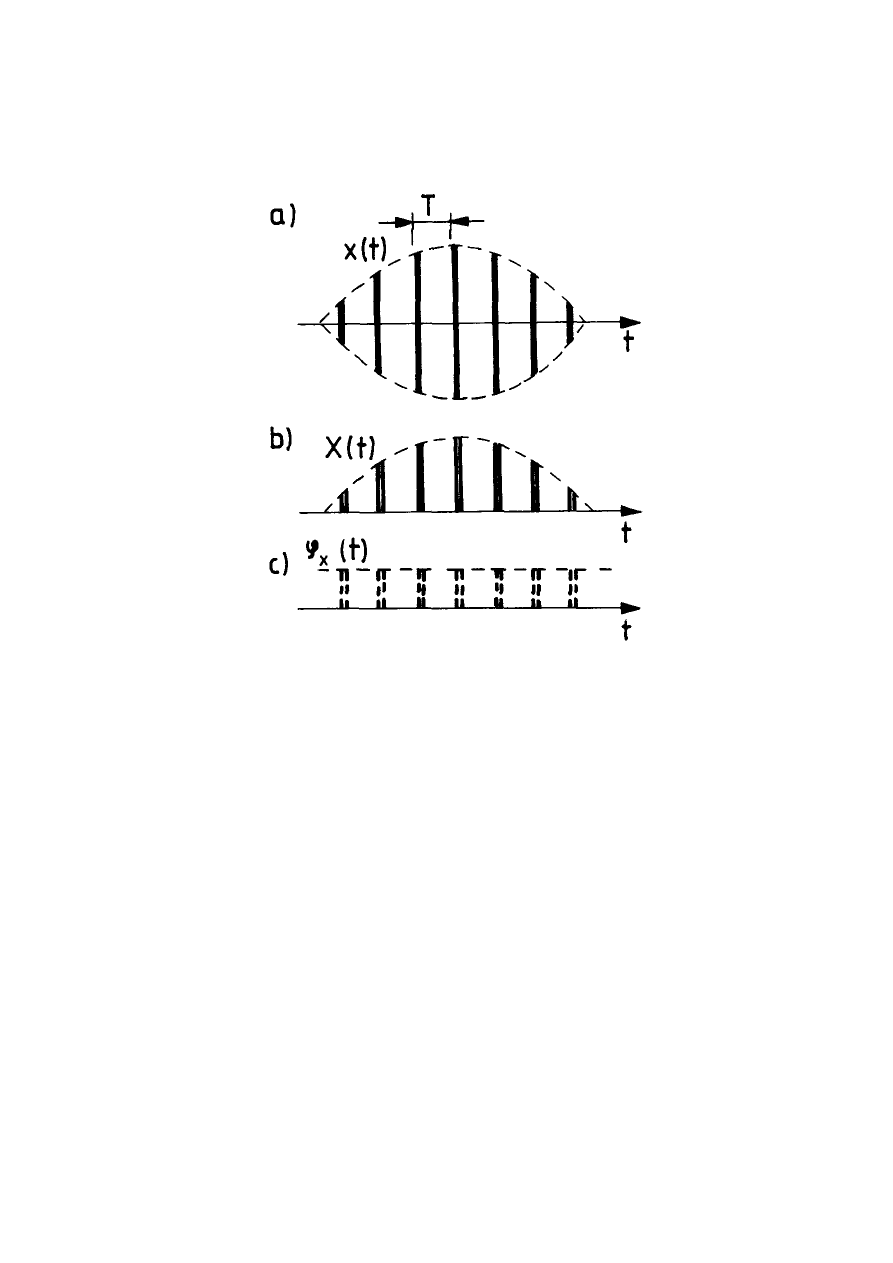
58
Rys. 3.3. Koherentna paczka impulsów echa modulowana charakterystyką anteny (a), jej
obwiednia (b) oraz przebieg fazy początkowej (c) w funkcji czasu dla nieruchomego obiektu
Jak widać z wykresu fazy, paczka jest echem odbitym od obiektu
nieruchomego, a impulsy są generowane przez nadajnik z taką
samą fazą początkową. Taka paczka, z jednoznacznie określonym
przebiegiem fazy
ϕ
x
(t) dla każdego impulsu nosi nazwę paczki
koherentnej.
Inaczej wygląda sytuacja, gdy nadajnik generuje impulsy w.cz.
z przypadkową fazą początkową. Jeśli w chwili nadawania fazy nie
zostaną zapamiętane, tak aby umożliwić późniejszą korektę w
sygnale echa, to w paczkach sygnałów odbieranych trzeba
traktować je jako przypadkowe i z góry nieznane. Paczka taka

59
zwana jest paczką niekocherentną. Można ją zapisać wyrażeniem
(3.3):
∑
+
+
=
i
i
i
i
t
t
t
X
t
x
)
)
(
cos(
)
(
)
(
β
ϕ
ω
(3.3)
W wyrażeniu tym parametr
β
i
jest zmienną losową o rozkładzie
równomiernym w przedziale od 0 do 2
π
(punkty 2.1-2.3, rozdz. 2),
przy czym dla każdego impulsu zmienne te są niezależne od
zmiennych losowych z innych impulsów.
W związku z tym, że antena radaru obraca się nieprzerwanie i
co pewien okres czasu (czyli co obrót o jakiś ułamek kąta pełnego)
emituje w przestrzeń wokół siebie impuls sondujący, obszar
powietrzny otaczający stację radarową po jednym obrocie anteny o
pełny kąt może być przedstawiony jako wykres trójwymiarowy. Na
jednej z osi będzie kąt azymutalny
α
w zakresie od 0 do 360 stopni,
na drugiej zasięg radaru od 0 do r
max
, zaś na osi pionowej moc
odebranego sygnału wraz z zakłóceniami. Zgodnie z teorią z
rozdziałów pierwszego i drugiego jeśli moc sygnału przekroczy
ustalony próg, to znaczy, że gdzieś tam w powietrzu znajduje się
cel. Ponieważ stacja jest w stanie emitować impulsy tak często, że
nawet dla szybko lecącego obiektu duża ich liczba trafi weń i odbije
się od niego przy niewielkiej zmianie jego położenia, to można
zwiększyć prawdopodobieństwo detekcji poprzez podejmowanie
decyzji na podstawie większej niż jeden liczby impulsów.
Urządzenie takie, zwane integratorem będzie wykonywać różne
operacje na impulsach, a następnie na podstawie uzyskanych z
impulsów wartości (na przykład średnia arytmetyczna) poprzez
porównanie ich z pewnym progiem będzie podejmować decyzję
odnośnie obecności obiektu w przestrzeni. Najprostszy taki
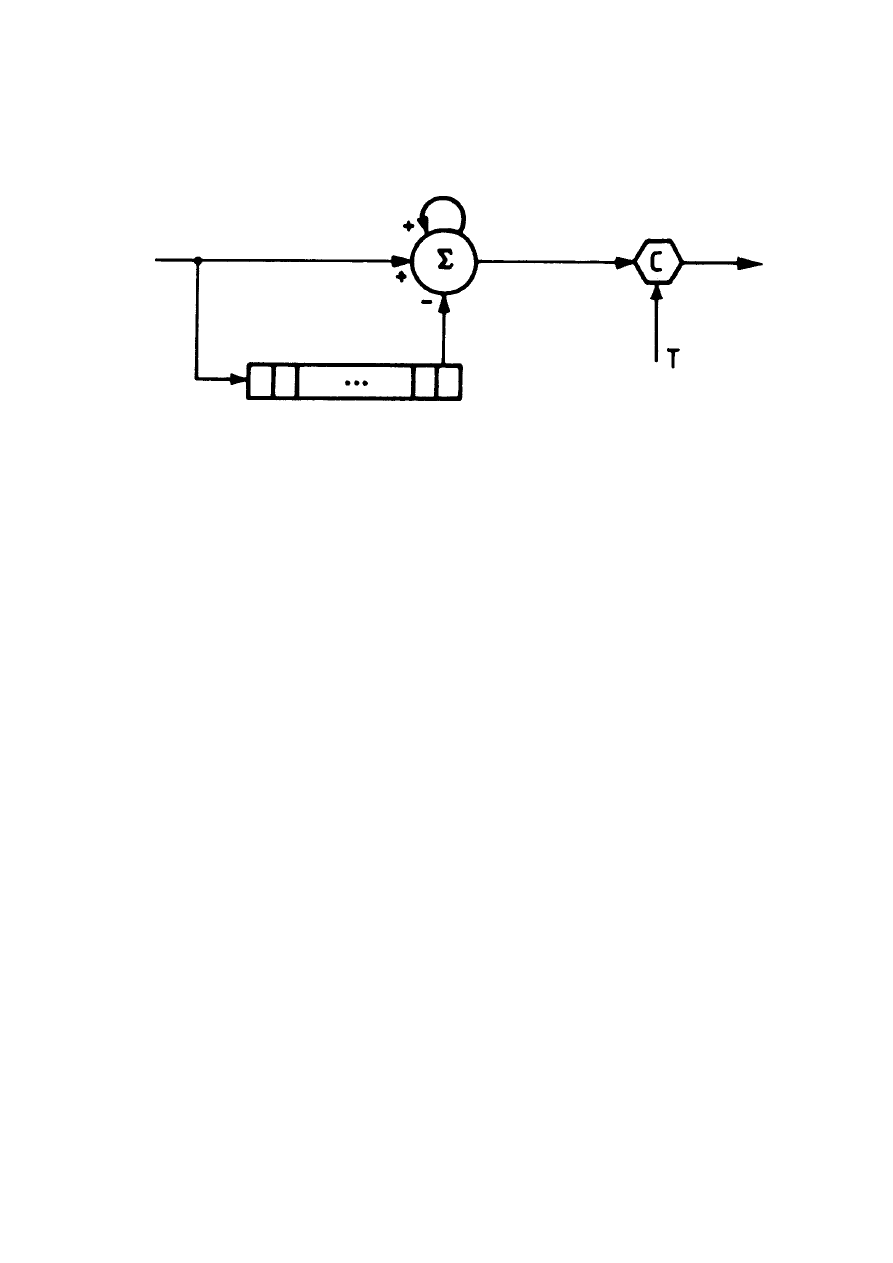
60
detektor/integrator typu “ruchome okno” ma strukturę pokazaną na
rysunku 3.4 [11].
Rys. 3.4. Schemat blokowy integratora typu „ruchowe okno”. ‘C’ oznacza porównywanie z
progiem decyzyjnym T
Jego działanie polega na sumowaniu ustalonej przez
obserwatora liczby
I
impulsów dla każdej komórki odległościowej.
Suma ostatnich
I
impulsów jest następnie porównywana z pewnym
progiem. Jeśli suma przekroczy próg, to znaczy, że w wycinku
obszaru, w którym wyemitowano te
I
impulsów znajduje się cel.
Działanie integratora ze schematu 3.4 opisuje poniższe wyrażenie:
I
i
i
i
i
x
x
S
S
−
−
−
+
=
1
(3.4)
gdzie S
i
oznacza sumę wartości ostatnich
i
impulsów, a x
i
wartość
i
-tego impulsu. Realizuje on zatem “kroczącą” sumę amplitud
I
impulsów, dzięki czemu w ramach całej paczki następuje narastanie
wartości sygnału wyjściowego. Jednocześnie szum, jako sygnał
przypadkowy nie ulega tak efektywnemu sumowaniu, co prowadzi
do poprawy stosunku sygnału do szumu na wyjściu integratora.
Punktem wyjścia do analizy działania integratora i wykrywania
będzie tak, jak dla pojedynczego impulsu, stosunek wiarygodności.

61
3.2. STOSUNEK WIARYGODNOŚCI DLA SYGNAŁU W POSTACI
PACZKI IMPULSÓW W.CZ. O NIEZNANYCH FAZACH
Dyskretny odpowiednik sygnału w postaci paczki impulsów wielkiej
częstotliwości z przypadkowymi fazami początkowymi można zapisać
poniższym wyrażeniem:
∑
+
+
=
i
i
i
i
n
n
n
X
n
x
]
)
(
cos[
)
(
,...)
,
,
(
1
0
β
ϕ
θ
β
β
(3.5)
Amplitudy impulsów są wielkościami zdeterminowanymi,
zaś fazy są niezależnymi zmiennymi losowowymi o
rozkładach równomiernych w przedziale od 0 do 2
π
. Taki
najmniej korzystny rozkład fazy został przyjęty także w
punkcie 2.3, gdzie liczony był stosunek wiarygodności dla
pojedynczego impulsu. Łączna funkcja gęstości
prawdopodobieństwa fazy będzie równa
)...
(
)
(
,...)
,
(
1
0
1
0
β
β
β
β
p
p
p
=
(3.6)
gdzie
)
π
β
π
β
β
2
;
0
2
1
...
)
(
)
(
1
0
∈
=
=
=
dla
p
p
W celu obliczenia stosunku wiarygodności wykorzystane
zostaną ogólne wyrażenie na stosunek wiarygodności
sygnału o nieznanych parametrach (2.4), oraz zależności z
punktu 2.3.
Wykorzystując, podobnie jak w punkcie 2.3 wzór na
cosinus sumy wyrażenie (3.5) można sprowadzić do
postaci:

62
∑
+
=
i
i
i
i
i
n
x
n
x
n
x
]
sin
)
(
cos
)
(
[
,...)
,
,
(
2
1
1
0
β
β
β
β
w której to:
)]
(
sin[
)
(
)
(
)]
(
cos[
)
(
)
(
2
1
n
n
n
X
n
x
n
n
n
X
n
x
i
i
i
i
i
i
ϕ
θ
ϕ
θ
+
−
=
+
=
Statystyka G
N
może być zapisana jako
∑
∑
+
=
=
−
=
i
i
i
i
i
N
k
N
z
z
k
y
k
x
G
]
sin
cos
[
)
(
,...)
,
,
(
,...)
,
(
2
1
1
0
1
0
1
0
β
β
β
β
β
β
przy czym
∑
∑
−
=
−
=
=
=
1
0
2
2
1
0
1
1
)
(
)
(
)
(
)
(
N
k
i
i
N
k
i
i
k
y
k
x
z
k
y
k
x
z
Wprowadzając, analogicznie jak w punkcie 2.3 poniższe
oznaczenia
2
2
2
1
i
i
i
z
z
Z
+
=
(3.7)
i
i
i
i
i
i
Z
z
Z
z
2
1
sin
cos
=
=
α
α
statystykę G
N
można przedstawić poniższym wyrażeniem:
∑
−
=
i
i
i
i
N
Z
G
)]
cos(
[
,...)
,
(
1
0
α
β
β
β
(3.8)
Jeśli przyjąć, że rozpatrywana paczka składa się z
impulsów nie pokrywających się wzajemnie w czasie, to
energię całej paczki można obliczyć sumując energię
poszczególnych impulsów. Biorąc pod uwagę to, że
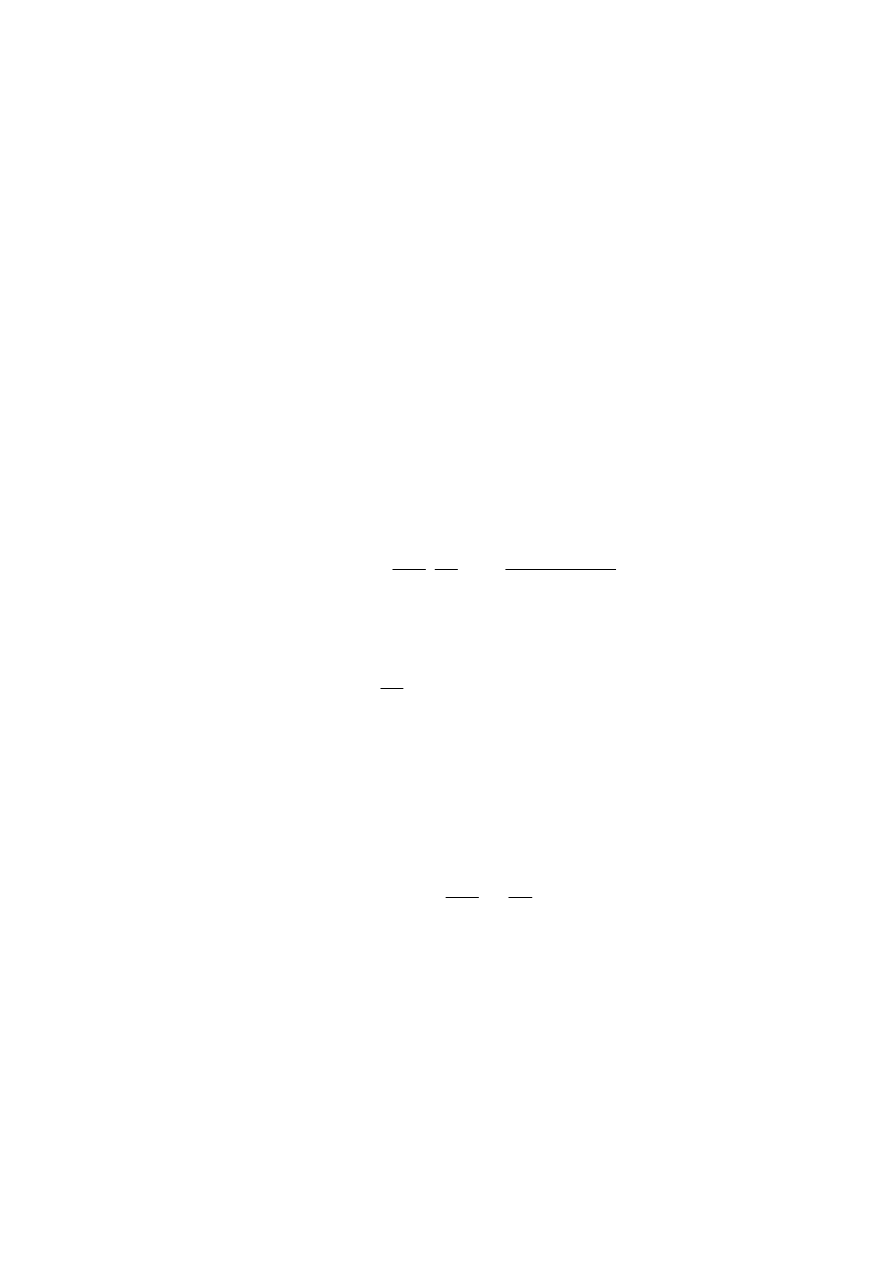
63
energia dla pojedynczego impulsu (punkt 2.3) nie jest
zależna od fazy można zapisać, że:
∑
∑
=
=
i
i
i
i
i
x
E
E
E
)
(
,...)
,
(
1
0
β
β
β
(3.9)
gdzie E
i
jest energią
i
-tego impulsu. Teraz korzystając ze
wzoru (2.4) na stosunek wiarygodności dla sygnału o
nieznanych parametrach można określić wartość tego
ilorazu dla paczki impulsów o nieznanych fazach.
Można go zapisać w postaci poniższego iloczynu:
∏
∫
−
−
=
i
i
i
i
i
i
d
Z
E
l
π
β
σ
α
β
π
σ
2
0
2
2
]
)
cos(
exp[
2
1
)
2
exp(
(3.10)
Wiedząc, że
)
(
2
1
0
2
0
)
cos(
u
I
d
e
u
∫
=
−
π
α
β
β
π
jest zmodyfikowaną funkcją Bessela pierwszego rodzaju
zerowego rzędu otrzymuje się ostateczne wyrażenie na
stosunek wiarygodności:
∏
−
=
i
i
i
Z
I
E
l
)
(
)
2
exp(
2
0
2
σ
σ
(3.11)
Porównując wyrażenie (3.11) z wyrażeniem (2.9) z punktu
2.3 widać, że stosunek wiarygodności dla sygnału w
postaci paczki impulsów nie pokrywających się
wzajemnie w czasie z przypadkowymi i niezależnymi

64
fazami jest iloczynem stosunków wiarygodności
obliczonych dla każdego impulsu z paczki.
3.3. DETEKTOR DLA SYGNAŁU W POSTACI PACZKI
IMPULSÓW W.CZ. O NIEZNANYCH FAZACH
W punkcie tym zostanie przeanalizowany integrator odbierający
sygnał w postaci paczki impulsów wielkiej częstotliwości o
przypadkowych (i niezależnych) fazach początkowych, a następnie
sumujący
I
impulsów i porównujący sumę z pewnym progiem
0
l
.
Punktem wyjścia dla rozważań będzie wyprowadzone w poprzednim
punkcie 3.2 wyrażenie (3.11) na stosunek wiarygodności:
∏
−
=
i
i
i
Z
I
E
l
)
(
)
2
exp(
2
0
2
σ
σ
Po zlogarytmowaniu powyższego wyrażenia otrzyma się, że:
∑
∑
−
=
i
i
i
i
E
Z
I
l
2
2
0
2
)
(
ln
ln
σ
σ
(3.12)
Operacje mnożenia zostały sprowadzone do operacji dodawania.
Ponieważ funkcja logarytmiczna jest ściśle monotoniczna, to
zamiast liczyć stosunek wiarygodności
l
i porównywać go z progiem
0
l
można określić wartość
l
ln
i porównać ją z odpowiednim progiem
0
ln l
. Jeśli
0
ln
ln
l
l
>
, znaczy że prawdziwa jest hipoteza H
1
i wykryto
obiekt. W przeciwnym przypadku prawdziwa jest hipoteza H
0
.
Podejście takie pozwala na znaczne uproszczenie budowy
detektorów. Detektor taki powinien wykonać operacje matematyczne
opisane poniższym wyrażeniem:

65
∑
i
i
Z
I
)
(
ln
2
0
σ
Pierwszym etapem jest znalezienie wartości statystyki Z
i
dla
każdego
i
-tego impulsu. Zgodnie z rozważaniami z punktu 2.5 jeśli
sygnał y(n) jest obserwowany w zakresie n od 0 do N
1
-1, to można
ją zapisać wyrażeniem (2.30):
∑
−
=
≅
1
0
1
)
(
*
)
(
2
1
N
k
i
i
k
k
Z
X
Y
,
gdzie X
i
(n) i Y(n) są zespolonymi amplitudami przebiegów x
i
(n)
oraz
y(n). W powyższym wyrażeniu
)]
(
exp[
)
(
)
(
n
j
n
X
n
xi
i
ϕ
=
i
X
jest znaną funkcją zależną od położenia na osi czasu. Aby
zniwelować modulację amplitudy paczki przez charakterystykę
anteny radaru zostaną wprowadzone współczynniki wagowe S
i
. Dla
największego impulsu z paczki zostanie przyjęte S
max
=1. Ponadto
oznaczając przez n
i
moment wysłania
i
-tego impulsu sondującego,
a przez n
opi
czas jego opóźnienia (związany z odległością obiektu od
stacji radarowej) można zapisać funkcję X
i
(n) w postaci:
)
)
(
exp(
)
(
)
(
θ
opi
i
opi
i
i
n
n
j
n
n
n
S
n
+
−
⋅
−
−
⋅
=
U
X
i
(3.13)
Wtedy
i
i
i
Z
S
Z
0
=
,
gdzie dla każdego impulsu
∑
−
=
−
−
≅
1
0
0
1
)
(
*
)
(
2
1
N
k
opi
i
i
n
n
k
k
Z
U
Y
(3.14)
Porównując wyrażenie (3.14) z wyrażeniem (2.34) z punktu 2.5
widać, że wszystkie wielkości Z
0i
można otrzymać za pomocą
detektora przedstawionego na rysunku 2.5. Składa się on z filtru
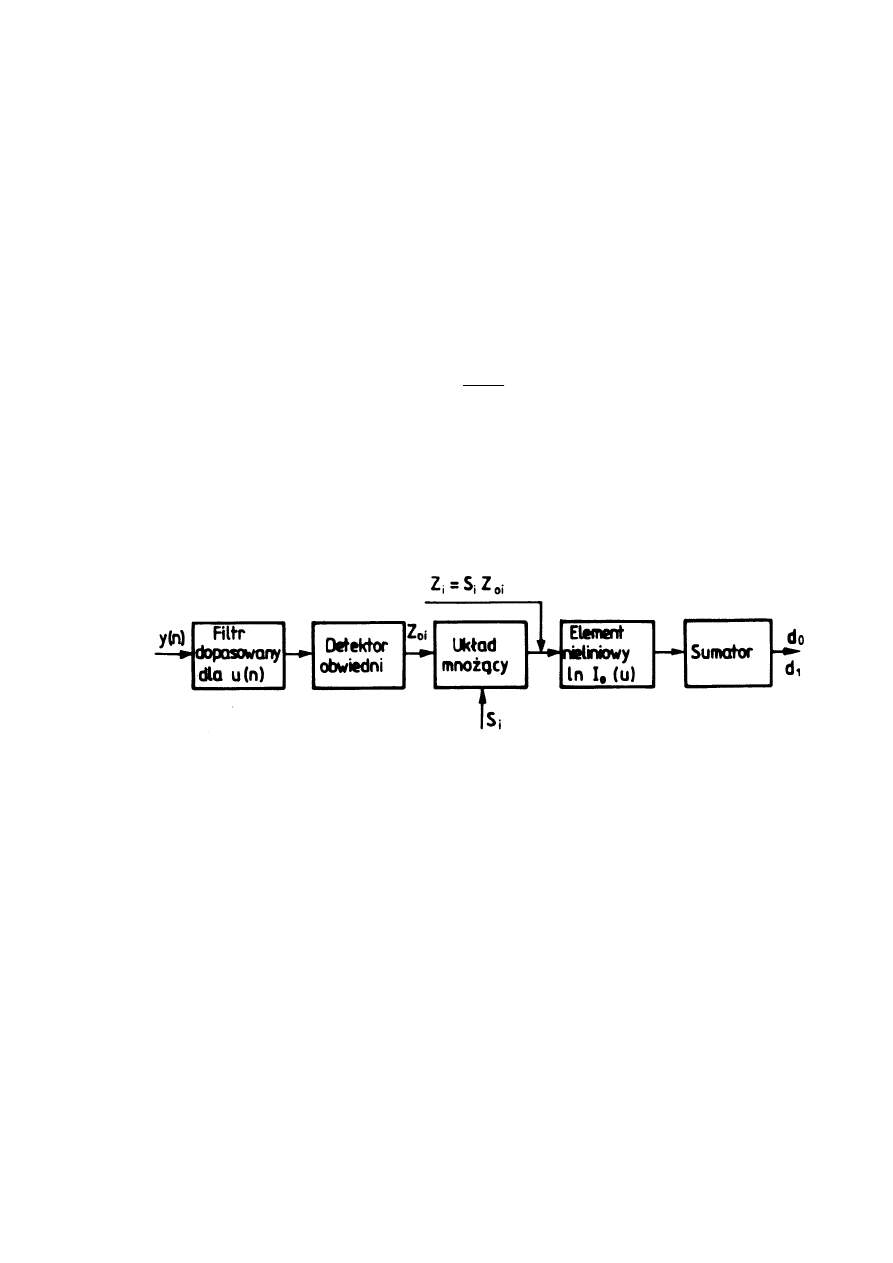
66
dopasowanego do impulsu u(n) oraz detektora obwiedni. Aby
otrzymać wielkość Z
i
należy go poszerzyć o układ wprowadzający
współczynniki wagowe S
i
. Tak więc w wyniku pierwszego etapu
obróbki paczki niekoherentnej impulsów wielkiej częstotliwości
otrzyma się paczkę obwiedni impulsów branych z odpowiednią
wagą.
Kolejny etap obróbki polega na obliczeniu wartości
)
(
ln
2
0
0
σ
i
i
Z
S
I
dla każdego
i
oraz ich zsumowaniu. Wynik sumowania nie zależy
od początkowych faz impulsów w.cz. gdyż dodaje się ich obwiednie.
Całkowity układ obróbki jest przedstawiony na poniższym rysunku
3.5.
Rys. 3.5. Schemat blokowy układu optymalnej detekcji paczki impulsów wielkiej częstotliwości o
nieznanych fazach
Składa się on z filtru dopasowanego do impulsu u(n), detektora
obwiedni, układu mnożącego przez współczynniki obwiedni paczki
S
i
, bloku nieliniowego o charakterystyce
)
(
ln
0
u
I
oraz sumatora, który
skupia w czasie niejednoczesne obwiednie impulsów, a następnie
dodaje je do siebie.
W sytuacjach krańcowych, gdy poziomy sygnałów (impulsów)
są albo bardzo słabe, albo bardzo silne można schemat z rysunku
3.5 znacznie uprościć. Jak wiadomo z właściwości funkcji Bessela,
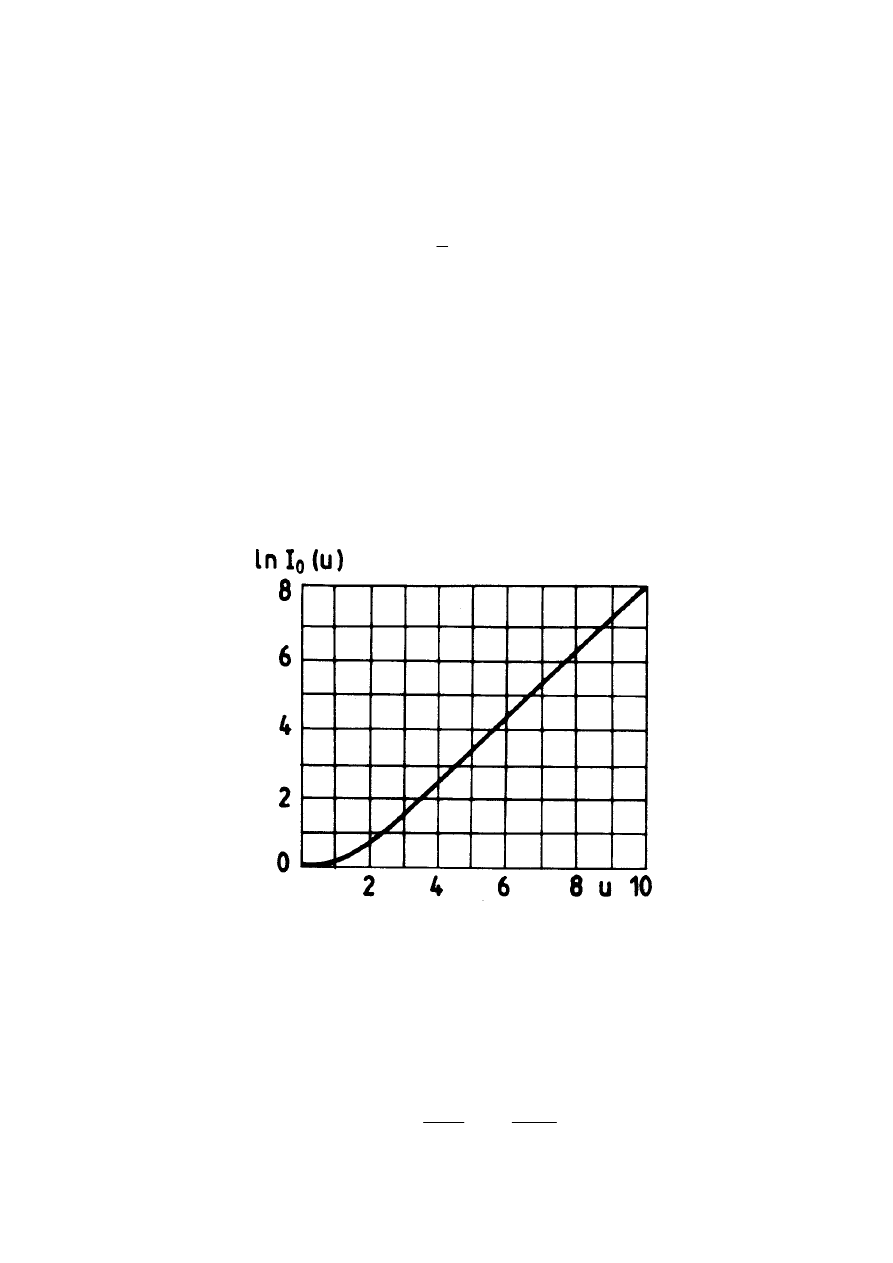
67
dobrą aproksymacją funkcji
)
(
ln
0
u
I
dla małych wartości argumentu
u=S
i
Z
0i
/
σ
2
jest pierwszy człon szeregu potęgowego, na który można
ją rozłożyć [5]:
1
,
4
1
)
(
ln
2
0
<<
≅
u
dla
u
u
I
(3.15)
Oznacza to, że początkowa część jej przebiegu ma charakter
paraboliczny. Natomiast dla dużych wartości argumentu u funkcję
można zastąpić przebiegiem asymptotycznym:
1
,
)
(
ln
0
>>
≅
u
dla
u
u
I
(3.16)
co wskazuje na liniowy kształt jej wykresu na tym odcinku. Wykres
funkcji
)
(
ln
0
u
I
jest pokazany na poniższym wykresie 3.6.
Rys. 3.6. Wykres funkcji
)
(
ln
0
u
I
W związku z tym dla paczki impulsów o amplitudach małych w
porównaniu z szumami wychodzi, że:
∑
∑
≅
i
i
i
i
i
i
Z
S
Z
S
I
4
2
0
2
2
0
0
4
)
(
ln
σ
σ
(3.17)

68
zaś dla impulsów o dużych amplitudach
∑
∑
≅
i
i
i
i
i
i
Z
S
Z
S
I
2
0
2
0
0
)
(
ln
σ
σ
.
(3.18)
W ten sposób dodawanie logarytmów zostało zastąpione przez
sumowanie liniowych lub kwadratowych funkcji wielkości Z
0i
. W
detektorze z rysunku 3.5 w przypadku dużych sygnałów w ogóle
zniknie blok nieliniowy o charakterystyce
)
(
ln
0
u
I
, zaś dla małych
sygnałów zostanie zastąpiony układem mnożącym, na którego oba
wejścia zostaną podane kolejne S
i
Z
0i
.
3.4. INTEGRATOR BINARNY
W poprzednim punkcie przedstawiono detektor, który kumuluje odebrane
impulsy echa radarowego w jednej wartości. W zależności od poziomu sygnału
sumował obwiednie impulsów lub ich kwadraty i porównywał z wartością
progową. Jednak przedstawione w punkcie 3.3 rozwiązanie ma pewną wadę.
Jest wrażliwe na sygnały o bardzo dużej amplitudzie, nie będące rzeczywistym
echem. Mogą to być np. aktywne zakłócenia impulsowe wygenerowane celowo
przez wrogi obiekt, aby uniemożliwić pracę radaru [2]. Przykładowo integrator
kumulujący
5
=
I
impulsów w momencie, gdy cztery odebrane będą tylko
szumem, a piąty odpowiednio wysokim impulsem zakłócającym wywoła
fałszywy alarm. Wrażliwość na zbyt duże impulsy nie jest tylko cechą
integratora z punktu 3.3, ale wszystkich, w których kumulant, na podstawie
którego podejmuje się decyzję tworzony jest bezpośrednio z amplitudy sygnału.
Aby pozbyć się wspomnianego problemu można zastosować tzw.
integrator dwuprogowy. Zwany jest często integratorem binarnym lub
detektorem M-z-N, gdzie N oznacza ilość integrowanych impulsów w paczce.
Integrator ten ma wiele zalet. Po za tym, że nie jest wrażliwy na duże skoki
amplitudy pojedynczych impulsów, łatwo go zaimplementować oraz działa
bardzo dobrze gdy rozkład zakłóceń jest różny od rozkładu Rayleya [2, 11].
Jego schemat blokowy pokazany jest na poniższym rysunku 3.7.
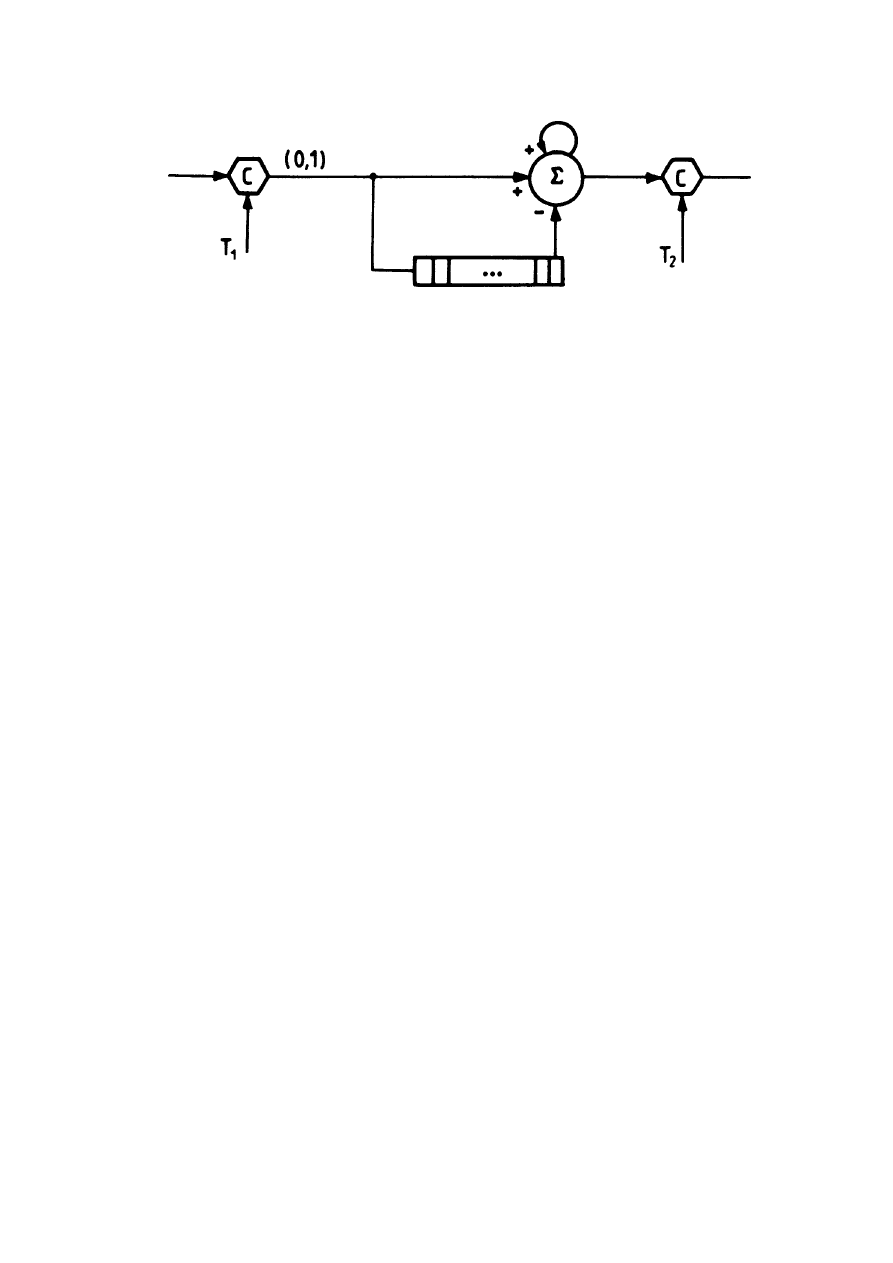
69
Rys. 3.7. Schemat blokowy integratora binarnego (dwuprogowego). ‘C’ oznacza porównywanie
z progami decyzyjnymi
Jak to jest pokazane na schemacie impulsy wejściowe są kwantowane do
wartości 1 lub 0, w zależności od tego, czy przekroczony lub nie zostanie próg
T
1
. Zakłada się przy tym prostokątną obwiednię paczki impulsów tzn. każdy
impuls został przemnożony przez odpowiedni współczynnik S
i
niwelujący wpływ
charakterystyki anteny na obwiednię paczki. Ostatnie N jedynek i zer jest
sumowane i porównywane z drugim progiem T
2
=M. Mówiąc inaczej sumowanie
liniowe lub kwadratowe występujące w detektorach operujących bezpośrednio
na amplitudzie sygnału zostało zastąpione zliczaniem impulsów, które
przekroczyły próg T
1
.
3.5. FAŁSZYWY ALARM
W analizie detektorów otoczenie stacji radarowej przyjmuje się zwykle
jako znane i homogeniczne (jednorodne). Przy takim założeniu można
stosować w detektorach stały poziom progu wykrywania. Jednakże w
rzeczywistym środowisku, znajdują się liczne pofałdowania terenu, morza,
padają deszcze i występują gęste chmury. Wszystkie te elementy środowiska
odbijają sygnały radiolokacyjne, pochodzące zarówno z własnej stacji
radarowej, jak i z obcych. Przestrzeń wokół radaru pełna jest biernych zakłóceń
(ang. clutter) i przy stosowaniu stałego progu detekcji może pojawić się
olbrzymia liczba fałszywych alarmów. Te z kolei mogą nadmiernie przeciążyć
cyfrowy system obróbki danych. Rysunek 3.8 na następnej stronie pokazuje
wzrost poziomu fałszywego alarmu spowodowany wzrostem poziomu zakłóceń.
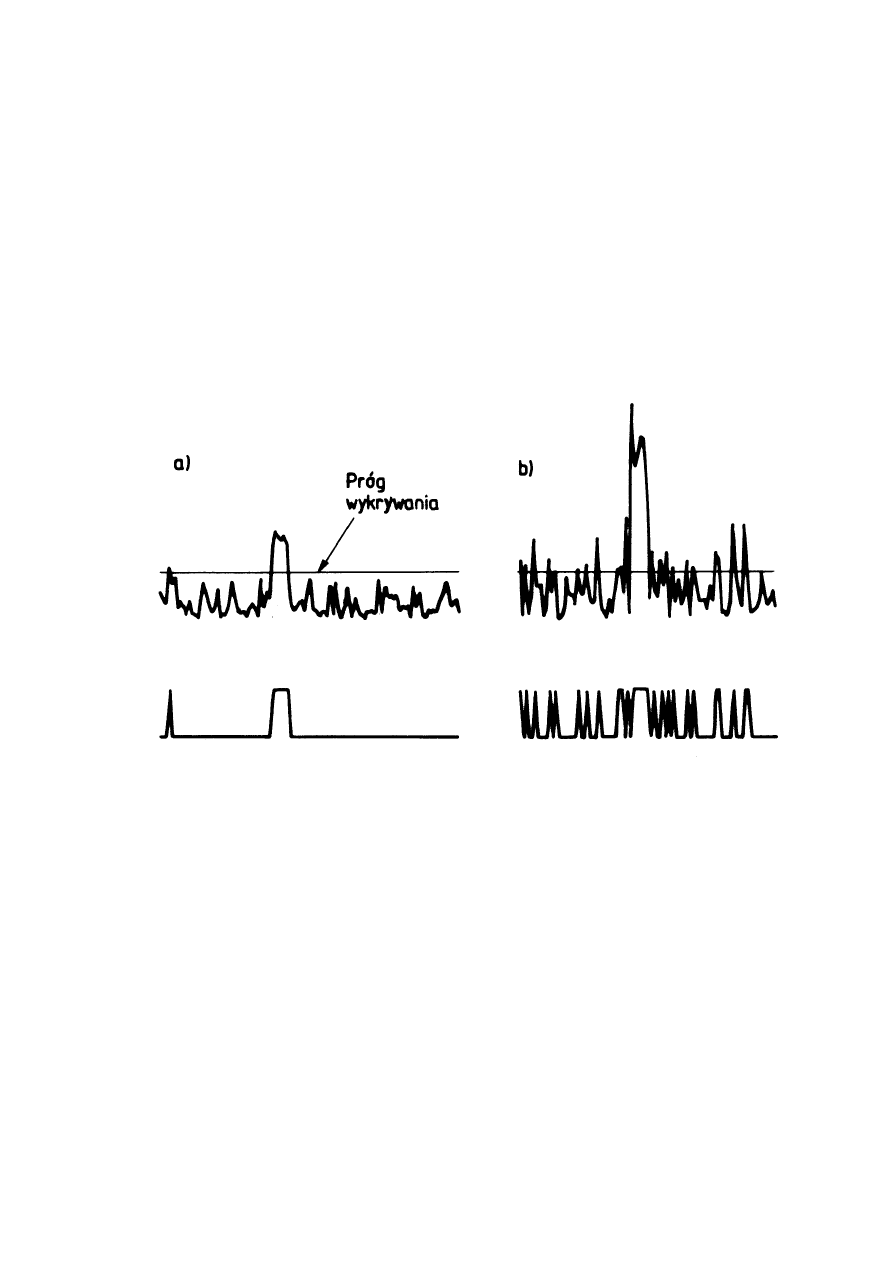
70
Jedną z metod ograniczenia fałszywych alarmów w systemach ze stałym
progiem jest jego podniesienie. Niestety takie rozwiązanie zmniejszy
wykrywalność obiektów znajdujących się w obszarze o niskim poziomie
zakłóceń biernych. Zamiast tego stosuje się inne metody stabilizacji poziomu
prawdopodobieństwa fałszywego alarmu (ang. Constant False Alarm Ratio
−
CFAR) polegające na stabilizacji poziomu zakłóceń lub na automatycznej
zmianie poziomu progu w zależności od poziomu zakłóceń albo, na kombinacji
obu tych metod.
Rys. 3.8. Wpływ wielkości zakłóceń na liczbę przekroczeń progu decyzyjnego i poziom
fałszywego alarmu: (a)
−
niski poziom zakłóceń, (b)
−
wysoki poziom zakłóceń
Obie metody opierają się na założeniu, że środowisko jest jednorodne na
małym obszarze wokół komórki odległościowej, która aktualnie jest testowana.
Próbki sygnału z komórek odległościowych otaczających komórkę testowaną
(zwane komórkami odniesienia) są statystycznie niezależne i mają takie same
rozkłady.
W przypadku układów CFAR z progiem automatycznie adaptującym się
do poziomu szumów przyjmuje się, że funkcja gęstości prawdopodobieństwa
szumu jest znana poza kilkoma parametrami. Komórki odniesienia otaczające
komórkę testową są wykorzystywane do estymacji tych nieznanych
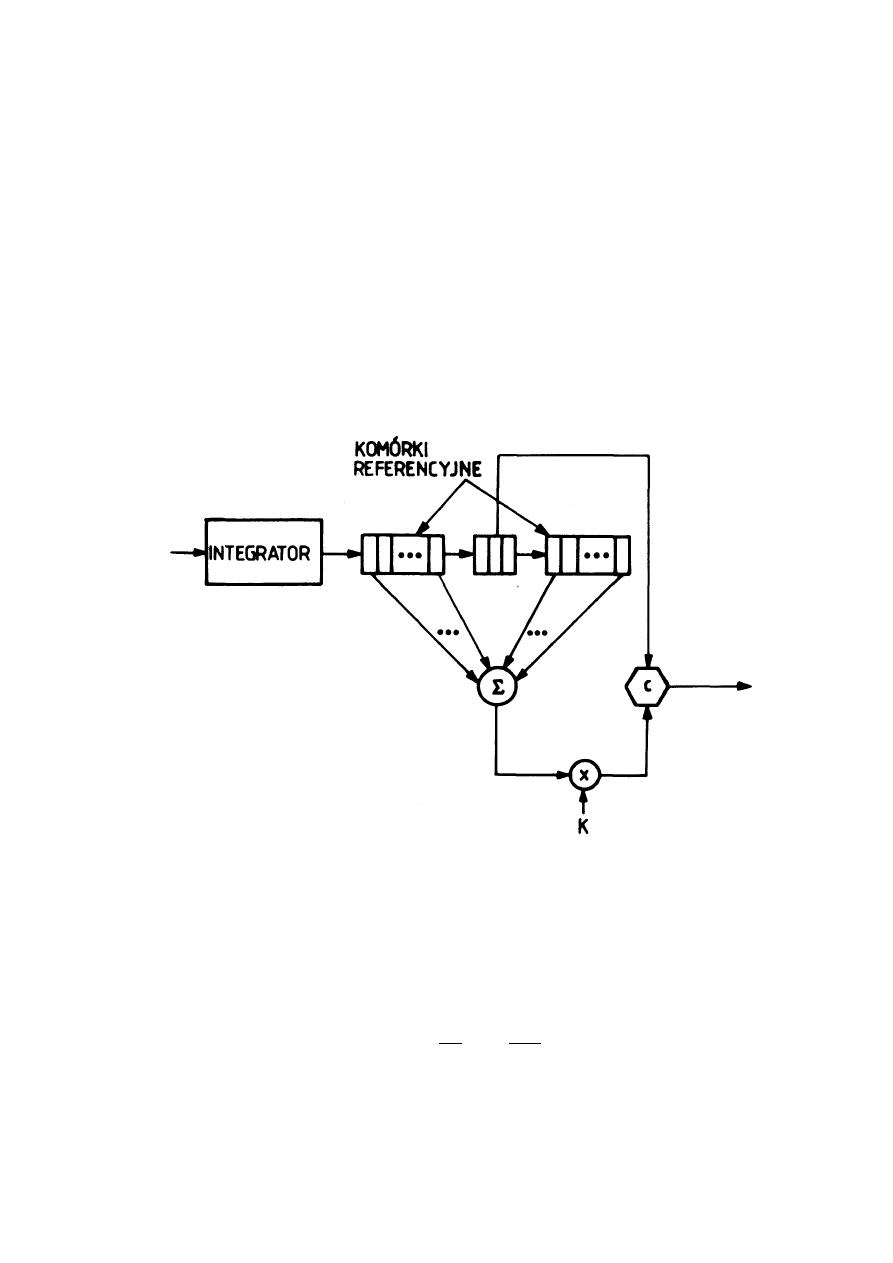
71
parametrów, a na podstawie ich estymat ustalany jest poziom progu detekcji.
Decyzję o obecności obiektu podejmuje się jeśli poziom sygnału z komórki
testowej jest dostatecznie duży w porównaniu z komórkami referencyjnymi
Najprostszy i najszerzej stosowany jest układ CFAR z rysunku 3.9 na
stronie dalej, bazujący na uśrednianiu odległościowym. Detektor ten był szeroko
badany przez Finna i Johnsona [11].
Rys. 3.9. Schemat blokowy układu CFAR z uśrednianiem odległościowym i progiem
automatycznie adaptującym się do poziomu szumów. ‘C’ oznacza porównywanie z progiem
decyzyjnym. Przed układem CFAR umieszczono integrator
Jeśli zakłócenia mają rozkład Rayleya tzn.
)
2
exp(
)
(
2
2
2
σ
σ
x
x
x
p
−
=
tylko jeden parametr
σ
musi być estymowany (
σ
2
jest mocą szumu). Próg
detekcji można określić z poniższego wyrażenia:
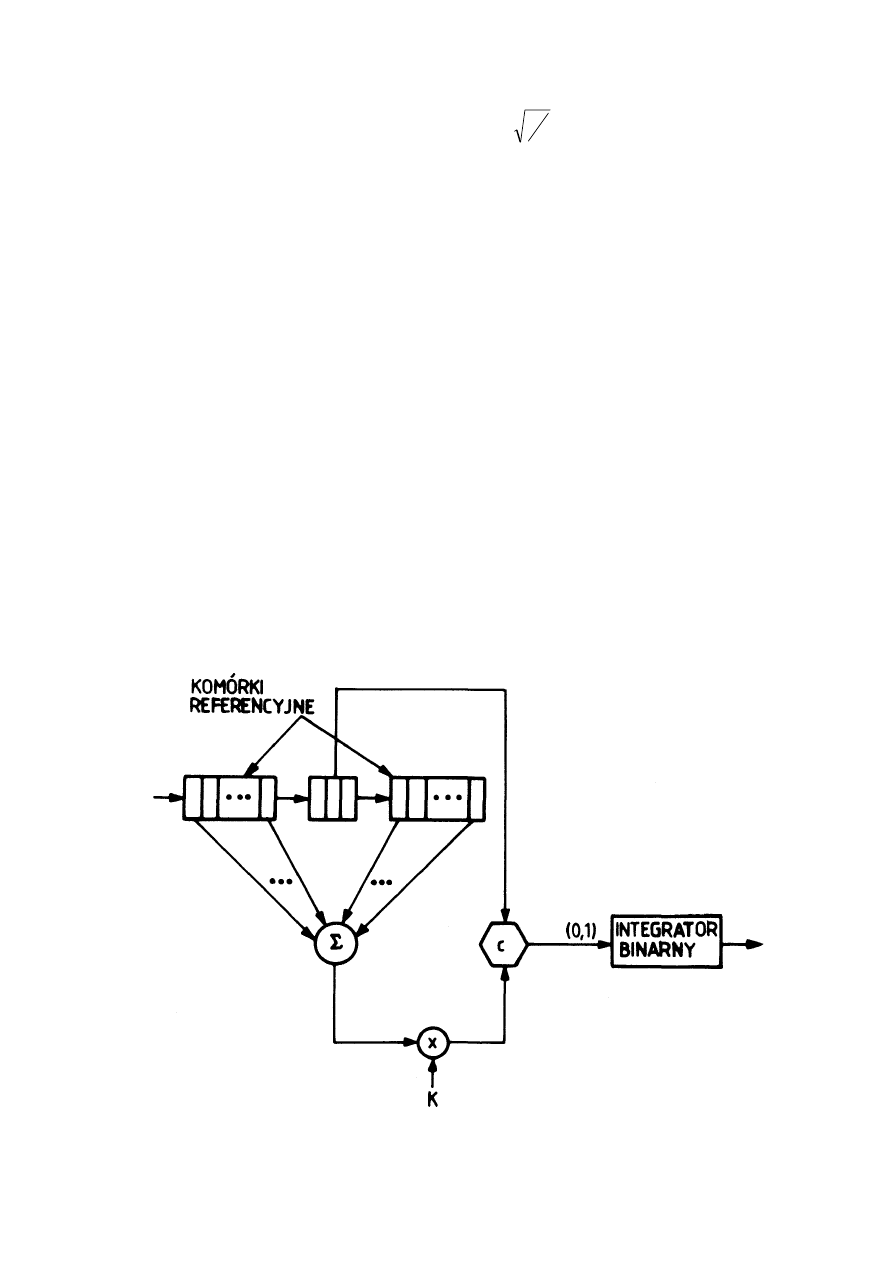
72
σ
π
ˆ
2
⋅
⋅
=
⋅
=
∑
nK
x
K
T
i
i
(3.19)
gdzie
σ
ˆ
jest estymatą parametru
σ
, zaś n ilością komórek odniesienia.
Ponieważ próg T jest ustalany przez estymatę
σ
ˆ
która jest określona z pewnym
błędem, trzeba go podnieść nieco wyżej „na wszelki wypadek”, niż gdyby był
dokładnie znany a priori. Dodatkowy zapas poziomu progu powoduje
pogorszenie czułości detektora i jest traktowany jako straty wprowadzone przez
CFAR. Jakość estymacji parametru
σ
zależy od tego, na bazie ilu komórek
referencyjnych obliczona zostanie estymata
σ
ˆ
. Dla małej ich ilości strata CFAR
jest duża z powodu kiepskiej jakości estymacji. Z kolei zbyt duża ich liczba
może spowodować naruszenie założenia o jednorodności obszaru tylko w
małym otoczeniu komórki testowej. Dobrą praktyczną zasadą jest użycie takiej
liczby komórek odniesienia, aby utrzymać straty CFAR poniżej 1dB [11]. W
przypadku wątpliwości, czy zakłócenia faktycznie mają rozkład Rayleya należy
zmodyfikować układ z rys. 3.9 usuwając integrator sprzed bloku CFAR. Lepiej
jest uśredniać odległościowo i porównywać z progiem pojedyncze impulsy oraz
zastosować opisany w punkcie 3.4 integrator binarny (dwuprogowy). Schemat
układu pokazany jest na rysunku 3.10.
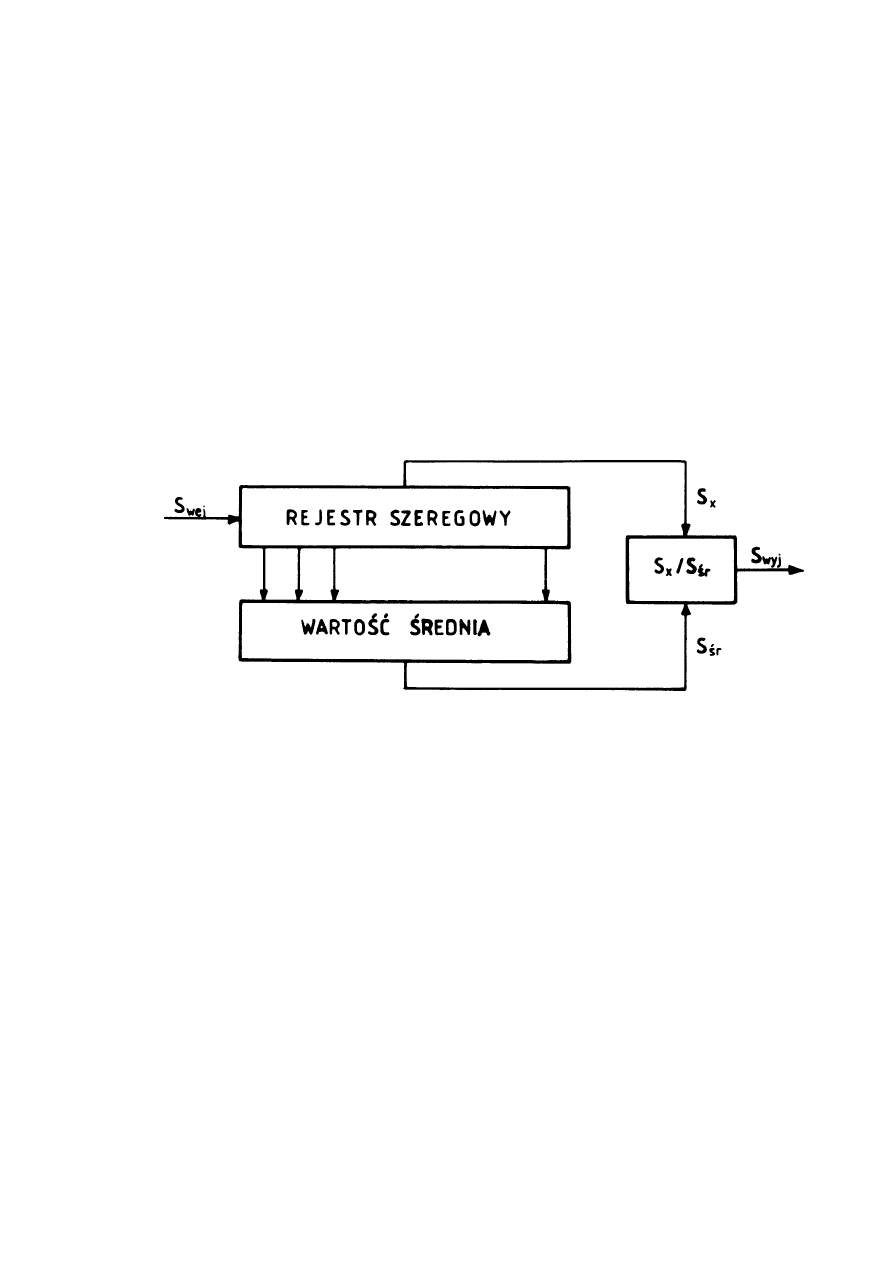
73
Rys. 3.10. Schemat blokowy układu CFAR z uśrednianiem odległościowym i progiem
automatycznie adaptującym się do poziomu szumów wraz z integratorem binarnym. ‘C’
oznacza porównywanie z progiem decyzyjnym
Zastosowanie takiego rozwiązania z integratorem binarnym jest także
przydatne, gdy moc zakłóceń zmienia się z każdym impulsem.
Układy CFAR, których działanie polega na stabilizacji poziomu zakłóceń
także bazują na uśrednianiu odległościowym impulsów. Jednak w
przeciwieństwie do układów opisanych wyżej tu poziom progu jest cały czas
stały. Przykład takiego układu jest pokazany na kolejnej stronie na rysunku
3.11.
Rys. 3.11. Schemat blokowy układu CFAR z uśrednianiem odległościowym i stałym progiem
Tak jak w układach z rysunków 3.9 i 3.10 próbki sygnału radiolokacyjnego
wprowadzane są do rejestru przesuwnego. Następnie liczona jest wartość
średnia z próbek pochodzących z komórek odległościowych otaczających
obustronnie komórkę testową. W wyniku podzielenia wartości sygnału S
x
z
komórki testowej przez wartość średnią S
sr
otrzymuje się w sygnale wyjściowym
S
wyj
stabilizowany poziom szumu. Przez pojęcie „stabilizowany” należy
rozumieć, że zmienia się on w stopniu mniejszym niż poziom szumu
wejściowego. Analogicznie, jak w poprzednim układzie stopień stabilizacji
szumu zależy od tego, na bazie ilu komórek odległościowych otaczających
komórkę testową liczy się wartość średnią.
Przedstawione na rysunkach 3.9
−
3.11 schematy blokowe układów CFAR
są najbardziej podstawowymi ich realizacjami. W praktyce układy te są w różny

74
sposób modyfikowane. Jedną z możliwych zmian jest wstawienie na wejściu
bloku przetwornika liniowo-logarytmicznego. Dzięki temu zapewnia się
poprawną pracę układu w szerokim zakresie wartości sygnału wejściowego i
zastępuje się operację dzielenia próbek prostszą operacją odejmowania [2].
We współczesnych radarach klasyczne układy CFAR stabilizujące poziom
szumów są wspomagane przez układy bazujące na zasadzie uśredniania
powierzchniowego. Znane są one pod nazwą map zakłóceń biernych (ang.
clutter map). Obszar wokół stacji radarowej dzieli się na komórki azymutalno-
odległościowe i dla każdej zapamiętuje poziom zakłóceń. Zakładając, że w
długim okresie czasu rozkład przestrzenny zakłóceń nie ulega zmianie, można
obliczyć średni poziom zakłóceń za okres pewnej liczby sondowań
otaczającego obszaru. Uzyskane tak wartości można wykorzystać do
ustawienia poziomu progu decyzyjnego. W ten sposób próg nie ma stałego
poziomu dla całego obszaru obserwowanego przez radar, ale jest dostosowany
do poziomu zakłóceń w każdej komórce rozróżnialności.
4. ANALIZA JAKOŚCI UKŁADÓW OPTYMALNEJ
DETEKCJI SYGNAŁÓW RADIOLOKACYJNYCH
Najlepszą w sensie statystycznym jakość wykrywania i estymacji
parametrów sygnałów radiolokacyjnych można uzyskać tylko poprzez ich
optymalną obróbkę. Jak wspomniano w rozdziale pierwszym, jakość detekcji
określa się poprzez prawdopodobieństwo poprawnego wykrycia D przy
ustalonym prawdopodobieństwie fałszywego alarmu F. Prawdopodobieństwo
detekcji określa się dla różnych stosunków energii sygnału użytecznego do
mocy zakłóceń. Zgodnie z kryterium Neymana-Pearsona dla stałego poziomu F
dąży się do maksymalizacji D. Obliczanie jakości układów optymalnych ma
znaczenie, ponieważ jakość ta ukazuje granicę, do której dąży się przybliżając
układ rzeczywisty do optymalnego. W poprzednich rozdziałach opisana została
budowa i sposób działania układów detekcji, które realizują obróbkę sygnałów
zbliżoną do optymalnej. W tym rozdziale zostaną przeanalizowane
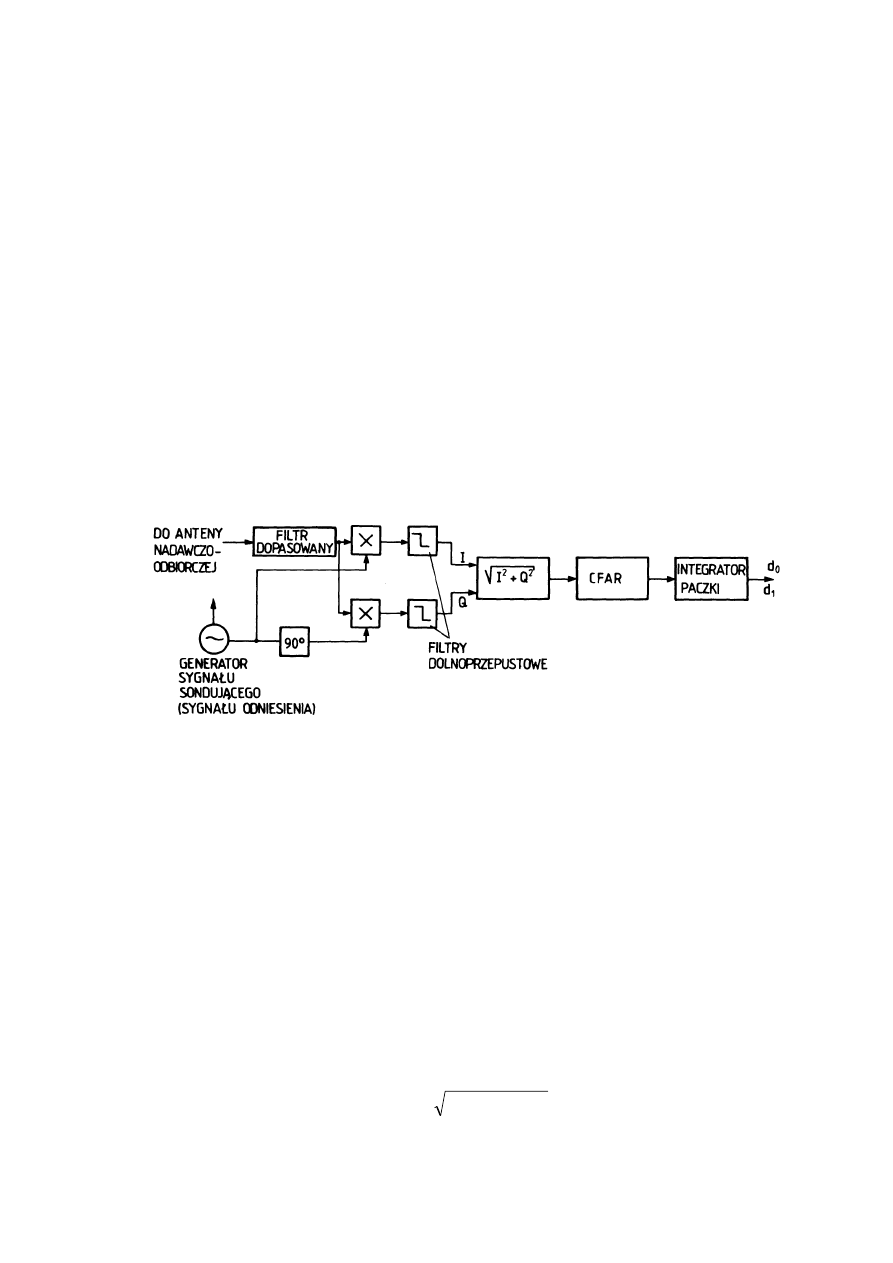
75
poszczególne bloki systemu, wykonujące różne operacje na sygnale echa
radarowego zakłóconego szumem. Pokazane zostaną metody pozwalające
wyliczyć rozkłady prawdopodobieństw przebiegów na ich wyjściu w przypadku
odbierania jedynie zakłóceń oraz dla sygnału użytecznego wraz z addytywnymi
zakłóceniami. Ich zastosowanie wymaga wielu obliczeń, które w postaci
analitycznej są żmudne i skomplikowane. Metody te można jednak z
powodzeniem zastosować do obliczeń numerycznych. W oparciu o nie został
stworzony zbiór funkcji pracujących w środowisku MATLAB. Za ich pomocą
wyliczono przedstawione dalej rozkłady prawdopodobieństw i wykreślone na ich
podstawie charakterystyki detekcji dla bloków systemu radarowego. Schemat
systemu przetwarzania sygnału w radarach z podziałem na bloki funkcjonalne
pokazano na następnej stronie na rysunku 4.1.
Rys. 4.1. Schemat blokowy sytemu przetwarzania danych w systemach radarowych
4.1. ROZKŁADY OBWIEDNI SYGNAŁU
W najprostszym przypadku w systemie nie występuje blok stabilizacji
poziomu fałszywego alarmu (CFAR) oraz integrator paczki impulsów. Decyzję o
obecności sygnału w szumie podejmuje się porównując amplitudę chwilową
(obwiednię) sygnału za detektorem fazy z odpowiednio dobranym progiem.
Zgodnie z powyższym schematem obwiednia równa jest pierwiastkowi
kwadratowemu z sumy kwadratów składowych I i Q :
)
(
)
(
)
(
2
2
n
Q
n
I
n
Z
+
=
(4.1)
Składowe te można zapisać jak poniżej:
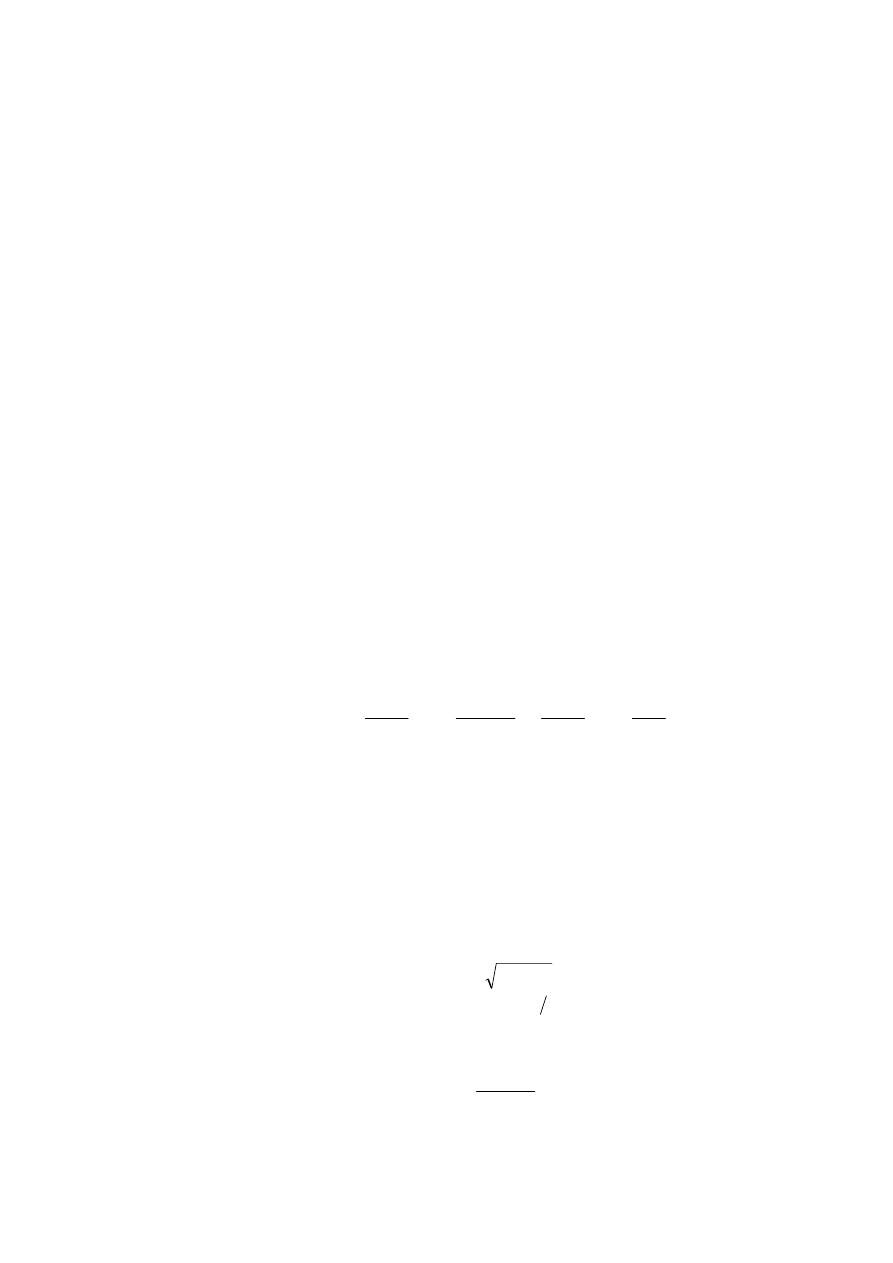
76
))
(
sin(
)
(
)
(
))
(
cos(
)
(
)
(
n
n
n
Y
n
Q
n
n
n
Y
n
I
y
d
y
d
ϕ
θ
ϕ
θ
+
=
+
=
(4.2)
gdzie
θ
d
jest pulsacją dopplerowską (czyli różnicą pulsacji wzorcowej nadajnika
i pulsacji sygnału echa) określającą prędkość radialną obiektu, od którego
pochodzi echo. Przyglądając się postaci składowych I (n) oraz Q (n) widać, że
można je potraktować jako składowe (odpowiednio rzeczywistą i urojoną)
pewnego sygnału analitycznego. Skoro tak, to (wiadomo to z własności sygnału
analitycznego) zmienne losowe I (n) i Q (n) są dla danego n nieskorelowane,
oraz ich rozkłady prawdopodobieństwa są identyczne. Jednakowe są także
widmo mocy i wariancja obu przebiegów [6, 13].
W przypadku gdy prawdziwa jest hipoteza H
0
, to do odbiornika docierają
jedynie zakłócenia o zerowej wartości średniej. Pierszym etapem obliczeń jest
znalezienie łącznego rozkładu zmiennych losowych obu składowych I (n) i
Q (n) tzn.
).
,
( Q
I
p
Jeśli zmienne losowe I i Q są niezależne, to ich łączny
rozkład równy jest iloczynowi rozkładów obu zmiennych losowych:
)
(
)
(
)
,
(
,
Q
p
I
p
Q
I
p
Q
I
Q
I
=
(4.3)
Przykładowo gdy zakłócenia mają rozkład normalny, to łączny rozkład można
zapisać jak poniżej:
)
2
exp(
2
1
)
2
exp(
2
1
)
,
(
2
2
2
2
2
2
2
,
w
w
w
w
Q
I
Z
Q
I
Q
I
p
σ
πσ
σ
πσ
−
=
+
−
=
(4.4)
gdzie
σ
w
2
jest wariancją szumu za filtrem dopasowanym. Niech zmienna losowa
Z i dodatkowa zmienna
ϕ
będą wynikiem działania pewnego przekształcenia na
zmiennych losowych I i Q :
=
Q
I
g
Z
ϕ
(4.5)
gdzie funkcja g:R
2
→
R
2
określona jest poniższym wzorem (4.6):
+
=
)
(
1
2
2
2
2
1
2
1
x
x
arctan
x
x
x
x
g
(4.6)
Przekształcenie odwrotne g
-1
i jej pochodna mają postać:
−
=
=
−
)
cos(
)
sin(
)
sin(
)
cos(
)
(
,
)
sin(
)
cos(
2
1
2
2
1
2
1
2
1
2
1
2
1
y
y
y
y
y
y
dy
y
dg
y
y
y
y
y
y
g
(4.7)
natomiast modół jakobianu przekształcenia g
-1
równy jest
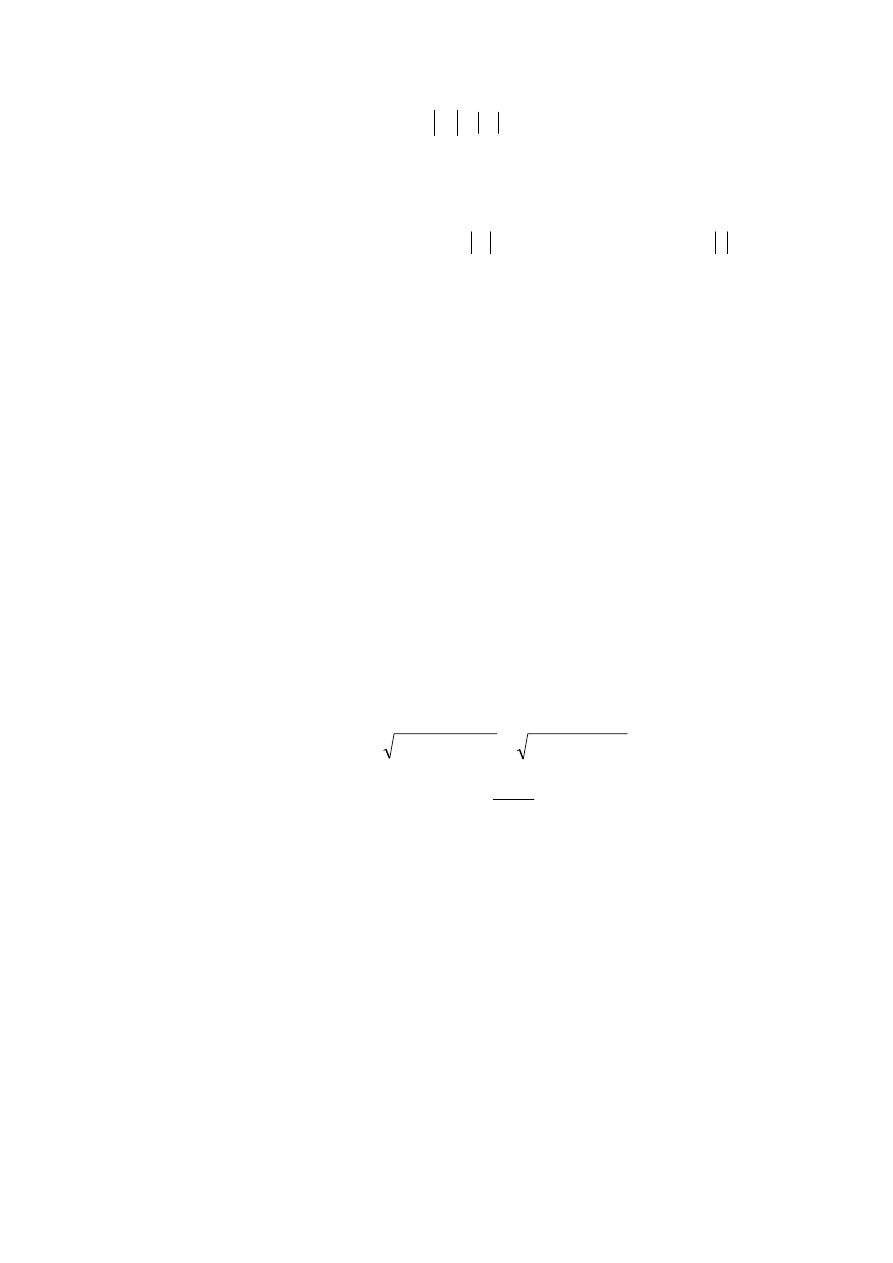
77
1
y
J
g
=
(4.8)
Znając go można określić łączny rozkład gęstości prawdopodobieństwa
zmiennych Z oraz
ϕ
wyrażony za pomocą zmiennych wejściowych I i Q :
I
Q
I
p
Q
I
p
y
y
y
y
y
p
y
y
p
Q
I
Q
I
Z
⋅
⋅
=
⋅
=
))
sin(
(
))
cos(
(
)
sin(
),
cos(
(
)
,
(
1
2
1
2
1
,
2
1
,
ϕ
(4.9)
Rozkład brzegowy zmiennej losowej Z uzyska się całkując rozkład p
Z,
ϕ
(y
1
, y
2
)
względem zmiennej y
2
:
∫
=
2
2
1
,
1
)
,
(
)
(
dy
y
y
p
y
p
Z
Z
ϕ
(4.10)
W przypadku, gdy prawdziwa jest hipoteza H
1
, to odbierany sygnał jest
sumą szumu o zerowej średniej (takiego jak w przypadku prawdziwości
hipotezy H
0
) i sygnału użytecznego. Niestety nie można postąpić identycznie,
jak dla hipotezy H
0
, zmieniając jedynie wartość średnią obu zmiennych I i Q
na równą energii lub amplitudzie sygnału użytecznego w zależności od tego,
czy w systemie jest filtr dopasowany, czy nie. Aby wyznaczyć rozkład obwiedni
p(Z), należy potraktować zakłócenia jako szum wąskopasmowy o
częstotoliwości centralnej
θ
d
. Można go wtedy zapisać poniższym wyrażeniem:
)
sin(
)
(
)
cos(
)
(
))
(
cos(
)
(
d
s
d
c
n
d
w
n
n
n
n
n
n
n
n
n
N
θ
θ
ϕ
θ
−
=
+
(4.11)
gdzie
)
(
)
(
)
(
)
(
)
(
)
(
2
2
2
2
n
n
n
n
n
Q
n
I
n
Z
n
N
s
c
w
+
=
+
=
=
(4.12)
)
)
(
)
(
(
tg
)
(
n
n
n
n
ac
n
c
s
n
=
ϕ
Jeśli przyjąć początek obserwacji przebiegu wejściowego tak, aby faza sygnału
użytecznego była zerowa, to suma zakłócenia i sygnału zgodnie z wyrażeniami
(4.11) i (4.12) równa jest
)
sin(
)
(
)
cos(
)
(
)
cos(
))
(
cos(
)
(
d
s
d
c
d
w
d
n
n
n
n
n
n
n
A
n
n
n
W
θ
θ
θ
ϕ
θ
−
+
=
+
(4.13)
gdzie A jest energią lub amplitudą sygnału użytecznego. Porównując stronami
to wyrażenie wychodzi, że
)
(
))
(
sin(
)
(
)
(
)
(
))
(
cos(
)
(
)
(
1
1
n
n
n
n
W
n
n
A
n
n
A
n
n
W
n
n
s
w
s
c
w
c
=
=
−
=
−
=
ϕ
ϕ
(4.14)
czyli obwiednia sumy zakłócenia i sygnału będzie równa
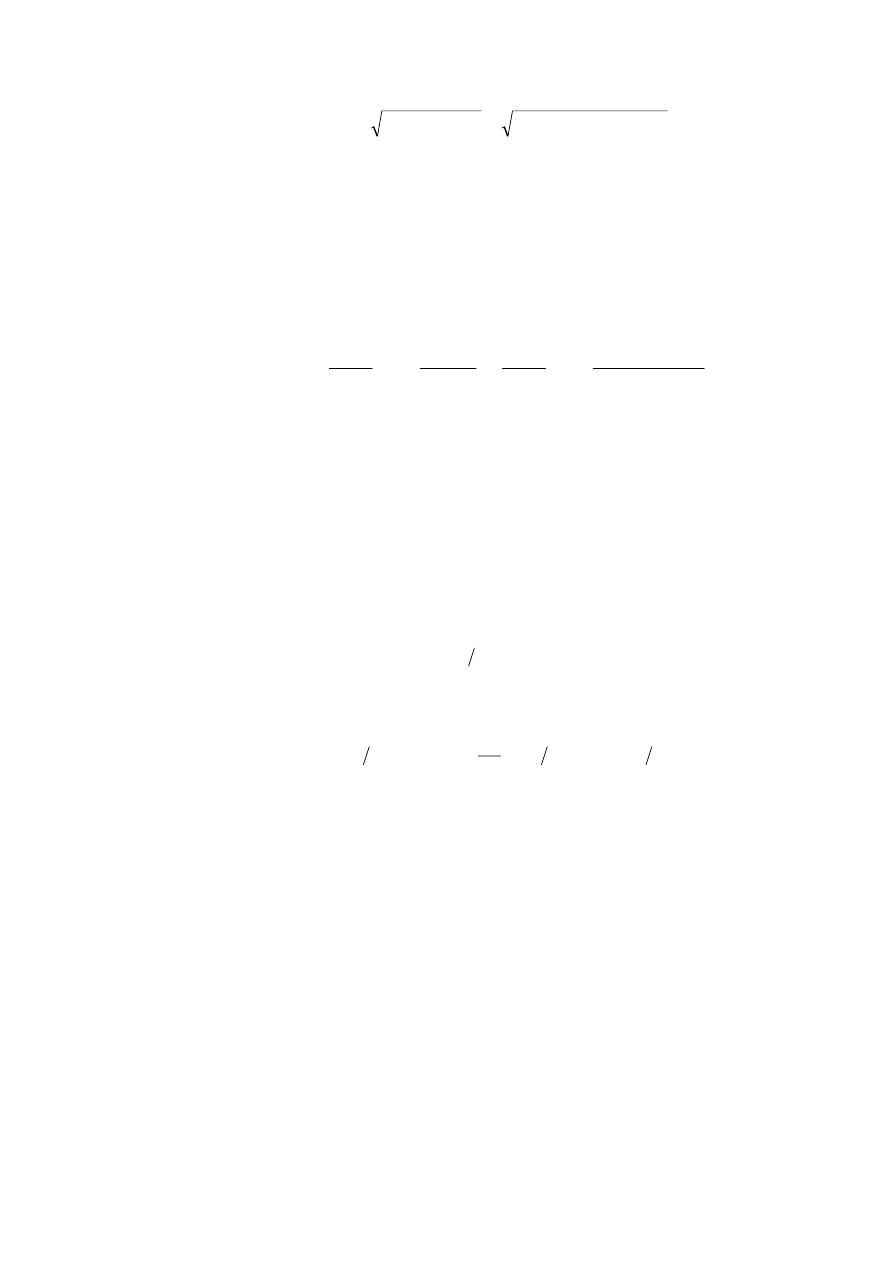
78
)
(
)
)
(
(
)
(
)
(
)
(
2
1
2
1
2
2
n
n
A
n
n
n
n
n
n
n
Z
s
c
s
c
+
−
=
+
=
(4.15)
Jak widać, jej rozkład można policzyć korzystając z wyżej przedstawionej
metody wstawiając w miejsce zmiennych losowych I i Q odpowiednio n
c1
i n
s1
,
z tym, że jedna ze zmiennych (jeśli ich rozkłady są takie same, to nie ma
znaczenia która) ma wartość średnią równą energii/amplitudzie sygnału echa.
Jeśli zmienne losowe n
c
i n
s
mają rozkład Gaussa, to ich łączny rozkład można
zapisać poniższą zależnością:
)
2
)
(
exp(
2
1
)
2
exp(
2
1
)
,
(
2
2
1
2
1
2
2
2
2
2
1
1
,
w
s
c
w
w
s
c
w
s
c
ns
nc
n
A
n
n
n
n
n
p
σ
πσ
σ
πσ
+
−
−
=
+
−
=
(4.16)
Należy zauważyć, że uzyskane rozkłady dla przypadku, gdy prawdziwa
jest hipoteza H
1
są tak naprawdę rozkładami warunkowymi, gdyż ich postać
zależy od rozkładu fazy sygnału użytecznego
β
(ogólnie od wszystkich
losowych parametrów rozkładu). Aby uniezależnić się od fazy należy uśrednić
rozkłady po wszystkich wartościach
β
. Niestety w tym momencie niezbędna jest
znajomość rozkładu prawdopodobieństwa fazy p(
β
). Znając go, aby uzyskać
rozkład bezwarunkowy należy obliczyć poniższą całkę:
∫
⋅
=
π
β
β
β
2
0
)
(
)
(
)
(
d
p
Z
p
Z
p
(4.17)
Jeśli przyjąć najmniej korzystny, czyli równomierny rozkład fazy, to
)
(
)
(
2
1
)
(
)
(
)
(
2
0
2
0
β
β
β
π
β
β
β
π
π
Z
p
d
Z
p
d
p
Z
p
Z
p
∫
∫
=
⋅
=
⋅
=
(4.18)
i wtedy postać rozkładu zmiennej Z nie ulega zmianie.
Opierając się na powyższej metodzie napisano funkcję działającą w
środowisku MATLAB, obliczającą rozkład prawdopodobieństwa obwiedni
sygnału za detektorem fazy, czyli rozkład zmiennej losowej równej
pierwiastkowi kwadratowemu z sumy kwadratów dwóch zmiennych losowych X
i Y. Prototyp funkcji zapisany jest poniżej:
[p]=sqrtpdf(x, 'fun1', 'fun2', arg1_fun1, arg1_fun2, arg2_fun1, ...)
Zmienna
x
jest wektorem wartości zmiennych losowych X i Y, zaś
fun1
i
fun2
nazwami funkcji generujących rozkłady tych dwóch zmiennych:.p
X
(x) i p
Y
(x).
Dalej podawane są dodatkowe argumenty dla
fun1
i
fun2
jak np. średnia i
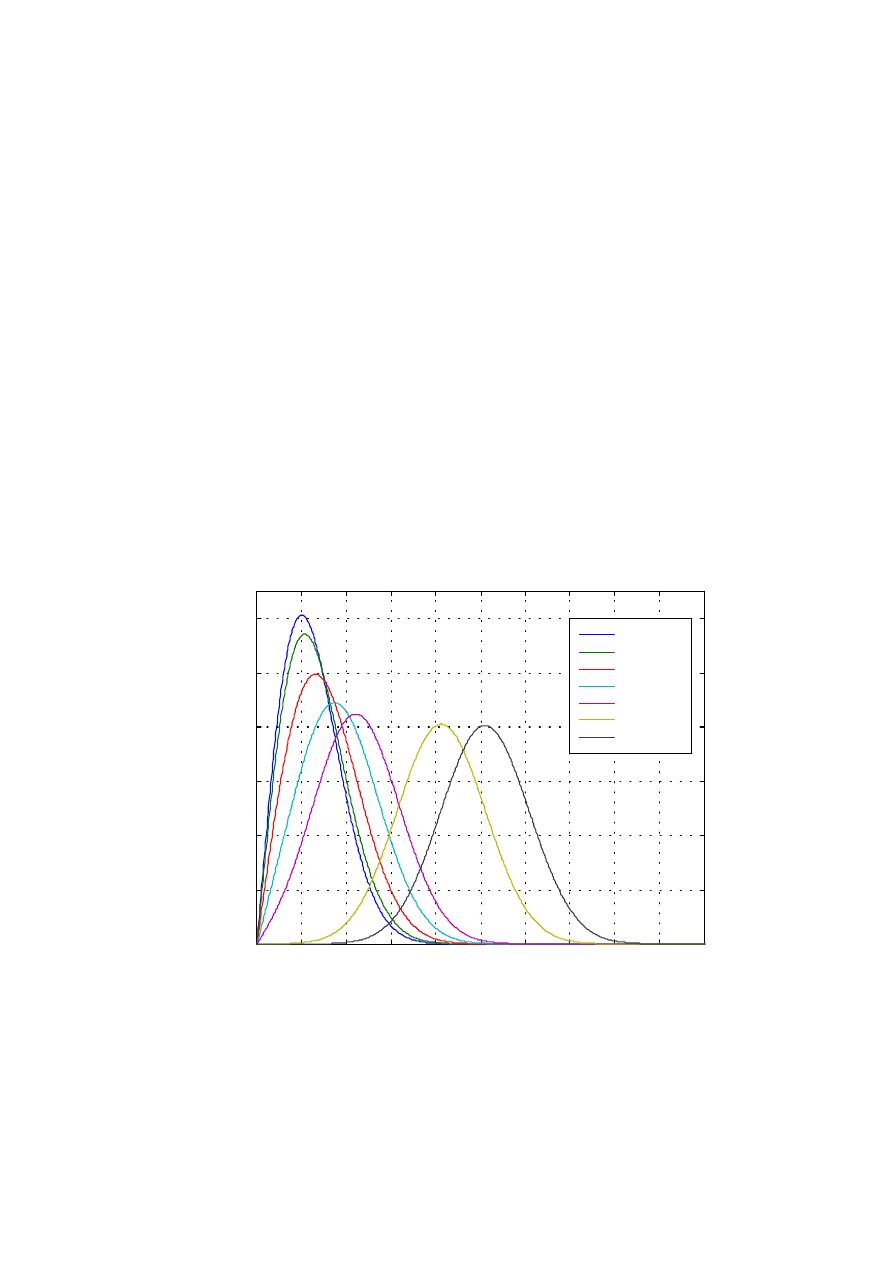
79
wariancja. Przykładowe poniższe wywołanie wyliczy gęstość rozkładu
prawdopodowbieństwa Rice’a o parametrach
σ
=1 oraz A=10:
x=[0:0.125:30]’;
[p]=sqrtpdf(x,'normpdf','normpdf',0,1,10,1);
Funkcja
normpdf
jest częścią pakietu statystycznego i wylicza wartości
rozkładu normalnego zgodnie z ogólnie znanym wzorem. Na wykresie 4.2
pokazano przykładowe krzywe rozkładów Rice’a/Rayleya uzyskane funkcją
sqrtpdf
dla różnych wartości parametru A. Jeśli w układzie jest filtr
dopasowany i przyjąć moc szumu za nim
σ
w
2
równą 1, to wartości A równe są
napięciowemu stosunkowi Sygnał/Szum sygnału odebranego przez antenę
radaru. Na kolejnym wykresie 4.3 pokazano błąd bezwzględny wartości
rozkładów uzyskanych funkcją
sqrtpdf
i bezpośrednio ze wzoru na rozkład
Rice’a.
0
1
2
3
4
5
6
7
8
9
10
0
0.1
0.2
0.3
0.4
0.5
0.6
x
p(x
)
S/N=0,0
S/N=0,5
S/N=1,0
S/N=1,5
S/N=2,0
S/N=4,0
S/N=5,0
Rys. 4.2. Krzywe rozkładów prawdopodobieństwa uzyskane funkcją
sqrtpdf
dla wybranych
wartości stosunku Sygnał/Szum. Dla S/N=0 rozkład Rayleya
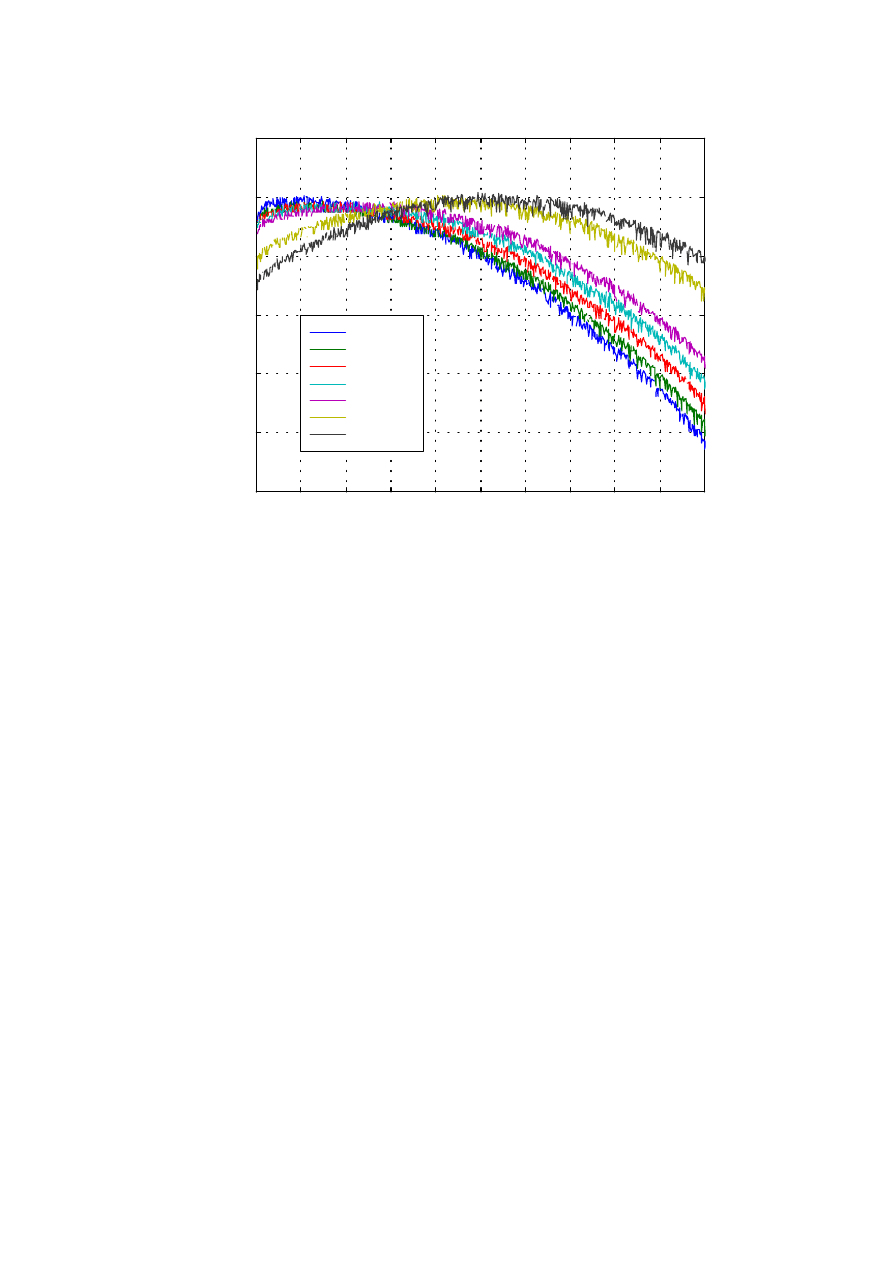
80
0
1
2
3
4
5
6
7
8
9
10
10
-40
10
-35
10
-30
10
-25
10
-20
10
-15
10
-10
x
|p
(x
)-p
1(x
)|
S/N=0,0
S/N=0,5
S/N=1,0
S/N=1,5
S/N=2,0
S/N=4,0
S/N=5,0
Rys. 4.3. Błąd bezwzględny wartości rozkładów uzyskanych funkcją
sqrtpdf
i bezpośrednio
ze wzoru na rozkład Rice’a
Błąd wynika głównie z tego, że aby uzyskać szukany rozkład należy wykonać
całkowanie rozkładu dwuwymiarowego, która to operacja wprowadza błędy w
obliczeniach. Wszystkie całki były liczone z zastosowaniem metody trapezów
standardową funkcją MATLABA
trapz
[7, 14].
Mając rozkłady prawdopodobieństwa dla różnych wartości S/N można
wykreślić charakterystyki detekcji. Wykonuje to funkcja
detect
, której sposób
wywołanie pokazany jest poniżej:
[d, sn]=detect(x, p, pfalse, snmax)
Jako argumenty przyjmuje:
x
, czyli wektor wartości zmiennej losowej, macierz
p
, w której każda kolumna zawiera wartości krzywych rozkładu dla różnych
wartości S/N, prawdopodobieństwo fałszywego alarmu (
pfalse
), oraz
maksymalną wartość S/N (
snmax
). Funkcja najpierw wylicza “odwrotne”
dystrybuanty rozkładów, czyli prawdopodobieństwa, że sygnał przekroczy
pewną wartość progową, a następnie wylicza i zwraca na wyjście wektor
wartości S/N (równomiernie rozłożone wartości od zera do
snmax
) oraz wektor
prawdopodobieństw detekcji dla założonej wartości
pfalse
. Na kolejnych
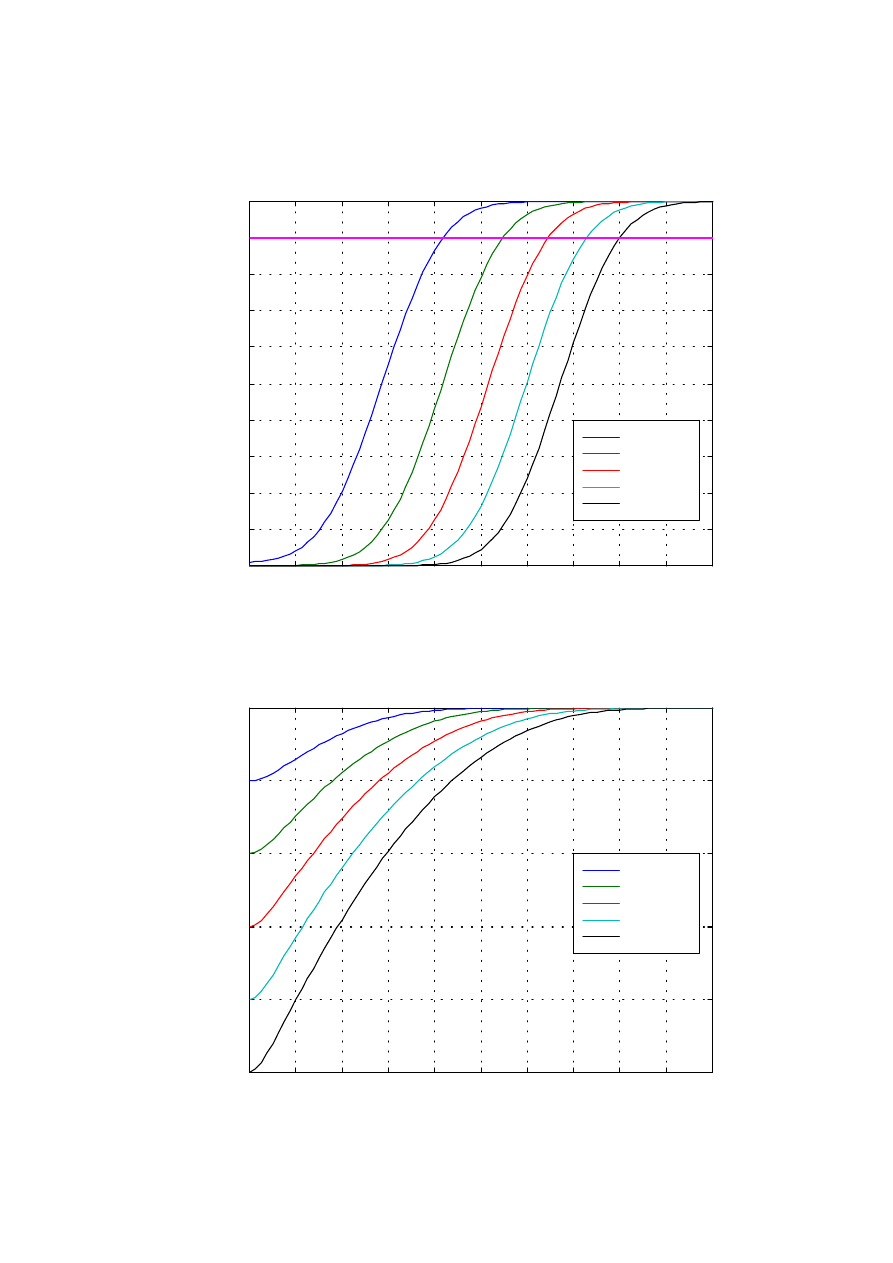
81
wykresach 4.4a,b pokazano uzyskane tą funkcją przykładowe krzywe detekcji
dla różnych wartości F w skali liniowej (a) i logarytmicznej (b).
0
1
2
3
4
5
6
7
8
9
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-2
F=1e-4
F=1e-6
F=1e-8
F=1e-10
Rys. 4.4a. Charakterystyki detekcji pojedynczego impulsu dla różnych wartości F (skala liniowa)
0
1
2
3
4
5
6
7
8
9
10
10
-10
10
-8
10
-6
10
-4
10
-2
10
0
S/N
D
F=1e-2
F=1e-4
F=1e-6
F=1e-8
F=1e-10

82
Rys. 4.4b. Charakterystyki detekcji pojedynczego impulsu dla różnych wartości F (skala
logarytmiczna)
4.2. ROZKŁADY SYGNAŁU ZA UKŁADEM CFAR
Obliczenie rozkładów prawdopodobieństw sygnału i charakterystyk
detekcji za układem stabilizacji fałszywego alarmu jest dość trudne. Niezależnie
od tego, którą z implementacji pokazanych w poprzednim rozdziale wybrać,
obliczenia polegają na znalezieniu najpierw funkcji gęstości
prawdopodobieństwa średniej z N próbek S
x
(czyli S
sr
), a następnie rozkład
zmiennej losowej S
wyj
=S
x
/S
sr
(gdzie S
x
ma rozkład Rayleya dla szumu lub
rozkład Rice’a dla sumy szumu i sygnału).
Pierwszym etapem jest znalezienie rozkładu zmiennej losowej S
sr
, która z
dokładnością do stałych współczynników jest sumą N zmiennych losowych S
x
.
Rozkład sumy zmiennych losowych równy jest splotowi rozkładów sumowanych
zmiennych. Aby szybko go znaleźć dla dużych N, to zamiast liczyć splot można
znaleźć funkcję charakterystyczną rozkładu p(S
x
), która jest jego transformatą
Fouriera, podnieść ją do N-tej potęgi, a następnie obliczyć odwrotną
transformatę [1, 8, 12]. Po odpowiednim przeskalowaniu uzyska się rozkład
p(S
sr
). Do obliczenia funkcji charakterystycznych metodami numerycznymi
można wykorzystać szybki algorytm FFT. Napisana dla MATLABA funkcja
sumpdf
w zależności od sposobu wywołania tzn.
[py y]=sumpdf(x, px, N, ’sum’)
[py y]=sumpdf(x, px, N, ’mean’)
oblicza albo rozkład sumy albo rozkład estymatora wartości średniej. Na
wykresie 4.5 pokazano przykładowe krzywe rozkładów wartości średniej z sumy
rozkładów Rayleya dla różnych N.
Znając rozkład średniej można określić rozkład zmiennej losowej S
wyj
.
Najpierw należy znaleźć łączny rozkład zmiennych S
x
i S
sr
. Ponieważ są one
niezależne (bo w liczeniu wartości S
sr
nie bierze udział komórka testowa), to
łączny rozkład równy jest
)
(
)
(
)
,
(
,
sr
Ssr
x
Sx
sr
x
Ssr
Sx
S
p
S
p
S
S
p
⋅
=
(4.19)
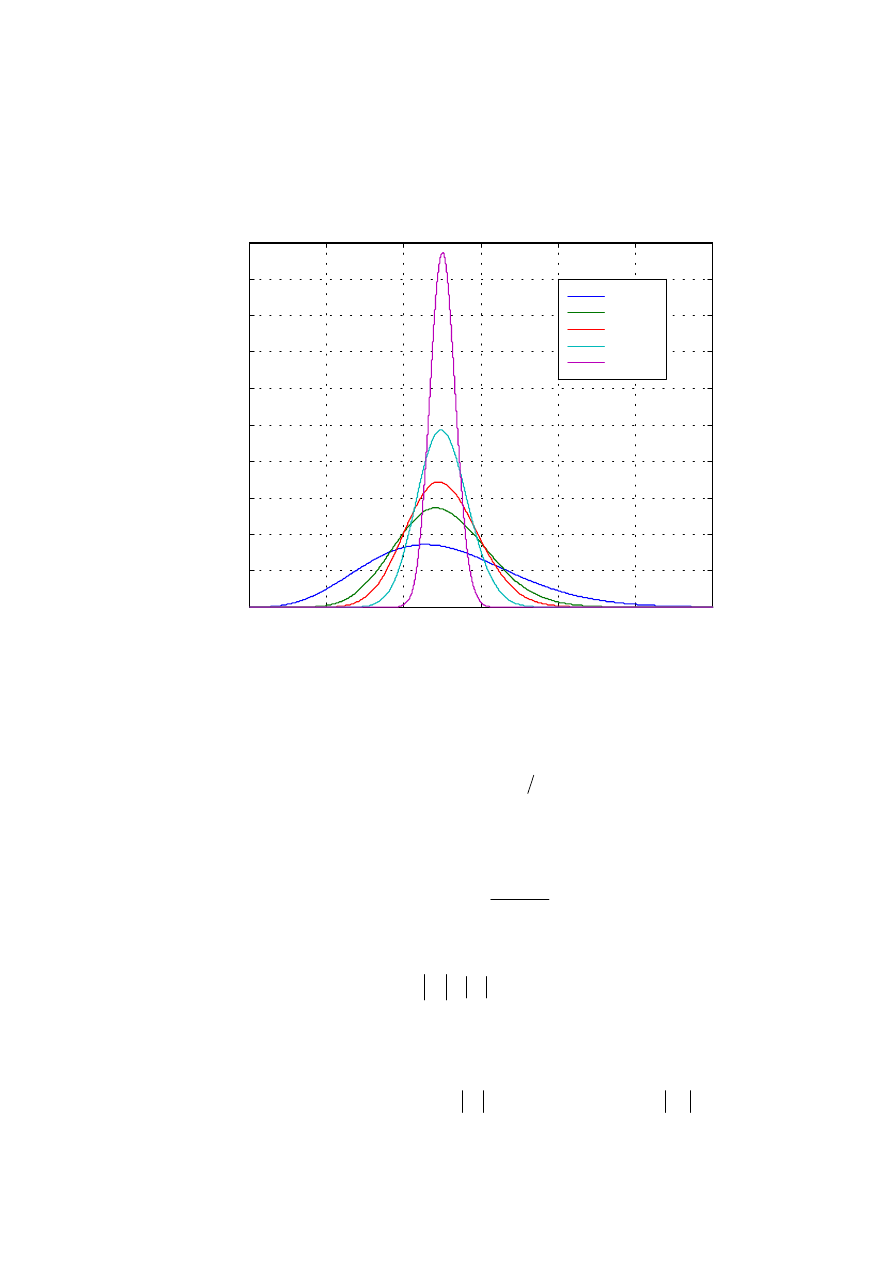
83
Wprowadzona zostanie nowa zmienna losowa
ξ
=S
sr
i wtedy można zapisać, że
=
sr
x
wyj
S
S
g
S
ξ
(4.20)
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
y
p(
y)
N=2
N=5
N=8
N=16
N=64
Rys. 4.5. Rozkłady prawdopodobieństw estymatorów wartości średnich dla rozkładu Rayleya o
parametrze
σ
=1
gdzie funkcja g:R
2
→
R
2
określona jest wzorem
=
2
2
1
2
1
x
x
x
x
x
g
(4.21)
Przekształcenie odwrotne g
-1
i jej pochodna mają postać jak poniżej [8]:
=
⋅
=
−
1
0
)
(
,
1
2
1
2
2
1
2
1
y
y
dy
y
dg
y
y
y
y
y
g
(4.22)
W związku z tym moduł jakobianu przekształcenia g
-1
równy jest
2
y
J
g
=
(4.23)
i ostatecznie łączny rozkład gęstości prawdopodobieństwa zmiennych losowych
S
wyj
i S
sr
można zapisać:
sr
sr
Ssr
sr
x
Sx
Ssr
Sx
Ssr
Swyj
S
S
p
S
S
p
y
y
y
y
p
y
y
p
⋅
⋅
=
⋅
=
)
(
)
(
)
,
(
)
,
(
2
2
2
1
,
2
1
,
(4.24)
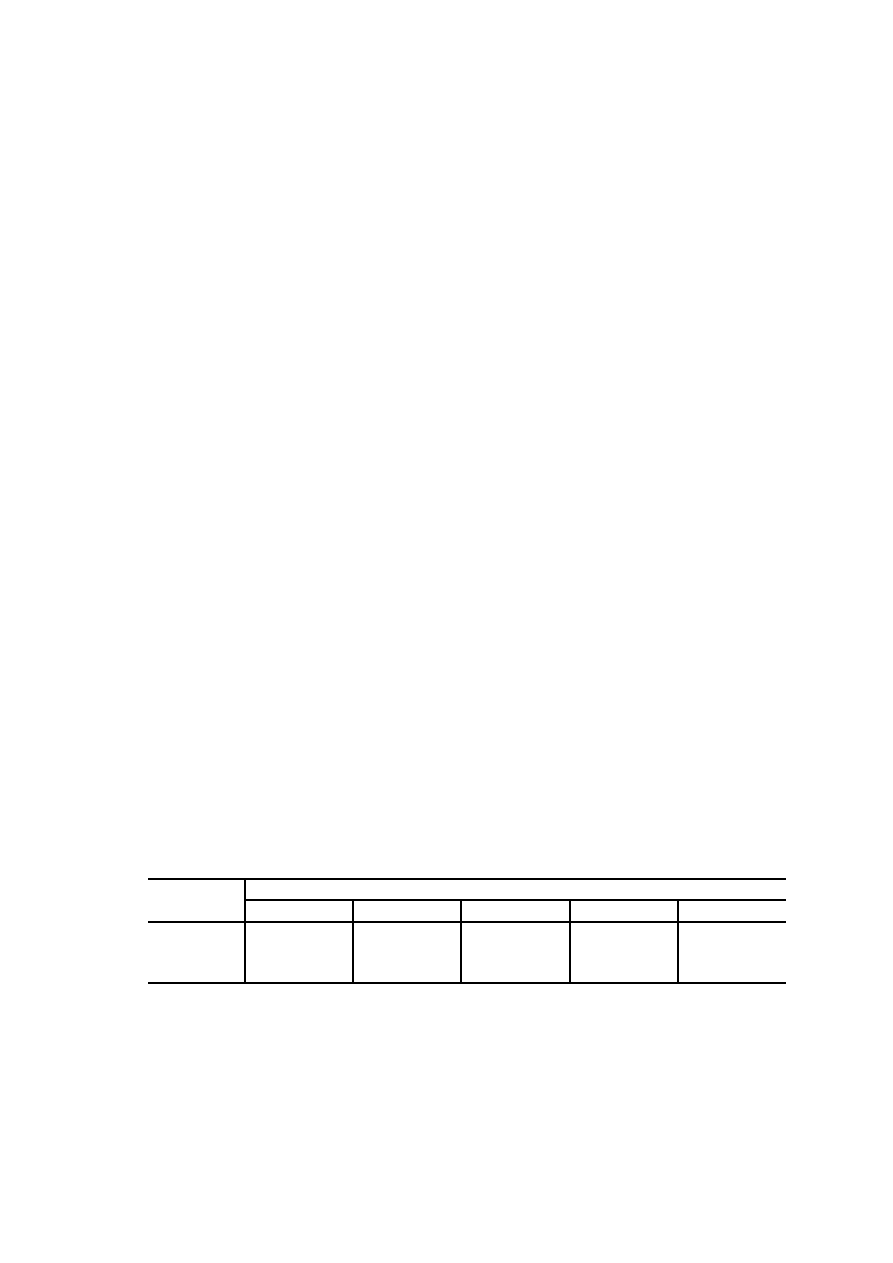
84
Rozkład brzegowy zmiennej losowej S
wyj
uzyska się całkując gęstość
p
Swyj,Ssr
(y
1
,y
2
) względem y
2
:
∫
=
2
2
1
,
1
)
,
(
)
(
dy
y
y
p
y
p
Ssr
Swyj
Swyj
(4.25)
Opierając się na powyższej metodzie napisano funkcję
normaliz
działającą w środowisku MATLAB, obliczającą rozkład prawdopodobieństwa
ilorazu zmiennych losowych, czyli też rozkład zmiennej losowej S
wyj
. Prototyp
funkcji zapisany jest poniżej:
[p]=normaliz(x, m, ’fun’, arg1_fun, arg2_fun, ...)
Zmienna
x
jest wektorem wartości obu dzielonych przez siebie zmiennych
losowych,
m
wektorem wartości rozkładu zmiennej z mianownika (np. uzyskany
za pomocą funkcji
sumpdf
), zaś
fun
nazwą funkcji generującej rozkład
zmiennej z licznika. Dalej podawane są dodatkowe argumenty dla
fun
.
Uzyskawszy rozkłady zmiennych losowych S
wyj
dla różnych wartości
stosunku Sygnał/Szum można za pomocą funkcji
detect
wyliczyć
charakterystyki wykrywania dla różnych wartości F. Przykładowe krzywe
pokazane są na czterech kolejnych wykresach 4.6a,b,c,d. W tabeli 4.1 poniżej
zestawiono straty, jakie wprowadza układ stabilizacji fałszywego alarmu dla
wybranych wartości F i różnych ilości N referencyjnych komórek
odległościowych dla D=0,9.
Tab. 4.1. Straty w dB wprowadzane przez układ CFAR dla D=0,9. Puste miejsce oznacza, że
dana krzywa w zakresie S/N=[0;20] nie osiągnęła wartości 0,9
N
F
2
5
8
16
64
10
-2
3,198
1,173
0,718
0,350
0,085
10
-4
−
2,506
1,497
0,719
0,177
10
-6
−
3,956
2,330
1,100
0,265
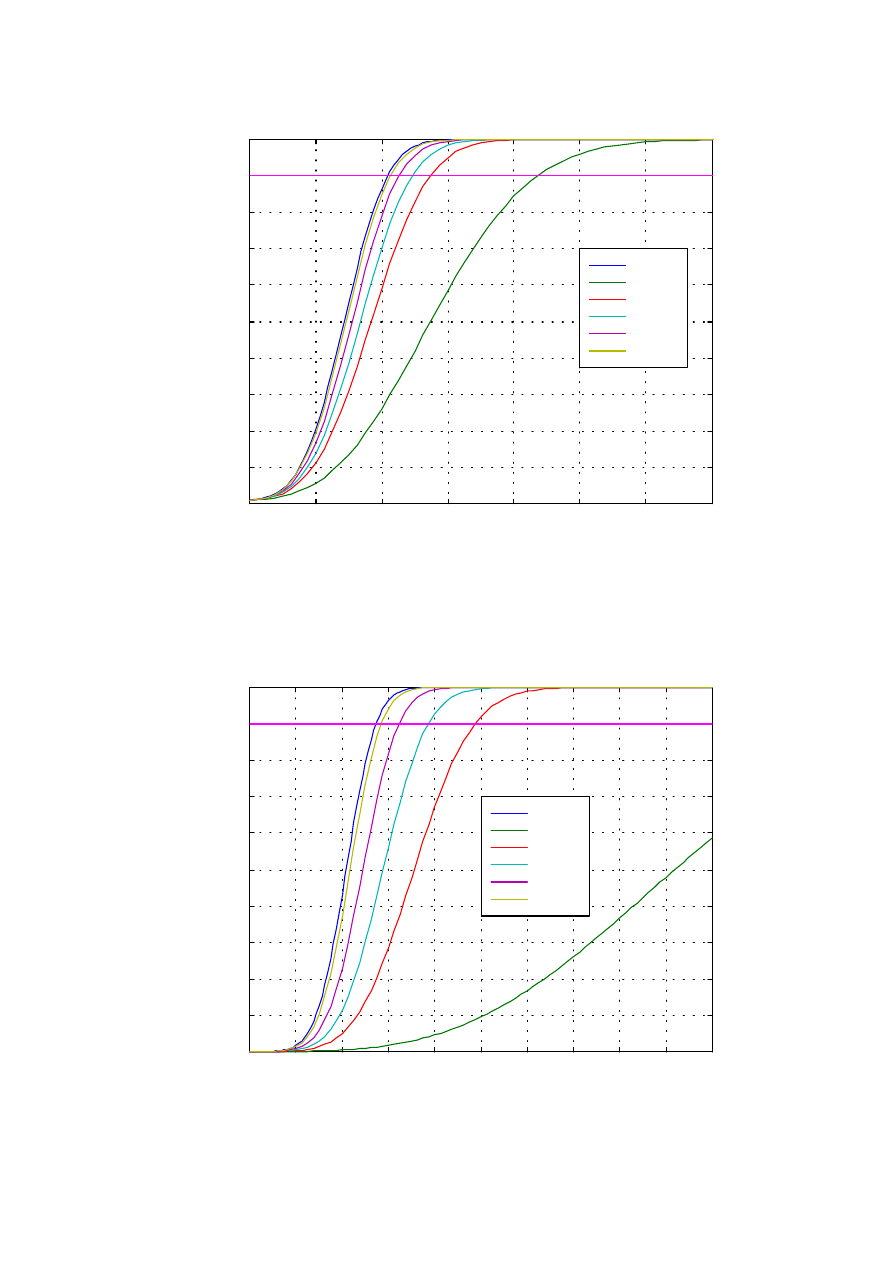
85
0
2
4
6
8
10
12
14
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-2
N=0
N=2
N=5
N=8
N=16
N=64
Rys. 4.6a. Charakterystyki detekcji pojedynczego impulsu za układem CFAR dla F=10
-2
i
różnych wartości N. N=0 oznacza brak układu CFAR
0
2
4
6
8
10
12
14
16
18
20
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-4
N=0
N=2
N=5
N=8
N=16
N=64
Rys. 4.6b. Charakterystyki detekcji pojedynczego impulsu za układem CFAR dla F=10
-4
i
różnych wartości N. N=0 oznacza brak układu CFAR
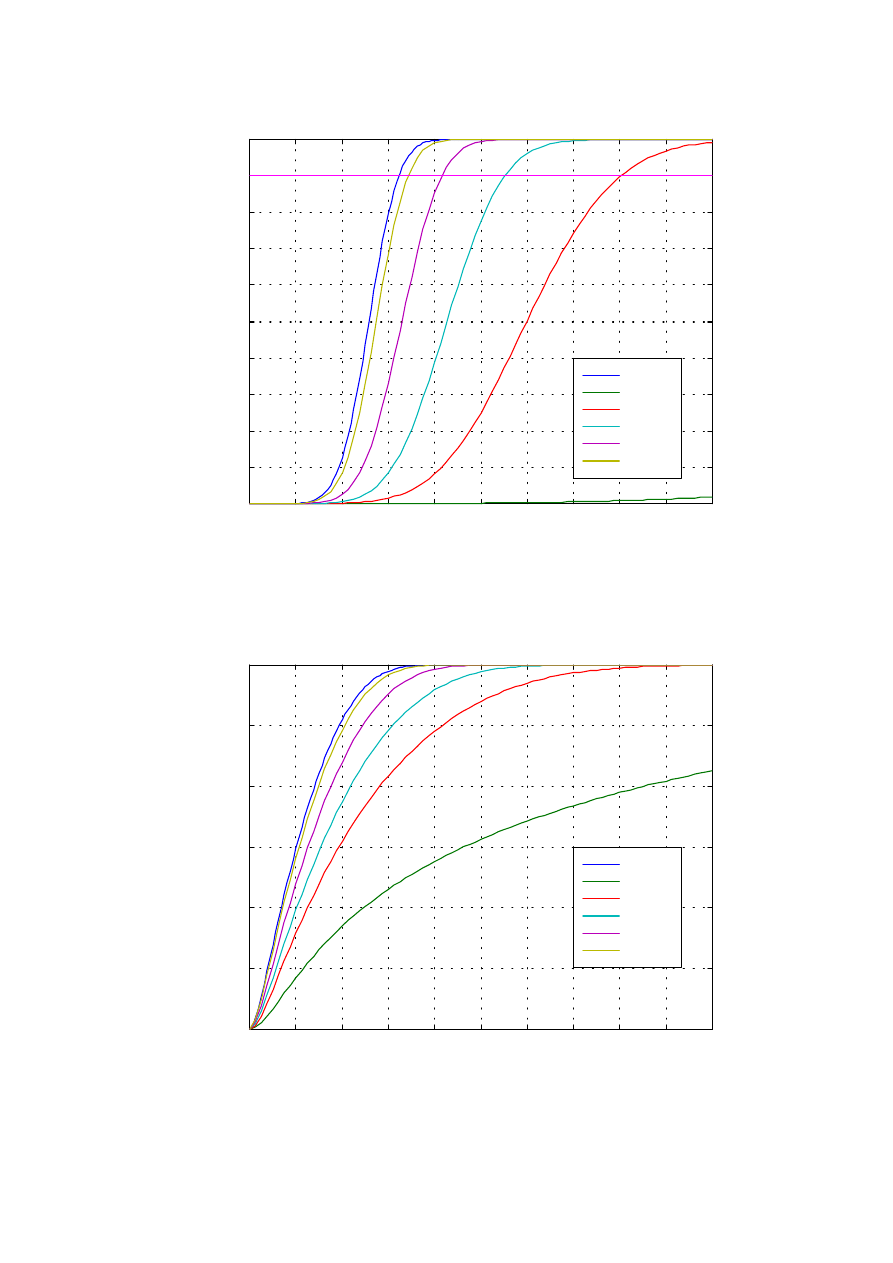
86
0
2
4
6
8
10
12
14
16
18
20
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-6
N=0
N=2
N=5
N=8
N=16
N=64
Rys. 4.6c. Charakterystyki detekcji pojedynczego impulsu za układem CFAR dla F=10
-6
i
różnych wartości N (skala liniowa). N=0 oznacza brak układu CFAR
0
2
4
6
8
10
12
14
16
18
20
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
S/N
D
F=1e-6
N=0
N=2
N=5
N=8
N=16
N=64
Rys. 4.6d. Charakterystyki detekcji pojedynczego impulsu za układem CFAR dla F=10
-6
i
różnych wartości N (skala logarytmiczna). N=0 oznacza brak układu CFAR

87
Jak widać z wartości w tabeli im większa ilość N komórek referencyjnych brana
jest do liczenia średniej, tym straty CFAR są mniejsze i charakterystyka detekcji
bliższa jest tej , gdy nie ma układu CFAR. Im większe N, tym rozkład zmiennej
losowej S
sr
bardziej jest skupiony wokół swojej wartości centralnej (patrz wykres
4.5). Dla dużych wartości N dzielenie zmiennych losowych S
x
/S
sr
sprowadza się
praktycznie do przeskalowania zmiennej S
x
przez stałą wartość, a ta operacja
nie zmieni kształtu rozkładu zmiennej S
wyj
w stosunku do S
x
. Co za tym idzie
charakterystyki detekcji będą takie, jak przy braku układu CFAR. Niestety nie
można brać zbyt dużego N, ponieważ równałoby się to przyjęciu błędnego
założenia, że poziom clutteru jest stały w dużym obszarze przestrzeni, a nie
tylko lokalnie wokół testowanej komórki odległościowej. Dobrą praktyczną
zasadą jest użycie takiej liczby komórek odniesienia, aby utrzymać straty CFAR
poniżej 1dB [11]. Przyglądając się tabeli 4.1 widać, że dla prawdopodobieństwa
fałszywego alarmu F=10
-2
wystarczy już 8 komórek referencyjnych, natomiast
dla F=10
-4
i F=10
-6
wystarczy N równe około 16.
4.3. ROZKŁADY SYGNAŁU ZA INTEGRATOREM BINARNYM
Aby określić prawdopodobieństwo detekcji oraz fałszywego alarmu
integratora binarnego lub rozkłady za integratorem, trzeba znać odpowiednie
wartości i rozkłady dla pojedynczego impulsu. Integrator binarny integruje
paczki po N impulsów, zaś wykryje tylko te paczki, dla których liczba impulsów k
przekraczających próg będzie równa lub większa od założonej przez
obserwatora liczby M. Dla każdego k możliwych jest
!
)!
(
!
k
k
N
N
k
N
−
=
(4.26)
takich paczek. Jeśli prawdopodobieństwo przekroczenia
wartości progowej przez dowolny impuls oznaczyć przez
D
0
, zaś prawdopodobieństwo fałszywego przekroczenia

88
(alarmu) przez F
0
, to prawdopodobieństwo, że dokładnie k
impulsów z N przekroczy próg (mówiąc ogólnie będzie k
sukcesów w N niezależnych próbach) dane jest wzorem na
prawdopodobieństwo w tzw. schemacie Bernouliego [12]:
k
N
k
N
D
D
k
N
k
P
−
−
=
)
1
(
)
(
0
0
(4.27)
Liczba D
0
jest prawdopodobieństwem detekcji pojedynczego impulsu, czyli
sukcesu w pojedynczej próbie, a (1-D
0
) prawdopodobieństwem przeoczenia
impulsu, czyli inaczej mówiąc porażki w pojedynczej próbie. W związku z
powyższym prawdopodobieństwo detekcji (przekroczenia progu) przez M i
więcej impulsów wynosi:
∑
=
−
−
=
N
M
k
k
N
k
D
D
k
N
D
)
1
(
0
0
(4.28)
Dla M=0 zawsze D=1, ponieważ ze wzoru (4.28) wynika, że
[
]
1
)
1
(
0
0
=
−
+
N
D
D
Analogicznie całe prawdopodobieństwo fałszywego
alarmu to znaczy prawdopodobieństwo, że M i więcej
zakłóceń przekroczy próg) wynosi:
∑
=
−
−
=
N
M
k
k
N
k
F
F
k
N
F
)
1
(
0
0
(4.29)
jednak musi być M>0. W przeciwnym przypadku F wyniesie 1. Korzystając z
powyższego wzoru i znając prawdopodobieństwa zdarzeń polegających na tym,
że sygnał przekroczy pewną wartość progową X
0
tzn. P(x>X
0
) dla pojedynczego
impulsu, można także określić prawdopodobieństwo, że M i więcej impulsów
przekroczy próg:
∑
=
−
−
>
−
>
=
>
N
M
k
k
N
k
M
N
X
x
P
X
x
P
k
N
X
x
P
))
(
1
(
)
(
)
(
0
0
0
(4.30)
Wartości D
0
i F
0
występujące w poprzednich wyrażeniach można znaleźć z
krzywych detekcji dla pojedynczego impulsu z przypadkową fazą początkową
89
(wykresy 4.4a, 4.4b). Przy czym jeżeli energia całej paczki wynosi E, to w celu
wyznaczenia D
0
z charakterystyk detekcji należy wziąć energię E/N.
Mając rozkłady prawdopodobieństw pojedynczego impulsu dla różnych
wartości S/N można wykreślić charakterystyki detekcji. Wykonuje to funkcja
binint
, której sposób wywołanie pokazany jest poniżej:
[d, sn]=binint(x, p, N, M, pfalse, snmax)
Funkcja jest oparta na wcześniej opisanej funkcji
detect
. Jako argumenty
przyjmuje:
x
, czyli wektor wartości zmiennej losowej, macierz
p
, w której każda
kolumna zawiera wartości krzywych rozkładu dla różnych wartości S/N,
parametry integratora binarnego (
N
z
M
), prawdopodobieństwo fałszywego
alarmu (
pfalse
), oraz maksymalną wartość S/N (
snmax
). Funkcja najpierw
wylicza odwrotne dystrybuanty rozkładów, czyli prawdopodobieństwa, że sygnał
przekroczy pewną wartość progową, potem każdą wartość
prawdopodobieństwa modyfikuje w oparciu o wzór na schemat Bernouliego, a
następnie wylicza i zwraca na wyjście wektor wartości S/N (równomiernie
rozłożone wartości od zera do
snmax
) oraz wektor prawdopodobieństw detekcji
dla założonej wartości
pfalse
. Dalej na kolejnych wykresach 4.7a,b,c,d
pokazano uzyskane tą funkcją przykładowe krzywe detekcji dla różnych
wartości F, N oraz M. W tabelach 4.2a,b dla przykładu zestawiono zysk z
integracji dla integratora binarnego w stosunku do detekcji pojedynczego
impulsu dla D=0,9. Pogrubieniem zaznaczono najlepszy integrator na tym
poziomie prawdopodobieństwa detekcji. Na wykresie 4.8 dla lepszego
uwidocznienia została pokazana zawartość tabel 4.2a,b.
Tab. 4.2a. Zysk w dB z zastosowania integratora binarnego dla N=10, D=0,9
Zysk w dB dla N=10, D=0,9
M
F=10
-6
F=10
-4
1
1.321
1.513
2
2.474
2.556
3
2.986
2.992
4
3.236
3.192
5
3.362
3.261
6
3.390
3.254
7
3.346
3.178
8
3.204
3.004
9
2.934
2.686
10
2.331
2.020
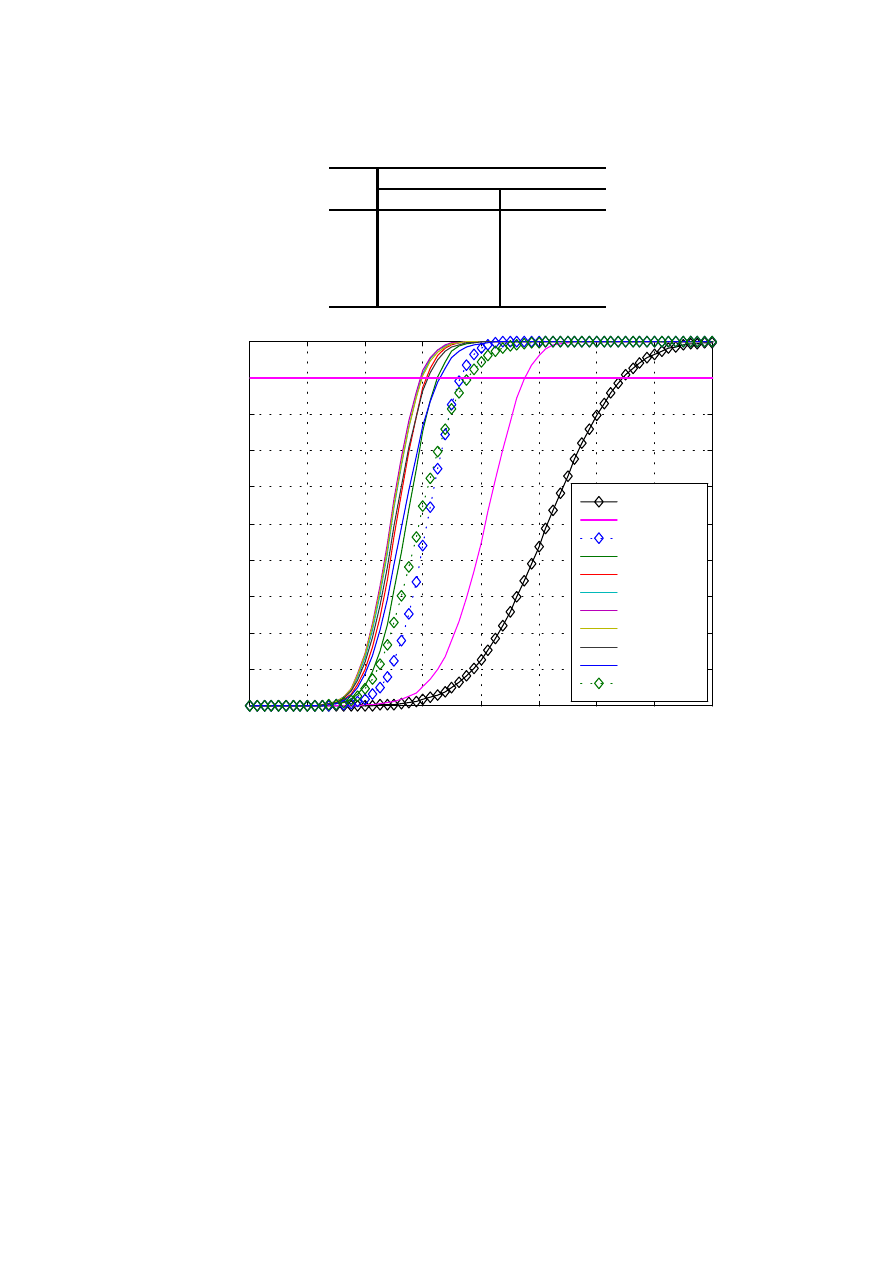
90
Tab. 4.2b. Zysk w dB z zastosowania integratora binarnego dla N=5, D=0,9
Zysk w dB dla N=5, D=0,9
M
F=10
-6
F=10
-4
1
1.000
1.141
2
1.965
1.990
3
2.273
2.213
4
2.256
2.124
5
1.835
1.616
0
1
2
3
4
5
6
7
8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-6, N=10
N=1, M=1
M=1
M=2
M=3
M=4
M=5
M=6
M=7
M=8
M=9
M=10
Rys. 4.7a. Charakterystyki detekcji integratora binarnego dla F=10
-6
i N=10. Krzywa N=1,M=1
jest charakterystyką dla pojedynczego impulsu
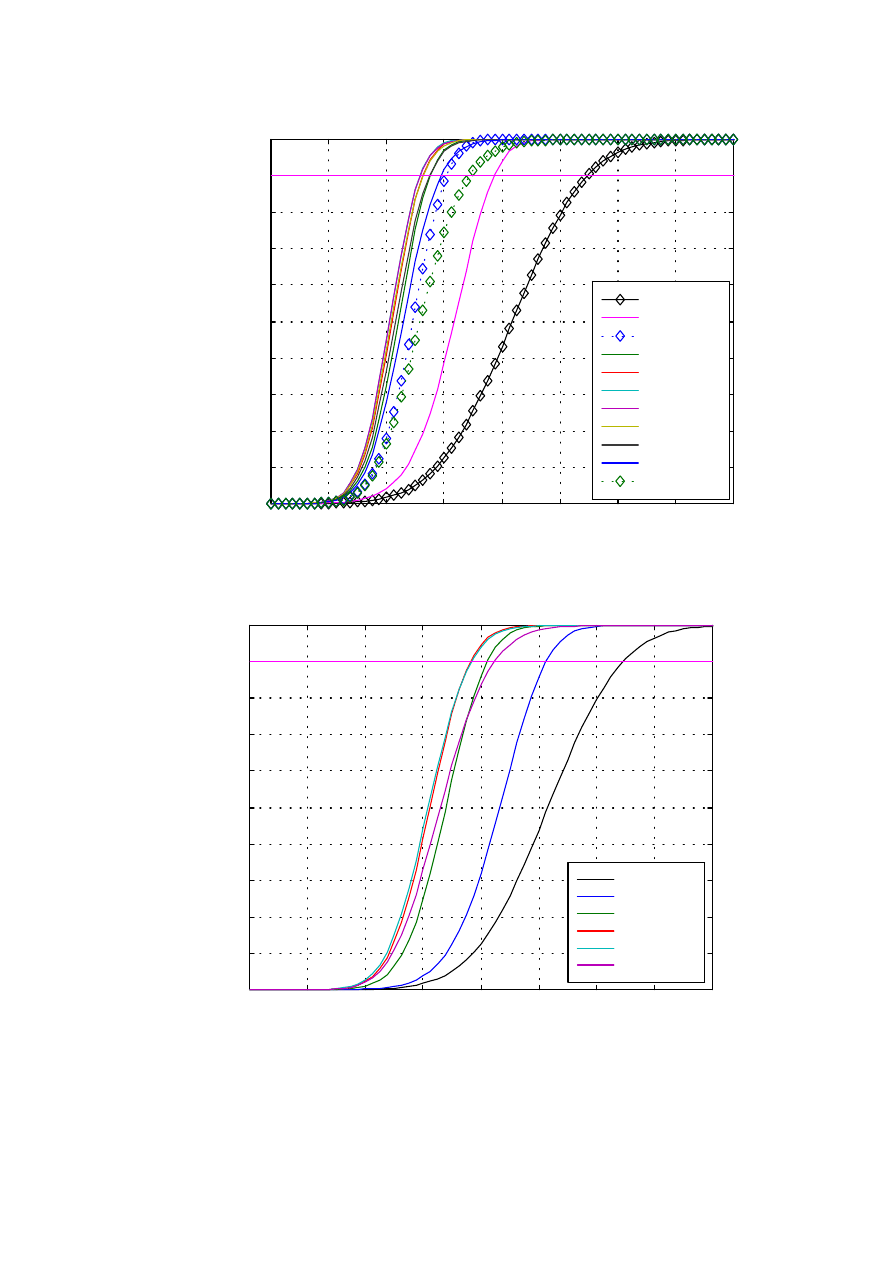
91
0
1
2
3
4
5
6
7
8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-4, N=10
N=1, M=1
M=1
M=2
M=3
M=4
M=5
M=6
M=7
M=8
M=9
M=10
Rys. 4.7b. Charakterystyki detekcji integratora binarnego dla F=10
-4
i N=10. Krzywa N=1,M=1
jest charakterystyką dla pojedynczego impulsu
0
1
2
3
4
5
6
7
8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-6, N=5
N=1, M=1
M=1
M=2
M=3
M=4
M=5
Rys. 4.7c. Charakterystyki detekcji integratora binarnego dla F=10
-6
i N=5. Krzywa N=1,M=1
jest charakterystyką dla pojedynczego impulsu
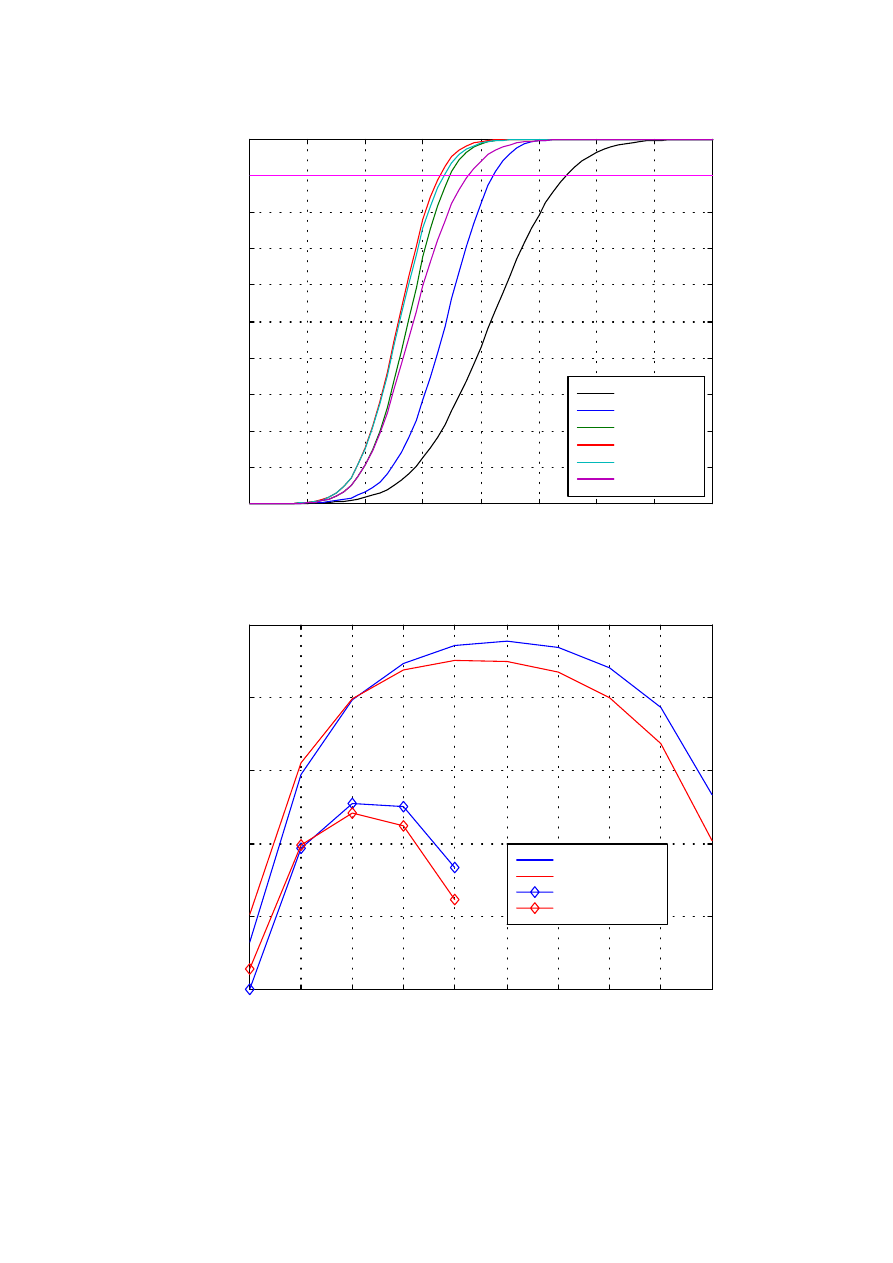
92
0
1
2
3
4
5
6
7
8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-4, N=5
N=1, M=1
M=1
M=2
M=3
M=4
M=5
Rys. 4.7d. Charakterystyki detekcji integratora binarnego dla F=10
-4
i N=5. Krzywa N=1,M=1
jest charakterystyką dla pojedynczego impulsu
1
2
3
4
5
6
7
8
9
10
1
1.5
2
2.5
3
3.5
M
Zy
sk
w
d
B
Zysk w dB z integracji w stosunku do detekcji jednego impulsu dla D=0,9
F=1e-6, N=10
F=1e-4, N=10
F=1e-6, N=5
F=1e-4, N=5
Rys. 4.8. Zysk w dB z zastosowania integratora binarnego w stosunku do detekcji
pojedynczego impulsu dla D=0,9 i różnych wartości F, N

93
4.4. ROZKŁADY SYGNAŁU ZA INTEGRATOREM DZIAŁAJĄCYM
BEZPOŚREDNIO NA AMPLITUDZIE
Analiza integratora działającego bezpośrednio na amplitudzie sygnału i
sumującego impulsy będzie podzielona na dwie części, gdyż w zależności od
poziomu sygnału można mówić o dwóch różnych urządzeniach.
Zgodnie z tym, co powiedziano w punkcie 3.3 jeśli amplituda impulsu jest
duża w porównaniu szumami, integrator sumuje impulsy zgodnie z poniższym
wyrażeniem:
∑
i
i
i
Z
S
2
0
σ
Jeśli amplituda impulsu jest skrajnie mała lepiej integrator liniowy zastąpić
kwadratowym:
∑
i
i
i
Z
S
4
2
0
2
4
σ
W obu wyrażeniach
σ
jest odchyleniem standardowym szumu na wejściu
integratora, zaś S
i
współczynnikami wagowymi mającymi zniwelować
modulację paczki przez charakterystykę anteny radaru.
W przypadku detektora liniowego sytuacja jest dość prosta. Aby znaleść
rozkład prawdopodobieństwa sumy zmiennych losowych o takich samych
rozkładach, który równy jest splotowi rozkładów sumowanych zmiennych,
należy postąpić podobnie, jak przy analizie układu CFAR, gdy liczyło się rozkład
średniej. Zamiast wykonywać wiele operacji splotów, należy skorzystać z
przekształcenia rozkładu na funkcję charakterystyczną. Takie sumowanie
wykonuje funkcja
sumpdf
.
Aby znaleźć rozkład sygnału za integratorem kwadratowym najpierw
należy obliczyć rozkład zmiennej losowej Y=X
2
, gdzie X o rozkładzie p
X
(x) jest
sygnałem przed integratorem. Skoro przekształcenie g:R
→
R ma postać
( )
2
x
x
g
=
(4.31)
to przekształcenie odwrotne i jej pochodna mogą być zapisane jak poniżej [5]:
( )
y
dy
y
dg
y
y
g
2
1
)
(
,
1
=
=
−
(4.32)
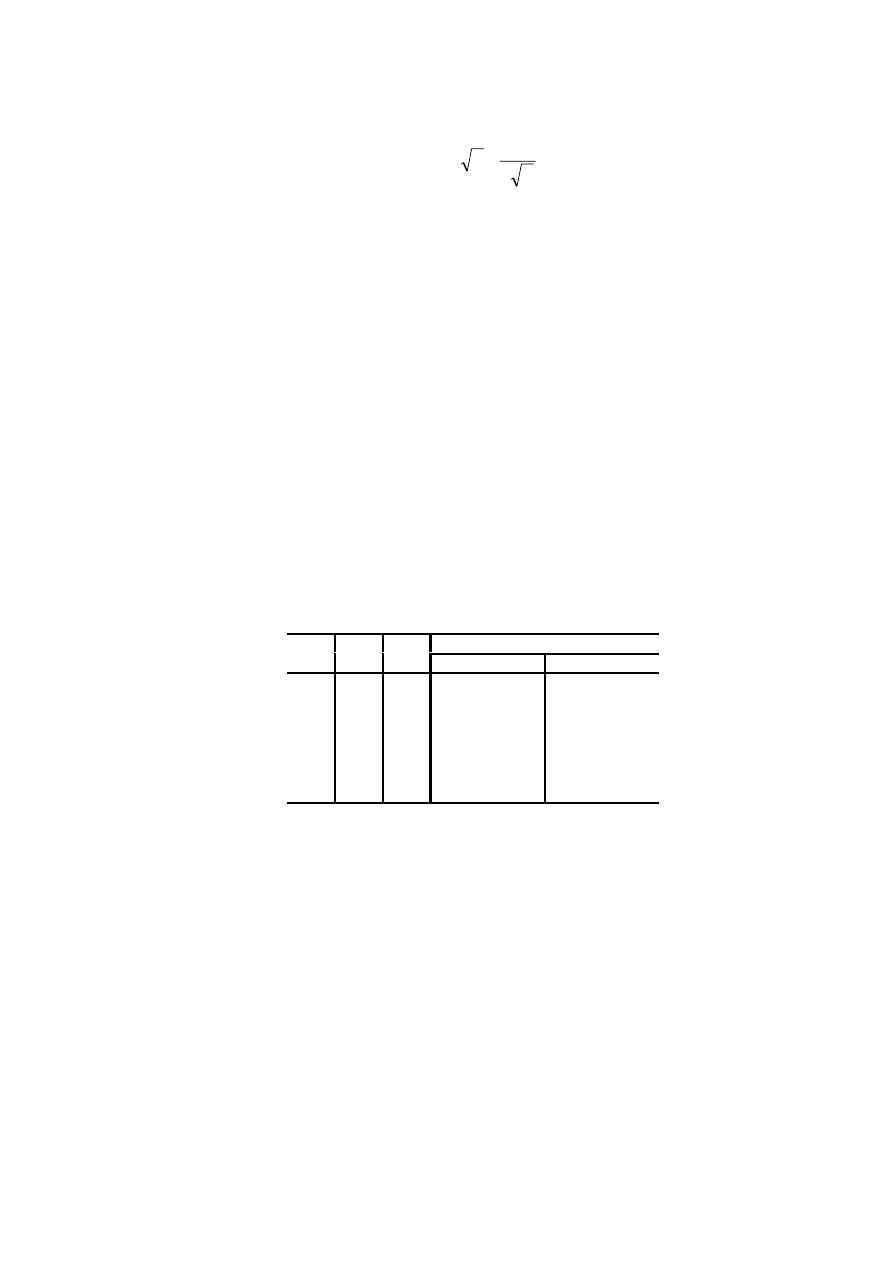
94
Rozkład prawdopodobieństwa zmiennej losowej Y równy jest:
y
y
p
y
p
X
Y
2
1
)
(
)
(
⋅
=
(4.33)
Można go uzyskać np. za pomocą funkcji
sqrtpdf
podstawiając zamiast x
pierwiastek kwadratowy z x i wynik funkcji mnożąc jak w wyrażeniu powyżej.
Mając rozkład zmiennej losowej Y=X
2
należy najpierw wektor x podzielić, a
wektor krzywej rozkładu pomnożyć przez 4, a następnie metodami takimi, jak
dla integratora liniowego znaleźć rozkład sumy zmiennych losowych.
Znając rozkłady dla różnych wartości S/N można za pomocą funkcji
detect
stworzyć charakterystyki wykrywania. Na kolejnych wykresach 4.9a,b
znajdują się charakterystyki detekcji dla integratora liniowego i kwadratowego,
oraz dla porównania dla najlepszego integratora binarnego. Uzyskano je za
pomocą wyżej omówionych funkcji. Dalej w tabeli 4.3 zestawiono zysk dla
integratorów w stosunku do detekcji pojedynczego impulsu, dla D=0,9.
Tab. 4.3. Zysk w dB z zastosowania różnych typów integratorów dla D=0,9 i różnych M w
stosunku do pojedynczego impulsu
Zysk w dB, D=0,9
Typ
INT.
N
M
F=10
-6
F=10
-4
Lin
5
−
2.929
2.812
Lin
10
−
4.035
3.875
Sqr
5
−
2.840
2.725
Sqr
10
−
3.952
3.800
Bin
5
3
2.273
2.213
Bin
10
6
3.390
−
Bin
10
5
−
3.261
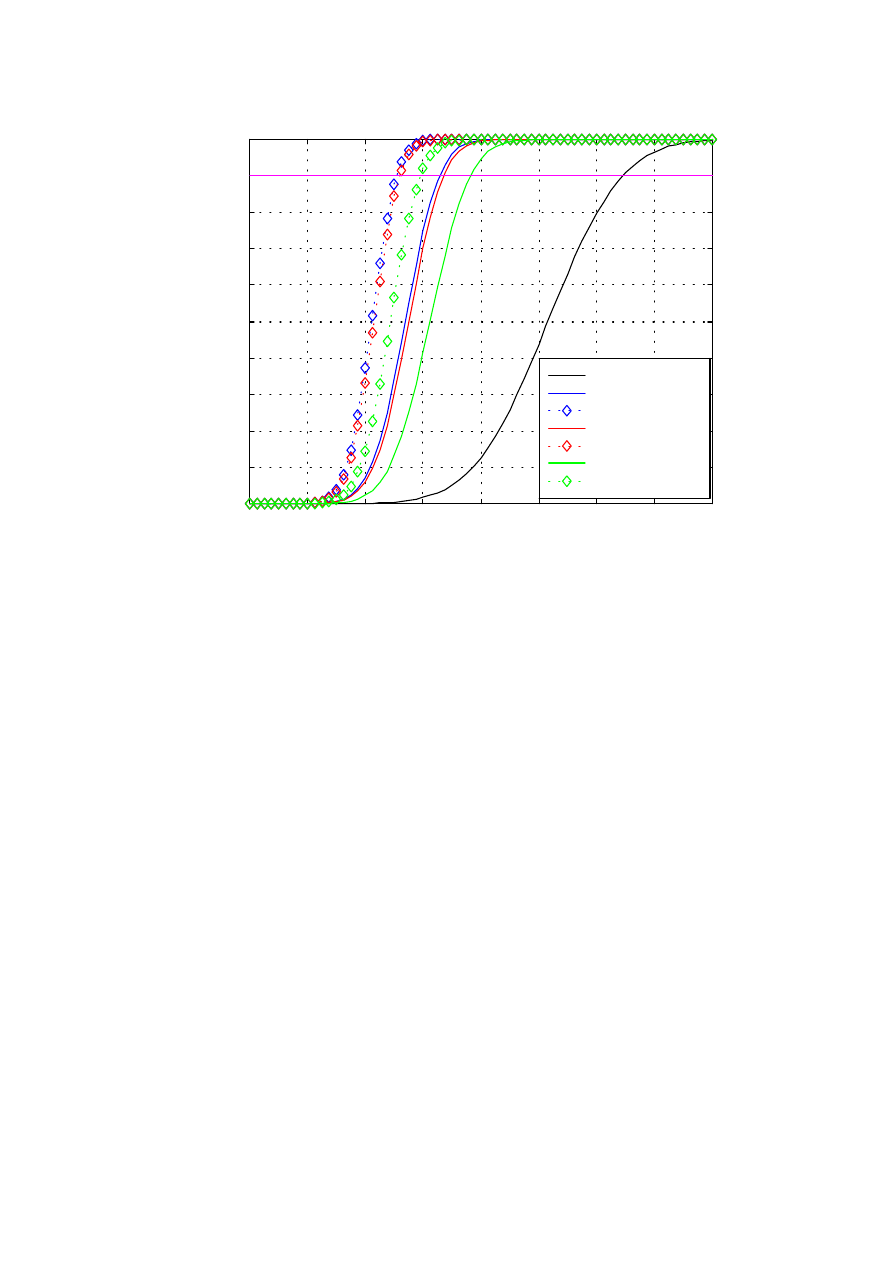
95
0
1
2
3
4
5
6
7
8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-6
N=1, M=1
lin: N=5
lin: N=10
sqr: N=5
sqr: N=10
bin: N=5, M=3
bin: N=10, M=6
Rys. 4.9a. Charakterystyki detekcji dla różnych integratorów dla F=10
-6.
Krzywa N=1,M=1 jest
charakterystyką dla pojedynczego impulsu. Wartości S/N są dla pojedynczego impulsu
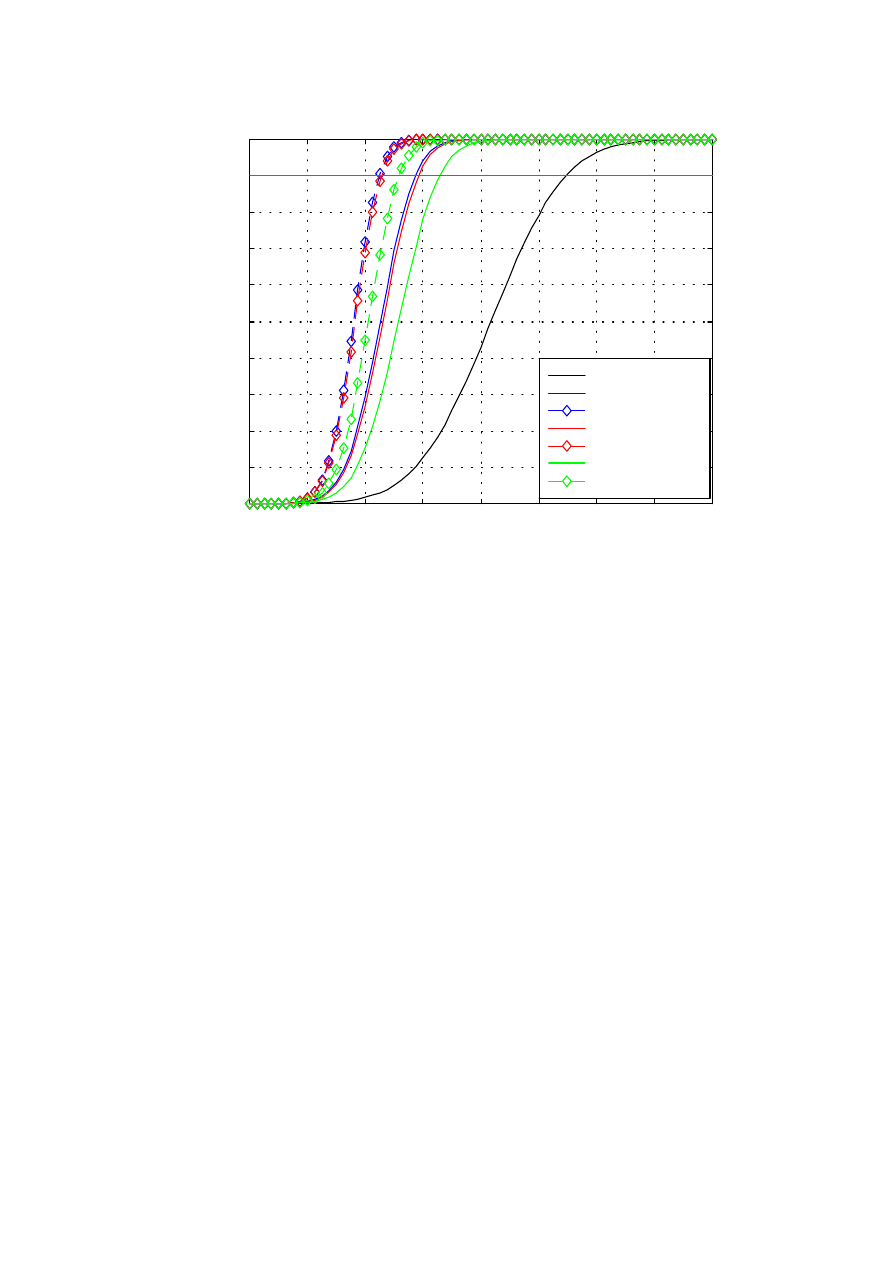
96
0
1
2
3
4
5
6
7
8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
F=1e-4
S/N
D
N=1, M=1
lin: N=5
lin: N=10
sqr: N=5
sqr: N=10
bin: N=5, M=3
bin: N=10, M=6
Rys. 4.9b. Charakterystyki detekcji dla różnych integratorów dla F=10
-4.
Krzywa N=1,M=1 jest
charakterystyką dla pojedynczego impulsu. Wartości S/N są dla pojedynczego impulsu
W rozdziale trzecim (punkt 3.3) wspomniano, iż w krańcowej sytuacji, gdy
poziomy sygnałów (impulsów) są bardzo małe w porównaniu z zakłóceniami,
detektor kwadratowy będzie lepszy od liniowego. Tak przynajmniej wynika z
kształtu krzywej
)
(
ln
0
u
I
. Jak widać na przedstawionych wykresach 4.9a i 4.9b
integrator liniowy nie jest gorszy od kwadratowego. Jest nawet w pokazanych
przypadkach w niewielkim stopniu lepszy. To, jaki typ integratora korzystniej
zastosować zależy od energii pojedynczego impulsu w stosunku do mocy
szumu, żądanego poziomu prawdopodobieństwa fałszywego alarmu czy liczby
integrowanych impulsów. Generalnie dla małych prawdopodobieństw
fałszywego alarmu i dużych prawdopodobieństw detekcji poziom sygnału
progowego dla obu typów integratorów jest taki sam [5]. Na wykresie 4.10
pokazano skrajny przypadek, gdzie integrator kwadratowy jest nieco lepszy od
liniowego. Zysk jest tak minimalny, że jego stosowanie zamiast liniowego i
niepotrzebne komplikowanie układu nie ma sensu.
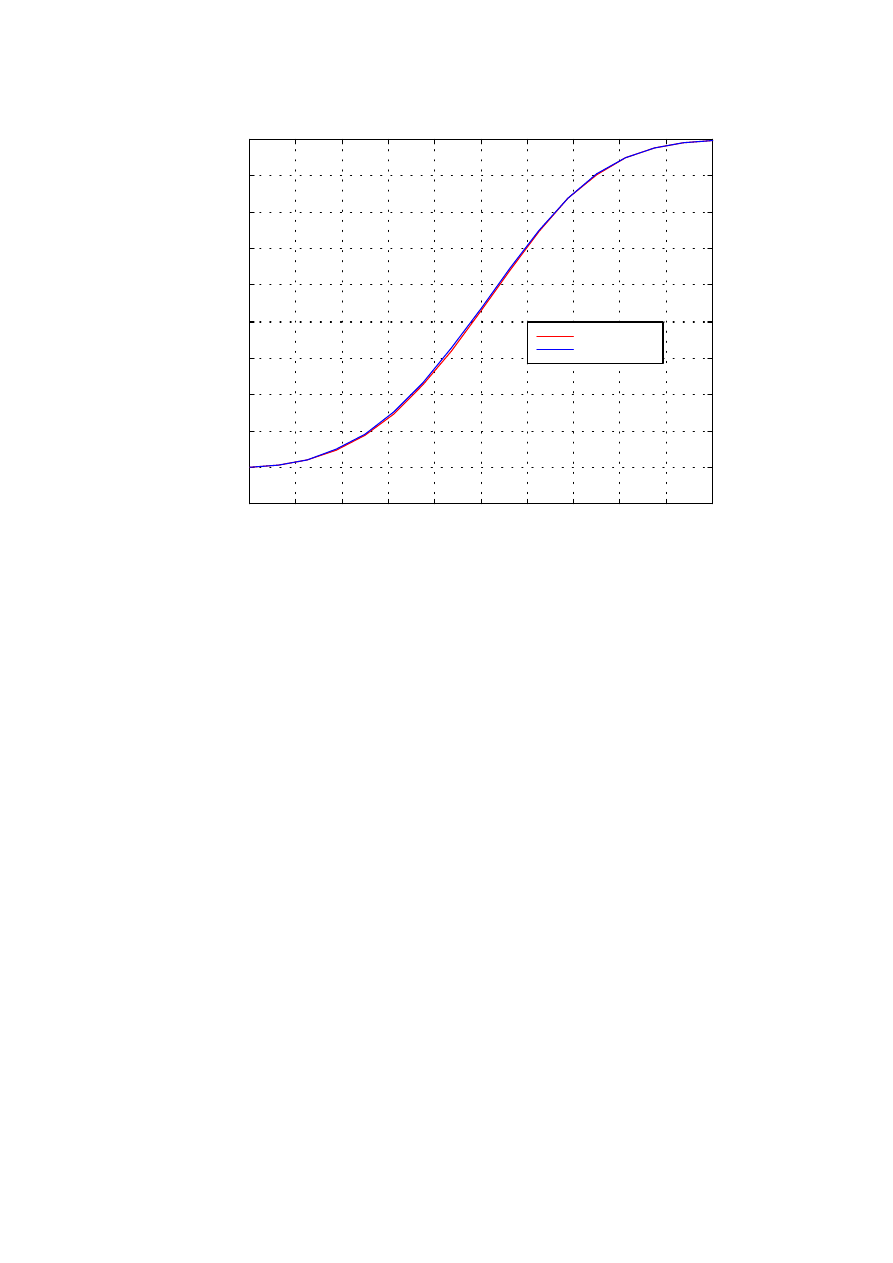
97
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
S/N
D
F=1e-1
lin: N=10
sqr: N=10
Rys. 4.10. Charakterystyki detekcji dla integratorów liniowego i kwadratowego dla F=10
-1
i N=10

98
PODSUMOWANIE
W pracy dokonano analizy statystycznej różnego rodzaju detektorów
cyfrowych, stosowanych we współczesnych systemach radarowych.
Przedstawiono podstawy teoretyczne procesu optymalnej detekcji oraz
rozważania prowadzące od teoretycznego optymalnego detektora do jak
najbliższych mu praktycznych realizacji. Dla rzeczywistych rozwiązań opisano
metody pozwalające określić rozkłady prawdopodobieństw sygnałów w
przypadkach odbierania jedynie zakłóceń oraz gdy odbiera się sumę zakłóceń i
sygnału użytecznego.
W oparciu o te metody napisano zestaw funkcji pracujących w środowisku
MATLAB, pozwalających na numeryczne wyznaczenie rozkładów
prawdopodobieństw, a także na wykreślenie na ich podstawie charakterystyk
detekcji dla różnych typów detektorów. Zdecydowano się na to środowisko z
uwagi na jego uniwersalność, a przede wszystkim na łatwość implementacji
różnorodnych algorytmów obliczeń numerycznych. MATLAB, jako środowisko i
język programowania wysokiego poziomu, idealnie nadaje się do tego typu
zadań obliczeniowych. Co najważniejsze, środowisko to jest otwarte i pozwala
na integrację własnych procedur z już istniejącymi.
W dodatkach A i B znajdują się opis stworzonych funkcji, służących do
analizy detektorów cyfrowych oraz wydruk ich kodu źródłowego. Z ich
wykorzystaniem dokonano przedstawionej w rozdziale czwartym analizy
wybranych detektorów w przypadku, gdy zakłócenia mają postać szumu białego
o rozkładzie Gauss’a oraz dzięki możliwościom graficznym MATLABA
zobrazowano wyniki na wykresach.
Uzyskane wykresy i wyniki świadczą o przydatności opracowanego
zestawu oprogramowania do analizy detektorów cyfrowych. Napisane funkcje

99
pracujące w środowisku MATLAB mogą służyć jako baza przy tworzeniu
bardziej rozbudowanych i wyspecjalizowanych aplikacji.

100
DODATEK A:
OPIS ZESTAWU FUNKCJI SŁUŻĄCYCH DO
ANALIZY DETEKTORÓW CYFROWYCH
Niniejszy dodatek stanowi dokumnetację zestawu funkcji służących do analizy detektorów
cyfrowych. Funkcje te zostały napisane i przetestowane w środowisku MATLAB w wersji 5.2. Niektóre z
nich wewnątrz siebie wywołują zarówno inne funkcje z pakietu, jak i te należące do standardowej
dystrybucji MATLAB’a. Z tego powodu istnieje możliwość, że w starszych wersjach środowiska
zadziałają niepoprawnie. W skład pakietu wchodzą następujące funkcje:
binint
wylicza charakterystyki detekcji dla integratora binarnego
dbloss
liczy różnicę w decybelach między dwoma charakterystykami detekcji dla określonego
poziomu prawdopodobieństwa detekcji
detect
wylicza charakterystyki detekcji dla pojedynczego impulsu
normaliz
wylicza rozkład prawdopodobieństwa zmiennej losowej Z=X/Y
pdftocdf
wylicza dystrybuantę zmiennej losowej P(x) lub krzywą 1-P(x)
ricepdf
wylicza krzywą rozkładu prawdopodobieństwa Rice’a
sqrtpdf
wylicza rozkład prawdopodobieństwa zmiennej losowej
2
2
Y
X
Z
+
=
sumpdf
generuje rozkład prawdopodobieństwa zmiennej losowej będącej
sumą N niezależnych zmiennych losowych o takich samych
rozkładach.
Na kolejnych stronach znajdują się dokładne opisy wyżej wymienionych funkcji,
natomiast dodatek B zawiera ich kod źródłowy.
binint
SKŁADNIA:
[d, sn]=binint(x, p, N, M, pfalse, snmax)
OPIS:
Funkcja generuje charakterystyki detekcji dla układu integratora binarnego (zwanego też dwuprogowym
lub M z N) przy zadanym poziomie prawdopodobieństwa fałszywego alarmu. Na podstawie rozkładów
prawdopodobieństw sygnału dla różnych wartości stosunków SYGNAŁ/SZUM
)
( E
x
p
gdzie E jest energią sygnału użytecznego najpierw oblicza “odwrotną”
dystrybuantę
)
(
1
E
x
P
−

101
czyli prawdopodobieństwo, że sygnał przekroczy pewien poziom x. Robi to wywoływana wewnątrz
binint
funkcja
pdftocdf
(jej opis znajduje się kilka stron dalej). Następnie zgodnie ze wzorem na
schemat Bernouliego liczy prawdopodobieństwo, że M i więcej impulsów z N w paczce przekroczy
poziom x. Z tak uzyskanych danych dla zadanego poziomu prawdopodobieństwa fałszywego alarmu F
wyliczane są krzywe detekcji. Ponieważ rozkłady prawdopdobieństw mają postać dyskretną (zarówno
zmienna losowa X, jak i odpowiadające jej wartości prawdopodobieństw zmieniają się w sposób
skokowy), to aby określić prawdopodobieństwo dla x
0
o wartości z pomiędzy danych x-ów tzn.
2
0
1
0
:
x
x
x
x
<
<
zastosowano metodę aproksymacji liniowej.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X (inaczej wektor wartości,
jakie może przyjmować sygnał i szum w pojedynczym impulsie)
p
−
macierz, w której każda kolumna jest rozkładem
prawdopodobieństwa zmiennej losowej X dla pojedynczego
impulsu, przy czym kolumna pierwsza jest rozkładem tylko dla
szumu, zaś kolejne kolumny rozkładami sumy sygnał+szum dla
różnych coraz większych wartości stosunku SYGNAŁ/SZUM
N
,
M
−
parametry integratora
pfalse
−
ustalone dopuszczalne prawdopodobieństwo fałszywego
alarmu
snmax
−
wartość maksymalnego stosunku SYGNAŁ/SZUM (dla rozkładu
z ostatniej kolumny macierzy
p
)
WYJŚCIE:
sn
−
wektor kolumnowy stosunku SYGNAŁ/SZUM (wektor
równomiernie rozłożonych wartości od zera do
snmax
d
−
wektor kolumnowy prawdopodobieństw detekcji
PRZYKŁAD:
Poniższa sekwencja wyliczy charakterystykę detekcji dla integratora binarnego
typu 5 z 10 przy założeniu, że pojedynczy impuls ma rozkład Rice’a,
maksymalny stosunek SYGNAŁ/SZUM wynosi 20, a prawdopodobieństwo
fałszywego alarmu F=10
-6
. Funkcja
ricepdf
nie jest częścią Matlaba. Jej opis
znajduje się kilka stron dalej.
E=[0:0.5:20]’; x=[0:0.1:40]’;
for i=1:length(E)
p(:,i)=ricepdf(x, 1, E(i));
end
[d sn]=binint(x, p, 10, 5, 1e-6, 20);

102
dbloss
SKŁADNIA:
d=dbloss(x1, f1x, x2, f2x, l)
OPIS:
Funkcja liczy różnicę w decybelach między dwoma charakterystykami detekcji dla określonego poziomu
prawdopodobieństwa detekcji tzn. różnicę między stosunkami SYGNAŁ/SZUM, dla których obie krzywe
mają taką samą wielkość prawdopodobieństwa detekcji. Funkcja także działa dobrze dla wszystkich
krzywych niemalejących. Jeśli po wywołaniu funkcji pojawi się komunikat o błędzie i niezdefiniowaniu
zmiennych
i1
lub
i2
, oznacza to, że któryś z przebiegów dla zadanego poziomu
l
nie ma określonej
wartości.
PARAMETRY WEJŚCIOWE:
x1
−
wektor kolumnowy dziedziny (wartości stosunków
SYGNAŁ/SZUM) pierwszej krzywej
fx1
−
wektor kolumnowy zbioru wartości (prawdopodobieństw
detekcji) pierwszej krzywej
x2
,
fx2
−
wektory kolumnowe dziedziny i zbioru wartości drugiej krzywej
l
−
wartość, dla której liczona jest różnica stosunków
SYGNAŁ/SZUM
WYJŚCIE:
d
−
różnica w dB między stosunkami SYGNAŁ/SZUM, dla których
obie krzywe mają taką samą wartość prawdopodobieństwa
detekcji
PRZYKŁAD:
Liczona jest różnica dla dwóch różnych wartości
l
:
x1=[1 2 3 4 5]';
fx1=[1 2 3 4 5]';
x2=[6 7 8 9 10]';
fx2=[1 3 3 7 10]';
dbloss(x1,fx1,x2,fx2,3)
% ans = 3.67976785294594
dbloss(x1,fx1,x2,fx2,6)
% błąd, bo dla l=6 fx1 nie ma
określonej wartości

103
detect
SKŁADNIA:
[d, sn]=detect(x, p, pfalse, snmax)
OPIS:
Funkcja generuje charakterystyki detekcji dla pojedynczego impulsu przy zadanym poziomie
prawdopodobieństwa fałszywego alarmu. Na podstawie rozkładów prawdopodobieństw sygnału dla
różnych wartości stosunków SYGNAŁ/SZUM
)
( E
x
p
gdzie E jest energią sygnału użytecznego, oblicza najpierw “odwrotną”
dystrybuantę
)
(
1
E
x
P
−
czyli prawdopodobieństwo, że sygnał przekroczy pewien poziom x. Robi to wywoływana wewnątrz
detect
funkcja
pdftocdf
(jej opis znajduje się kilka stron dalej). Z tak uzyskanych danych dla
zadanego poziomu prawdopodobieństwa fałszywego alarmu F wyliczane są krzywe detekcji. Ponieważ
rozkłady prawdopdobieństw mają postać dyskretną (zarówno zmienna losowa X, jak i odpowiadające jej
wartości prawdopodobieństw zmieniają się w sposób skokowy), to aby określić prawdopodobieństwo dla
x
0
o wartości z pomiędzy danych x-ów tzn.
2
0
1
0
:
x
x
x
x
<
<
zastosowano metodę aproksymacji liniowej.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X (inaczej wektor wartości,
jakie może przyjmować sygnał i szum w pojedynczym impulsie)
p
−
macierz, w której każda kolumna jest rozkładem
prawdopodobieństwa zmiennej losowej X dla pojedynczego
impulsu, przy czym kolumna pierwsza jest rozkładem tylko dla
szumu, zaś kolejne kolumny rozkładami sumy sygnał+szum dla
różnych coraz większych wartości stosunku SYGNAŁ/SZUM
pfalse
−
ustalone dopuszczalne prawdopodobieństwo fałszywego
alarmu
snmax
−
wartość maksymalnego stosunku SYGNAŁ/SZUM (dla rozkładu
z ostatniej kolumny macierzy
p
)
WYJŚCIE:
sn
−
wektor kolumnowy stosunku SYGNAŁ/SZUM (wektor
równomiernie rozłożonych wartości od zera do
snmax
d
−
wektor kolumnowy prawdopodobieństw detekcji
PRZYKŁAD:

104
Poniższa sekwencja wyliczy charakterystykę detekcji dla opisanego w rozdziale
pierwszym przypadku miernika wychyłowego, gdzie mierzona wielkość zmienia
się od zera do 5, błąd pomiaru ma rozkład Gaussa o
σ
=0,2, F=10
-4
:
X=[0:0.5:5]’;
y=[-10:0.1:10]’;
for i=1:length(X)
p(:,i)=normpdf(x, X(i), 0.2);
end
[d sn]=detect(x, p, 1e-4, 5);

105
normaliz
SKŁADNIA:
[p]=normaliz(x, m, 'fun', varargin)
OPIS:
Funkcja generuje rozkład prawdopodobieństwa zmiennej losowej Z:
Y
X
Z
=
gdzie X jest zmienną losową, której rozkład tworzony jest na bazie argumentu
x
przez dowolną funkcję oznaczoną w składni jako
fun
, zaś wartości
prawdopodobieństw rozkładu zmiennej Y zawiera wektor
m.
Wektor
m
może
mieć inną długość niż
x
, ale przyjmuje się, że zmienna Y tak jak i X należy do
przedziełu
max
min
; x
x
.
Funkcja określona jako
fun
musi być tak napisana, aby jej pierwszym
argumentem był wektor
x
. Szczegóły na temat metody zastosowanej do
generacji rozkładu zmiennej Z można znaleźć w rozdziale czwartym.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X
m
−
wektor kolumnowy rozkładu zmiennej losowej Y
'
fun
'
−
nazwa funkcji generującej rozkład zmiennej X
varargin
−
zamiast tego napisu należy podać wszystkie pozostałe
argumenty (oddzielone przecinkami) dla funkcji
fun
WYJŚCIE:
p
−
wektor kolumnowy opisujący rozkład zmiennej losowej Z
PRZYKŁAD:
Sekwencja na następnej stronie wyliczy rozkłady prawdopodobieństwa sygnału
za układem CFAR dla N=16. Moc sygnału zmienia się od zera do 20.
x=linspace(0,40,1024)';
m=sumpdf(linspace(0,40,8192)',
raylpdf(linspace(0,40,8192)',1),16);
for A=0:0.25:20
n(:,A)=normaliz(x, m,'ricepdf', 1, A);

106
end

107
pdftocdf
SKŁADNIA:
[c]=pdftocdf(x, p, 'fwd')
[c]=pdftocdf(x, p, 'inv') lub [c]=pdftocdf(x, p)
OPIS:
Funkcja na podstawie rozkładu prawdopodobieństwa generuje dystrybuantę
zmiennej losowej X:
)
(x
P
lub krzywą
)
(
1
x
P
−
określającą prawdopodobieństwo, że zmienna losowa będzie większa od
wartości x. Z uwagi na to, że zarówno zmienna losowa x, jak i odpowiadające
jej wartości prawdopodobieństw zmieniają się w sposób skokowy dystrybuanta
liczona jest nie poprzez całkowanie (np. metodą trapezów) ale jako suma
kumulatywna wartości wektora p(x) pomnożona przez krok, co jaki zmieniają się
wartości wektora
x
. Sumę kumulatywną liczy bardzo szybka wbudowana
funkcja MATLAB’a
cumsum
. W celu szybkiego wyliczenia krzywej 1-P(x)
zastosowano przed i po wywołaniu
cumsum
funkcję
flipud
odwracającą
kolejność danych w wektorze.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X
p
−
wektor kolumnowy funkcji gęstości prawdopodobieństwa p(x).
Jeśli argument
p
jest macierzą, to jej kolumny są traktowane
jako rozkłady warunkowe tej samej zmiennej losowej X
‘
fwd
’
−
liczona jest dystrybuanta zmiennej losowej X: P(x)
‘
inv
’
−
liczona jest "odwrotna" dystrybuanta tzn. 1-P(x). Niepodanie
parametru jest równoważne podaniu '
inv
'
WYJŚCIE:

108
c
−
"prosta" lub "odwrotna" dystrybuanta zmiennej X (wektor
kolumnowy lub macierz, jeśli argument wejściowy
p
jest
macierzą)
PRZYKŁAD:
Poniższa sekwencja wyliczy i wykreśli dystrybuantę standardowego rozkładu
normalnego:
x=[0:0.5:5]’;
p=normpdf(x, 0, 1);
c=pdftocdf(x, p,
'
fwd
'
);

109
ricepdf
SKŁADNIA:
[p]=ricepdf(x, sigma, A)
OPIS:
Funkcja generuje rozkład prawdopodobieństwa Rice’a o parametrach
σ
oraz A zgodnie z poniższym wzorem:
0
),
(
)
2
exp(
)
(
2
0
2
2
2
2
>
⋅
+
−
=
x
xA
I
A
x
x
x
p
σ
σ
σ
gdzie
0
I
jest zmodyfikowaną funkcją Bessela pierwszego rodzaju zerowego rzędu. W funkcji zmieniono
odpowiednio kolejność obliczeń tak, aby dla dużych x-ów nie dochodziło do liczenia iloczynu
"
0
"
∞
⋅
W
przypadku, gdy A=0 wzór znacznie się upraszcza:
0
),
2
exp(
)
(
2
2
2
>
−
=
x
x
x
x
p
σ
σ
Opisuje on funkcję gęstości prawdopodobieństwa Rayleya.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X
sigma
,
A
−
parametry rozkładu:
σ
, A
WYJŚCIE:
p
−
wektor kolumnowy opisujący rozkład zmiennej losowej X
PRZYKŁAD:
Następująca sekwencja wygeneruje i wykreśli rozkład Rice’a o parametrach
σ
=1 oraz A=5:
x=[0:0.01:10]’;
p=ricepdf(x, 1, 5);
plot(x,p);

110
sqrtpdf
SKŁADNIA:
[p]=sqrtpdf(x, 'fun1', 'fun2', varargin)
[p]=sqrtpdf(x, '', '', mu1, mu2, sigma1, sigma2)
OPIS:
Funkcja generuje rozkład prawdopodobieństwa zmiennej losowej Z:
2
2
Y
X
Z
+
=
gdzie X jest zmienną losową, której rozkład tworzony jest na bazie argumentu
x
przez dowolną funkcję oznaczoną w składni jako
fun1
, zaś Y analogicznie
przez funkcję oznaczoną w składni jako
fun2
. Obie funkcje muszą być tak
napisane, aby ich pierwszym argumentem był wektor
x
. W przypadku
niepodania nazw funkcji (drugi sposób wywołania) zmienne X i Y będą miały
rozkład Gaussa o parametrach:
X:
µ
X
=
mu1
,
σ
X
=
sigma1
Y:
µ
Y
=
mu2
,
σ
Y
=
sigma2
Szczegóły na temat metody zastosowanej do generacji rozkładu zmiennej Z
można znaleźć w rozdziale czwartym.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X i Y
'
fun1
'
−
dowolna nazwa istniejącej funkcji generującej rozkład zmiennej
X
'
fun2
'
−
jak wyżej dla rozkładu zmiennej Y
varargin
−
zamiast tego napisu należy podać wszystkie pozostałe
argumenty (oddzielone przecinkami) dla funkcji
fun1
i
fun2
kolejno: arg1_fun1, arg1_fun2, arg2_fun1, arg2_fun2, ...
WYJŚCIE:
p
−
wektor kolumnowy wartości prawdopodobieństw dla rozkładu
zmiennej losowej Z (wartości zmiennej Z opisuje wektor
x
)
PRZYKŁAD:
Poniższa sekwencja wyliczy i wykreśli rozkład Rice’a o parametrach
σ
=1 oraz A=5. Jest równoważna
przykładowi podanemu dla funkcji
ricepdf
.
x=[0:0.01:10]’;

111
p=sqrtpdf(x, 'normpdf', 'normpdf', 0, 5, 1, 1);
plot(x,p);

112
sumpdf
SKŁADNIA:
[py y]=sumpdf(x, px, N, 'mean') lub [py y]=sumpdf(x, px, N)
[py y]=sumpdf(x, px, N, 'sum')
OPIS:
Funkcja generuje rozkład prawdopodobieństwa zmiennej losowej będącej sumą N
niezależnych zmiennych losowych X o takich samych rozkładach. W zależności od
tego, jaki podano czwarty argument funkcji, generuje ona rozkład średniej
opisany poniższym wzorem
∑
=
=
N
i
X
N
Y
1
1
−
gdy podano
'mean'
lub rozkład sumy zmiennych X:
∑
=
=
N
i
X
Y
1
−
dla czwartego argumentu
'sum'
W celu przyspieszenia obliczeń zamiast N-razy liczyć splot zastosowano
przejście przez funkcję charakterystyczną, która równa jest transformacie
Fouriera z rozkładu prawdopodobieństwa. Funkcja
sumpdf
najpierw za
pomocą metody FFT liczy dyskretną transformatę Fouriera o ilości
punktów
N
razy długość wektora
x
, następnie podnosi do N-tej potęgi i
liczy odwrotną DTF. W zależności od tego, czy liczony jest rozkład
średniej, czy sumy wykonywane jest odpowiednie skalowanie wyników
przez
N
.
PARAMETRY WEJŚCIOWE:
x
−
wektor kolumnowy zmiennej losowej X
px
−
wektor kolumnowy funkcji gęstości prawdopodobieństwa p(x)
N
−
liczba sumowanych zmiennych losowych
‘
mean
’
−
funkcja wygeneruje rozkład średniej
‘
sum
’
−
funkcja wygeneruje rozkład sumy. Parametr ten jest opcjonalny.
Niepodanie go jest równoważne podaniu '
mean
'
WYJŚCIE:
py
−
wektor kolumnowy opisujący rozkład zmiennej losowej Y
y
−
wektor kolumnowy zmiennej losowej Y

113
PRZYKŁAD:
Następująca sekwencja wygeneruje rozkład estymatora wartości średniej dla N=10 pomiarów, gdzie
mierzona wartość przyjmuje wartości od zera do 10:
x=[0:0.01:10]’;
px=ones(length(x),1).*0.1
[py y]=sumpdf(x, px, 10,
'
mean
'
);
plot(x,px, y, py);

114
DODATEK B:
KODY ŹRÓDŁOWE FUNKCJI SŁUŻĄCYCH DO
ANALIZY DETEKTORÓW CYFROWYCH
binint.m
function [d, sn]=binint(x, p, N, M, pfalse, snmax)
%
%[d, sn]=binint(x, p, N, M, pfalse, snmax)
%
% Generuje charakterystyke detekcji, czyli wykres prawdopodobienstwa
% detekcji od stosunku SYGNAL/SZUM dla ukladu integratora binarnego
% (integratora typu M z N), przy zadanym poziomie prawdopodobienstwa
% falszywego alarmu
%
% PARAMETRY WEJSCIOWE:
% x - zmienna losowa X (wektor kolumnowy), czyli wektor
% wartosci, jakie moze przyjmowac sygnal i szum w
% pojedynczym impulsie
% p - macierz, w ktorej kazda kolumna jest rozkladem
% prawdopodobienstwa zmiennej losowej X dla pojedynczego
% impulsu, przy czym kolumna pierwsza jest rozkladem
% tylko dla szumu, zas kolejne kolumny rozkladami
% sumy sygnal+szum dla roznych coraz wiekszych wartosci
% stosunku SYGNAL/SZUM
% N, M - parametry integratora binarnego (M z N)
% pfalse - ustalone dopuszczalne prawdopodobienstwo falszywego
% alarmu
% snmax - warotsc maksymalnego stosunku SYGNAL/SZUM (dla
% rozkladu z ostatniej kolumny macierzy 'p')
% WYJSCIE:
% sn - wektor kolumnowy stosunku SYGNAL/SZUM (wektor
% rownomiernie rozlozonych wartosci od zera do 'snmax'
% d - wektor kolumnowy prawdopodobienst detekcji
%
% Sprawdzone w srodowisku MATLAB 5.x
%
%tic
if (N<0 | M<0 | M>N)
display('Blad danych wejsciowych');
return;
end
p=pdftocdf(x, p);
siz=size(p);

115
for i=1:siz(1)
for j=1:siz(2)
p_out=0;
%p_out=sum(binopdf([M:1:N]', N, p(i,j)));
for k=M:N
p_out=p_out+(nchoosek(N,k).*(p(i,j).^k).*((1-p(i,j)).^(N-
k)));
end
p(i,j)=p_out;
%i
end
end
for i=1:siz(1)-1
if p(i,1)>pfalse & p(i+1,1)<pfalse
i1=i;
i2=i+1;
break;
end
end
a=(p(i2,1)-p(i1,1))./(i2-i1);
b=p(i1,1)-a.*i1;
x=(pfalse-b)./a;
d(1,1)=pfalse;
for i=2:siz(2)
a=(p(i2,i)-p(i1,i))./(i2-i1);
b=p(i1,i)-a.*i1;
d(i,1)=a.*x+b;
end
sn=linspace(0,snmax,siz(2))';
%toc
dbloss.m
function d=dbloss(x1, f1x, x2, f2x, l)
%
%d=dbloss(x1, f1x, x2, f2x, l)
%
% Funkcja liczy roznice w decybelach miedzy dwoma charakterystykami
% detekcji dla okreslonego poziomu prawdopodobienstwa detekcji tzn.
% roznice miedzy stosunkami SYGNAL/SZUM, dla ktorych obie krzywe
% maja taka sama wielkosc prawdopodobienstwa detekcji.
%
% PARAMETRY WEJSCIOWE:
% x1 - wektor kolumnowy dziedziny (wartosci stosunkow
% SYGNAL/SZUM) pierwszej krzywej
% f1x - wektor kolumnowy zbioru wartosci (prawdopodobienstw
% detekcji) pierwszej krzywej
% x2, f2x - wektory kolumnowe dziedziny i zbioru wartosci drugiej
% krzywej
% l - wartosc, dla ktorej liczona jest roznica stosunkow
% SYGNAL/SZUM
% WYJSCIE:
% d - roznica w dB miedzy stosunkami SYGNAL/SZUM, dla
% ktorych obie krzywe maja taka sama wartosc
% prawdopodobienstwa detekcji
%
% Jesli funkcja wyswietli
blad, że zmienna 'i1' lub 'i2' jest

116
% niezdefiniowana, to oznacza, ze ktorys z przebiegow
% dla zadanego poziomu 'l' nie ma okreslonej wartosci
%
% Sprawdzone w srodowisku MATLAB 5.x
%
len=length(f1x);
for i=1:len-1
if f1x(i,1)<l & f1x(i+1,1)>=l
i1=i;
i2=i+1;
break;
end
end
a=(f1x(i2,1)-f1x(i1,1))./(i2-i1);
b=f1x(i2,1)-a.*i2;
xx=(l-b)./a;
a=(x1(i2,1)-x1(i1,1))./(i2-i1);
b=x1(i1,1)-a.*i1;
d1=a.*xx+b;
len=length(f2x);
for i=1:len-1
if f2x(i,1)<l & f2x(i+1,1)>=l
i1=i;
i2=i+1;
break;
end
end
a=(f2x(i2,1)-f2x(i1,1))./(i2-i1);
b=f2x(i2,1)-a.*i2;
xx=(l-b)./a;
a=(x2(i2,1)-x2(i1,1))./(i2-i1);
b=x2(i1,1)-a.*i1;
d2=a.*xx+b;
d1, d2
d=abs(10*log10(d2)-10*log10(d1));
detect.m
function [d, sn]=detect(x, p, pfalse, snmax)
%
%[d, sn]=detect(x, p, pfalse, snmax)
%
% Generuje charakterystyke detekcji, czyli wykres prawdopodobienstwa
% detekcji od stosunku SYGNAL/SZUM dla sygnalu ukrytego w szumie,przy
% zadanym poziomie prawdopodobienstwa falszywego alarmu
%
% PARAMETRY WEJSCIOWE:
% x - zmienna losowa X (wektor kolumnowy), czyli wektor
% wartosci, jakie moze przyjmowac sygnal i szum
% p - macierz, w ktorej kazda kolumna jest rozkladem
% prawdopodobienstwa zmiennej losowej X, przy czym
% kolumna pierwsza jest rozkladem tylko dla szumu, zas
% kolejne kolumny rozkladami sumy sygnal+szum dla
% roznych coraz wiekszych wartosci stosunku SYGNAL/SZUM
% pfalse - ustalone dopuszczalne prawdopodobienstwo falszywego
% alarmu
% snmax - warotsc maksymalnego stosunku SYGNAL/SZUM (dla
% rozkladu z ostatniej kolumny macierzy 'p')

117
% WYJSCIE:
% sn - wektor kolumnowy stosunku SYGNAL/SZUM (wektor
% rownomiernie rozlozonych wartosci od zera do 'snmax'
% d - wektor kolumnowy prawdopodobienst detekcji
%
% Sprawdzone w srodowisku MATLAB 5.x
%
tic
p=pdftocdf(x, p);
siz=size(p);
for i=1:siz(1)-1
if p(i,1)>pfalse & p(i+1,1)<pfalse
i1=i;
i2=i+1;
break;
end
end
a=(p(i2,1)-p(i1,1))./(i2-i1);
b=p(i1,1)-a.*i1;
xx=(pfalse-b)./a;
d(1,1)=pfalse;
for i=2:siz(2)
a=(p(i2,i)-p(i1,i))./(i2-i1);
b=p(i1,i)-a.*i1;
d(i,1)=a.*xx+b;
end
sn=linspace(0,snmax,siz(2))';
toc
normaliz.m
function [p]=normaliz(x, m, fun, varargin)
%
%[p]=normaliz(x, m, 'fun', varargin)
%
% Generuje funkcje gestosci prawdopodobienstwa zmiennej losowej
% Z = X ./ Y, gdzie:
% X: zmienna losowa, ktorej rozklad tworzy na bazie parametru
% wejsciowego 'x' wywolywana wewnatrz funkcja, ktorej nazwe
% przekazuje sie przez argument 'fun'
% (X nalezy do przedzialu <xmin..xmax>)
% Y: zmienna losowa o rozkladzie opisanym wektorem 'm'
% (Y jak i X takze nalezy do przedzialu <xmin..xmax>, ale wektor
% 'm' moze miec inna dlugosc niz 'x')
% Zastosowano metode przejscia przez rozklad dwuwymiarowy tzn.
% /
% f(z)=|f(x,y)dy, zas
% /
% f(x,y)=f(x1*y1,y1)*|y1|=f(x1*y1)*f(y1)*|y1|,
% jesli zmienne sa niezalezne. Szczegoly w ksiazce A. Pacuta
% "Prawdopodobienstwo, teoria, modelowanie
% probabilistyczne w technice".
%
% PARAMETRY WEJSCIOWE:
% x - wektor kolumnowy zmiennej losowej X
% m - wektor kolumnowy rozkladu zmiennej losowej Y

118
% fun - nazwa funkcji generujacej rozklad zmiennej X
% varargin - dodatkowe argumenty funcji 'fun'
% (pierwszym parametrem, ktorego sie tu nie podaje jest
% zawsze 'x')
% WYJSCIE:
% p - wektor kolumnowy opisujacy rozklad zmiennej losowej Z
%
% Sprawdzone w srodowisku MATLAB 5.x
%
X=linspace(x(1),x(length(x)),length(m))';
MX=m.*X;
Z=zeros(length(m),1);
p=zeros(length(x),1);
%tic
for i=1:length(x)
Z=feval(fun, x(i,1).*X, varargin{:});
Z=Z.*MX;
p(i,1)=trapz(X,Z);
%i
end
%toc
pdftocdf.m
function [c]=pdftocdf(x, p, todo)
%
%[c]=pdftocdf(x, p, 'fwd')
%[c]=pdftocdf(x, p, 'inv') lub [c]=pdftocdf(x, p)
%
% Generuje dystrybuante zmiennej losowej X: P(x) lub
% "odwrotna" dystrybuante tzn. 1-P(x)
%
% PARAMETRY WEJSCIOWE:
% x - wektor kolumnowy zmiennej losowej X
% p - wektor kolumnowy funkcji gestosci
% prawdopodobienstwa p(x).
% Jesli argument 'p' jest macierza, to jej kolumny sa
% traktowane jako rozklady warunkowe tej samej
% zmiennej losowej X
% 'fwd' - liczona jest dystrybuanta zmiennej losowej X: P(x)
% 'inv' - liczona jest "odwrotna" dystrybuanta tzn. 1-P(x).
% Niepodanie parametru jest rownowazne podaniu 'inv'
% WYJSCIE:
% c - "prosta" lub "odwrotna" dystrybuanta zmiennej X
% (wektor kolumnowy lub macierz, jesli argument
% wejsciowy 'p' jest macierza)
%
% Sprawdzone w srodowisku MATLAB 5.x
%
%tic
if exist('todo')==0 | isempty(todo)
todo='inv';
end
step=abs(x(2)-x(1));
if strcmp(todo, 'inv')

119
p=flipud(p);
c=cumsum(p).*step;
c=flipud(c);
else
c=cumsum(p).*step;
end
%toc
ricepdf.m
function [p]=ricepdf(x, sigma, A)
%
%[p]=ricepdf(x, sigma, A)
%
% Generuje funkcje gestosci prawdopodobienstwa Rice'a
% (lub Rayley'a, jesli A=0) zgodnie ze wzorem:
%
% p(x)=x/sigma^2 * exp(- x^2+A^2/2sigma^2) * I (xA/sigma^2)
% 0
% PARAMETRY WEJSCIOWE:
% x - wektor kolumnowy zmiennej losowej X
% sigma, A - parametry rozkladu
%
% WYJSCIE:
% p - wektor kolumnowy opisujacy rozklad zmiennej losowej X
%
% Sprawdzone w srodowisku MATLAB 5.x
%
%tic
%p=(x./(sigma.^2)).*exp(-
((x.^2)+(A.^2))./(2.*sigma.^2)).*besseli(0,(x.*A)./(sigma.^2));
p=(x./(sigma.^2)).*exp((-(x.^2)+2.*A.*x)./(2.*sigma.^2)).*exp(-
(A.^2)./(2.*sigma.^2));
p=p.*besseli(0,(x.*A)./(sigma.^2),1);
%for i=1:length(p)
% if isnan(p(i)) | isinf(p(i))
% p(i)=0;
% end
%end
%toc
sqrtpdf.m
function [p]=sqrtpdf(x, fun1, fun2, varargin)
%
%[p]=sqrtpdf(x, 'fun1', 'fun2', varargin)
%[p]=sqrtpdf(x, '', '', mu1, mu2, sigma1, sigma2)
%
% Generuje funkcje gestosci prawdopodobienstwa zmiennej losowej
% Z = sqrt( X.^2 + Y.^2 ), gdzie:
% X: zmienna losowa o rozkladzie tworzonym na bazie parametru 'x'
% przez funkcje 'fun1'
% Y: jak wyzej, rozklad tworzony przez 'fun2' na bazie
% parametru 'x'
% Zastosowano metode przejscia przez rozklad dwuwymiarowy tzn.
% /
% f(z)=|f(x,y)dy, zas
% /
% f(x,y)=f(x1*cos y1)*f(x1*sin y1)*|x1| jesli zmienne sa niezalezne.

120
% Skorzystano przy tym z przeksztalcenia g:R^2-->R^2 jak ponizej:
% z = sqrt(x.^2+y.^2) ---\ x = z*cos fi
% fi = arctan(y/x) ---/ y = z*sin fi
%
% PARAMETRY WEJSCIOWE:
% x - wektor kolumnowy zmiennej losowej X i Y
% fun1 - nazwa funkcji generujacej rozklad zmiennej X
% fun2 - nazwa funkcji generujacej rozklad zmiennej Y
% varargin - dodatkowe parametry dla 'fun1' i 'fun2'
% (kolejno arg1_fun1, arg1_fun2, arg2_fun1, ...)
% pierwszym parametrem 'fun1' i 'fun2' jest zawsze 'x'
% Jesli skorzysta sie z drugiej metody wywolania funkcji tzn. nie
% poda sie 'fun1' i 'fun2', wowczas zmienne losowe X i Y beda mialy
% rozklad Gaussa o parametrach kolejno mu1, sigma1 oraz mu2, sigma2
%
% WYJSCIE:
% p - wektor kolumnowy opisujacy rozklad zmiennej losowej Z
%
% Sprawdzone w srodowisku MATLAB 5.x
%
%tic
FILEN=256;
fi=linspace(0,2*pi,FILEN)';
Z=zeros(length(x),1);
p=zeros(length(x),1);
if isempty(fun1) | isempty(fun2)
for i=1:length(x)
Z=(exp(-0.5.*(varargin{3}.^(-2)).*((x(i,1).*cos(fi))-
varargin{1}).^2)./(sqrt(2*pi).*varargin{3})).*(exp(-
0.5.*(varargin{4}.^(-2)).*((x(i,1).*sin(fi))-
varargin{2}).^2)./(sqrt(2*pi).*varargin{4})).*abs(x(i,1));
p(i,1)=trapz(fi,Z);
end
else
for i=1:length(x)
Z=feval(fun1, x(i,1).*cos(fi),
varargin{1:2:length(varargin)}).*feval(fun2, x(i,1).*sin(fi),
varargin{2:2:length(varargin)}).*abs(x(i,1));
p(i,1)=trapz(fi,Z);
end
end
%toc
sumpdf.m
function [py, y]=sumpdf(x, px, N, todo)
%
%[py y]=sumpdf(x, px, N, 'mean') lub [py y]=sumpdf(x, px, N)
%[py y]=sumpdf(x, px, N, 'sum')
%
% Generuje funkcje gestosci prawdopodobienstwa zmiennej losowej
% bedacej suma N tych samych zmiennych losowych X:
% N
% Y = sum(X)
% i=1
%
% lub zmienna bedaca estymatorem wartosci sredniej tzn. jesli
% X - zmienna losowa wejsciowa, to

121
% N
% Y = 1/N * sum(X)
% i=1
%
% Zeby przyspieszyc obliczenia dla duzego N zastosowano przejscie
% przez funkcje tworzaca rozkladu
%
% PARAMETRY WEJSCIOWE:
% x - wektor kolumnowy zmiennej losowej X
% px - wektor kolumnowy funkcji gestosci
% prawdopodobienstwa p(x)
% N - patrz wzor na Y
% 'mean'
% 'sum' - okresla, czy funkcja wygeneruje rozklad sredniej
% ('mean'), czy sumy ('sum') zmiennych losowych.
% Parametr ten jest opcjonalny. Niepodanie go jest
% rownowazne podaniu 'mean'
% WYJSCIE:
% py - wektor kolumnowy opisujacy rozklad zmiennej losowej Y
% y - wektor kolumnowy zmiennej losowej Y
%
% Sprawdzone w srodowisku MATLAB 5.x
%
%tic
if exist('todo')==0 | isempty(todo)
todo='mean';
end
step=x(2)-x(1);
PX=fft(px,length(px).*N);
PY=PX.*step;
PY=PY.^(N-1);
PY=PY.*PX;
if strcmp(todo, 'mean')
y=x;
py=N.*abs(ifft(PY));
else
y=x.*N;
py=abs(ifft(PY));
end
%decimate 'py' N times
py=py(1:N:length(py));
%toc

122
LITERATURA:
1. Brandt S.: "Analiza danych - metody statystyczne i obliczeniowe", PWN,
Warszawa 1998
2. Czekała Z.: "Parada radarów", Dom Wydawniczy BELLONA, Warszawa 1999
3. Hellwig Z.: "Elementy rachunku prawdopodobieństwa i statystyki
matematycznej", PWN, Warszawa 1980, wydanie dziewiąte
4. Helstrom C. W.: "Statystyczna teoria detekcji", WNT, Warszawa 1964
5. Kącki T., Szyszkiewicz J., Majewski T., Słomiński L.: "Statystyczna teoria
radiolokacji", Wydział Wydawniczy WAT, Warszawa 1966
6. Knoch L., Ekiert T.: "Modulacja i detekcja", WKŁ, Warszawa 1979
7. Mrozek B., Mrozek Z.: "MATLAB, uniwersalne środowisko do obliczeń
naukowo-technicznych", Wydawnictwo PLJ, Warszawa 1996
8. Pacut A.: "Prawdopodobieństwo - teoria, modelowanie probabilistyczne w
technice", WNT, Warszawa 1985
9. Papoulis A.: "Prawdopodobieństwo, zmienne losowe i procesy stochastyczne",
WNT, Warszawa 1972
10. Seidler J.: "Statystyczna teoria odbioru sygnałów", PWN, Warszawa - Wrocław
1963
11. Skolnik M. I.: "Radar Handbook", Mc Graw-Hill, New York 1970
12. Smirnow N. W., Dunin-Barkowski I. W.: "Kurs rachunku prawdopodobieństwa i
statystyki matematycznej dla zastosowań technicznych", PWN, Warszawa
1969, wydanie drugie
13. Szabatin J.: "Podstawy teorii sygnałów", WKŁ, Warszawa 1982
14. MATLAB 5.2 User’s Guide
Wyszukiwarka
Podobne podstrony:
wykł-śc, POGODA- to chwilowy stan atmosfery na pewnym obszarze, okre˙lony przez uk˙ad powi˙zanych ze
Analiza podstawowych uk+éad+-w dyskretnych
BUD PRZEGRODA, Sprawdzi˙ pod wzgl˙dem cieplno-wilgotno˙ciowym przegrod˙ budowlan˙ pionow˙ o nast˙puj
uk ad pokarmowy
ANALIZA PRZYCZYN WYBUCHU WYBRANEJ WOJNY NA 3 POZIOMACH
uk-ad krwionoÂny. aq, Biomedyczne podstawy rozwoju i wychowania
UK AD LIMFATYCZNY, rodzaje i zasady masażu
uk+éad kr¦ů+ enia
Generatory drgan sinusoidalnych1, Celem ˙wiczenia jest zapoznanie si˙ z wybranymi podstawowymi uk˙ad
PRZEGR 1, Sprawdzi˙ pod wzgl˙dem cieplno-wilgotno˙ciowym przegrod˙ budowlan˙ pionow˙ o nast˙puj˙cym
TEATR OPRACOWANIA I sem, Raszewski- Uk+éad S, Raszewski - układ S
LABORATORIUM-NAPĘDÓW ELEK, Naped, UK˙AD DO REGULACJI PR˙DKO˙CI OBROTOWEJ
Parkinsonizm - drżączka poraźna, Parkinsonizm - dr˙˙czka pora˙na - jest to zesp˙˙ chorobowy charakte
Anatomia Uk%c5%82ad krwiotw%c3%b3rczy 06 notatki
Patologia Uk%c5%82ad kr%c4%85%c5%bcenia 03 notatki
Uk éad krwiono Ťny i ch éonny
UK AD KRWIONO NY I CH ONNY, rozwiązania z dopytek
8 6, 1. POMIARY W UK˙ADZIE SZEREGOWYM RLC.
więcej podobnych podstron