AGH , Wydz. EAIiE Katedra Automatyki Napędu i Urządzeń Przemysłowych			Imię , nazwisko : JAROSŁAW GANDZEL
TEORIA STEROWANIA I TECHNIKA REGULACJI			Semestr : letni.
Rok akademicki : 1998 / 99	Rok studiów : II		Grupa : II
Kierunek : ELEKTROTECHNIKA			środa , godz . 10^00 .
Temat ćwiczenia : Układy wielowymiarowe .			Nr ćwiczenia : 8 .
Data wykonania ćwiczenia : 10.03.1999.		Data zaliczenia sprawozdania :

1. Model matematyczny silnika w przestrzeni stanu :

Zmienne stanu: x₁ = ω(t) x₂ = i(t)

Sterowania: u₁ = u(t) u₂ = M_m.(t)

Wyjścia: y₁ = i(t) y₂ = ω(t)

Równania stanu :

1.1. Macierzowe równania stanu:

2. Schemat blokowy opisujący dynamikę silnika :

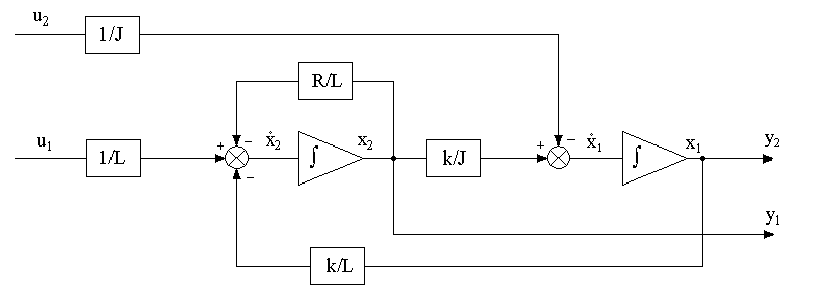
3. Wyznaczenie transmitancji zastępczej układu :

Transmitancje zastępczą układuwyliczam z poniższego wzoru :

Co w rezultacie daje :

3.1. Określenie poszczególnych transmitancji :

Schemat blokowy MIMO:

Dalsze obliczenia dokonywane są dla następujących danych :

R = 1,2[Ω] L = 0,2 [H] n_N = 900[obr./min] I_N = 70 [A]

U_N = 220 [V] J = 8 [kg⋅m²]

4.1. Postać równań stanu silnika na macierzach ABCD - wartości numeryczne:

4.2. Postać numeryczna transmitancji G­_IU , G_IM , G_ωU , G_ωM :

4.3. Transmitancja G_Z(s) wyznaczona przy pomocy funkcji „ss2tf „ :

Transmitancje wymuszeniowe :

num(1) 5 s num(2) 0,9018

---------- = ----------------------- ---------- = ------------------------

den s^2 + 6 s + 1.301 den s^2 + 6 s + 1.301

Transmitancje zakłóceniowe:

num(1) 0.9018 num(2) -0.125 s - 0.75

---------- = ----------------------- ---------- = ------------------------

den s^2 + 6 s + 1.301 den s^2 + 6 s + 1.301

Z porównania transmitancji w pkt. 4.2 i 4.3 wnioskujemy iż transmitancja zastępcza wyliczona za pomocą funkcji matlaba „ss2tf” i składa się z dwóch par transmitancji równych G_IM i G_ωM czyli transmitancjom wymuszeniowym : prądowej oraz prędkościowej oraz G_IU i G_ωU czyli transmitancjom zakłóceniowym : prądowej oraz prędkościowej .

5. Odpowiedź układu opisanego macierzami ABCD na skok jednostkowy :

6. Przebiegi będące odpowiedziami na skok jednostkowy transmitancji G­_IU,G_IM,G_ωU,G_ωM :

Na podstawie powyższych charakterystyk wnioskujemy iż w czasie załączenia zasilania początkowo prąd gwałtownie rośnie a następnie maleje do zera , natomiast prędkość rośnie i ustala się na pewnym poziomie . Odpowiedzi na zakłócenie uwidaczniają nam , że wzrost momentu powoduje zmniejszenie prędkości obrotowej silnika oraz zwiększenie prądu płynącego przez uzwojenia . Odpowiedzi układu są zgodne z oczekiwaniami .

7. Stałe czasowe silnika w postaci numerycznej:

Te = 0,1667 Tm =4,6107

8. Odpowiedź układu opisanego macierzami ABCD przy użyciu funkcji „ lsim „ dla następujących sygnałów wejściowych :

t_sym = (0 ; 2⋅t_k) gdzie: t_k = max(Te ; Tm) ⋅ 20;

Z powyższej odpowiedzi układu widać zmiany prądu i prędkości obrotowej zarówno przy rozruchu silnika i wyłączeniu zasilania jak i przy załączaniu i wyłączeniu obciążenia. Szczególnie ciekawe jest zachowanie się prądu w momencie wyłączenia zasilania .Prąd gwałtownie rośnie w kierunku przeciwnym co jest zgodne z zasadą przekory ( prąd stara się podtrzymać obracanie się silnika ) .Co jest zgodne z oczekiwaniami .

9. Wyznaczenie transmitancji G­_IU , G_IM , G_ωU , G_ωM przy zastosowaniu przekształceń Laplace'a:

9.1 Transmitancje G­_IU , G_IM , G_ωU , G_ωM w postaci symbolicznej :

9.2. Poszczególne transmitancje w postaci symbolicznej z wykorzystaniem stałych czasowych :

9.3. Poszczególne transmitancje w postaci TF :

9.4. Poszczególne transmitancje w postaci ZP :

Z porównania transmitancji z pkt. 4.2 z powyższymi wynikami wnioskujemy iż różnią się one między sobą ponieważ matlab nie potrafi skracać licznika i mianownika przez wspólny czynnik np:. liczbę lub „s” .Jeśli otrzymane wyniki z pkt. 9.3 sami uprościmy to uzyskamy identyczne transmitancje jak w pkt. 4.2 .

10. Przebiegi i(t) i ω(t) dla różnych wartości parametrów silnika przy następujących sygnałach wejściowych :

żółty - u(t) = U_N⋅1(t) oraz różowy - M._m.(t) = 0

1. czerwony - R₀=R ; niebieski - R₁=0,5R ; zielony - R₂=2R :

2. czerwony - L₀=L ; niebieski - L₁=0,05L ; zielony - L₂=10L :

3. czerwony - J₀=J ; niebieski - J₁=0,1J ; zielony - J₂=5J :

Z powyższych wykresów wnioskuję , że im większa rezystancja tym mniejsza jest wartość prądu rozruchowego i większa jest prędkość obrotowa silnika .Natomiast stała czasowa wykresu ω(t) rośnie wraz ze wzrostem rezystancji .

Zmiana indukcyjności nieznacznie wplywa na przebieg ω(t) .Duża indukcyjność zmniejsza prąd rozruchowy , ale już nie w tak istotny sposób jak zwiekszenie rezystancji.Co ciekawe dla indukcyjności 0.2 i 0.01 [H] obie charakterystyki mają podobny przebieg .

Zwiększenie momentu bezwładności wpływa ujemnie na właściwości dynamiczne silnika - warunek równowagi osiągany jest po dużo dłuższym czasie.

1

8

---