POLITECHNIKA ŁÓDZKA
FILIA W BIELSKU - BIAŁEJ
wydz. F.T.I. i M.S.
kierunek: INFORMATYKA
semestr: II
grupa nr 208
ĆWICZENIE NR 56
BADANIE WPŁYWU TEMPERATURY NA PRZEWODNICTWO ELEKTRYCZNE CIAŁ STAŁYCH.
Wykonali :
Bartosz Korczyk
Krzysztof Ślemp
Grzegorz Frej
I. Wprowadzenie teoretyczne i opis stanowiska doświadczalnego :
Model pasmowy przewodnictwa.
Ze względu na przewodnictwo elektryczne wszystkie ciała dzielimy na : izolatory, przewodniki i półprzewodniki. Izolatory są bardzo złymi przewodnikami. Przewodniki mają bardzo mały opór właściwy rzędu 10-8-10-6 . Opór właściwy półprzewodników mieści się w bardzo szerokich granicach od 10-7 do 108 , lecz nie sama wartość oporu właściwego jest podstawą klasyfikacji. Istotnym czynnikiem jest temperaturowa zależność oporu elektrycznego : w przewodnikach opór rośnie z temperaturą, a w półprzewodnikach - na odwrót, opór maleje wraz ze wzrostem temperatury. Poszczególne grupy różnią się mechanizmem przewodzenia prądu. W metalach, w których atomy są zlokalizowane w sieci krystalicznej, zewnętrzne elektrony są zupełnie wolne i mogą poruszać się swobodnie w całej objętości kryształu - metalu. W półprzewodnikach zewnętrzne elektrony są słabo związane z atomami zlokalizowanymi w sieci, stąd różne czynniki zewnętrzne mogą je uwolnić, a uwolnione elektrony mogą być nośnikami prądu. Rozpiętość zmienności oporu półprzewodników wynosi aż 15 rzędów wielkości, stąd i mechanizmy przewodzenia są bardzo zróżnicowane.
Teoria pasmowa ciał stałych - opisuje zmianę poziomów energetycznych atomów lub cząstek w przypadku utworzenia przez nich struktury krystalicznej. W swobodnych atomach elektrony nie mogą mieć dowolnych wartości energii lecz przyjmują niektóre wartości dozwolone przez reguły kwantowe, tzn. że poziomy energetyczne są oddzielone od siebie dość szerokimi odstępami o wzbronionych wartościach energii. Często energetyczne poziomy dozwolone przedstawiamy za pomocą poziomych kresek. Osią rzędnych jest energia. Położenie każdej kreski oznacza energię danego stanu. Odstępy między kreskami odpowiadają wzbronionym wartościom energii.
a) b)
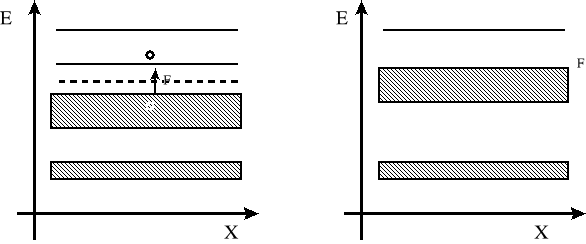
Rys.1. Model pasmowy : a) półprzewodnika, b) przewodnika.
Półprzewodnictwo samoistne.
Czysty, zbliżony do idealnego kryształ półprzewodnika wykazuje przewodnictwo samoistne.
Schemat pasm energetycznych półprzewodnictwa samoistnego w temp. 0K przewodnictwo jest równe zeru, wszystkie stany w paśmie walencyjnym są zapełnione i wszystkie stany w paśmie przewodnictwa są puste. Gdy rośnie temperatura, przewodnictwo również wzrasta, gdyż elektrony są termicznie wzbudzone do pasma przewodnictwa. (rys.1a.)
Przewodnictwo domieszkowe.
Kryształ rzeczywisty różni się od idealnego tym, że występują w nim centra domieszkowe tzw. defekty punktowe.
Centra domieszkowe mogą być kilku typów charakteryzujących się :
występowaniem obcych atomów,
odstępstwami od składu stechiometrycznego (pewnych atomów może być więcej a innych mniej),
pustymi węzłami w sieci krystalicznej,
dodatkowymi atomami lub jonami w obszarach międzywęzłowych,
możliwe są też defekty liniowe lub śrubowe, tzw. dyslokacje.
II. Praktyczne wykonanie ćwiczenia :
Przyrządy:
-termostat;
-płytki z badanymi elementami w kąpieli olejowej;
-omomierz;
-termometr;
Do wyprowadzeń badanych elementów umieszczonych w termostacie przyłączono przygotowane urządzenia do pomiaru oporności (ohmomierz'e). Odczytano temp. początkową kąpieli olejowej T0 i zmierzono wartość oporności początkowych R0 badanych elementów. Następnie włączono grzałkę na maksymalną moc. Gdy temperatura kąpieli olejowej osiągnęła pełną wartość (25oC) dokonano kolejnych pomiarów, w 5-cio stopniowych odstępach między kolejnymi wartościami temperatury oleju. Badania zakończono przy temp. 80oC. Następnie wyłączono ogrzewanie kąpieli. Zmierzone wartości badanych parametrów umieszczono w tabelach.
III. Wyniki pomiarów oraz obliczeń :
L.p. 1 - odpowiada pomiarowi w temperaturze otoczenia.
1)Przewodnik:
l.p. |
t |
T |
ΔT |
R |
ΔR |
R/R0 |
|
[0C] |
[K] |
[K] |
[Ω] |
[Ω] |
|
1 |
19 |
292 |
0 |
19,95 |
0 |
1 |
2 |
25 |
298 |
6 |
20,20 |
0,25 |
1,01 |
3 |
30 |
303 |
11 |
20,56 |
0,61 |
1,03 |
4 |
35 |
308 |
16 |
21,01 |
1,06 |
1,05 |
5 |
40 |
313 |
21 |
21,41 |
1,46 |
1,07 |
6 |
45 |
318 |
26 |
21,79 |
1,84 |
1,09 |
7 |
50 |
323 |
31 |
22,12 |
2,17 |
1,11 |
8 |
55 |
328 |
36 |
22,42 |
2,47 |
1,12 |
9 |
60 |
333 |
41 |
22,72 |
2,77 |
1,14 |
10 |
65 |
338 |
46 |
22,88 |
2,93 |
1,15 |
11 |
70 |
343 |
51 |
23,05 |
3,10 |
1,16 |
12 |
75 |
348 |
56 |
23,39 |
3,44 |
1,17 |
13 |
80 |
353 |
61 |
23,78 |
3,83 |
1,19 |
a=0,0032 |
± 0,0001 |
b=1,00 |
± 0,01 |
Wsp. prostej regresji |
2)Półprzewodnik:
l.p. |
t |
T |
1/T |
R |
ΔR |
ln R |
|
[oC] |
[K] |
[K-1] |
[kΩ] |
[kΩ] |
|
1 |
19 |
292 |
0,0034 |
12,05 |
0 |
2,49 |
2 |
25 |
298 |
0,0034 |
8,64 |
-3,41 |
2,16 |
3 |
30 |
303 |
0,0033 |
6,91 |
-5,14 |
1,93 |
4 |
35 |
308 |
0,0032 |
5,52 |
-6,53 |
1,71 |
5 |
40 |
313 |
0,0032 |
4,46 |
-7,59 |
1,50 |
6 |
45 |
318 |
0,0031 |
3,59 |
-8,46 |
1,28 |
7 |
50 |
323 |
0,0031 |
2,96 |
-9,09 |
1,09 |
8 |
55 |
328 |
0,0030 |
2,46 |
-9,59 |
0,90 |
9 |
60 |
333 |
0,0030 |
2,04 |
-10,01 |
0,71 |
10 |
65 |
338 |
0,0030 |
1,73 |
-10,32 |
0,55 |
11 |
70 |
343 |
0,0029 |
1,5 |
-10,55 |
0,41 |
12 |
75 |
348 |
0,0029 |
1,29 |
-10,76 |
0,25 |
13 |
80 |
353 |
0,0028 |
1,12 |
-10,93 |
0,11 |
a=4004 |
±49 |
b=-11,28 |
± 0,03 |
Wsp. prostej regresji |
IV . Wyniki obliczeń:
Wykreślone proste regresji R/R0 = f(ΔT) i ln(R) = f(1/T) pozwalają wyznaczyć ich wsp. a i b, a co za tym idzie odpowiadające im parametry α, E/k, E, Rpo
1)Przewodnik
Opór elektryczny przewodnika:
R=Ro(1+αΔT) [Ω]
Ro- opór elektryczny przewodnika w temperaturze otoczenia;
ΔT- przyrost temperatury;
α-temperaturowy współczynnik rezystancji.
![]()
Równanie opisujące zależność R/R0 = f(ΔT)
Y = ax + b
α = a = 0,0032 [K-1]
R/R0(ΔT=0) |
α±Δၡ |
|
[K-1] |
1 |
0,0032Ⴑ0,0001 |
2)Półprzewodnik:
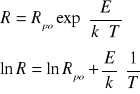
Równanie zależności ln(R) = f(1/T
E - szerokość pasma wzbronionego;
k - stała Boltzmann'a (k=1,38⋅10-23 [J/K]);
Rpo - stała oporności.
lnRpo =b ⇒ Rpo = eb = e-11,28 = 1,26⋅10-5 [Ω]
E/k = a ⇒ E = k⋅a = 1,38⋅10-23 ⋅ 4004 = 5,53⋅ 10-20 [J]
1eV = 1,58⋅10-19
E = ![]()
Rpo |
E/k |
E |
[Ω] |
[K] |
[eV] |
1,26⋅10-5 |
4004±49 |
0,35 |
V . Wnioski :
Rezystancja przewodnika rośnie (nieznacznie) wraz ze wzrostem temperatury,
W przypadku półprzewodnika sytuacja jest odwrotna. Jednak rezystancja półprzewodnika spada około dziesięciokrotnie.
6
Wyszukiwarka
Podobne podstrony:
cwicz56 nowe, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
w.85, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 40, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
cwiczenie61a, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
FIZYKA75, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
F-85, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
tabele do cw 36, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 13, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
CW85GRZ, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
LAB3 61, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
lab cw12, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
jola 66, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 85, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 56, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
sciaga fizyka kolos 1a, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
FIZYK 75, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
FIZYK 61, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
więcej podobnych podstron