Simpleks - zawsze na max. Jeśłi jest min to mnożymy (-1)

Jeżeli w końcowej tablicy simpleks współczynniki optymalności (c-z) są mniejsze bódź równe 0 a w bazie pozostaje zmienna sztuczna to zadanie jest sprzeczne.

Jeżeli w kolumnie do wprowadzenia nie ma dodatnich wartości to funkcja jest nieograniczona od góry.

Jeżeli w ostatniej tablicy simpleks mamy większą liczbę c-z niż jest zmiennych bazowych to istnieją wtedy rozwiązania alternatywne.

Przy sprowadzaniu do postaci bazowej jest \< dodajemy zmienną bilansującą a jeśli jest >/ odejmujemy zmienną bilansującą oraz dodajemy zmienną sztuczną. W przypadku równości dodajemy tylko zmienną sztuczną.

Np. dla x1 c-z = wartość dla x1 - (ci * x12 + ci *x13 ...)

Do bazy wpisujemy te x, które nie mają w kolumnie żadnych ujemnych wartości. Należy to zrobić tak aby można było utworzyć macierz jednostkową.

Gdy wprowadzamy nową zmienną a stara opuszcza bazę tworzymy po wpisaniu macierz jednostkową w tej kolumnie a resztę przekształcamy tak aby było możliwe jej utworzenie.

Metoda konta płn-zach:

1. sprawdzić, czy jest zbilansowane.

2. pierwsze rozwiązanie dopuszczalne w tabeli metoda konta płn-zach.

3. w tabeli kosztów zaznaczamy elementy bazowe (*) i dla nich wyliczamy u i v. Obliczamy wskaźniki optymalności

4. Jeżeli wskaźniki optymalności są ujemne, wybieramy najmniejszy i tą komórkę wprowadzamy do bazy (wg cyklu)

5. znajdujemy w cyklu (ujemnym!) najmniejszą i o nią modyfikujemy przewóz

6. Należy to powtarzać aż w tablicy kosztów nie będzie ujemnych wartości

Zawsze w zadaniu transportowym ilość węzłów wyznaczamy ze wzoru: m+n-1, gdzie m - ilość dostawców (wiersze), n - ilość odbiorców (kolumny)

Podczas wyznaczania tablicy kosztów U₁ = 0, koszty dla wartości niezerowych (bazowych) są zerem, pozostałe wyliczamy z u i v.

Metoda PERT (obliczenie czasu oczekiwanego)

Prawdopodobieństwo czasu zadanego

Wariancja δ każdego elementu

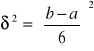
Odchylenie standardowe

---