RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE - DLA BIOTECHNOLOGII (III r.)

(wg Tichonowa i Samarskiego)

Klasyfikacja równań różniczkowych cząstkowych drugiego rzędu

o dwóch zmiennych niezależnych ze względu na postać równania.

Równanie różniczkowe cząstkowe drugiego rzędu z dwiema zmiennymi niezależnymi x,y i funkcją niewiadomą u ma postać:

F(x, y, u, u_x, u_y, u_xx, u_xy, u_yy)=0.

W szczególności, równanie quasi-liniowe (prawie liniowe) ma postać:

a₁₁(x, y, u, u_x, u_y)u_xx + 2a₁₂(x, y, u, u_x ,u_y)u_xy + a₂₂(x, y, u, u_x ,u_y)u_yy +

+ F₁(x, y, u, u_x ,u_y)=0.

W szczególności, równanie liniowe względem najstarszych pochodnych:(1) a₁₁(x,y)u_xx + 2a₁₂(x,y)u_xy + a₂₂(x,y)u_yy + F₁(x, y, u, u_x ,u_y) = 0.Wreszcie - równanie liniowe ma postać:

a₁₁(x,y)u_xx + 2a₁₂(x,y)u_xy + a₂₂(x,y)u_yy + b₁(x,y)u_x + b₂(x,y)u_y + c(x,y)u +

+ f(x,y) = 0.

W szczególności - równanie liniowe o stałych współczynnikach to równanie

a₁₁u_xx + 2a₁₂u_xy + a₂₂u_yy + b₁u_x + b₂u_y + cu + f = 0.

Dalszej klasyfikacji dla równań liniowych względem najstarszych pochodnych, tzn.

a₁₁(x,y)u_xx + 2a₁₂(x,y)u_xy + a₂₂(x,y)u_yy + F₁(x, y, u, u_x ,u_y) = 0.

możemy dokonać ze względu na sygnaturę formy kwadratowej ∑a_ijξ_iξ_j.

W tym celu wykonujemy przejście do nowych zmiennych niezależnych ξ i η:

ξ=ξ(x,y), η=η(x,y)

przy czym zakładamy, że odwzorowanie to jest w pewnym obszarze płaszczyzny rozwiązywalne, tak że można również napisać

x=x(ξ,η), y=y(ξ,η);

zakładamy ponadto, że jakobian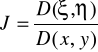
jest różny od zera w rozpatrywanym obszarze.

Otrzymujemy:

u_x = u_ξξ_x + u_ηη_x u_y = u_ξξ_y + u_ηη_y;

biorąc w pierwszym z tych wzorów u_ξ zamiast u, dostajemy (u_ξ)_x =u_ξξξ_x +u_ξηη_x ; podobnie (u_ξ)_y =u_ξξξ_y + u_ξηη_y , (u_η)_x =u_ηξξ_x +u_ηηη_x , (u_ξη)_y =u_ηξξ_y +u_ηηη_y.

Wobec tego

u_xx = (u_ξξ_x + u_ηη_x)_x = (u_ξ)_xξ_x + u_ξξ_xx + (u_η)_xη_x + u_ηη_xx =

(u_ξξξ_x +u_ξηη_x)ξ_x + u_ξξ_xx + (u_ηξξ_x +u_ηηη_x)η_x + u_ηη_xx ,

czyli

u_xx = u_ξξ(ξ_x)² +2u_ξηξ_xη_x +u_ηη(η_x)² + u_ξξ_xx + u_ηη_xx.

Podobnie

u_xy = u_ξξξ_xξ_y +u_ξη(ξ_xη_y + ξ_yη_x) +u_ηηη_xη_y + u_ξξ_xy + u_ηη_xy,

wreszcie

u_yy = u_ξξ(ξ_y)² +2u_ξηξ_yη_y +u_ηη(η_y)² + u_ξξ_yy + u_ηη_yy.

Podstawiając powyższe wyrażenia do wyjściowego równania, dostajemy równanie

postaci:

gdzie

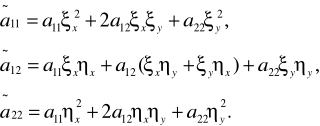
przy czym funkcja F^~ nie zależy od drugich pochodnych.

Zauważmy, że wzór na
jest analogiczny do wzoru na
- otrzymany przez zastąpienie ξ przez η. Postaramy się dobrać funkcje ξ=ξ(x,y) i ewentualnie η=η(x,y) tak, aby współczynniki
i ewentualnie
stały się równe zeru.

Rozważmy równanie różniczkowe cząstkowe pierwszego rzędu

(5) a₁₁(z_x)² +2a₁₂z_xz_y +a₂₂(z_y)² = 0.

Niech z=ϕ(x,y) będzie jakimkolwiek rozwiązaniem tego równania. Jeśli położyć ξ=ϕ(x,y), to współczynnik
będzie oczywiście równy zeru. Tak więc zadanie doboru nowych zmiennych ξ i η tak, aby równanie przybrało jak najprostszą formę, jest związane z rozwiązaniem równania (5).

Lemat: z=ϕ(x,y) jest szczególnym rozwiązaniem równania (5) wtedy i tylko wtedy, gdy ϕ(x,y)=C jest całką ogólną następującego równania różniczkowego:

(6) a₁₁ dy² - 2a₁₂ dx dy + a₂₂ dx² = 0,

czyli przy założeniu, że y można traktować jako funkcję x,

(6)
.

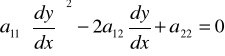
Dowód: (⇒) Niech z=ϕ(x,y) będzie pewnym rozwiązaniem równania (5), tzn. zachodzi tożsamość

czyli też (przy założeniu że ϕ_y≠0) tożsamość

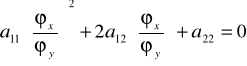
dla każdego (x,y) z obszaru, gdzie to rozwiązanie jest określone. Chcemy pokazać, że ϕ(x,y)=C jest całką ogólną równania (6), tzn. dla każdego C funkcja uwikłana y=f(x,C) wyznaczona z równania ϕ(x,y)=C (czyli spełniająca ϕ(x,f(x,C))=C), spełnia równanie (6). Ale dla tej funkcji mamy (ze znanych własności funkcji uwikłanej)

.

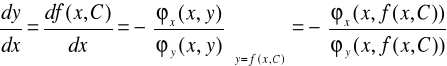
Stąd wyliczamy, że

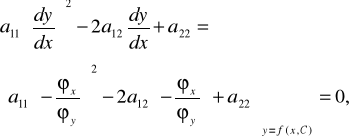
bo, jak wspomniano wyżej, wyrażenie w nawiasach kwadratowych jest równe zeru dla dowolnych wartości x,y w obszarze określoności rozwiązania - a więc w szczególności dla (x,y) = (x,f(x,C)). Otrzymana równość dowodzi, że v(x,y) jest rzeczywiście całką ogólną równania (6).

(⇐) Niech teraz ϕ(x,y)=C będzie całką ogólną równania (6), tzn. dla każdego C funkcja uwikłana y=f(x,C) wyznaczona z równania ϕ(x,y)=C spełnia równanie (6), tzn.

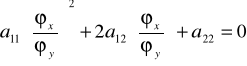
w każdym punkcie postaci (x,f(x,C)). Chcemy pokazać, że

w badanym obszarze, tzn. w każdym punkcie (x₀,y₀) tego obszaru. Ale z faktu, że ϕ(x,y)=C jest całką ogólną wynika, że dla pewnej wartości C₀ (mianowicie, C₀=ϕ(x₀,y₀)) krzywa y=f(x,C₀) przechodzi przez punkt (x₀,y₀), tzn. y₀ =f(x₀,C₀). Dla wszystkich punktów (x,f(x,C₀)) tej krzywej mamy

,

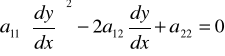
tzn.

.

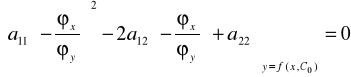
W szczególności podstawiając tu x=x₀, mamy

,

c.n.d.

Równanie (6) nazywamy równaniem charakterystycznym dla równania (1), a jego całki - charakterystykami równania (1).

Kładąc ξ=ϕ(x,y), gdzie ϕ(x,y)=const jest całką ogólną równania (6), zerujemy współczynnik przy u_ξξ . Jeżeli ψ(x,y) jest inną całką ogólną równania (6), niezależną od ϕ(x,y) (w tym sensie, że jakobian tego układu funkcji jest różny od zera w rozpatrywanym obszarze), to kładąc η=ψ(x,y) otrzymamy wyzerowanie się także współczynnika przy u_ηη .

Równanie (6) rozpada się (w przypadku a₁₁≠0) na dwa równania:

(9)
,

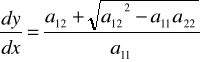
(10)
.

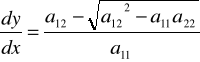
Znak wyrażenia pod pierwiastkiem określa typ wyjściowego równania

(1) a₁₁(x,y)u_xx + 2a₁₂(x,y)u_xy + a₂₂(x,y)u_yy + F₁(x, y, u, u_x ,u_y) = 0.

Równanie to będziemy nazywać w punkcie M równaniem:

1. typu hiperbolicznego, jeżeli w punkcie M (a₁₂)² -a₁₁a₂₂ > 0 ;

2. typu eliptycznego , jeżeli w punkcie M (a₁₂)² -a₁₁a₂₂ < 0 ;

3. typu parabolicznego , jeżeli w punkcie M (a₁₂)² -a₁₁a₂₂ = 0 .

Można wykazać, że [(a₁₂)² -a₁₁a₂₂]_{z wężykami}= D² [(a₁₂)² -a₁₁a₂₂] , skąd wynika niezmienność typu równania przy zmianie zmiennych niezależnych. W różnych punktach obszaru równanie może mieć różny typ.

Rozpatrzmy obszar G, w którego wszystkich punktach równanie ma ten sam typ. Przez każdy punkt obszaru G przechodzą dwie charakterystyki, przy czym dla równania hiperbolicznego charakterystyki są rzeczywiste i różne, dla równania eliptycznego są zespolone i różne, a dla równania parabolicznego obie charakterystyki są rzeczywiste i pokrywają się ze sobą.

Przypadek 1. Równanie hiperboliczne. Prawe części równań (9) i (10) są rzeczywiste i różne. Całki ogólne ϕ(x,y)=C i ψ(x,y)=D określają rzeczywiste rodziny charakterystyk. Kładąc

(11) ξ=ϕ(x,y), η=ψ(x,y)

otrzymujemy przekształcenie o niezerowym jakobianie (gdyby bowiem jakobian był równy zeru, to wiersze wyznacznika musiałyby być proporcjonalne, tzn.

,

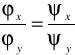
co jest jednak niemożliwe, albowiem

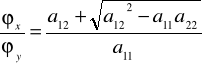
i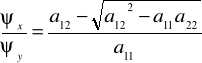

- przyjęliśmy tu a₁₁≠0, co nie ogranicza ogólności). Ze sposobu wyboru tego przekształcenia wynika, że w równaniu przekształconym współczynniki przy u_ξξ i u_ηη będą równe zeru. Po podzieleniu przez współczynnik przy u_ξη doprowadzamy równanie (4) do postaci

u_ξη = Φ(ξ,η,u,u_ξ,u_η), gdzie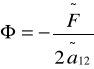
.

Jest to tak zwana postać kanoniczna równania hiperbolicznego. Niekiedy używa się też innej postaci kanonicznej. Mianowicie, kładąc

ξ = α + β , η = α - β

czyli

α = (ξ + η)/2 , β = (ξ - η)/2,

gdzie α,β - nowe zmienne - otrzymujemy

u_ξ =(u_α + u_β)/2 , u_η =(u_α - u_β)/2 , u_ξη =(u_αα - u_ββ)/4.

W rezultacie równanie (4) przyjmie postać:

u_αα - u_ββ = Φ₁ (Φ₁ = 4Φ).

Przypadek 2. Równanie paraboliczne. Mamy wtedy tylko jedną całkę ogólną: ϕ(x,y)=C. Połóżmy w tym przypadku

ξ=ϕ(x,y), η=ψ(x,y),

gdzie ψ(x,y) - dowolna funkcja, niezależna od ϕ, tzn. taka, aby jakobian przekształcenia był niezerowy: wystarczy wziąć np. ψ=x lub ψ=y. Nasz wybór ϕ zapewnia, że współczynnik a^~₁₁ się zeruje. Ale

0 = a^~₁₁ = a₁₁ξ_x² + 2a₁₂ξ_xξ_y + a₂₂ξ_y² = ±(√|a₁₁| ξ_x + √|a₂₂| ξ_y)²

(ostatnia równość wynika z tego, że (a₁₂)² =a₁₁a₂₂ - tak więc współczynniki a₁₁ i a₂₂ mają ten sam znak; jeżeli są dodatnie, to bierzemy "+", jeżeli ujemne - bierzemy "-"). Stąd jednakże wynika, że także

a^~₁₂ =a₁₁ξ_xη_x +a₁₂(ξ_xη_y + ξ_yη_x)+a₂₂ξ_yη_y =±(√|a₁₁| ξ_x + √|a₂₂| ξ_y)(√|a₁₁| η_x + √|a₂₂| η_y)=0

Po podzieleniu równania (4) przez współczynnik przy u_ηη otrzymamy postać kanoniczną dla równania parabolicznego:

u_ηη = Φ(ξ, η, u, u_ξ, u_η), gdzie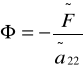
.

Jeżeli do prawej części nie wchodzi u_ξ , to będzie to zwykłe równanie różniczkowe, w którym ξ występuje jako parametr.

Przypadek 3. Równanie eliptyczne. W tym przypadku prawe strony równań (9) i (10) są zespolone. Niech

ϕ(x,y) = C

- zespolona całka ogólna równania (9). Wtedy

ϕ*(x,y) = D,

gdzie ϕ* - funkcja sprzężona z ϕ, jest również całką ogólną równania (10). Przejdźmy do zmiennych zespolonych, kładąc

ξ=ϕ(x,y), η=ϕ*(x,y).

Wtedy równanie typu eliptycznego sprowadza się do takiej samej postaci, jak hiperboliczne. Jednakże, chcąc uniknąć zmiennych zespolonych, wprowadzamy nowe zmienne α i β, dane wzorami

α= (ϕ + ϕ*)/2 , β= (ϕ - ϕ*)/(2i) ,

tak że

ξ = α + iβ, η = α - iβ.

W tym przypadku, znów z wyboru ϕ,

a^~₁₁ = a₁₁ξ_x² + 2a₁₂ξ_xξ_y + a₂₂ξ_y² =

= (a₁₁α_x² + 2a₁₂α_xα_y + a₂₂α_y²) - (a₁₁β_x² + 2a₁₂β_xβ_y + a₂₂β_y²)

+ 2i[a₁₁α_x a₁₁α_xβ_x + a₁₂(α_xβ_y + α_yβ_x) + a₂₂α_yβ_y] = 0

tzn. w zmiennych α i β mamy

a^~₁₁ = a^~₂₂ i a^~₁₂ = 0.

Równanie (4) po podzieleniu przez współczynnik przy u_αα przyjmie postać

u_αα +u_ββ = Φ(α,β,u,u_α ,u_β ) (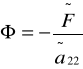
).

(Uwaga: współczynniki występujące w równaniu muszą być analityczne, aby dały się w sposób naturalny określić także dla argumentów zespolonych.)

Zob. plik „Równania paraboliczne.doc”

Klasyfikacja równań różniczkowych cząstkowych II rzędu - Str. 4 z 8

---