Przedział ufności dla wartości oczekiwanej (średniej) ze znanym odchyleniem standardowym.
Estymatorem wartości oczekiwanej (średniej) jest średnia arytmetyczna z próby ![]()
, która ma rozkład ![]()
. Po standaryzacji zmiennej ![]()
statystyka
![]()
ma rozkład normalny ![]()
.
Przedział ufności dla wartości oczekiwanej (średniej):
![]()
gdzie:
![]()
- wartość odczytana z tablic rozkładu normalnego dla danego poziomu istotności α
![]()
- odchylenie standardowe w populacji generalnej
Przedział ufności dla wartości oczekiwanej (średniej) z nieznanym odchyleniem standardowym
Wykorzystujemy statystykę t o rozkładzie Studenta o n-1 stopniach swobody:
![]()
spełniona jest następująca zależność:
![]()
Przedział ufności dla wartości oczekiwanej (średniej) gdy n < 30:
![]()
gdzie:
![]()
- odchylenie standardowe z próby
![]()
- wartość odczytana z tablic rozkładu Studenta dla poziomu istotności α oraz n-1 stopni swobody
Gdy n > 30 wartość ![]()
, odczytaną z tablic rozkładu Studenta możemy zastąpić wartością ![]()
, odczytaną z tablic rozkładu normalnego oraz ![]()
.
Tak więc przedział ufności dla wartości oczekiwanej (średniej) ma postać (n >30):
![]()
Przedział ufności dla wariancji i odchylenia standardowego
Do budowy przedziału stosujemy statystykę ![]()
o n-1 stopniach swobody:
![]()
Dla danego współczynnika ufności 1-α istnieją wartości ![]()
![]()
spełniające zależność:
![]()
Przedział ufności dla wariancji ma postaci (n ≤ 30):
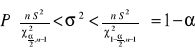
Przedział ufności dla odchylenia standardowego ma postać (n ≤ 30):
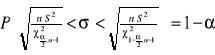
gdzie:
![]()
, ![]()
- wartości odczytane z rozkładu ![]()
dla n-1 stopni swobody
Przedział ufności dla odchylenia standardowego (n > 30):
![]()
gdzie:
![]()
- wartość odczytana z tablic rozkładu normalnego dla poziomu istotności α
Przedział ufności dla wskaźnika struktury (frakcji)
Przedział wyznaczamy gdy ![]()
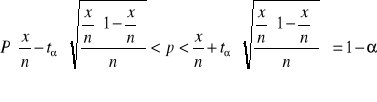
gdzie:
![]()
odczytujemy z tablic rozkładu normalnego tak, że ![]()
![]()
- liczba elementów próby spełniających dany warunek
![]()
- liczba wszystkich elementów próby
Wyszukiwarka
Podobne podstrony:
Cwiczenie 53c, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
Cwiczenie 11i, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
Cwiczenie 32f, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
Cwiczenie 0f, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEM
Wstep 0, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEMESTR
Zadania bilanse, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia,
Projekt 2 - Ewa Litwinek, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I
kryształy egzamin 2009, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I st
Pytanianakolosach, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia
Układ MgO-Al2O3-SiO2, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stop
wyniki zaliczenia w I term. gr 3.x, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stac
Sprawozdanie JP, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia,
Metody badan odpornosci korozyjnej, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stac
Całość, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEMESTR 2
Egzamin fizyka 31-35, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stop
Z5 - układ CaO-Al2O3-SiO2, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I
do druku lool, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
egzamin fizyka zrobione cz.1, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarn
pytania u komornickiego, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I s
więcej podobnych podstron