Aleksandra Hupka 157929
gr. PT TN 13:15-15:00
Metody numeryczne
Zad. 12
„Miejsca zerowe”
Treść zadania:
Miejsca zerowe- f(x)=(x-2)2. Wyznacz postać wzoru pk=g(pk-1) z metody siecznych. Startując z punktu p0=2.2 i p1=2.4 wyznacz ręcznie pierwsze trzy przybliżenia miejsca zerowego p1,p2,p3 metodą siecznych. Następnie wyznacz miejsca zerowe funkcji z dokładnością δ=0.001 (max1=30) używając odpowiedniego skryptu Matlaba dla tych punktów. Następnie użyj do wyznaczenia miejsca zerowego metody Newtona. Skomentuj wyniki i dokładność otrzymanych miejsc zerowych. Używając komendy plot zrób wykres funkcji f(x) na zadanym przedziale oraz zaznacz na nim ręcznie graficzną interpolację metody siecznych. Wydruk wykresu dołącz do sprawozdania.
Obliczanie trzech pierwszych przybliżeń miejsca zerowego funkcji:
![]()
Punkty startowe:
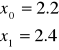
Wartość funkcji w punktach startowych:
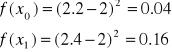
Kolejne przybliżenia miejsca zerowego funkcji:
![]()
Zatem
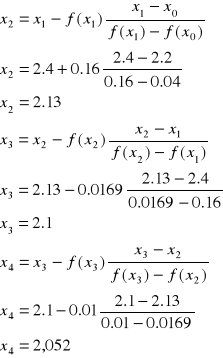
Rzeczywiste miejsce zerowe:
![]()
Obliczanie miejsca zerowego metodą siecznych za pomocą MatLaba:
Kod Matlaba:
xx=linspace(-2,3,200);
p0=2.2; p1=2.4;
delta=0.001; max1=30; tol=0.001;
[k, p, err, P, GP] = sieczne('f', p0, p1, delta, tol, max1)
k =
13
p =
2.0012
err =
7.6781e-004
P =
2.2000
2.4000
2.1333
2.1000
2.0571
2.0364
2.0222
2.0138
2.0085
2.0053
2.0033
2.0020
2.0012
GP =
0.0400
0.1600
0.0178
0.0100
0.0033
0.0013
0.0005
0.0002
0.0001
0.0000
0.0000
0.0000
0.0000
4.Obliczanie miejsca zerowego metodą Newtona za pomocą MatLaba:
function y=f(x)
y=(x-2).^2;
function y=df(x)
y=2*x-4
xs=linspace(-2,3);
p0=2.2;
delta=0.001; max1=30; tol=0.0000001;
[k, p, err, P, GP] = newton('f', 'df', p0, delta, tol, max1)
fx=xs.^2-4*xs+4;
plot(xs,fx);
legend('fx');
grid on
xs=linspace(-2,3);
p0=2.2;
delta=0.001; max1=30; tol=0.0000001;
[k, p, err, P, GP] = newton('f', 'df', p0, delta, tol, max1)
fx=xs.^2-4*xs+4;
plot(xs,fx);
legend('fx');
grid on
>> xs=linspace(-2,3);
p0=2.2;
delta=0.001; max1=30; tol=0.0000001;
[k, p, err, P, GP] = newton('f', 'df', p0, delta, tol, max1)
k =
9
p =
2.0008
err =
7.8125e-004
P =
2.2000
2.1000
2.0500
2.0250
2.0125
2.0063
2.0031
2.0016
2.0008
GP =
0.0400
0.0100
0.0025
0.0006
0.0002
0.0000
0.0000
0.0000
0.0000
5.Wykres:
Wnioski:
Z wyników powyżej wnioskuje, że obliczone ręcznie miejsca zerowe minimalnie różnią się od tych obliczonych w Matlabie. Wynika z obliczeń, że dla metody siecznych wynik iteracji wyniósł 13 a dla metody Newtona wyniósł 9. Zatem metoda „Newtona” jest dokładniejsza, ponieważ szybciej odnajduje miejsce zerowe.
Wyszukiwarka
Podobne podstrony:
czebyszew, OZE, Metody numeryczne, Metody numeryczne, Aleksandra Hupka 157929
miejsca zerowe, OZE, Metody numeryczne, Metody numeryczne, Cezary Winnik 157958
metody zad 3- dokonczyc, OZE, Metody numeryczne, Metody numeryczne, Zad 3
Wyprowadzenie wielomianów, OZE, Metody numeryczne, Metody numeryczne, Paulina Pietrasz
Metody numeryczne w6
metoda siecznych, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
MN energetyka zadania od wykładowcy 09-05-14, STARE, Metody Numeryczne, Część wykładowa Sem IV
METODA BAIRSTOWA, Politechnika, Lab. Metody numeryczne
testMNłatwy0708, WI ZUT studia, Metody numeryczne, Metody Numeryczne - Ćwiczenia
Metody numeryczne Metoda węzłowa
Metody numeryczne, wstep
metody numeryczne w4
Metody numeryczne PDF, MN macierze 01 1
Metody numeryczne w11
Metody Komputerowe i Numeryczne, Równania różniczkowe zwyczajne
metody numeryczne i w9
Metody Komputerowe i Numeryczne, Równania nieliniowe
więcej podobnych podstron