15. Zjawiska korpuskularno-falowe

15.1. Promieniowanie termiczne

Podstawowe źródła światła: - ogrzane ciała stałe lub gazy, w których zachodzi wyładowanie elektryczne.

Emisja ↔ absorpcja

R - widmowa zdolność emisyjna promieniowania

R dλ - szybkość z jaką jednostkowy obszar powierzchni wypromieniowuje energię z zakresu długości fal λ, λ+dλ.

Całkowita zdolność emisyjna promieniowania - szybkość z jaką jednostka powierzchni wypromieniowuje energię do przedniej półkuli:

(analogia do rozkładu Maxwella dla prędkości!)

Własności widma termicznego:

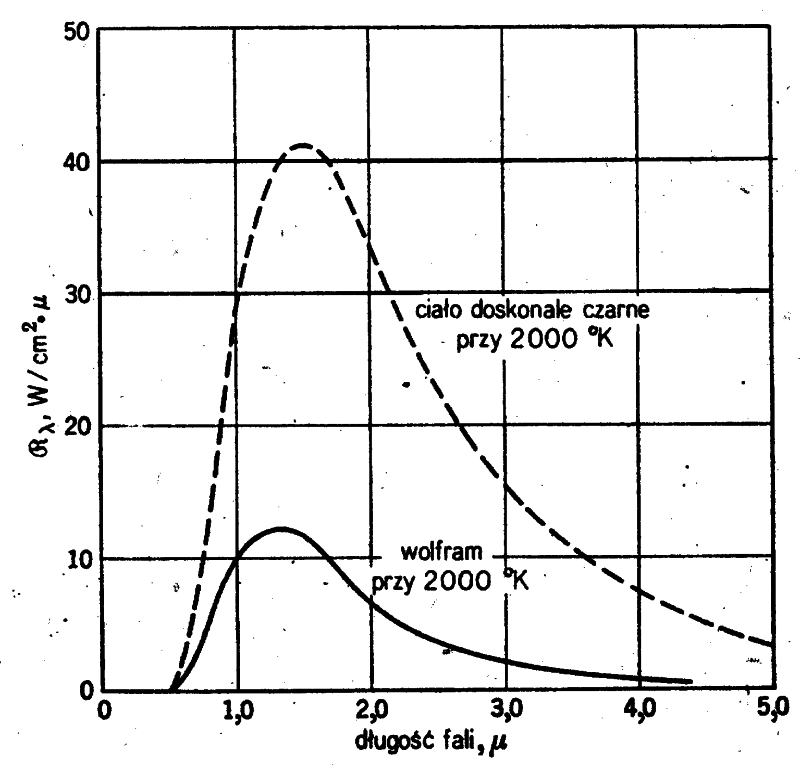
- nie zależy ani od rodzaju substancji ani od kształtu, a jedynie od temperatury ciała;

- widmo jest ciągłe;

- opisane jest dla ciała doskonale czarnego (ciała, którego powierzchnia absorbuje całe promieniowanie termiczne).

Emisja energetyczna promieniowania ciała doskonale czarnego zmienia się z temperaturą zgodnie z prawem Stefana-Boltzmana:

R = σ⋅T⁴ gdzie σ =

Zauważmy, że maksima natężenia promieniowania dla różnych temperatur przypadają na różne długości fal. Tzn. można to zapisać:

λ₁T₁ = λ₂T₂= λ₃T₃=…. Ogólnie λ⋅T = const - prawo Wiena

Zastosowanie: pomiar temperatury gwiazd na podstawie analizy widmowej. Mierzymy λ ⇒ λ⋅T = 2,898⋅10^-3 [m⋅K] i stąd obliczmy temperaturę gwiazdy.

Podejmowano różne próby oparte na fizyce klasycznej, wyjaśnienia rozkładu promieniowania ciała doskonale czarnego.

Teoria Wiena:
gdzie c₁, c₂ to stałe wyznaczane doświadczalnie. Pokrywała się ona z wynikami doświadczalnymi jedynie dla małych długości fal. Z kolei teoria Rayleigh'a była zgodna z doświadczeniem tylko dla dużych λ.

Dopiero Max Planck (1900) zmodyfikował wzór Wiena:

otrzymując pełną zgodność z wynikami doświadczalnymi.

Chcąc zbudować teorię wyjaśniającą otrzymaną zależność założył, że atomy ciała doskonale czarnego zachowują się jak oscylatory harmoniczne o charakterystycznych częstościach drgań:

1. Energia oscylatora jest kwantowana i dana wzorem: E = nhν gdzie n = 1, 2, 3… - liczba kwantowa, h = 6,63⋅10^-34 - stała Plancka.

2. Oscylatory nie wypromieniowują energii w sposób ciągły, ale kwantowany, tzn. wypromieniowana ilość energii ΔE = hν. Oscylator znajdujący się w stanie stacjonarnym (jeden ze stanów kwantowych) nie emituje ani ni absorbuje energii.

Planck wyznaczył wówczas na drodze teoretycznej stałe:
,
gdzie c - prędkość światła, k - stała Boltzmana. (1918 - nagroda Nobla)

Przykład:

Klasyczny oscylator o częstotliwości ν = 0,5 Hz i energii E = 0,1 J. Liczba kwantowa takiego oscylatora
(!) Jeżeli n zmienia się o jedność, to względna zmiana energii oscylatora
co jest praktycznie niemierzalne, czyli kwantowa natura drgań obiektów makroskopowych jest niewidoczna.

15.2. Zjawisko fotoelektryczne

Fotoelektrony wybijane z katody, przyspieszane przez pole elektryczne, tworzą prąd elektryczny, który płynie miedzy katodą a anodą nawet po przyłożeniu przeciwnego potencjału do anody. Natężenie prądu fotoelektrycznego spada do zera przy potencjale anody równym U_h - potencjał (napięcie) hamujące. E_kmax= e⋅ U_h

Na wykresie natężenia fotoprądu od przyłożonego napięcia, krzywą b otrzymano przy dwukrotnym zmniejszeniu natężenia światła.

Stosowane katody: Li, Cs, Rb

Wyjaśnienie zjawiska:

Planck: światło to fala elektromagnetyczna, rozchodząca się w postaci kwantów energii.

Jednakże wówczas, zgodnie z teorią falową:

1. energia kinetyczna fotoelektronów powinna wzrastać wraz z natężeniem światła,

2. efekt ten powinien występować dla dowolnej częstotliwości światła (o odpowiednio dużym natężeniu),

3. przy małym natężeniu światła, fotoelektrony powinny wykazywać opóźnienie wybicia w stosunku do czasu rozpoczęcia naświetlania, aby zmagazynować energię.

Tych efektów się nie obserwuje !!

Einstein: światło rozchodzi się w postaci cząsteczek - fotonów, z których każdy unosi kwant energii:

A zatem w zjawisku fotoelektrycznym spełniona jest zasada zachowania energii:

hν = W + E_k gdzie W - praca wyjścia elektronu, charakterystyczna dla danego metalu katody.

Jeżeli E_k = 0 to
jest to graniczna długość światła, przy której zachodzi zjawisko fotoelektryczne.

Z zasady zachowania energii:

Jest to więc sposób wyznaczenia pracy wyjścia

oraz wartości stałej Plancka.

U_h

ν

ν_o

ν

α

U_h

---