15. Zjawiska korpuskularno-falowe

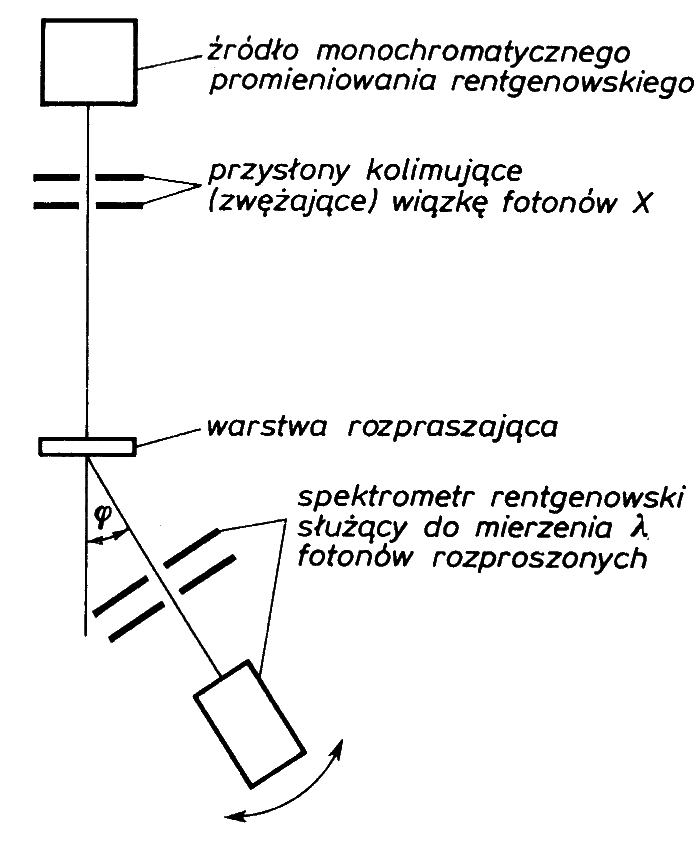
15.3. Zjawisko Comptona

Jest to drugi efekt wskazujący na korpuskularna naturę światła. Compton (1923) zaobserwował rozproszone promienie X o zmienionej długości fali. Klasyczna teoria fal elektromagnetycznych zjawisko rozproszenia tłumaczyła jako pobudzenie do drgań elektronów ośrodka rozpraszającego, które staja się wtórnym źródłem fal - ale bez zmiany długości !

Według teorii kwantowej zjawisko polega na zderzeniu padającego fotonu z elektronem swobodnym. Podczas zderzenia foton oddaje elektronowi jedynie część energii.

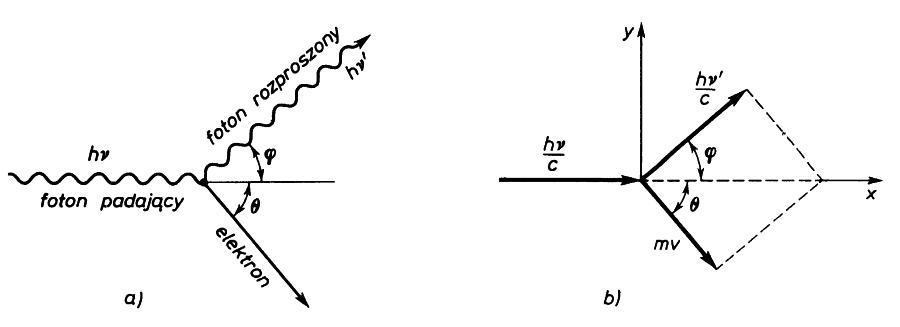
Zasada zachowania energii: Zasada zachowania pędu:

Zasada zachowania energii: Zasada zachowania pędu dla osi OX:

Zasada zachowania pędu dla osi OY:

Po wyeliminowaniu z równań v oraz ϕ otrzymujemy:

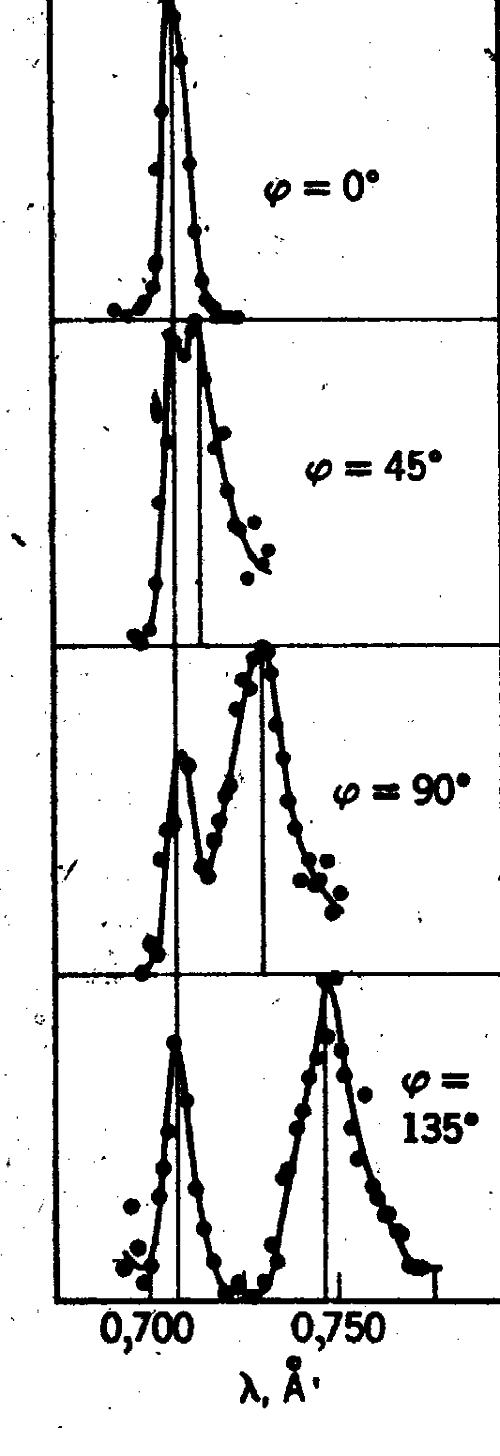
W zjawisku Cmptona zmiana długości fali nie zależy od energii fotonu padającego, a zależy jedynie od kata jego rozproszenia.

Dla ϕ = 0⁰ Δλ = 0; dla ϕ = 180⁰ Δλ = 2 Λ (rozproszenie wsteczne), a dla ၪ = 90⁰ ၄ၬ = Λ

Oba opisy światła: falowy i korpuskularny są poprawne: w pewnych przypadkach promieniowanie elektromagnetyczne zachowuje się jak fala o określonej długości i częstotliwości, a w innych jak zbiór fotonów o określonym pędzie i zerowej masie spoczynkowej. Przejście od obrazu falowego do korpuskularnego opisują wzory:

Dokładniej omówiony ten problem będzie w rozdz.16.

15.4. Model atomu Bohra

Postulaty Bohra:

I. Atom wodoru może znajdować się jedynie w ściśle określonych stanach stacjonarnych, w których nie promieniuje energii.

II. Elektron atomu w stanie stacjonarnym porusza się tylko po takich orbitach kołowych, dla których moment pędu jest skwantowany, tzn. spełnia zależność:
gdzie n = 1, 2, ..

III. Warunkiem wypromieniowania energii jest przejście atomu ze stanu o energii wyższej E_k do stanu o energii niższej E_j : hν = E_k - E_j

Skoro elektron porusza się po orbicie kołowej pod wpływem siły kulombowskiej będącej siłą dośrodkową, to z tego warunku można obliczyć prędkość elektronu. A zatem pęd p elektronu i jego moment pędu L można zapisać:

Uwzględniając warunek kwantyzacji momentu pędu otrzymujemy wyrażenia na promień orbity i energię kinetyczną elektronu.

A zatem promień orbity rośnie jak n², a energia całkowita rośnie (do zera) jak 1/n². Jonizacji atomu odpowiada n = ∝. Wówczas całkowita energia atomu E = 0, a r = ∝.

Energia atomu w stanie podstawowym n = 1 : E₁ = -13,6 eV

Na podstawie powyższych wzorów otrzymujemy wzór na częstość linii widmowych atomu wodoru:

gdzie R jest stałą Rydberga.

Przejścia elektronu miedzy kwantowanymi poziomami energetycznymi można przedstawić w postaci tzw. serii widmowych.

Linie serii zagęszczają się w kierunku fal krótkich, a każdą serię ogranicza linia odpowiadająca najmniejszej długości fali danej serii.

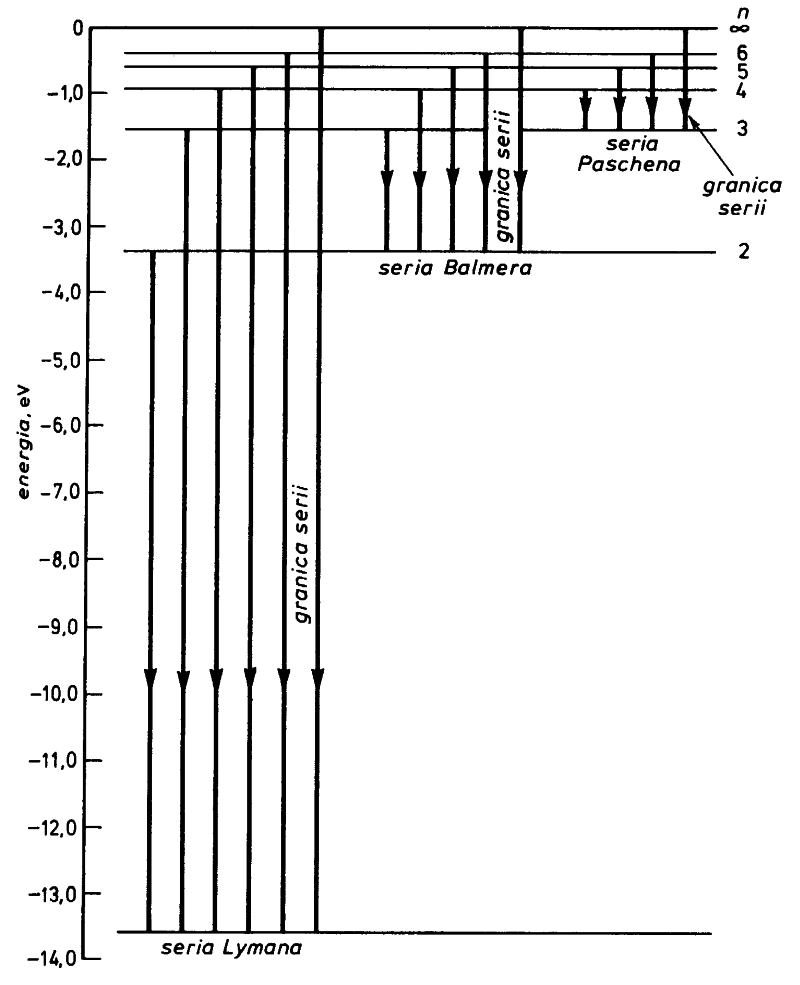
Przykład:

Obliczyć długość fali emitowanej przy przejściu elektronu z orbity 3 na pierwszą.

---