Politechnika Lubelska W Lublinie	Laboratorium Elektryczne
		Ćwiczenie nr 12
Anna Płaska Michał Wydra Andrzej Wasiuk	Semestr II	Grupa ED 2.6	Rok akademicki 1998
Temat ćwiczenia: Obwody magnetyczne sprzężone		Data wykonania: 1998.05.27	Ocena:

1. Teoria.

Indukcją własną nazywamy zmianę strumienia magnetycznego, skojarzonego z elementem indukcyjnym uwarunkowaną zmianą natężenia prądu w tym elemencie.

Indukcją wzajemną nazywamy zmianę strumienia magnetycznego skojarzonego z elementem indukcyjnym i uwarunkowaną zmianą natężenia prądu w innym elemencie indukcyjnym położonym w jego sąsiedztwie.

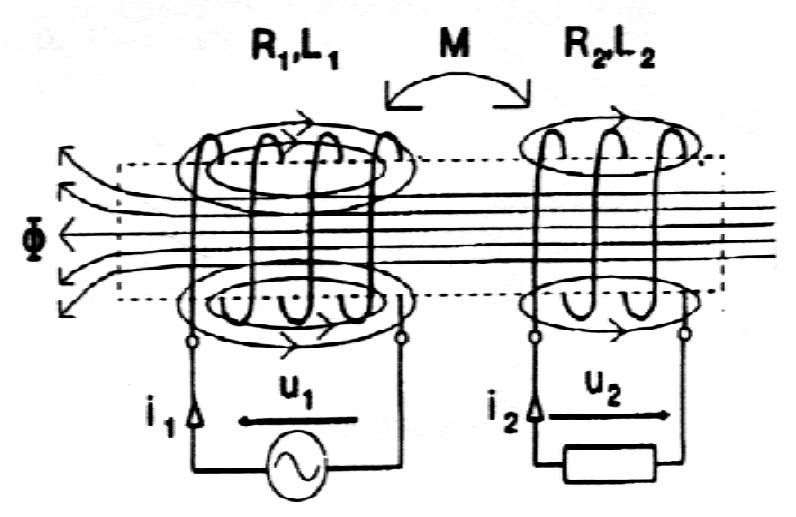
Obwody z elementami indukcyjnymi, w których indukuje się napięcie indukcji wzajemnej, noszą nazwę obwodów magnetycznie sprzężonych. Miarą oddziaływania pol magnetycznych jest współczynnik indukcyjności wzajemnej M.

M=k*sqrt(L1*L2)

k- współczynnik sprzężenia magnetycznego cewek.

Rodzaje sprzężeń:

• bardzo słabe 0<k<0.01

• słabe 0.01<k<0.05

• silne 0.05<k<0.9

• bardzo silne 0.9<k<1

Zmianę sprzężenia można osiągnąć przez zmianę położenia elementów względem siebie lub poprzez zastosowanie rdzenia. Tego rodzaju wzmocnienie sprzężenia jest stosowane w transformatorach i maszynach elektrycznych.

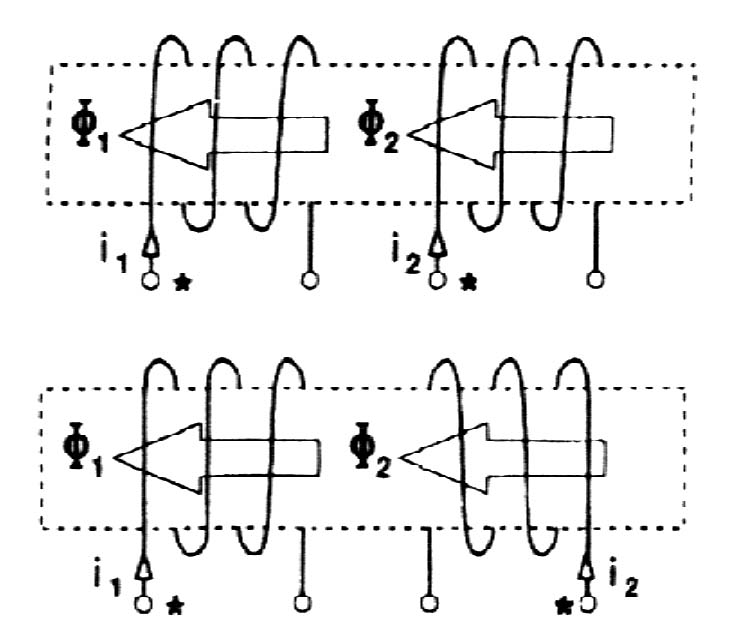
Napięcie sprzężenia dodaje się lub odejmuje od napięcia w oczku RL, zależnie od umownych zwrotów prądów przyjętych za dodatnie względem zacisków jednoimiennych.

1. zgodnie (dodatnio)

2. przeciwnie (ujemnie)

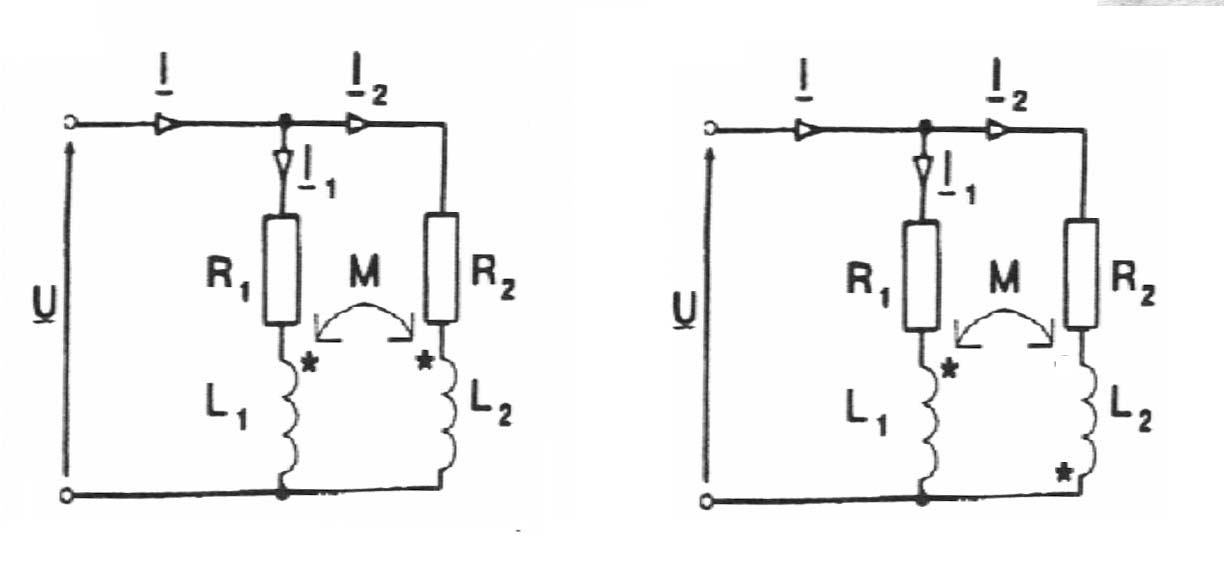
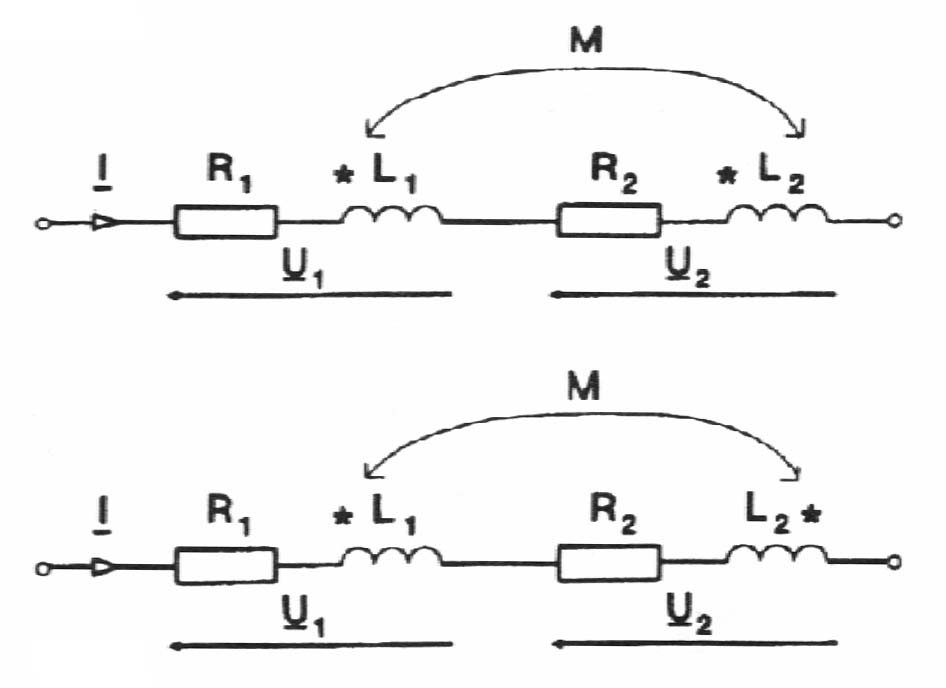
Połączenie szeregowe Połączenie równoległe

Transformator powietrzny

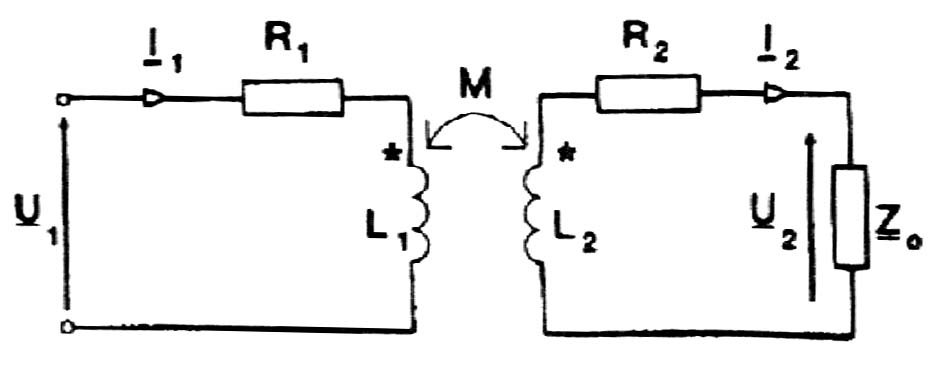
Transformatorem powietrznym (bezrdzeniowym) nazywamy układ dwóch cewek magnetycznie sprzężonych, nawiniętych na rdzeniu z materiału nieferromagnetycznego, nie połączonych ze sobą elektrycznie. Sprzężenie magnetyczne pomiędzy uzwojeniami transformatora tego typu nie jest zbyt dobre i przeważnie charakteryzuje się dużym rozproszeniem. Transformatory takie stosuje się w urządzeniach w.cz.

2. Wykonanie ćwiczenia.

1. Wyznaczanie parametrów pojedynczych cewek.

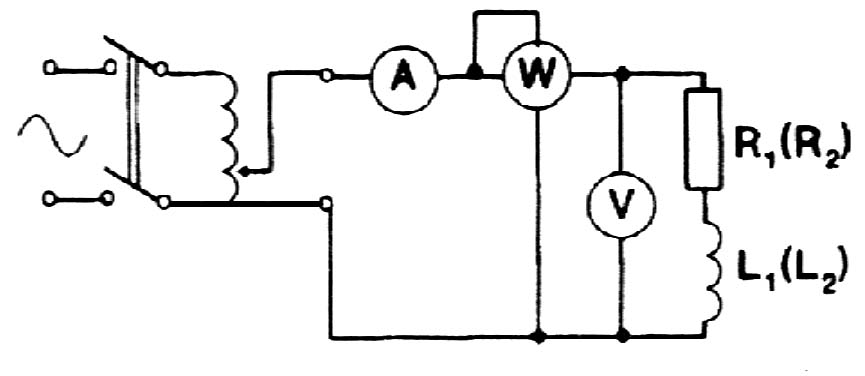
Do ćwiczenia użyliśmy woltomierza EP 43.3/135; amperomierza EP 43.3; watomierza EP 43.3/360 oraz cewek o L=0.62H i R=54Ω.

Pomiary przeprowadziliśmy dla obu cewek.

Cewka	Lp.	Pomiary			Obliczenia
		U	I	P	Z	R	XL	L
		V	A	W	Ω	Ω	Ω	H
1	1	50	0.247	5	202	55	194,77	0,62
	2	100	0.5	17	200	49	194,77	0,62
	3	150	0.75	38	200	49	194,77	0,62
2	1	50	0.25	4	200	49	194,77	0,62
	2	100	0.5	17	200	49	194,77	0,62
	3	150	0.75	38	200	49	194,77	0,62

R₁=54Ω L₁=0,62H R₂=54Ω L₂=0,62H

Przykładowe obliczenia:

X_L=2*π*f*L=2*3,14*50Hz*0.62H=194,77Ω

Z=U/I=50V/0.247A=202Ω

R=sqrt(Z²-X_L²)=sqrt(40804-37636)=55Ω

2. Połączenie szeregowe.

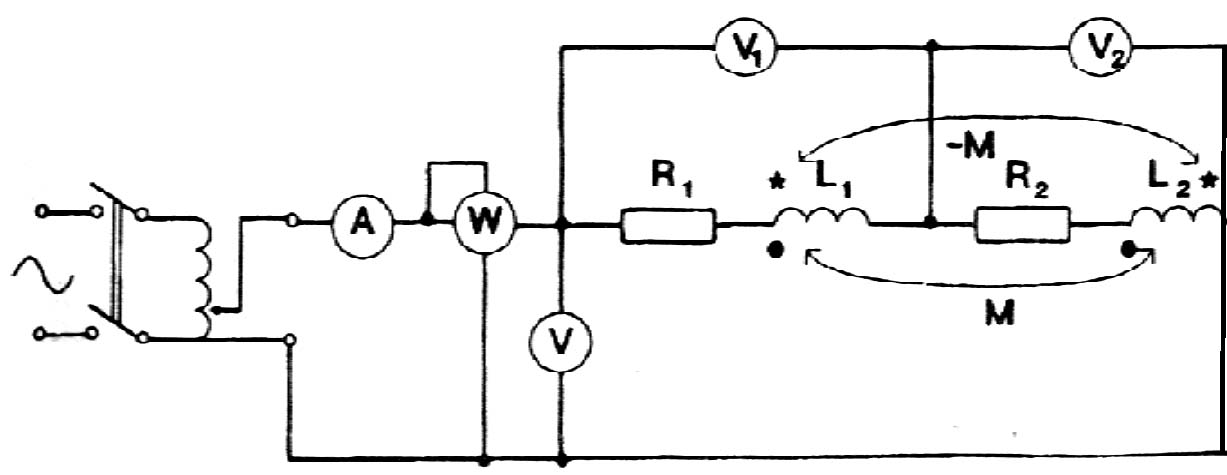
Do ćwiczenia użyliśmy woltomierzy EP 43.3/135, EP 43.3/326, EP 43.3/770; amperomierza EP 43.3; watomierza EP 43.3/360 oraz cewek o L=0.62H i R=54Ω. Pomiary przeprowadziliśmy dla obu cewek, połączonych zgodnie i przeciwnie.

Sprzężenie	Lp.	Pomiary						Obliczenia
		l	U	U1	U2	I	P	Z	cosϕ	X	M	k
		cm	V	V	V	A	W	Ω	---	Ω	H	---
+	1	0	100	48	50	0,18	7	555	0,38	544	0,27	0,435
	2	5	100	48	50	0,23	10	434	0,43	420	0,07	0,11
	3	10	100	48	50	0,25	11	400	0,44	385	0,02	0,03
	4	15	100	48	50	0,26	12	384	0,46	368	0,02	0,03
	5	19	100	50	50	0,26	12	384	0,46	368	0,02	0,03
-	1	0	100	48	50	0,53	33	188,6	0,62	153	0,27	0,435
	2	5	100	48	50	0,32	15	344	0,468	326	0,07	0,11
	3	10	100	48	50	0,29	13	370	0,44	353	0,02	0,03
	4	15	100	50	50	0,28	12	357	0,42	340	0,02	0,03
	5	19	100	50	50	0,28	12	357	0,42	340	0,02	0,03

Przykładowe obliczenia:

Z=U/I=100V/0.18A=555Ω

cosϕ=P/(U*I)=7W/(100V*0,18A)=0,38

X=sqrt(Z²-2*R²)=sqrt(308025-11664)=544Ω

M=(Z_Z²-Z_P²)/(8ω²(L₁+L₂))=(308025-355689.96)/(8*(2*3.14*50Hz)²*(1,24H))=0.27H

k=M/sqrt(L₁*L₂)=0.27/0.62=0,435

Bilans napięć dla pomiaru 1:

ϕ=arccos 0,38=67`

I=I*e-^j0=I=0,18A

U=U₁+U₂=[R₁+R₂+jω(L₁+L₂+2M]*I

U=[54Ω+54Ω+j(2*3.14*50Hz)*(0,62H+0,62H+2*0,27H)]*0,18A=19,44+j100

U=sqrt(19,44²+100²)V=101V

ϕ=arccos 0,62=51,7`

I=I*e^j0=I=0,53A

U=U₁+U₂=[R₁+R₂+jω(L₁+L₂-2M]*I

U=[54Ω+54Ω+j(2*3.14*50Hz)*(0,62H+0,62H-2*0,27H)]*0,53A=57,24V+j109

U=sqrt(57,24²+109²)V=123,3V

Wykresy wektorowe dla prądu i napięć:

1. Dla elementów połączonych szeregowo zgodnie b) Dla elementów połączonych szeregowo przeciwnie

Wykresy X=f(l); M=f(l); k=f(l);

3. Połączenie równoległe.

Do ćwiczenia użyliśmy woltomierza EP 43.3/135; amperomierzy EP 43.3, EP 43.3/301, EP 43.3/1683; watomierza EP 43.3/360 oraz cewek o L=0.62H i R=54Ω. Pomiary przeprowadziliśmy dla obu cewek, połączonych zgodnie i przeciwnie.

Sprzężenie	Lp.	Pomiary						Obliczenia
		l	I	I1	I2	U	P	Z	R	X
		cm	A	A	A	V	W	Ω	Ω	Ω
+	1	0	0,66	0,35	0,32	100	15	151	34.32	146.47
	2	5	0,86	0,44	0,42	100	24	116	32.37	111.36
	3	10	0,92	0,48	0,46	100	29	108	34.04	102.49
	4	15	0,96	0,5	0,48	100	30	104	32.50	98.70
	5	19	0,96	0,5	0,49	100	30	104	32.50	98.80
-	1	0	2	1,4	1	100	120	50	30.00	40.00
	2	5	1,2	0,62	0,6	100	44	83	30.43	77.19
	3	10	1,06	0,56	0,52	100	36	94	31.92	88.36
	4	15	1,02	0,53	0,5	100	34	98	32.67	92.32
	5	19	1	0,51	0,5	100	34	100	34.00	94.00

Przykładowe obliczenia: Z=U/I=100V/0,66A=151Ω; R=Z*cosφ=Z*(P/(U*I)=151Ω*0.227=34.32Ω; X=Z*sinφ=151*0.97=146.47Ω

Wykres wektorowy dla pomiaru 2 (zgodnie i przeciwnie)

4. Pomiar przekładni napięciowej w stanie jałowym oraz wyznaczanie indukcyjności wzajemnej cewek w zależności od odległości.

Do ćwiczenia użyliśmy woltomierzy EP 43.3/135, EP 43.3/326; amperomierza EP 43.3 oraz cewek o L=0.62H i R=54Ω.

U1=250V U1=150V

Lp.		Wart. zmierzona		Wart. obliczona			Wart. zmierzona		Wart. obliczona
	Odl.	U2	I	ϑu	M.	k	U2	I	ϑu	M	k
	cm	V	A	--	H	---	V	A	---	H	--
1	0	134	1.25	1.9	0.341	0.55	80	0.76	1.9	0.20	0.33
2	1	106	1.25	2.4	0.270	0.44	64	0.76	2.3	0.16	0.26
3	2	84	1.25	3	0.214	0.35	50	0.76	3	0.13	0.21
4	3	66	1.25	3.8	0.168	0.27	40	0.76	3.8	0.10	0.16
5	4	52	1.25	4.8	0.132	0.21	31	0.76	4.8	0.08	0.13
6	5	44	1.25	5.7	0.112	0.18	26	0.76	5.8	0.07	0.11
7	6	36	1.25	6.9	0.092	0.15	22	0.76	6.8	0.06	0.09
8	7	29	1.25	8.6	0.074	0.12	16	0.76	9.4	0.04	0.07
9	8	24	1.25	10	0.061	0.10	14	0.76	11	0.04	0.06
10	9	20	1.25	13	0.051	0.08	12	0.76	13	0.03	0.05
11	10	16	1.25	16	0.041	0.07	10	0.76	15	0.03	0.04
12	11	14	1.25	18	0.036	0.06	8	0.76	18	0.02	0.03
13	12	10	1.25	25	0.025	0.04	6	0.76	25	0.02	0.02

Przykładowe obliczenia:

ϑu=U₁/U₂=250V/134V=1.9

M=U₂/(ωI₁)=134V/(2*3.14*50Hz*1,25A)=0,341

k=M/sqrt(L₁*L₂)=0.341/0.62=0,55

Wykresy charakterystyk ϑu=f(l), k=f(l) dla różnych napięć U1.

5. Obciążenie transformatora

Do ćwiczenia użyliśmy woltomierzy EP 43.3/135, EP 43.3/326; amperomierzy EP 43.3, EP 3.3/301 watomierza EP 43.3/360 oraz cewek o L=0.62H i R=54Ω i
rezystora Ro=160Ω

U1=const

Lp.	Pomiary					Obliczenia
	U1	U2	I1	I2	P	ϑu	Ro	Zwe	Rwe	Xwe
	V	V	I	I	W	---	Ω	Ω	Ω	Ω
1	150	48	0,82	0,3	67	3.1	160	182.9	82,47	168,85
2	150	42	0,86	0,35	72	3.6	120	174.4	82,76	162,58
3	150	31	0,91	0,4	76	4.8	77.5	164.83	79,40	157,14
4	150	24	0,92	0,45	80	6.3	53	163	79,59	148,18

Przykładowe obliczenia:

Ro=U2/I2=48V/0,3A=160Ω;

M=(sqrt[(R₂+R_o)²+(ω*L₂)]*I₂)/ (ω*I₁) = 0,336H

Zwe=U₁/I₁=150V/0,82A=182,9Ω

R_we=R₁+[[(ω*M)²*(R₂+R_o)]/ [(R₂+R_o)²+(ω*L₂)²]]= =54Ω+[[(2*3.14*50Hz*0,336H)²*(54Ω+160Ω)]/[(54Ω+160Ω)²+(2*3.14*50Hz*0,62H)²=82,47Ω

X_we=ω[L₁-[(ω*M)²*L₂]/[(R₂+R_o)²+(ω*L₂)²]]= 2*3.14*50Hz*[0,62H-

-(2*3.14*50Hz*0,336H)²*0,62H]/[(54Ω+160Ω)²+(2*3.14*50Hz*0,62H)²]]=168,85Ω

Z praw Kirchoffa wyznaczamy wykresy wektorowe dla pomiaru 1:

U₁=(R₁+jωL₁)*I₁-jωM*I₂

0=(R₂+R₀+jωL₂)*I₂-jωM.*I₁

Wykres wektorowy dla pomiaru pierwszego:

Wykresy zależności U_o=f(Ro); I₁=f(Ro); I₂=f(Ro); P=f(Ro);

Wnioski:

Ad2. Połączenie szeregowe.

Z przeprowadzonych pomiarów wynika, że przy połączeniu zgodnym cewek sprzężonych magnetycznie wraz ze zwiększaniem odległości, zmniejsza się impedancja oraz reaktancja obwodu, maleje kąt przesunięcia fazowego między prądem i napięciem. Zmniejsza się też współczynnik sprzężenia M oraz k. Spowodowane jest to zmniejszeniem oddziaływania jednej cewki na drugą. Moc rośnie wraz ze zwiększeniem odległości. Rośnie też prąd. Jest to spowodowane zmniejszającą się impedancją Z, na którą wpływ ma X_M (reaktancja sprzężenia). Przy połączeniu przeciwnym, wraz ze wzrostem odległości rośnie impedancja i reaktancja , rośnie kąt przesunięcia fazowego. Maleje moc, maleje prąd. Przy połączeniu przeciwnym jest to konsekwencją zwiększenia impedancji wypadkowej. Przy połączeniu zgodnym napięcie sprzężenia dodaje się do napięcia na cewkach, przy połączeniu przeciwnym, odejmuje się. Jest to zgodne z teorią.

Ad3. Połączenie równoległe.

Przy połączeniu równoległym zgodnym, wraz ze wzrostem odległości maleje impedancja oraz reaktancja, stała jest rezystancja R. Rosną prądy w gałęziach, rośnie też moc. Jest to spowodowane wpływem reaktancji sprzężenia X_M . Przy połączeniu przeciwnym, wraz ze wzrostem odległości rośnie impedancja, reaktancja. Zmniejsza się moc oraz prąd w gałęziach. Tu także jest to spowodowane wpływem reaktancji sprzężenia X_M .

Na wykresach wektorowych widać, że przy połączeniu zgodnym, sprzężenie zmniejsza wartość prądu, przy połączeniu przeciwnym zwiększa. To także zgodne jest z teorią

Ad4. Przekładnia napięciowa w stanie jałowym.

Z pomiarów widać, że wraz ze wzrostem odległości rośnie przekładnia transformatora, maleją odpowiednio M oraz k. Widać też że przekładnia nie zależy od napięcia na uzwojeniu wtórnym, dla 250 i 150 V obliczone wartości przekładni transformatora są takie same. Różne są natomiast wartości wsp. sprzężenia M i k.

Ad5. Obciążenie transformatora.

Przy obciążeniu transformatora zauważyć można że wraz ze zmianą obciążenia zmieniają się zarówno prąd w obwodzie pierwotnym jak i we wtórnym. Dodatkowo zmienia się moc w obwodzie pierwotnym oraz napięcie w obwodzie wtórnym. Wraz ze zmniejszeniem obciążenia Ro rośnie przekładnia transformatora, maleje natomiast impedancja wejściowa Zwe oraz rezystancja wejściowa Rwe oraz związana z nimi reaktancja wejściowa Xwe transformatora. To właśnie jest przyczyną zmiany prądu oraz w konsekwencji mocy w obwodzie pierwotnym.

I

U_R1

U₁

U_L1

U_R2

U₂

U_M1

U_L2

U_M2

U

Skala napięć 1:10

Skala prądów 10:1

I

U_R1

U₁

U_L1

U_R2

U₂

U_M1

U_L2

U_M2

U

U_R/R₁

I₂

U

U/jωL₁I₁

U/jωMI₁

I₁

U/R₂

I

U/jωMI₂

U

U/R₁

U/jωL₁I₁

U/jωMI₁

I₁

U/R₂

I₂

I

U/jωL₂I₂

U/jωL₂I₂

U/jωMI₂

jωMI₁

U₁

-jωMI₂

jωL₁I₁

jωL₂I₂

R₁*I₁

I₁

R₂*I₂

R_o*I₂

I₂

---