WOJSKOWA AKADEMIA TECHNICZNA

Wydział Inżynierii Lądowej i Geodezji

Katedra Budownictwa

Instrukcja do zajęć laboratoryjnych z przedmiotu:

Wytrzymałość Materiałów

Ćwiczenie nr 2

Temat ćwiczenia :

Wyznaczenie stałych materiałowych metali przy osiowym rozciąganiu

za pomocą tensometrów elektrooporowych.

1. Cel ćwiczenia

Celem ćwiczenia jest :

• Zapoznanie się z tensometrią elektrooporową i różnymi rodzajami tensometrów.

• Zapoznanie z obsługą mostka tensometrycznego KWS 106D.

• Wyznaczenie współczynnika sprężystości podłużnej (wzdłużnej) - modułu Younga.

• Wyznaczenie liczby Poissona i modułu odkształcenia postaciowego.

2. Wprowadzenie

2.1 Naprężenia w pręcie osiowo rozciąganym

Naprężenia można wyznaczyć bezpośrednio z definicji

[1]

gdzie: σ - naprężenie normalne,

F - siła,

S - pole przekroju poprzecznego,

jedynie w najprostszych przypadkach, jakim jest pręt o stałym przekroju obciążony siłą osiową przyłożoną w środku ciężkości przekroju poprzecznego.

W wielu przypadkach naprężenia można wyliczyć ze wzorów wytrzymałościowych, które opierają się na pewnych upraszczających założeniach, nieuwzględniajacych spiętrzeń naprężeń związanych ze zmianami przekrojów.

Jednym z działów doświadczalnej analizy naprężeń jest tensometria. Inne ważne metody tej analizy to metody holograficzne, mory, rentgenowskie, elastooptyczne i kruchych pokryć.

Tensometria zajmuje się pomiarami odkształceń konstrukcji. Ponieważ naprężenia w zakresie sprężystości są związane z odkształceniami względnymi ε prostymi, liniowymi związkami (uogólnionym prawem Hooke'a)

[2]

gdzie: x, y, z - trzy dowolne wzajemnie ortogonalne kierunki,

E - moduł Younga,

ν - współczynnik Poissona,

można uważać tensometrię za doświadczalną metodę wyznaczania stanu naprężenia.

W przypadku jednoosiowego stanu naprężenia prawo Hooke'a ma postać:

[3]

Odkształcenie względne jest zdefiniowane jako

[4]

gdzie
jest odkształceniem bezwzględnym odcinka o długości początkowej l_{0 .}

Z powyższych dwóch wzorów wynika, że aby wyznaczyć naprężenia w jedno­osiowym stanie naprężenia, wystarczy zmierzyć
pewnego odcinka równoległego do kierunku naprężeń σ. Na tej zasadzie działa większość różnego typu tensometrów. Ważny wyjątek stanowią tensometry rezystancyjne, których wskazania są bezpośrednio powiązane z odkształceniem względnym.

2.2. Podział tensometrów elektrycznych

W grupie tensometrów elektrycznych wyróżnić można następujące zasadnicze typy:

• rezystancyjne,

• indukcyjne,

• pojemnościowe,

• piezoelektryczne,

• elektrodynamiczne.

Obecnie najczęściej są stosowane tensometry rezystancyjne (elektrooporowe). Wykorzystuje się w nich zmianę rezystancji przewodnika w wyniku jego odkształceń. Ze względu na ich znaczenie i odmienną budowę zostaną one szczegółowiej omówione w następnym punkcie.

Drugą pod względem rozpowszechnienia grupą tensometrów elektrycznych są tensometry indukcyjne. Mają one budowę podobną do tensometrów mechanicz­nych, to znaczy: dwa ostrza wyznaczają bazę tensometru, odkształcenia bazy po­wodują obrót (ewentualnie równoległe przemieszczenie) organu ruchomego. Róż­nica polega na tym, że położenia organu ruchomego nie odczytuje się ze skali, lecz w zależności od typu tensometru mierzy się zmianę indukcyjności, spowodowaną zmianą położenia zwory i rdzenia cewki lub zmianą położenia rdzenia w cewce. Czujniki indukcyjne są zbudowane najczęściej z dwu cewek połączonych w układ półmostka Wheatstone'a.

Zaletą tensometrów indukcyjnych jest między innymi to, że pomiary wykonuje się za pomocą szeroko rozpowszechnionej aparatury pomiarowej stosowanej w tensometrii rezystancyjnej. Druga ich zaleta polega na tym, że w wyniku stosun­kowo małych zmian konstrukcyjnych można zbudować czujniki współpracujące z tą samą aparaturą, a przeznaczone do pomiaru przemieszczeń zarówno rzędu mi­krometrów, jak i metrów. Czujniki indukcyjne o małym zakresie pomiarowym przeznaczone do pomiaru odkształceń nazywamy przeważnie tensometrami induk­cyjnymi, natomiast o większych zakresach — indukcyjnymi przetwornikami prze­mieszczenia .

Możliwość rejestracji sygnału pomiarowego umożliwia prowadzenie za pomocą tych tensometrów pomiarów odkształceń zmiennych, jednak stosunkowo duże masy elementów ruchomych silnie ograniczają maksymalną częstotliwość zmian mierzonych odkształceń.

Tensometry pojemnościowe, piezoelektryczne i elektrodynamiczne mogą być budowane na podobnej zasadzie jak powyżej opisane, z tym że tutaj element po­miarowy stanowi kondensator, kryształ wykazujący własności piezoelektryczne lub uzwojenie, w którym w wyniku ruchu magnesu indukuje się siła elektrodynamicz­na. Głównym przeznaczeniem tych czujników są pomiary dynamiczne, co zmusza do zastosowania bardziej zwartej budowy. Najczęściej są one wykorzystywane nie do pomiaru odkształceń powierzchni, ale do pomiarów przemieszczeń prostopa­dłych do powierzchni - do pomiarów amplitudy, prędkości i przyspieszenia drga­jących konstrukcji.

2.3.Tensometry rezystancyjne

Budowę tensometru rezystancyjnego przedstawiono na rys.1 i 2. Jest on zbudowany z przewodnika 1 lub półprzewodnika przyklejonego specjalnym klejem 2 do podkładki nośnej 3, wykonanej z papieru, celuloidu, a obecnie najczęściej z folii z two­rzywa sztucznego. Od góry jest zabezpieczony nakładką ochronną 4. Do końców elementu rezystancyjnego najczęściej są przylutowane druciki 5 służące do łącze­nia tensometru z przewodami układu pomiarowego.

Rys.1 Tensometry rezystancyjne a) wężykowy, b) kratowy, c) foliowy, d) półprzewodnikowy, e) przekrój wzdłużny tensometru foliowego.

W zależności od sposobu wykonania i zastosowanego materiału rozróżnia się tensometry wężykowe, kratowe, foliowe i półprzewodnikowe (rys. 1). Trzy pierwsze typy wykonuje się z materiałów przewodzących, takich jak: konstantan, nichrom, kanthal. W dwu pierwszych typach elementem rezystancyjnym jest dru­cik o średnicy od 10 do 50 μm, w tensometrach foliowych element rezystancyjny jest wykonany z folii metalowej o grubości od kilku do kilkunastu mikrometrów.

W tensometrze wężykowym przeważająca część drucika w kształcie wężyka jest ułożona w kierunku osi wzdłużnej tensometru na długości l₀ wyznaczającej bazę tensometru. Część drucika leży jednak poprzecznie do kierunku bazy (na łu­kach), co powoduje, że tensometry wężykowe są w pewnym stopniu czułe na od­kształcenia poprzeczne, a nie tylko na odkształcenia wzdłuż osi tensometru. Wady tej nie mają tensometry kratowe ani foliowe.

Tensometr kratowy (rys. 1b) jest wykonany z drucików ułożonych równole­gle i połączonych poprzecznymi odcinkami taśmy miedzianej w ten sposób, że poszczególne odcinki drucików rezystancyjnych są połączone szeregowo w jeden obwód. Łączenie drucików taśmą miedzianą o małej rezystywności i stosunkowo dużym przekroju poprzecznym, a więc o małej rezystancji, ma na celu wyelimino­wanie wpływu odkształceń poprzecznych na zmianę rezystancji tensometru. Z tego samego względu w tensometrach foliowych odcinki folii ułożone poprzecznie do kierunku bazy tensometru mają większą szerokość.

Rys. 2 Tensometr rezystancyjny - zasada działania.

Pierwszymi skonstruowanymi tensometrami były tensometry wężykowe. Obec­nie znajdują one jeszcze czasami zastosowanie w długotrwałych pomiarach od­kształceń zmiennych ze względu na ich większą w porównaniu z innymi tensome­trami wytrzymałość zmęczeniową.

Najnowocześniejsze są tensometry foliowe (rys. 3). Sposób ich wykonania umożliwia dowolne, optymalne dla danego zastosowania, kształtowanie układu elementu rezystancyjnego. Mają one również wiele innych zalet. Ze względu na to, że element rezystancyjny tensometru foliowego ma pro­stokątny przekrój poprzeczny, lepiej (w porównaniu z tensometrami drucikowymi) przejmuje odkształcenia podłoża. Lepiej również odprowadza do podłoża ciepło wydzielane w nim w czasie przepływu prądu, co pozwala stosować wyższe napię­cie prądu zasilania układu pomiarowego.

Rys. 3 Tensometry rezystancyjne foliowe.

Tensometry rezystancyjne są przeważnie tensometrami o średnich bazach (5 do 20 mm). Do pomiaru odkształceń materiałów o dużej niejednorodności (beton) stosuje się tensometry o dużych bazach (do 100 mm). Tensometry o małych i bar­dzo małych bazach (0,4 mm) stosuje się do pomiaru odkształceń małych przedmio­tów oraz w miejscach koncentracji naprężeń. Tensometry o małych bazach są wy­konywane tylko z folii.

2.4. Zasada działania tensometrów rezystancyjnych.

Tensometry przykleja się do powierzchni badanej konstrukcji tak aby jego oś symetrii pokrywała się z osią działania siły (rys. 2). Ze względu na bardzo mały przekrój poprzeczny, a więc i znikomą sztywność, druciki tensometru podle­gają tym samym odkształceniom co podłoże, na które tensometr został naklejony. Miejsce naklejenia musi być dokładnie oczyszczone zarówno mechanicznie jak i chemicznie.

Zasada działania tensometru rezystancyjnego opiera się na zależności rezystan­cji R od długości l, pola przekroju drutu S oraz rezystywności (oporu elektrycznego właściwego) ρ:

[5]

Jak wynika z powyższego wzoru rezystancja drutu oporowego tensometru wzrasta pod wpływem działania siły rozciągającej.

Po zlogarytmowaniu powyższego równania, zróżniczkowaniu i dalej przejściu na przyrosty skończone otrzymujemy zależność:

[6]

W drucikach tensometru panuje jednoosiowy stan naprężeń, więc

[7]

a zmiana pola przekroju poprzecznego w wyniku zmiany wymiarów poprzecznych zgodnie ze współczynnikiem Poissona jest postaci

[8]

Względna zmiana rezystywności dla materiałów o liniowej charakterystyce

[9]

gdzie C - stała.

Z powyższego wynika wzór opisujący pracę tensometru rezystancyjnego:

[10]

gdzie

[11]

co oznacza, że względna zmiana rezystancji tensometru jest proporcjonalna do odkształcenia względnego ε. Współczynnikiem proporcjonalności jest stała K, zwana stałą tensometru lub czułością tensometru.

Stała tensometrów wężykowych i kratowych zależy od rodzaju materiału oporowego zaś jej wartość waha się w granicach od 1,6 do 3,6. Dla tensometrów półprzewodnikowych wynosi około 100. Dużo wyższa czułość jest ich zaletą, a ich wadą jest duża czułość na zmiany czynników zewnętrznych (temperatury, ciśnienia).

2.5. Pomiary zmian rezystancji.

Ze wzoru opisującego pracę tensometru rezystancyjnego wynika, że jeśli znana jest stała tensometru oraz zmierzona zmiana rezystancji, można obliczyć odkształ­cenie względne. Używając tensometru o stałej K ≈ 2 i rezystancji R = 350Ω, celu zmierzenia odkształceń względnych rzędu 10^-6 należy wy­konać pomiar zmiany rezystancji ΔR rzędu 10^-4 Ω.

Pomiary tak małych rezystancji umożliwia układ pomiarowy zwany mostkiem Wheatstone'a z aparaturą wzmacniającą (rys.4, 5).

Rys.4 Zasada pomiaru zmian rezystancji tensometrów za pomocą mostka Wheatstone'a

Rys.5 Aparatura pomiarowa stosowana w tensometrii oporowej

Cztery rezystory (tensometry) R₁, R₂, R₃, R₄ włącza się w cztery gałęzie mostka. Mostek zasila się przemiennym lub stałym napięciem U przyłożonym do jednej przekątnej. Na drugiej przekątnej powstaje wówczas różnica napięć ΔU , która następnie jest wzmacniana i przesyłana do urządzenia pomiarowego lub rejestrującego.

Przy dużej impedancji wejściowej wzmacniacza możemy zapisać:

[12]

Mostek jest zrównoważony, gdy na przekątnej pomiarowej ΔU=0,a więc gdy

[13]

W przypadku gdy R₁= R₂ i R₃ = R₄ , dla małych zmian rezystancji ΔR_i zależność [8] można doprowadzić do postaci:

[14]

Podstawowy układ pomiarowy składa się z dwóch tensometrów o równej rezy­stancji (R₁= R₂ ), podłączonych do sąsiednich gałęzi mostka. Rezystancje R₃ i R₄ stanowią rezystory znajdujące się w tensometrycznej aparaturze wzmacniającej. Jeden z tensometrów - czynny - jest naklejony na powierzchnię konstrukcji w punkcie, w którym chcemy zmierzyć odkształcenia; drugi - na powierzchnię w miejscu, gdzie nie występują odkształcenia. Zmiana rezystancji w czasie pomiaru zachodzi tylko w jednej z czterech gałęzi mostka - w tej, do której podłączony jest tensometr czynny - i dlatego układ ten nazywa się układem ćwierćmostkowym. Ponieważ wtedy ΔR₂ = ΔR₃ = ΔR₄ = 0, przeto

[15]

A po uwzględnieniu wzoru [6], opisującego zasadę pracy tensometru rezystancyjnego, mamy:

[16]

Powyższe równanie jest podstawowym w tensometrii oporowej.

3 Aparatura pomiarowa.

W pierwszych aparatach pomiarowych stosowano metodę zerową. W tego typu aparaturze nie jest wymagany wzmacniacz wysokiej klasy. Wystarczy dobrej klasy potencjometr i wskaźnik zrównoważenia mostka.

Wraz z rozwojem elektroniki coraz popularniejsza stawała się aparatura pracu­jąca metodą, wychyłową, wymagającą wzmacniacza dobrej klasy o liniowej charak­terystyce wzmocnienia. Podstawowe bloki funkcjonalne tego typu aparatury to moduły: zasilania, równoważenia mostka, opracowania sygnału wyjściowego (pro­stowanie, wzmocnienie, filtrowanie, kalibracja). Obecnie na rynku dominuje apara­tura tego typu (rys. 5, 6).

Rys. 6. Podstawowe elementy kanału pomiarowego mostka KWS 106 D; 1- przełączniki regulacji wzmocnienia (zgrubny i dokładny), 2 - pokrętło przełączane równoważenia zgrubnego mostka pomiarowego, 3 - pokrętło płynnego równoważenia precyzyjnego, 4- przełącznik napięcia zasilania mostka ( 1, 5 i 10V) oraz przełącznik zmiany rodzaju mostka (półmostek lub pełny mostek tensometryczny).

Tensometry mogą być zasilane prądem stałym lub przemiennym. Bardziej roz­powszechniona jest aparatura z zasilaniem prądem przemiennym (od 225 Hz w aparaturze do pomiarów statycznych do 40 kHz w aparaturze dynamicznej). Napię­cie zasilania najczęściej jest z przedziału l do 5 V (wyższe napięcia przy pomia­rach na metalach, niższe na tworzywach sztucznych ze względu na gorsze odpro­wadzanie ciepła wydzielanego w tensometrze podczas pomiaru).

Do pomiarów dynamicznych buduje się najczęściej aparaturę wielokanałową (4- lub 6-kanałową z możliwością łączenia w większe zespoły). Aparatura statycz­na jest przeważnie 1-kanałowa ze skrzynką rozdzielczą (multiplekserem).

W uniwersalnej aparaturze pomiarowej wszystkie pokrętła i przełączniki znaj­dują się na frontowej ścianie aparatury, jest tam też analogowy lub cyfrowy wskaźnik mierzonych wielkości. W aparaturze do pomiarów dynamicznych każdy kanał ma wyjście napięciowe i prądowe służące do podłączania aparatury rejestru­jącej.

W wydaniu przemysłowym wszelkie urządzenia sterujące znajdują się we­wnątrz wodoszczelnej i pyłoszczelnej obudowy i są dostępne do regulacji jedynie za pomocą śrubokręta. Miniaturyzacja posunięta jest do tego stopnia, że wszystkie bloki funkcyjne aparatury mogą się znajdować na jednej małej płytce z obwodami drukowanymi, mieszczącej się w obudowie przetwornika.

Najnowocześniejsza tensometryczna aparatura pomiarowa często nie ma żad­nych pokręteł ani wskaźników. Jest całkowicie sterowana za pomocą komputera i do komputera przesyła wyniki pomiarów celu ich obróbki, wizualizacji i archiwi­zacji. Ważnym elementem tej aparatury jest przetwornik analogowo--cyfrowy.

Typowa uniwersalna tensometryczna aparatura pomiarowa z wyjściem analo­gowym była klasy 1. Nowoczesna uniwersalna aparatura z przetwornikiem A/C jest co najmniej klasy 0,1. Do zadań specjalnych budowana jest aparatura klasy 0,001 i lepszej.

4. Doświadczalne wyznaczenie stałych materiałowych przy osiowym rozciąganiu.

4.1 Próbki:

Do badań użyta będzie nie obrobiona próbka płaska o przekroju prostokąta i długość wynoszącej L = 400 mm wykonana ze stali. Na dwie przeciwległe płaszczyzny próbki naklejono dwa czujniki (nr 1 i 2) równoległe do kierunku rozciągania i dwa (nr 3 i 4) w kierunku poprzecznym. Czujniki kompensacyjne naklejono na takim samym materiale i umieszczono poza maszyną wytrzymałościową. Wszystkie użyte czujniki są tego samego typu i maja rezystancję zbliżoną do 350 Ω. Aparatura pomiarowa działa na zasadzie mostka Wheatstone'a. Odczyty będą realizowane metodą wychyłową.

Rys.7 Próbka pomiarowa z naklejonymi tensometrami w szczękach maszyny wytrzymałościowej; 1- płaskownik stalowy, 2 - tensometry foliowe ( T1 i 2 pionowy, T3 i 4 poziomy), 3 - kable połączeniowe z mostkiem tensometrycznym

4.2 Aparatura:

• uniwersalna maszyna wytrzymałościowa z mechanicznym urządzeniem obciążającym sterowanym silnikiem elektrycznym i ręcznie, o zakresie do 100 kN, elementarnej działce siłomierza 10 N;

• tensometry elektrooporowe o długości 10 - 30 mm

• mostek tensometryczny KWS 106 D.

4.3 Przebieg próby:

1. Przygotowanie maszyny wytrzymałościowej (ustawienie zakresu, zerowanie siłomierza itd.).

2. Pomiar próbki (szerokość, grubość).

3. Zamocowanie tensometrów na próbce (naklejenie).

4. Zamocowanie próbki w szczekach

5. Przylutowanie przewodów tensometrów czynnych i kompensacyjnych do odpowiednich gniazd połączeniowych.

6. Obciążenie wstępne i odciążenie - kontrola poprawności działania tensometru.

7. Równoważenie zgrubne i dokładne torów pomiarowych.

8. Wzorcowanie torów pomiarowych wg. wzoru 18

9. Obciążenie próbki siłą wstępną F₀ = 8 kN, a następnie wykonanie odczytów na wyświetlaczu mostka tensometrycznego dla poszczególnych kanałów pomiarowych i zanotowanie ich w tabeli pomiarowej.

10. Zwiększenie obciążenia co 8 kN, a następnie odczytanie i zapisanie nowych wartości odkształcenia .

11. Obciążanie próbki siłą w zakresie proporcjonalności.

12. Rejestracja i opracowanie wyników.

4.4 Opracowanie wyników badań:

Tabela pomiarowa

Próbka stalowa …….. x ……. mm - S₀ =

Obciążenie [kN]	Odczyty na wyświetlaczu mostka tensometrycznego [µm/m]
		1	2	3	4
F0
F1
F2
F3
	Δε1 =	Δε2 =	Δε3 =	Δε4 =
		Δε1,2 =		Δε3,4 =

Należy odczytać i zanotować w tabeli pomiarowej przyrosty odkształceń poszczególnych czujników (dla czujników poprzecznych będą one ujemne), a następnie obliczyć średnie wartości dla kierunku podłużnego Δε_1,2 i poprzecznego Δε_3,4.

Wartość modułu Younga można wyznaczyć w oparciu o prawo Hooke'a z wzoru:

[17]

Liczba Poissona jest natomiast stosunkiem skrócenia poprzecznego (-Δε_3,4) do wydłużenia w kierunku rozciągania Δε_1,2

[18]

Moduł odkształcenia postaciowego (Kirchhoffa) G można określić z teoretycznej zależności

[19]

4.5 Wzorcowanie za pomocą mostka z rezystorem bocznikującym w jednej gałęzi

Wzorcowanie za pomocą rezystora bocznikującego jest szeroko stosowane w sytuacji gdy używa się przetworników rezystancyjnych o małych względnych zmianach rezystancji, pracujących w układzie mostka Wheatstone'a. Zasadę wzorcowania za pomocą rezystora bocznikującego przedstawia rys. 8.

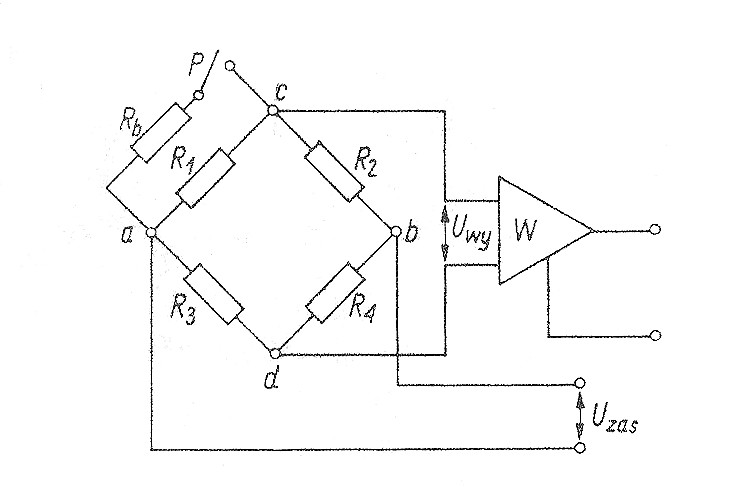
Rys. 8 Schemat układu do wzorcowania z zastosowaniem rezystora bocznikującego R_b; U_zas - napięcie zasilania, U_wy - napięcie wyjściowe, W - wzmacniacz mostka tensometrycznego.

Zmniejszenie rezystancji R pojedynczej gałęzi mostka symetrycznego (R₁=R₂=R₃=R₄ =R), spowodowane dołączeniem rezystora bocznikującego R_b można określić na podstawie zależności

[20]

stąd

[21]

Podstawiając znaną zależność
otrzymujemy ostatecznie zależność:

[22]

Znając zatem wartość stałej tensometru K i przyjmując dla przetwornika daną wartość odkształcenia ε można określić odpowiadającą temu odkształceniu wartość R_b.

Przykładowo dla R=100 Ω, K = 2,00 i ε = 0,1% = 0,001 wartość R_b= 49,9 kΩ.

5. Metodyka wyznaczenia współczynnika sprężystości podłużnej przy osiowym rozciąganiu.

Współczynnik sprężystości podłużnej dotyczy zakresu proporcjonalności naprężeń i odkształceń, gdzie zastosowanie ma prawo Hooke'a (wzór 3). Przy osiowym rozciąganiu jest to równoznaczne z warunkiem nie przekroczenia granicy proporcjonalności R_H przez największą wartość naprężenia w próbce. Ten warunek jest zwykle spełniony wówczas gdy
. Do tego typu porównań , zamiast granicy proporcjonalności R_H , używa się często granicy sprężystości
(wzór 5) wyznaczanej w sposób bardziej jednoznaczny i dokładniejszy w trakcie ścisłej próby rozciągania metali. Wartości obu tych granic są do siebie bardzo zbliżone - patrz rys. 5.

[23]

- umowna granica sprężystości - naprężenie odpowiadające działaniu siły rozciągającej, wywołującej w próbce umowne wydłużenie trwałe x, wynoszące 0,05% długości pomiarowej L₀; w technicznie uzasadnionych przypadkach dopuszcza się określenie granicy sprężystości przy wydłużeniach trwałych mniejszych niż 0,05%.

Wartości modułu Younga wyznacza się zawsze z pominięciem niewielkiego zakresu małych obciążeń , odpowiadających naprężeniom mniejszym niż 0,1 R_H . Przyjmujemy więc pewną wartość naprężenia wstępnego. Dzięki temu można uniknąć wpływu na wyniki pomiarów takich czynników, jak:

• nieco inne własności mechaniczne materiału przy bardzo małych obciążeniach niż w dalszym, interesującym nas zakresie;

• mniej dokładne wskazania maszyny wytrzymałościowej w pobliżu zera;

• dokładność przyrządów służących do pomiaru odkształceń w początkowej fazie ich działania (n.p. luzy w połączeniach dźwigni tensometrów mechanicznych;

• niedokładności związane ze sposobem podparcia itp.

Na rys. 6 pokazano przykłady początkowych części wykresów
ilustrujących wpływ wymienionych czynników. W analizie wyników należy brać pod uwagę wykres, którego początek określa się drogą ekstrapolacji liniowej jego części.

Rys. 9 Odchylenia w początkowej fazie wykresów

Z wykresów przedstawionych na rys. 9 wynika, że do określenia wartoś­ci modułu Younga przy rozciąganiu, zbędne jest wykonywanie wykresu
, jeśli zastosujemy obciążenie wstępne F₀ (odpowiadające na rysunku wartości naprężenia σ₀ przyjmowanego jako σ = 0,lR_s) oraz znamy w przybliżeniu wartość granicy sprężystości R_s, dzięki czemu możemy ustalić obciążenie maksymalne F₁ (odpowiadające na rysunku wartości naprężenia σ₁, przyjmowanego jako σ₁ = 0,9R_s).

Współczynnik sprężystości wzdłużnej E można obliczyć z prawa Hooke'a, które dla potrzeb obliczeń zapisuje się często w postaci (patrz wzór nr 17):

[24]

gdzie
oraz
są odpowiadającymi sobie przyrostami wartości naprężeń i odkształceń.

Określony w ten sposób moduł Younga nazywa się czasami modułem „siecznym”. Wynika to z jego interpretacji geometrycznej, gdzie jest on równy tangensowi nachylenia siecznej poprowadzonej na wykresie
przez punkty o współrzędnych (
) i (
) - por. rys. 7. Rzeczywisty bowiem kształt wykresu
zawsze w pewnym stopniu odbiega od prostoliniowego.

Przy znacznym odchylaniu się wykresu od linii prostej, moduł Younga wyznacza się jako średnią z modułów siecznych, określonych wg wzoru 7 i rys. 7 (na tym rysunku wykres celowo przesadnie zakrzywiono).

[25]

gdzie:

[25a]

Rys.10 Moduły sieczne na wykresie

Omówione na przykładzie rozciągania problemy badawcze i interpretacyjne będą odnosiły się, po pewnych modyfikacjach, również do prób ściskania, zginania i skręcania, którymi będziemy się zajmować w dalszej kolejności.

To i następne ćwiczenia będą polegały na wyznaczeniu stałych materiałowych dla różnych materiałów konstrukcyjnych, przy zastosowaniu różnorodnych technik pomiarowych.

Stałymi materiałowymi najczęściej wyznaczanymi w badaniach laboratoryjnych materiałów konstrukcyjnych są:

• współczynnik sprężystości wzdłużnej (moduł Younga) E;

• moduł sprężystości poprzecznej (odkształcenia postaciowego - moduł Kirchhoffa) G (zwany także modułem skręcania, ścinania);

• liczba Poissona ν.

Spośród tych trzech stałych tylko dwie są niezależne. Oznacza to, że mając dwu dowolnych z nich, można obliczyć trzecią z zależności nr 19.

W poniższej tabeli podano orientacyjne wartości stałych materiałowych dla niektórych materiałów.

Tabela nr 1

Materiał	E [GPa]	G [GPa]	ν
Stal	196 - 210	78 - 81	0,29 - 0,30
Stopy aluminium	69-75	25 - 28	0,23 - 0,27
Miedź	110 - 130	40 - 49	0,30 -0,33
Beton	12 - 38	-	0,12 - 0,18
Szkło	60 - 70	22 - 27	0,20 - 0,27
Drewno	9 - 12	-	-
Kauczuk	do 0,008	-	Ok. 0,48

7. Opracowanie wyników i wytyczne do sprawozdania

Sprawozdanie powinno zawierać:

1. Cel ćwiczenia

2. Krótki wstęp teoretyczny

3. Zestawienie wyników pomiarów zgodne z przykładową tabelą pomiarową

4. Opracowanie statystyczne wyników pomiarów

5. Obliczenie modułu sprężystości podłużnej E, liczby Poissona ν i modułu Kirchhoffa G

6. Wnioski z ćwiczenia .

8. Literatura

1. Dyląg Z., Jakubowicz A., Orłoś Z.; Wytrzymałość materiałów. Tom I, Wydawnictwa Naukowo - Techniczne, Warszawa 1999.

2. Joniak Stefan ; Badania eksperymentalne w wytrzymałości materiałów. Wydawnictwo Politechniki Poznańskiej, Poznań 2006.

3. Burczyński Tadeusz; Laboratorium z wytrzymałości materiałów. Wydawnictwo Politechniki Śląskiej, Gliwice 2002.

1

1

---