MECHANIKA.

Kinematyka punktu - opis ruchu punktu, układu punktów, bryły sztywnej lub układów brył sztywnych, bez wnikania w przyczyny ruchu.

Wielkościami charakteryzującymi ruch są: przemieszczenie, prędkość, przyspieszenie.

W celu opisania ruchu posługujemy się układami odniesienia względem których badamy ruch.

Kartezjański płaski układ odniesienia w którym ruch punktu opisujemy względem osi X i Y względem punktu O.

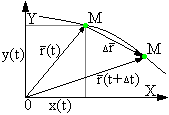
Jednoznaczny opis ruchu w postaci wektorowej
po przez określenie przyrostu wektora.

Kartezjański płaski układ współrzędnych.

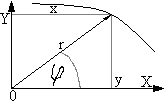
Układ biegunowy.

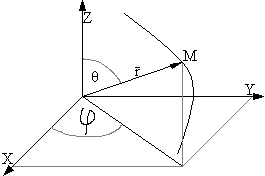
Kartezjański przestrzenny układ współrzędnych.

Układ walcowy.

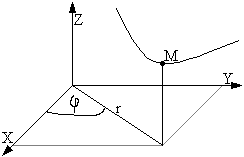
r'=r(t)

z=z(t)

wektorowe równanie ruchu - jednoznacznie określa położenie.

Prędkość punktu

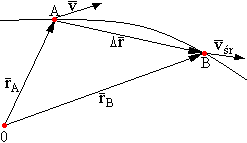
Wyznaczanie wektora prędkości punktu. Prędkość średnia jest stosunkiem przyrostu
do przyrostu Δt.

Przyspieszenie punktu.

Przyspieszeniem średnim nazywamy stosunek przyrostu prędkości Δv do przyrostu czasu Δt.

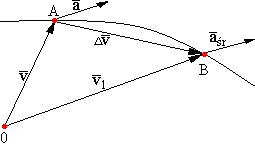
Miejsce geometryczne końców wektorów prędkości, których początki sprowadzono do jednego punktu nazywamy hodografem prędkości.

Klasyfikacja ruchu:

Wielkości charakterystyczne: tor, prędkość, przyspieszenie.

1. tor - ruch prostoliniowy i krzywoliniowy,

2. prędkość - ruch jednostajny i zmienny,

3. przyspieszenie - ruch jednostajnie przyspieszony i zmienny.

Kinematyka bryły sztywnej:

Bryłą sztywna - nazywamy zbiór punktów, których wzajemne odległości są stałe.

Liczbą stopni swobody - nazywamy liczbę niezależny współrzędnych potrzebnych do określenia położenia punktów lub ryły w przestrzeni.

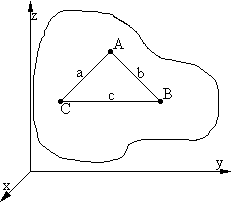
Położenie bryły w przestrzeni określone przez trzy punkty.

A(x_A, x_A, x_A)

B(x_B, x_B, x_B)

C(x_C, x_C, x_C)

Równania maja postać:

Sześć współrzędnych wystarcza do określenia jednoznacznie dowolnego ruchu swobodnego. Dowolna bryła ma sześć stopni swobody lub mniej. Przykłady:

Jeden stopień swobody.

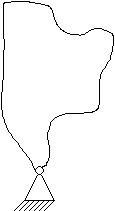
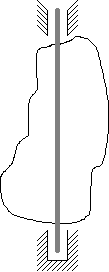
Trzy stopnie swobody.

Bryły sztywne mogą wykonywać:

1. Ruch postępowy ( ruch jednoparametrowy ).

2. Ruch obrotowy.

3. Ruch płaski.

4. Ruch złożony ( względny ).

5. Ruch kulisty.

6. Ruch ogólny.

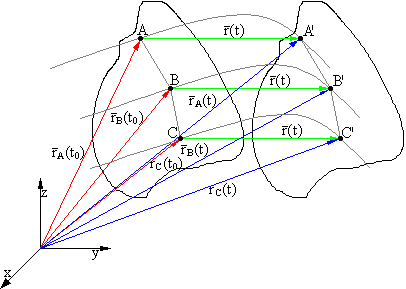
Ruchem postępowym bryły sztywnej nazywamy taki ruch w którym wszystkie punkty bryły doznają tych samych przesunięć. Jest to najprostszy przypadek ruchu bryły sztywnej zwany jednoparametrowym ( wystarczy podać tylko jedną wielkość określającą ruch aby jednoznacznie opisać ruch bryły ).

Równania ruchu poszczególnych punktów:

Prędkość punktów w ruchu postępowym, wektor prędkości:

Wektor przyspieszenia:

Ruch obrotowy bryły sztywnej. Jeżeli unieruchomimy dwa dowolne punkty bryły sztywnej, to wszystkie punkty leżące na prostej łączącej dwa unieruchomione punkty ( będące nieruchome, stanowiące oś obrotu ) będą mogły poruszać się po okręgach w płaszczyznach prostopadłych do osi obrotu o środkach na niej leżących.

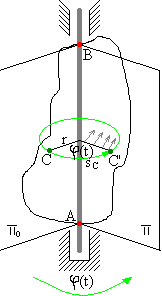
Tor każdego ciała poruszającego się ruchem obrotowym jest okręgiem leżącym w płaszczyźnie prostopadłej do osi obrotu o środku leżącym na tej osi i opisany jest promieniem o długości równej odległości punktu od osi obrotu.

s_C=φ(t)·r

Prędkość liniowa punktu:

Prędkość kątowa ω.

WIELKOŚCI KĄTOWE W RUCHU OBROTOWYM ( określają ruch całej bryły )		WIELKOŚCI LINIOWE W RUCHU OBROTOWYM ( dotyczą tylko określonego punktu )
	- droga [rad]	[m]	s
	- prędkość [rad/s]	[m/s]
	- przyspieszenie [rad/s^2]	[m/s^2]

s_c=φ(t)·r

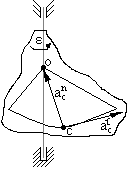
Kierunek przyspieszenia normalnego równoległy do promienia CO, zwrot od C do O.

Przyspieszenie styczne:
Kierunek przyspieszenia stycznego prostopadły do promienia, zwrot zgodny ze zwrotem ε.

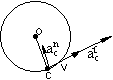
Ruch płaski bryły sztywnej. Ruchem płaskim ciała sztywnego nazywamy ruch w którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do płaszczyzny zwanej płaszczyzną kierującą.

Ruch płaski bryły sztywnej można przedstawić:

1. jako przemieszczenie i obrót,

2. jako obrót wokół szczególnego punktu.

Ruch płaski jako złożenie przemieszczenia i obrotu:

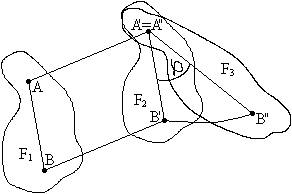
Równania:

x_A=x_A(t) x_B=x_B(t)

y_A=y_A(t) y_B=y_B(t)

Rych obrotowy:

Obrót wokół chwilowego środka obrotu:

Twierdzenie Oilera - dowolne przemieszczenie figury płaskiej w jej płaszczyźnie, może być dokonane za pomocą pewnego punktu zwanego środkiem obrotu. Wokół każdego środka, obrót trwa nieskończenie krótko, dlatego też punkty te nazywamy chwilowymi środkami obrotu.

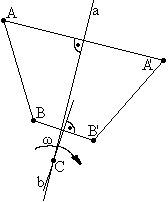
a, b - symetralne odcinków

C - środek obrotu - wraz z ruchem ciała przemieszcza się

Metody wyznaczania prędkości w ruchu płaskim:

1. Metoda analityczna.

2. Metoda rzutów prędkości.

3. Metoda superpozycji.

4. Metoda chwilowego środka obrotu.

5. Metoda prostej przechodniej.

6. Metoda prędkości odwróconych.

Ad1. Metoda analityczna - polega na zróżniczkowaniu względem czasu równań ruchu rozpatrywanego punktu ciała sztywnego.

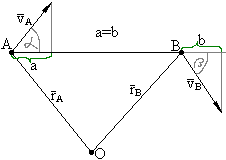
Ad2. Metoda rzutów prędkości - oparta jest na twierdzeniu Charlesa.

Twierdzenie Charlesa - w bryle sztywnej podczas dowolnego ruchu, rzuty wektorów prędkości dwóch dowolnych punktów na prostą łączącą te punkty są sobie równe.

v_Acosα=v_Bcosβ

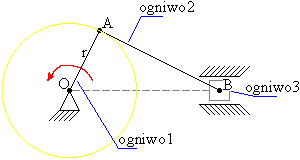
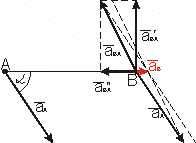
Zad. Korzystając z rzutów prędkości wyznaczyć prędkość B ogniwa mechanizmu korbowo-wodzikowego w położeniu przedstawionym na rysunku, jeśli korba OA obraca się z prędkością ω=2[rad/s]=const. OA=0,2m; AB=0,6m; α=60˚.

Kierunek prędkości B jest znany gdyż ogniwo 3 może poruszać się tylko w jeden sposób.

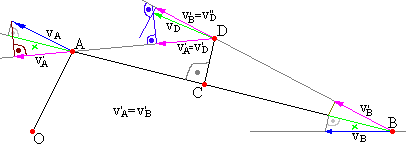
Ad3. Metoda superpozycji:

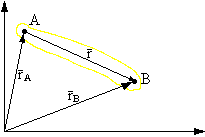
- zmienia się zwrot i kierunek

Prędkość dowolnego punktu w ruchu płaskim stanowi sumę geometryczną wektora punktu przyjętego jako biegun oraz wektora prędkości w ruchu obrotowym punktu szukanego względem bieguna.

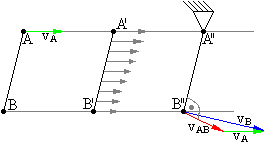
Kierunek prędkości
jest prostopadły do odcinka BA, a dodani
i
daje wartość
.

ω taka sama

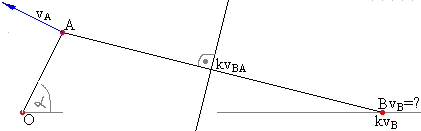
v_B||do prowadnic

Odkładamy siłę v_A ( znamy ją ) oraz kierunki sił v_B, i v_BA - tworzymy plan prędkości z którego odczytujemy wartości sił nieznanych.

Tocząca się tarcza.

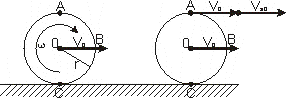
V_C=0

kV_C0
C0

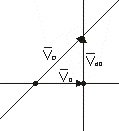
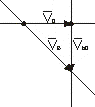
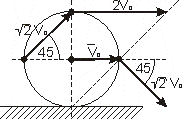
Ad4. Metoda chwilowego środka prędkości. Przemieszczenie ciała w ruchu płaskim można przedstawić jako obrót dokoła punktu zwanego chwilowym środkiem obrotu.

Chwilowym środkiem obrotu nazywamy w danym położeniu, taki punkt S przekroju dla którego w danej chwili prędkość liniowa równa jest zero.

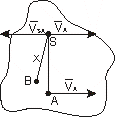
W celu wyznaczenia chwilowego środka prędkości wystawiamy prostopadłe do kierunków prędkości dwóch punktów badanego przekroju poruszającego się ruchem płaskim, punkty przecięcia dają chwilowy środek prędkości.

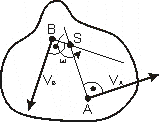
UWAGA! Może być ułożenie wektorów prędkości dla których niema punktu chwilowego obrotu.

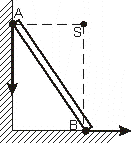
DEFINICJA CENTROIDY:

Ruch płaski możemy rozpatrywać jako wiele następujących po sobie obrotów chwilowych w około przemieszczającego się ośrodka obrotu. Kolejne położenia środków w układzie nieruchomym nazywamy cętroidą stałą, zaś w układzie ruchomym cętroidą ruchomą.

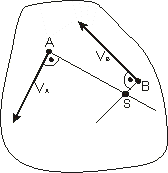
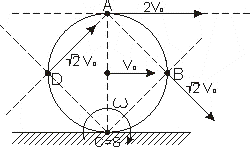
Przyspieszenie w ruchu płaskim.

Metoda super pozycji.

BA

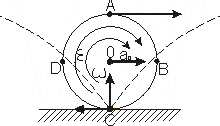
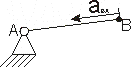
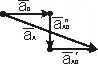
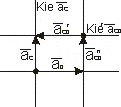
Chwilowy środek przyspieszeń.

W ruchu płaskim bryły w każdej chwili istnieje punkt , którego przyspieszenie jest równe zero - punkt ten nazywamy chwilowym środkiem przyspieszeń.

Zakładając, że a_p=0 przyspieszenie punktu P obliczonego metodą superpozycji, będzie wynosić:

a_P - przyspieszenie chwilowe środka przyśpieszeń:

Odległość chwilowego środka prędkości od punktu A wynosi:

Dane: a_A=2m/s²⁺ a_B=4m/s² l=1m β=30˚

Szukane: ε, ω=?

P=?

Ruch punktu bryły sztywnej poruszającej się ruchem złożonym - ruch złozony punktu.

Ruch punktu M względem nieruchomego punktu  odniesienia 0XYZ nazywamy ruchem bezwzględnym.

Ruch punktu M względem ruchomego układu odniesienia 0'xyz nazywamy ruchem względnym.

Ruch układu ruchomego 0'xyz względem układu nieruchomego 0XYZ nazywamy ruchem unoszenia.

Prędkość i przyspieszenie w ruchu złożonym.

zmienia kierunek bez zmiany wartości

                                                                       ω_u=2rad/s

ζ(t)=2t²[m]

l=8m

     Szukane:

V_m(t_l)

                               

                           

                        

Przyspieszenie punktów w ruchu złożonym.

Przyspieszenie bezwzględne punktu M=
jest równe pochodnej względem czasu prędkości bezwzględnej
tego punktu

gdzie:

więc:

Przyspieszenie coriolisa jest podwójnym iloczynem wektorowym prędkości kątowej unoszenia i prędkości względnej:

Przyspieszenie coriolisa nie występuje czyli jest równe zero, kiedy:

1. Ruchem unoszenia są ruchy: prostoliniowy, harmoniczny, prosty i postępowy:
   

2. Gdy wektory prędkości kątowej
   jest równoległy do wektora prędkości względnej
   

3. W przypadku kiedy prędkość względna
   będzie równa zero
   , przyspieszenie coriolisa jest wektorem
   do płaszczyzny utworzonej przez wektory
   .

Zwrot przyspieszenia coriolisa zgodny jest z regułą śruby prawo skrętnej

Wartość:

                r=0,2m

                α=60˚

           

           

          t=3[s]

            

          

                           v_A'=v_B'

                         v_A=v_B

        

        

Ruch postępowy, a więc przyspieszenie coriolisa jest równe zero.

bo prędkość unoszenia jest równoległa do prędkości

Ruch kulisty - jest to taki ruch ciała sztywnego podczas którego jeden punkt zwany środkiem ruchu kulistego jest nieruchomy, zaś torami pozostałych punktów są powierzchnie kuli o środku w punkcie będącym środkiem ruchu kulistego.

Ruch kulisty opisujemy przy pomocy kątów Eulera.

                                                 φ - kąt obrotu własnego

                        ψ - kąt precesji

             
-kąt nutacji

Kąty Eulera:

Podczas ruchu ciała sztywnego wartości kątów obrotu własnego, precesji, nutacji zmieniają się w czasie:

Aby jednocześnie określić ruch należy podać trzy równania.

Ruch ciała sztywnego w ruchu kulistym ma trzy stopnie swobody.

Prędkość kątowa w ruchu kulistym.

- prędkość kątowa obrotu własnego

- prędkość kątowa precesji

- prędkość kątowa nutacji

Prędkość kątowa wyrażona jest jako suma geometryczna:

Prędkość dowolnego punktu w ruchu kulistym.

OBROTOWY KULISTY

   ω - chwilowa

Przyspieszenie w ruchu kulistym.

, stąd:

a_o - przyspieszenie obrotowe,

a_D - przyspieszenie do osiowe.

Precesja regularna: kąt nutacji jest stały, a prędkość nutacji równa się zero - wartości prędkości obrotu własnego i precesji są stałe.

Prędkość kątowa precesji wynosi:

Suma geometryczna:

Przyspieszenie kątowe:

Wektor przyspieszenia kątowego
jest prostopadły do płaszczyzny wyznaczonej wektorami
oraz
.

         1. Szukamy chwilowej osi obrotu dla danego położenia.

Prędkość punktów leżących na chwilowej osi obrotu jest równa 0.

2. Szukamy punktów nieruchomych ( 1, 2 ) jest to oś
   .

Ruch bryły swobodnej.

Położenie bryły sztywnej w ruchu dowolnym będzie jednoznacznie określone jeżeli w danej chwili czasowej będą znane współrzędne ruchomego układu   x₀(t), y₀(t), z₀(t) oraz kąty
,
,
.

Dynamika.

Bezwładnościowy inercyjny lub absolutny układ odniesienia ( układ odniesienia Galileusza ) - jest to taki układ, w którym obowiązują prawa Newtona. Układ sztywno związany z ziemią, gdyż wartości przyspieszeń związanych z ruchem ziemi w porównaniu z przyspieszeniem grawitacyjnym możemy pominąć.

I i II zadanie dynamiki.

Dynamika swobodnego punktu materialnego.

Dynamiczne wektorowe różniczkowe równanie ruchu swobodnego punktu materialnego ma postać:

siła zależy od prędkości, promienia, czasu.

I zadanie dynamiki -odwrotne.

Jakie siły powodują ściśle określony ruch.

W I zadaniu dynamiki należy wyznaczyć wartość i kierunek wypadkowej sił działającej na punkt materialny znając masę punktu i jego równanie ruchu.

Jeżeli ruch punktu opisany jest wektorem-promieniem wodzącym
, wówczas przyspieszenie
.

Według II prawa Newtona, siła działająca na omawiany punkt jest równa:
.

W kartezjańskim układzie współrzędnych: x=x(t), y=y(t), z=z(t)

II drugie zadanie dynamiki - proste.

II zadanie dynamiki polega na wyznaczeniu równań ruchu punktu materialnego znając jego masę i działające siły.

Zadanie to sprowadza się do całkowania różniczkowych równań ruchu w których stałe całkowania wyznaczamy z warunków początkowych.

Warunki początkowe to dla t=0 położenia punktu opisane za pomocą współrzędnych x=x₀, y=y₀, z=z₀.

Zaś prędkości:
.

Dynamiczne różniczkowe równanie ruchu:
.

Aby uzyskać równanie ruchu, należy:
.

Zasad Da Lamberta.

Na punkt materialny M działają siły rzeczywiste, które w każdej chwili równoważą się z siłą bezwładności tego punktu, tzw. Siłą Da Lamberta.

Siłą bezwładności ( lub siłą Da Lamberta ) nazywamy fikcyjną siłę               
równą co do wartości iloczynowi masy i przyspieszenia punktu                     materialnego lecz przeciwnie do tego przyspieszenia skierowana.

W układzie Kartezjańskim:

Z równania
wynikają następujące równania różniczkowe:
.

Przykład.

Punkt materialny o masie m wyrzucony jest z prędkością początkową v₀ pod kątem α do poziomu - wyznacz wysokość i zasięg rzutu.

13

---