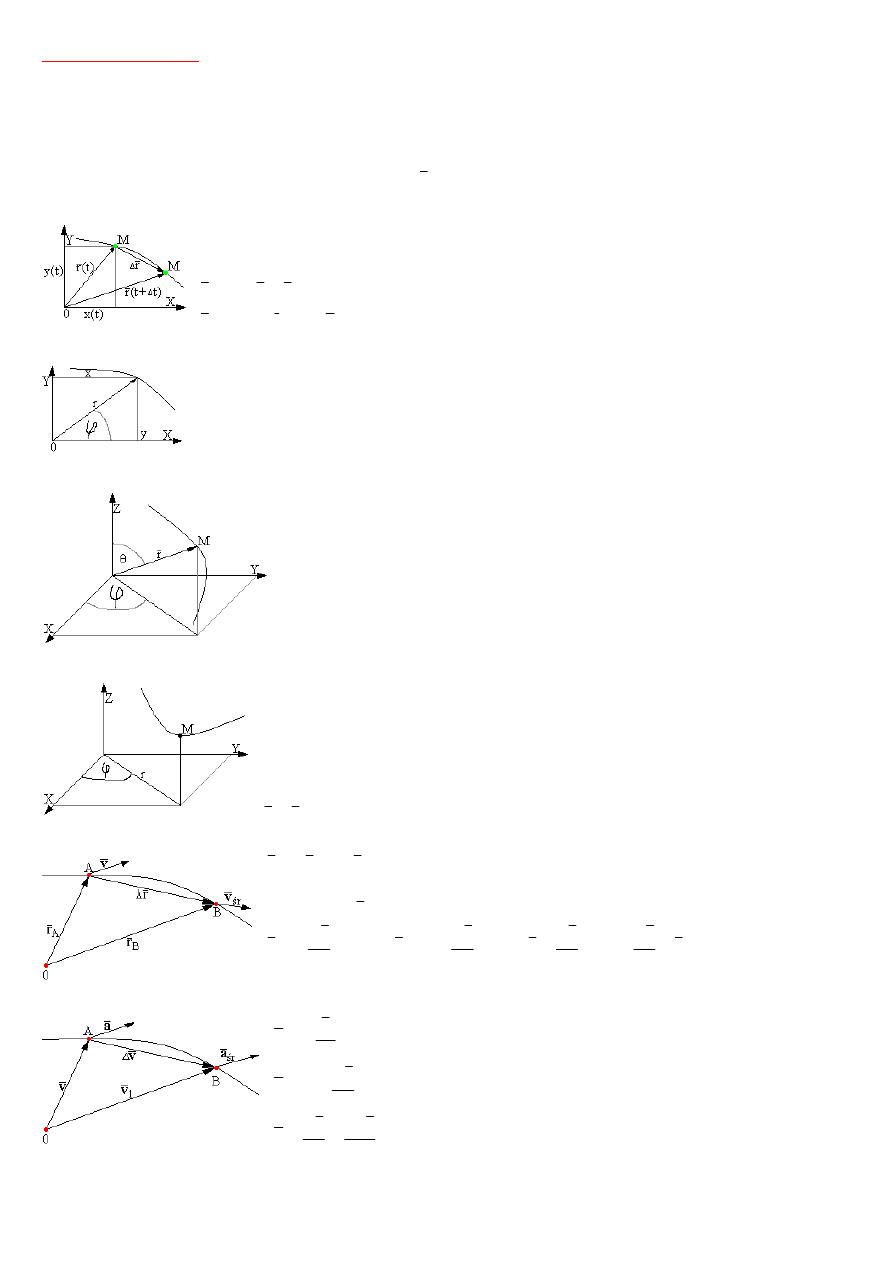
1

Kinematyka punktu

– opis ruchu punktu, układu punktów, bryły sztywnej lub układów brył sztywnych,

bez wnikania w przyczyny ruchu.
Wielkościami charakteryzującymi ruch są: przemieszczenie, prędkość, przyspieszenie.
W celu opisania ruchu posługujemy się układami odniesienia względem których badamy ruch.
Kartezjański płaski układ odniesienia w którym ruch punktu opisujemy względem osi X i Y względem
punktu O.

Jednoznaczny opis ruchu w postaci wektorowej

)

(t

r

po przez określenie przyrostu wektora.

Kartezjański płaski układ współrzędnych.

j

t

y

i

t

x

t

r

t

t

r

r

t

r

)

(

)

(

)

(

)

(

)

(















Układ biegunowy.











)

(

)

(

t

t

r

r























sin

cos

r

y

r

x

Kartezjański przestrzenny układ współrzędnych.





















)

(

)

(

)

(

t

t

t

r

r





Układ walcowy.

r’=r(t)

)

(t



 

z=z(t)

wektorowe równanie ruchu – jednoznacznie określa położenie.

)

(t

r

r 

Prędkość punktu

r

r

r

A

B







Wyznaczanie wektora prędkości punktu. Prędkość średnia jest stosunkiem

przyrostu

r

 do przyrostu Δt.

t

r

v

śr







t

r

v

t











0

lim

dt

r

d

v 



 r

dt

r

d

Przyspieszenie punktu.

Przyspieszeniem średnim nazywamy stosunek przyrostu prędkości Δv do przyrostu czasu Δt.

t

v

a

śr





t

v

a

t











0

lim

2

2

dt

r

d

dt

v

d

a





2

Miejsce geometryczne końców wektorów prędkości, których początki sprowadzono do jednego punktu
nazywamy hodografem prędkości.
Klasyfikacja ruchu:
Wielkości charakterystyczne: tor, prędkość, przyspieszenie.

a) tor – ruch prostoliniowy i krzywoliniowy,
b) prędkość – ruch jednostajny i zmienny,
c) przyspieszenie – ruch jednostajnie przyspieszony i zmienny.

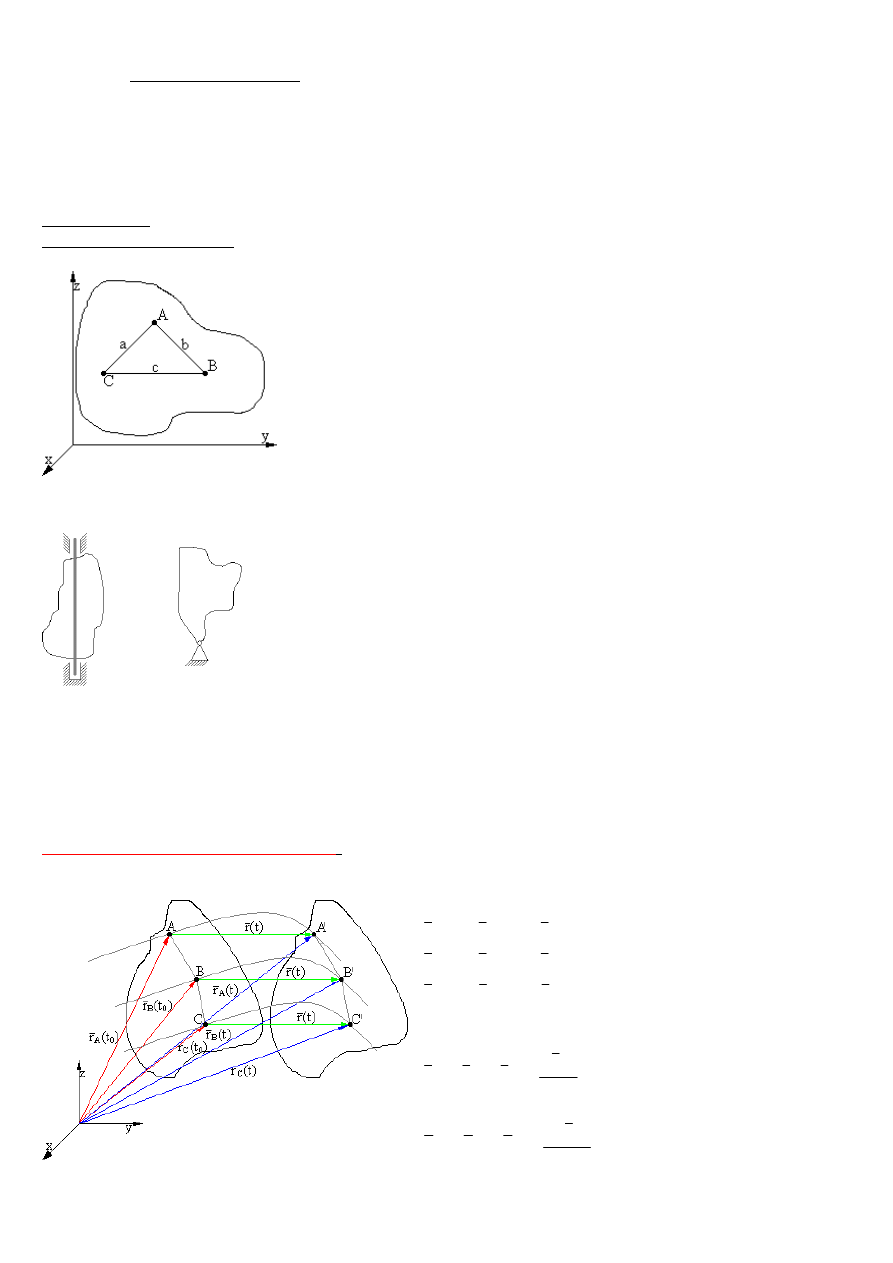
Kinematyka bryły sztywnej:
Bryłą sztywna – nazywamy zbiór punktów, których wzajemne odległości są stałe.
Liczbą stopni swobody – nazywamy liczbę niezależny współrzędnych potrzebnych do określenia
położenia punktów lub ryły w przestrzeni.

Położenie bryły w przestrzeni określone przez trzy punkty.
A(x

A

, x

A

, x

A

)

B(x

B

, x

B

, x

B

)

C(x

C

, x

C

, x

C

)

Równania maja postać:



















































































2

2

2

2

2

2

2

2

2

2

2

2

c

z

z

y

y

x

x

b

z

z

y

y

x

x

a

z

z

y

y

x

x

B

C

B

C

B

C

A

B

A

B

A

B

C

A

C

A

C

A

Sześć współrzędnych wystarcza do określenia jednoznacznie dowolnego

ruchu swobodnego. Dowolna bryła ma sześć stopni swobody lub mniej. Przykłady:
Jeden stopień swobody.

Trzy stopnie swobody.

Klasyfikacja ruchu brył:

1) Ruch postępowy ( ruch jednoparametrowy ).
2) Ruch obrotowy.
3) Ruch płaski.
4) Ruch złożony ( względny ).
5) Ruch kulisty.
6) Ruch ogólny.

Ruchem postępowym bryły sztywnej

nazywamy taki ruch w którym wszystkie punkty bryły doznają

tych samych przesunięć. Jest to najprostszy przypadek ruchu bryły sztywnej zwany jednoparametrowym
( wystarczy podać tylko jedną wielkość określającą ruch aby jednoznacznie opisać ruch bryły ).

Równania ruchu poszczególnych punktów:

 

 

 

 

 

 

t

r

t

r

t

r

t

r

t

r

t

r

t

r

t

r

t

r

C

C

B

B

A

A













)

(

)

(

)

(

0

0

0

Prędkość punktów w ruchu postępowym, wektor
prędkości:

 

dt

t

r

d

v

v

v

C

B

A







Wektor przyspieszenia:

 

2

2

dt

t

r

d

a

a

a

C

B

A







3

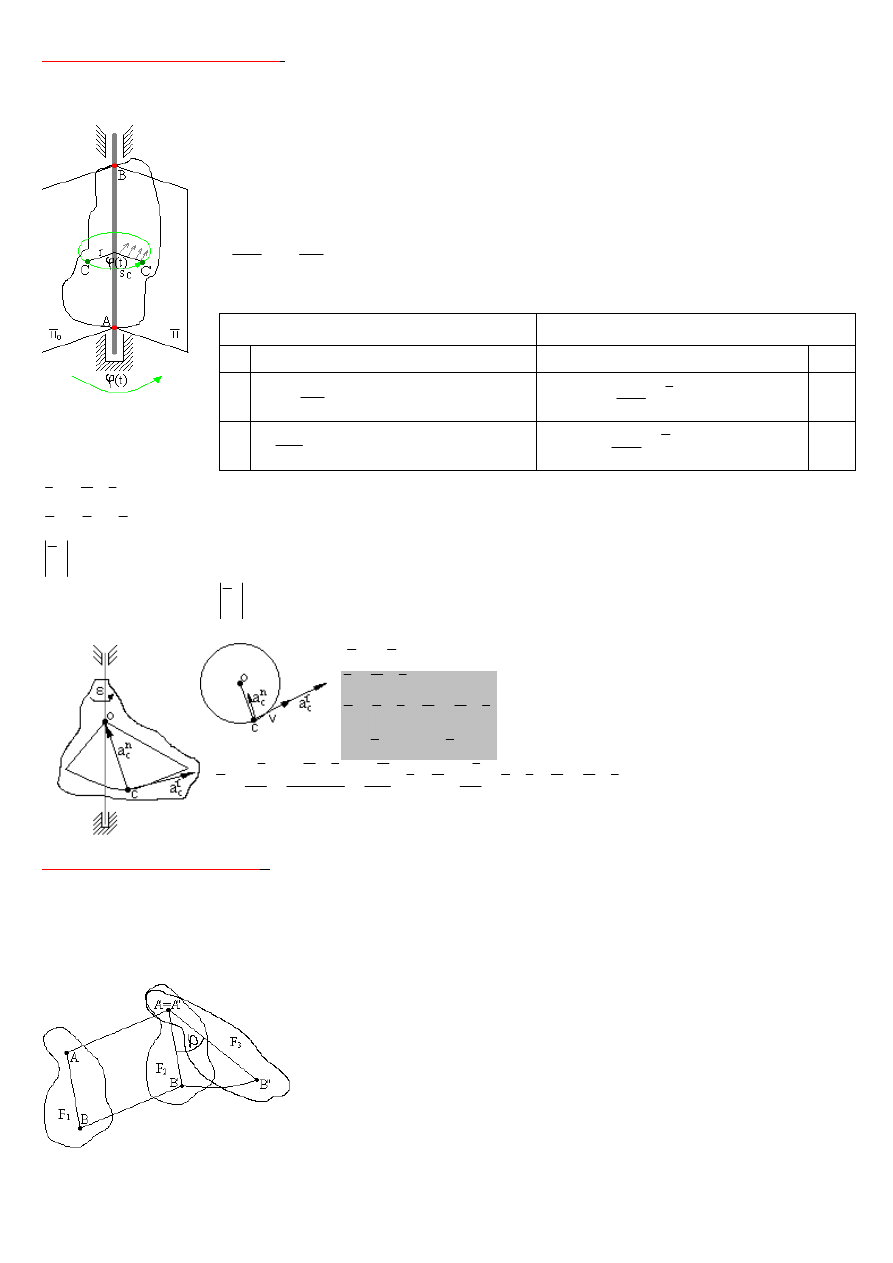
Ruch obrotowy bryły sztywnej

. Jeżeli unieruchomimy dwa dowolne punkty bryły sztywnej, to wszystkie

punkty leżące na prostej łączącej dwa unieruchomione punkty ( będące nieruchome, stanowiące oś
obrotu ) będą mogły poruszać się po okręgach w płaszczyznach prostopadłych do osi obrotu o środkach
na niej leżących.

Tor każdego ciała poruszającego się ruchem obrotowym jest okręgiem leżącym w
płaszczyźnie prostopadłej do osi obrotu o środku leżącym na tej osi i opisany jest
promieniem o długości równej odległości punktu od osi obrotu.
s

C

=φ(t)·r

Prędkość liniowa punktu:

 

 

r

t

r

t

dt

d

r

dt

ds

v

C























Prędkość kątowa ω.

s

c

=φ(t)·r

c

c

r

v









c

n
c

c

a

a

a





r

a

n
c





2



Kierunek przyspieszenia normalnego równoległy do promienia CO, zwrot od C do O.

Przyspieszenie styczne:

r

a

c









Kierunek przyspieszenia stycznego prostopadły do promienia, zwrot

zgodny ze zwrotem ε.



c

n
c

a

a 





n

r

r

a

r

v

a

a

































r

r

dt

r

d

r

dt

d

dt

r

d

dt

v

d

a





































Ruch płaski bryły sztywne

j. Ruchem płaskim ciała sztywnego nazywamy ruch w którym wszystkie

punkty ciała poruszają się w płaszczyznach równoległych do płaszczyzny zwanej płaszczyzną kierującą.
Ruch płaski bryły sztywnej można przedstawić:

a) jako przemieszczenie i obrót,
b) jako obrót wokół szczególnego punktu.

Ruch płaski jako złożenie przemieszczenia i obrotu:

Równania:
x

A

=x

A

(t) x

B

=x

B

(t)

y

A

=y

A

(t) y

B

=y

B

(t)

Rych obrotowy:

 

t



 

WIELKOŚCI KĄTOWE W RUCHU OBROTOWYM

( określają ruch całej bryły )

WIELKOŚCI LINIOWE W RUCHU OBROTOWYM

( dotyczą tylko określonego punktu )



 

t



 

- droga [rad]

 

t

s

s

C

C





[m]

s









dt

d

- prędkość [rad/s]

c

C

v

dt

ds



[m/s]

s











dt

d

- przyspieszenie [rad/s

2

]

C

C

a

dt

dv



[m/s

2

]

s



4

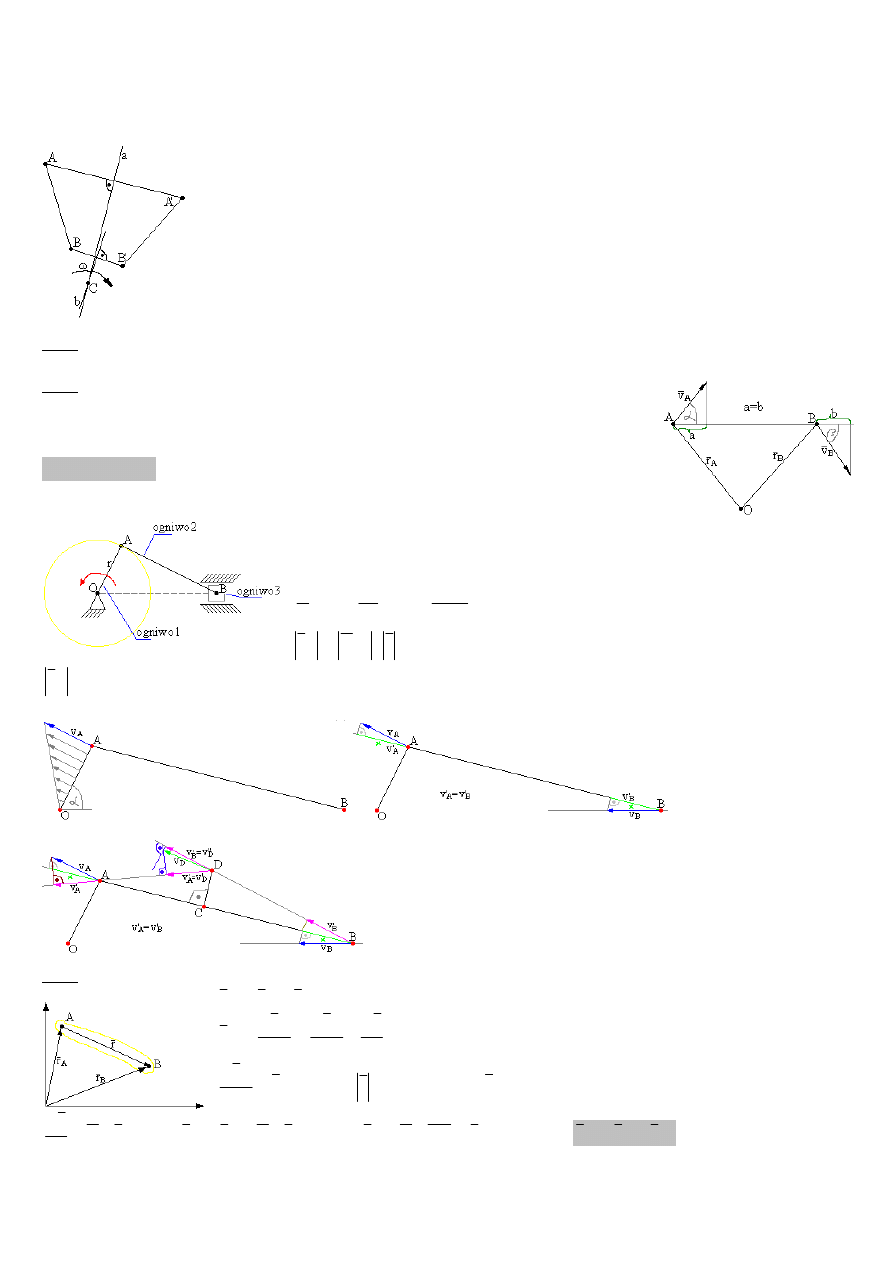
Obrót wokół chwilowego środka obrotu:
Twierdzenie Oilera – dowolne przemieszczenie figury płaskiej w jej płaszczyźnie, może być dokonane za
pomocą pewnego punktu zwanego środkiem obrotu. Wokół każdego środka, obrót trwa nieskończenie
krótko, dlatego też punkty te nazywamy chwilowymi środkami obrotu.

a, b – symetralne odcinków
C – środek obrotu – wraz z ruchem ciała przemieszcza się

Metody wyznaczania prędkości w ruchu płaskim:

1. Metoda analityczna.
2. Metoda rzutów prędkości.
3. Metoda superpozycji.
4. Metoda chwilowego środka obrotu.
5. Metoda prostej przechodniej.
6. Metoda prędkości odwróconych.

Ad1.

Metoda analityczna

– polega na zróżniczkowaniu względem czasu równań ruchu rozpatrywanego

punktu ciała sztywnego.
Ad2.

Metoda rzutów prędkości

– oparta jest na twierdzeniu Charlesa.

Twierdzenie Charlesa – w bryle sztywnej podczas dowolnego ruchu, rzuty
wektorów prędkości dwóch dowolnych punktów na prostą łączącą te punkty
są sobie równe.
v

A

cos

α

=v

B

cosβ

Zad. Korzystając z rzutów prędkości wyznaczyć prędkość B ogniwa
mechanizmu korbowo-wodzikowego w położeniu przedstawionym na
rysunku, jeśli korba OA obraca się z prędkością ω=2[rad/s]=const.
OA=0,2m; AB=0,6m; α=60˚.

OA

v

OA

A















90

sin

r

v

OA

A



]

/

[

4

,

0

2

,

0

2

s

m

v

A







Kierunek prędkości B jest znany gdyż ogniwo 3 może poruszać się tylko w jeden sposób.

Ad3.

Metoda superpozycji

:

r

r

r

A

B





dt

r

d

dt

r

d

dt

r

d

v

A

B

B







A

A

v

dt

r

d



const

r 

r - zmienia się zwrot i kierunek

r

dt

r

d







r

v

v

A

B









B

A

v

AB

v









BA

A

B

v

v

v





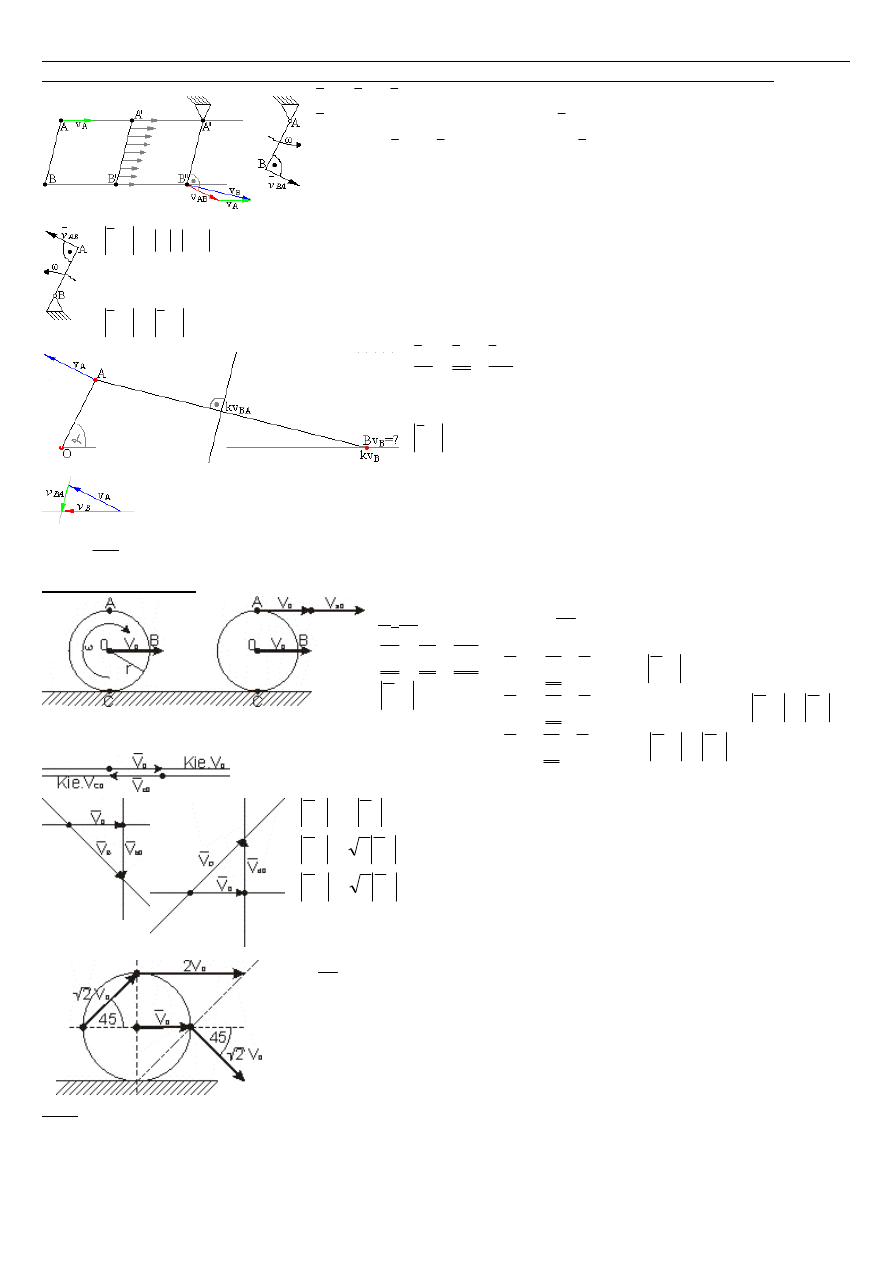
5

Prędkość dowolnego punktu w ruchu płaskim stanowi sumę geometryczną wektora punktu przyjętego
jako biegun oraz wektora prędkości w ruchu obrotowym punktu szukanego względem bieguna.

BA

A

B

v

v

v





BA

v

BA



Kierunek prędkości

BA

v

jest prostopadły do odcinka BA,

a dodani

A

v i

BA

v

daje wartość

B

v .

AB

v

AB







AB

v

AB



ω taka sama

BA

AB

v

v



BA

A

B

v

v

v





v

B

||do prowadnic

BA

v

BA



BA

v

BA

BA







Odkładamy siłę v

A

( znamy ją ) oraz kierunki sił v

B

, i v

BA

– tworzymy plan prędkości z

którego odczytujemy wartości sił nieznanych.

BA

v

BA

BA





Tocząca się tarcza.

V

C

=0

r

V

T

0





0

C

o

C

V

V

V





r

V

T

C







0

kV

C0



C0

0

0

0

2

2

2

V

V

V

V

V

V

D

B

A







r

V

T

0





Ad4.

Metoda chwilowego środka prędkości

. Przemieszczenie ciała w ruchu płaskim można przedstawić

jako obrót dokoła punktu zwanego chwilowym środkiem obrotu.
Chwilowym środkiem obrotu nazywamy w danym położeniu, taki punkt S przekroju dla którego w
danej chwili prędkość liniowa równa jest zero.

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

B

kV

D

kV

V

V

V

V

V

V

V

A

kV

V

V

V

A

V

V

V

V

B

D

B

D

D

A

B

B

T

A

A

A





























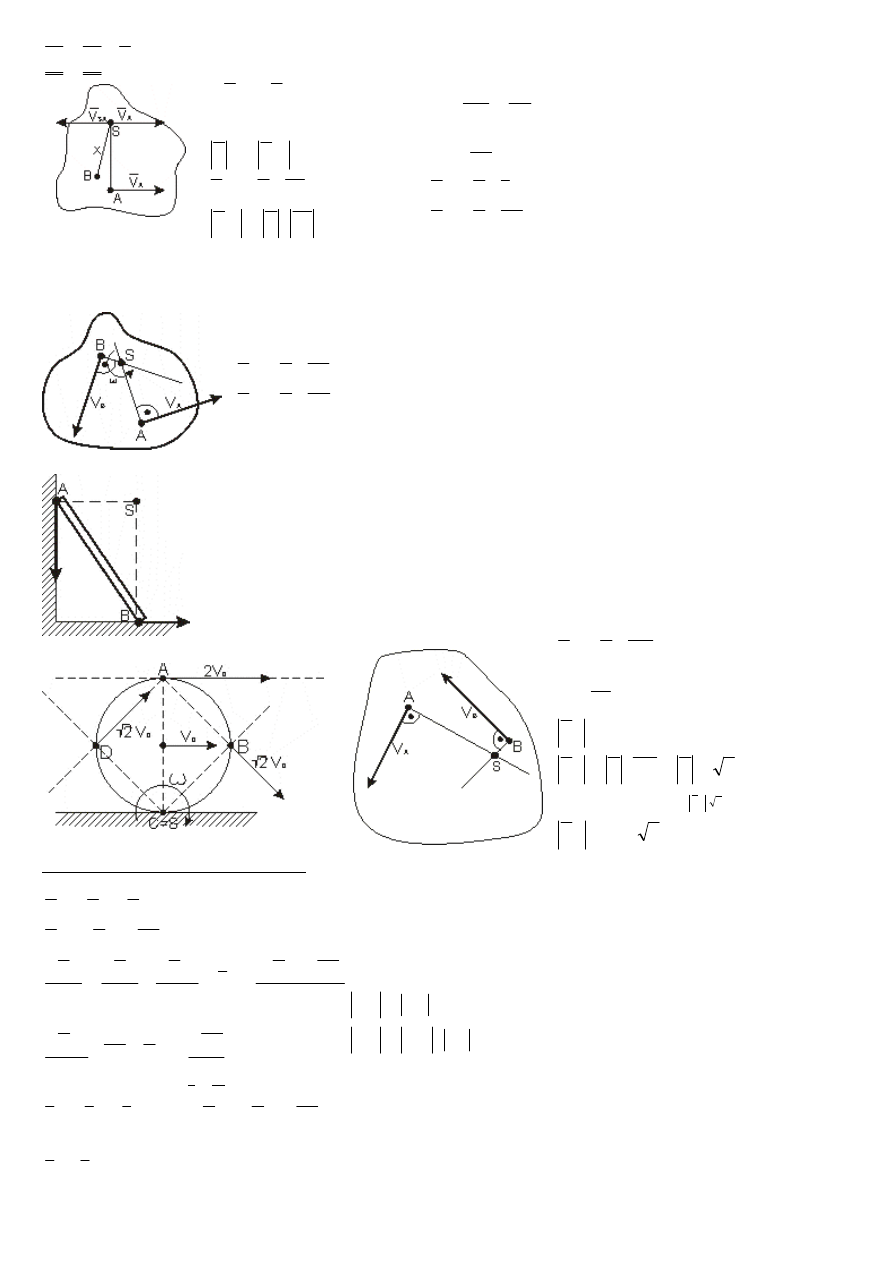
6

SA

A

S

V

V

V





1



















SA

V

SA

V

V

V

SA

V

V

V

SA

SA

SA

A

SA

A

SA





BS

V

x

V

V

SA

SA

V

SA

V

B

B

A

A

SA























W celu wyznaczenia chwilowego środka prędkości wystawiamy prostopadłe do kierunków prędkości
dwóch punktów badanego przekroju poruszającego się ruchem płaskim, punkty przecięcia dają chwilowy
środek prędkości.

AS

V

BS

V

V

S

A

B

S

















0

UWAGA! Może być ułożenie wektorów prędkości dla których niema punktu chwilowego obrotu.

DEFINICJA CENTROIDY:
Ruch płaski możemy rozpatrywać jako wiele następujących po sobie obrotów
chwilowych w około przemieszczającego się ośrodka obrotu. Kolejne położenia
środków w układzie nieruchomym nazywamy cętroidą stałą, zaś w układzie
ruchomym cętroidą ruchomą.

0

0

2V

V

r

V

AC

V

A

A













2

2

2

0

r

V

r

BC

V

D

V

B





























Przyspieszenie w ruchu płaskim.
Metoda super pozycji.











n

BA

T
BA

A

B

a

BA

BA

a

BA

A

B

BA

BA

BA

BA

A

BA

A

a

B

BA

BA

BA

A

B

a

a

a

a

BA

BA

a

a

dt

BA

d

BA

dt

d

dt

BA

d

a

dt

V

d

dt

V

d

dt

V

d

BA

V

V

V

V

n
BA

T
BA

BA

BA

B















































 



 









































BA

a

BA

a

BA

a

BA

a

n

BA

T
BA

BA

n

BA

BA

T
BA

||

2















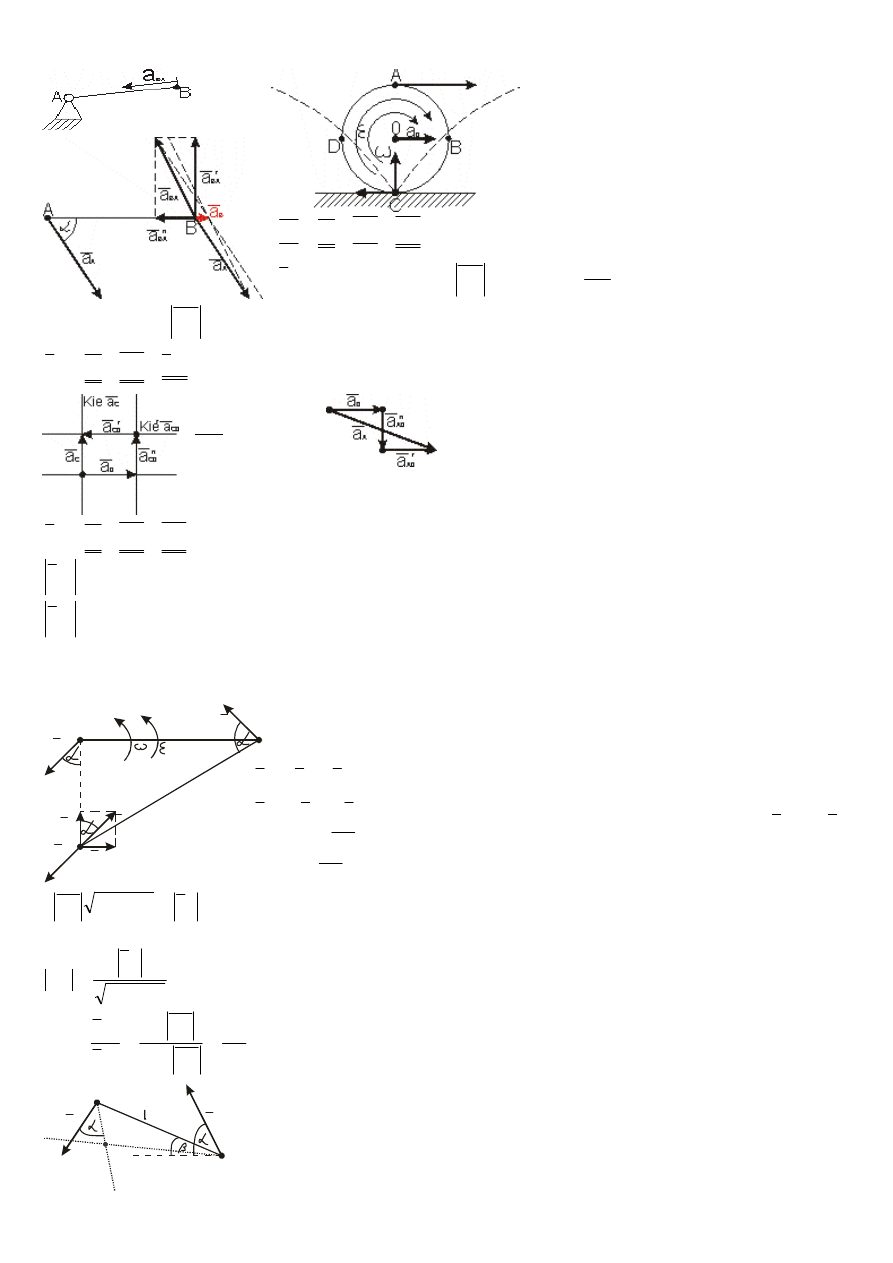
7

BA

0

0

0

0

0

||

2

2

0

2

0

0

0

0

0

0

C

C

v

C

a

C

C

a

a

a

a

a

C

C

n

C

n
C

n

C

T

C

C























 

1

0

0

??

0

0









r

T

C

T

C

C

a

C

a



n

A

T
A

A

a

a

a

a

0

0

0















0

0

0

C

T

C

C

a

n

B

t

B

B

a

a

a

a

0

0

0







0

2

0

B

a

n
B







0

0

B

a

t

B







Chwilowy środek przyspieszeń.

W ruchu płaskim bryły w każdej chwili istnieje punkt , którego przyspieszenie jest równe zero – punkt
ten nazywamy chwilowym środkiem przyspieszeń.

Zakładając, że a

p

=0 przyspieszenie punktu P obliczonego metodą

superpozycji, będzie wynosić:

AP

a

AP

a

a

a

a

a

a

a

t
PA

n

PA

t

PA

n
PA

PA

PA

A

P





















2

a

P

– przyspieszenie chwilowe środka przyśpieszeń:

A

PA

a

a





P

a

AP





2

2





Odległość chwilowego środka prędkości od punktu A wynosi:

2

2



 



P

a

AP

2

2





















AP

AP

a

a

tg

n
PA

t

PA

BP

a

B



Dane: a

A

=2m/s

2+

a

B

=4m/s

2

l=1m β=30˚

Szukane: ε, ω=?

P=?

A

B

P

I

r

I

a

A

I

a

A

B

I

a

I

a

A

I

a

PA

I

n

I

a

PA

I

t

I

a

PA

I

a

A

P

B

I

a

A

B

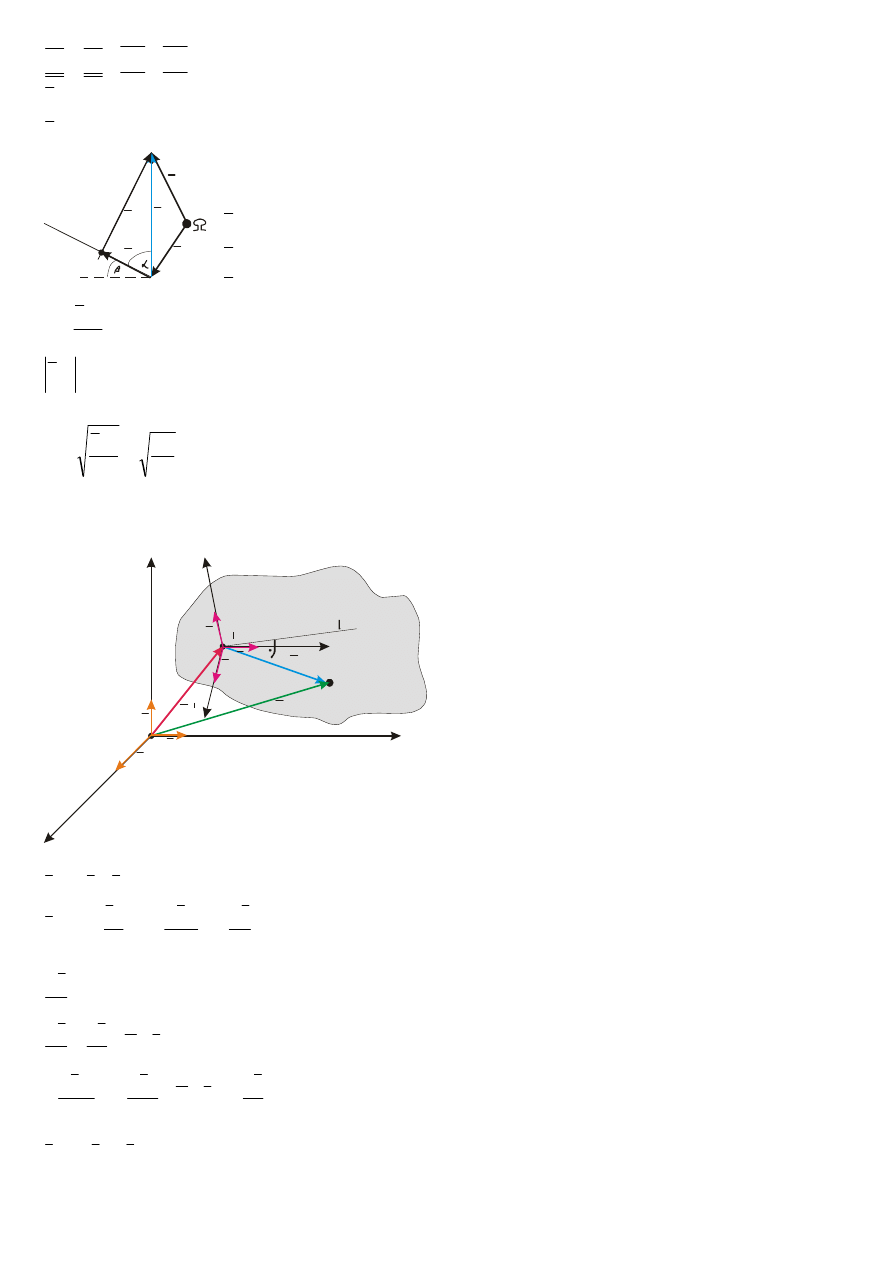
8

t

BA

n

BA

A

B

a

a

a

a







Ba

a

BA

a

t
BA

n
BA



||

2

2

2

/

5

/

5

,

3

/

5

,

3

s

m

a

s

m

a

s

m

a

BA

n
BA

t

BA







BA

a

s

m

BA

a

n

BA

n
BA

t

BA













2

/

5

,

3

s

m

s

m

BA

a

n
BA

/

8

,

1

/

5

,

3

1

5

,

3

2















Ruch punktu bryły sztywnej poruszającej się ruchem złożonym – ruch złozony punktu.

Ruch punktu M względem nieruchomego punktu
odniesienia 0XYZ nazywamy ruchem bezwzględnym.

Ruch punktu M względem ruchomego układu

odniesienia 0’xyz nazywamy ruchem względnym.

Ruch układu ruchomego 0’xyz względem układu nieruchomego 0XYZ nazywamy ruchem

unoszenia.

Prędkość i przyspieszenie w ruchu złożonym.







wzglęzgl

unoszenia

a

bezwzglęez

r

M

M

dt

r

d

dt

r

d

dt

v

v

r

r

r











'

'

0

0

-

dt

r

d

zmienia kierunek bez zmiany wartości





wzglęwzg

v

unoszenia

v

0

a

bezwzglęez

v

t

r

r

dt

r

d

dt

r

d

r

t

r

dt

r

d

M

































w

u

bM

v

v

v





I

a

PA

I

n

P

I

a

PA

I

tP

B

I

a

A

I

a

A

B

I

a

X

Y

Z

X

Z

Y

M

I

r

I

r

M

I

r

0

I

j

I

k

I

i

I

k

1

I

i

1

I

j

1

0

0

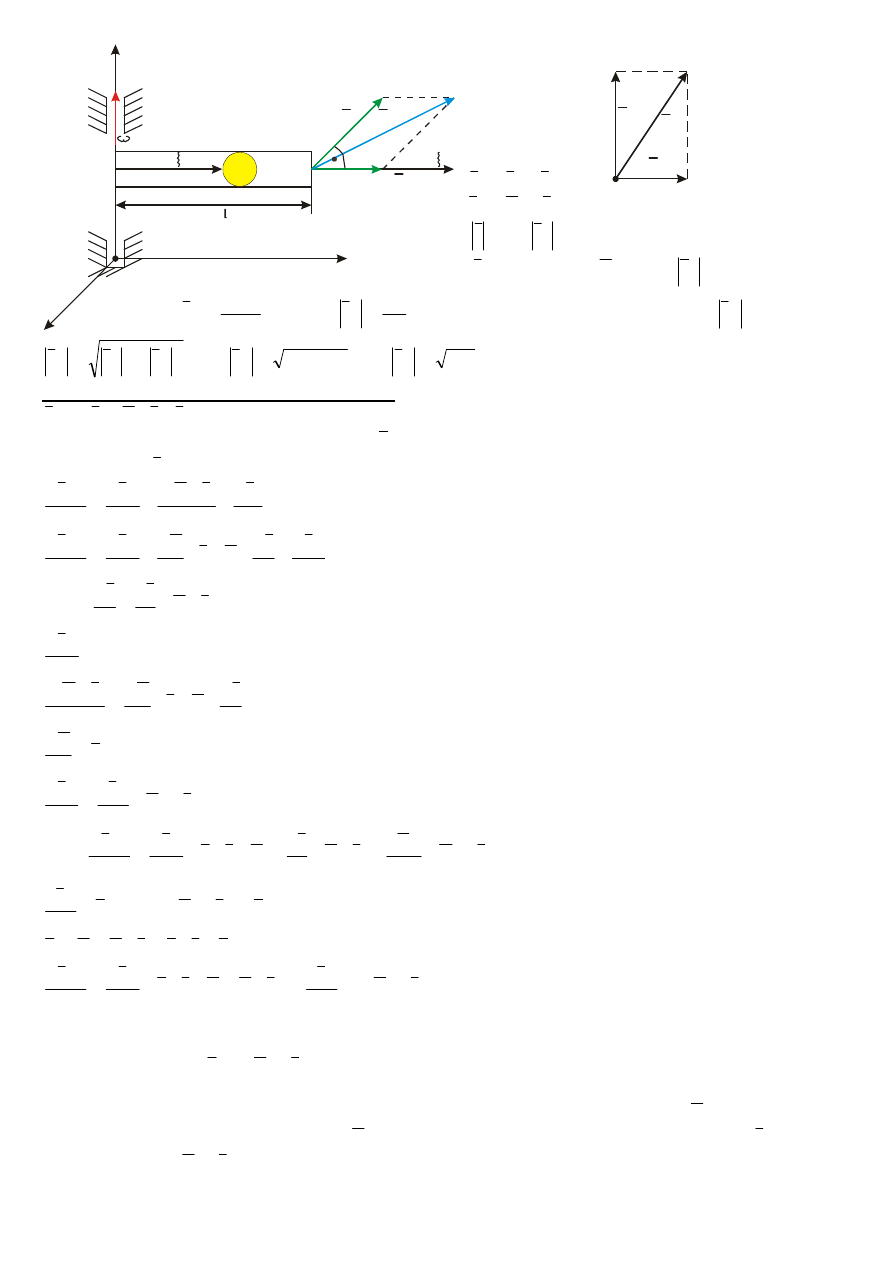
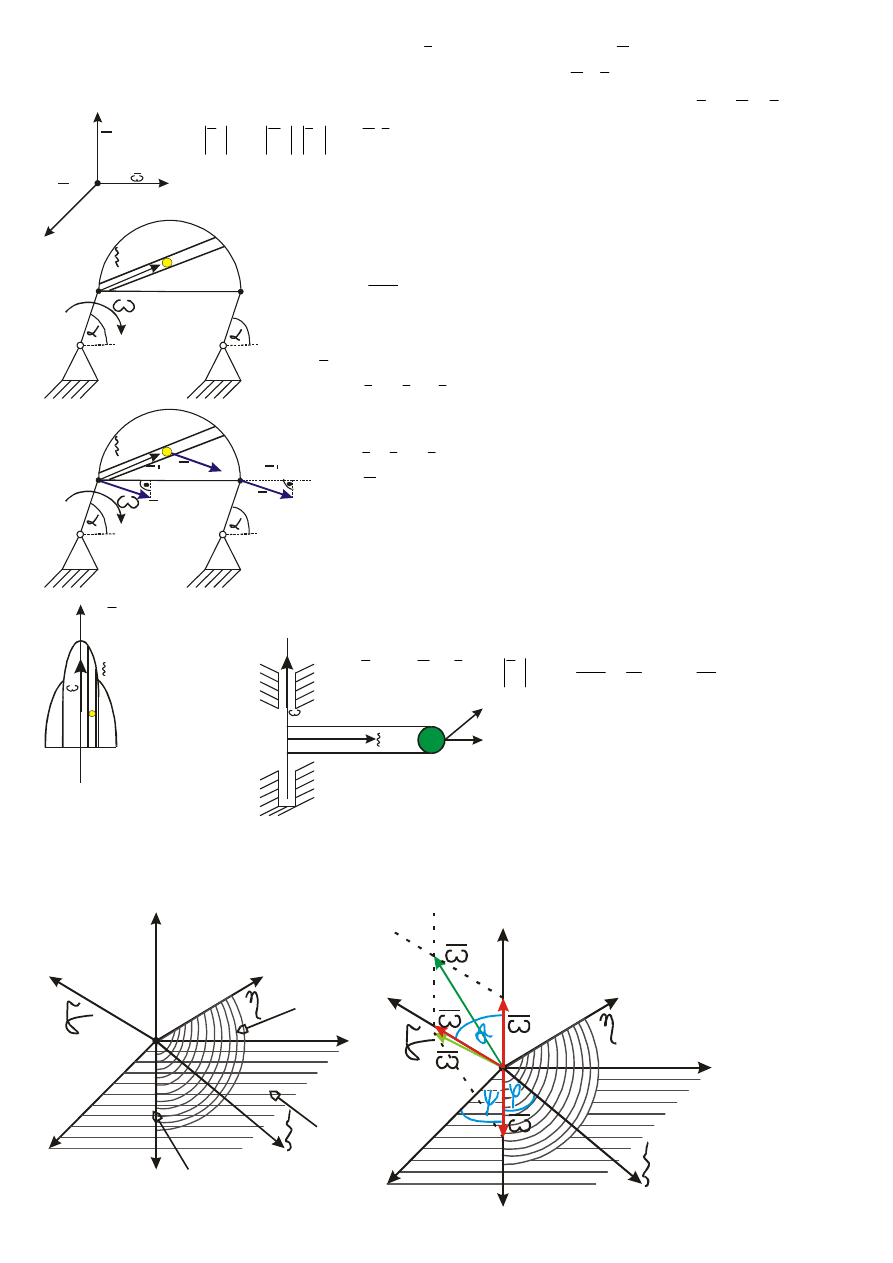
9

ω

u

=2rad/s

ζ(t)=2t

2

[m]

l=8m

Szukane:

V

m

(t

l

)

w

u

b

v

v

v





r

v

u

u









  











90

sin

8

/

2

m

s

rad

v

l

r

u

s

m

y

plaszczyzn

v

u

u

u

/

16

v











 

t

t

v

w









t

t

v

w

4











 

s

t

t

t

2

8

2

2











s

m

v

w

/

8

2

4







2

2

w

u

B

v

v

v





320

64

256







B

B

v

v

Przyspieszenie punktów w ruchu złożonym.

w

bM

r

r

v

v











'

0

Przyspieszenie bezwzględne punktu M=

bM

a

jest równe pochodnej względem czasu prędkości

bezwzględnej

bM

v

tego punktu





dt

v

d

dt

v

d

r

dt

d

dt

v

d

dt

v

d

dt

r

v

d

dt

r

d

dt

v

d

dt

v

d

w

bM

o

bM



























'

'

0

gdzie:

r

t

v

dt

v

d













'

'

0

0

a

dt

v

d







dt

v

d

r

dt

d

dt

r

d























dt

d

w

u

w

w

v

dt

v

dt

v

d











więc:

w

u

w

bM

v

t

V

r

t

v

v

dt

v

d

dt

v

d



















































'

0

w

w

a

dt

v





coriolisa

-

2

c

w

u

a

v 









u

a

r

r

a



















'

0





































coriolisa

wzgledne

unoszenia

0

2

'

a

w

u

a

w

a

bM

v

t

v

r

r

dt

v

d

dt

v

d































Przyspieszenie coriolisa jest podwójnym iloczynem wektorowym prędkości kątowej unoszenia i

prędkości względnej:

w

u

c

v

a







2

Przyspieszenie coriolisa nie występuje czyli jest równe zero, kiedy:

1. Ruchem unoszenia są ruchy: prostoliniowy, harmoniczny, prosty i postępowy:

0



u



2. Gdy wektory prędkości kątowej

 jest równoległy do wektora prędkości względnej

w

v

w

u

v

||



X

Z

Y

I

m

(t)

V

B

V

I

u

V

I

w

Ia

Ia

V

B

V

I

u

V

I

w

10

3. W przypadku kiedy prędkość względna

w

v będzie równa zero

0





, przyspieszenie coriolisa

jest wektorem



do płaszczyzny utworzonej przez wektory

w

u

v

,



.

Zwrot przyspieszenia coriolisa zgodny jest z regułą śruby prawo skrętnej

w

u

c

a

v

i





Wartość:





w

w

u

c

v

v

a

,

sin

2













r=0,2m

α=60˚

s

rad

2





 

2

6t

t 



t=3[s]

?



c

a

BA

A

B

v

v

v





v

A

’=v

B

’

v

A

=v

B

B

A

v

v

v





0



u



Ruch postępowy, a więc przyspieszenie coriolisa jest równe zero.

0



c

a

bo prędkość unoszenia jest równoległa do prędkości

w

u

c

v

a









2

2

32

1

8

2

2

s

m

s

m

s

rad

a

c











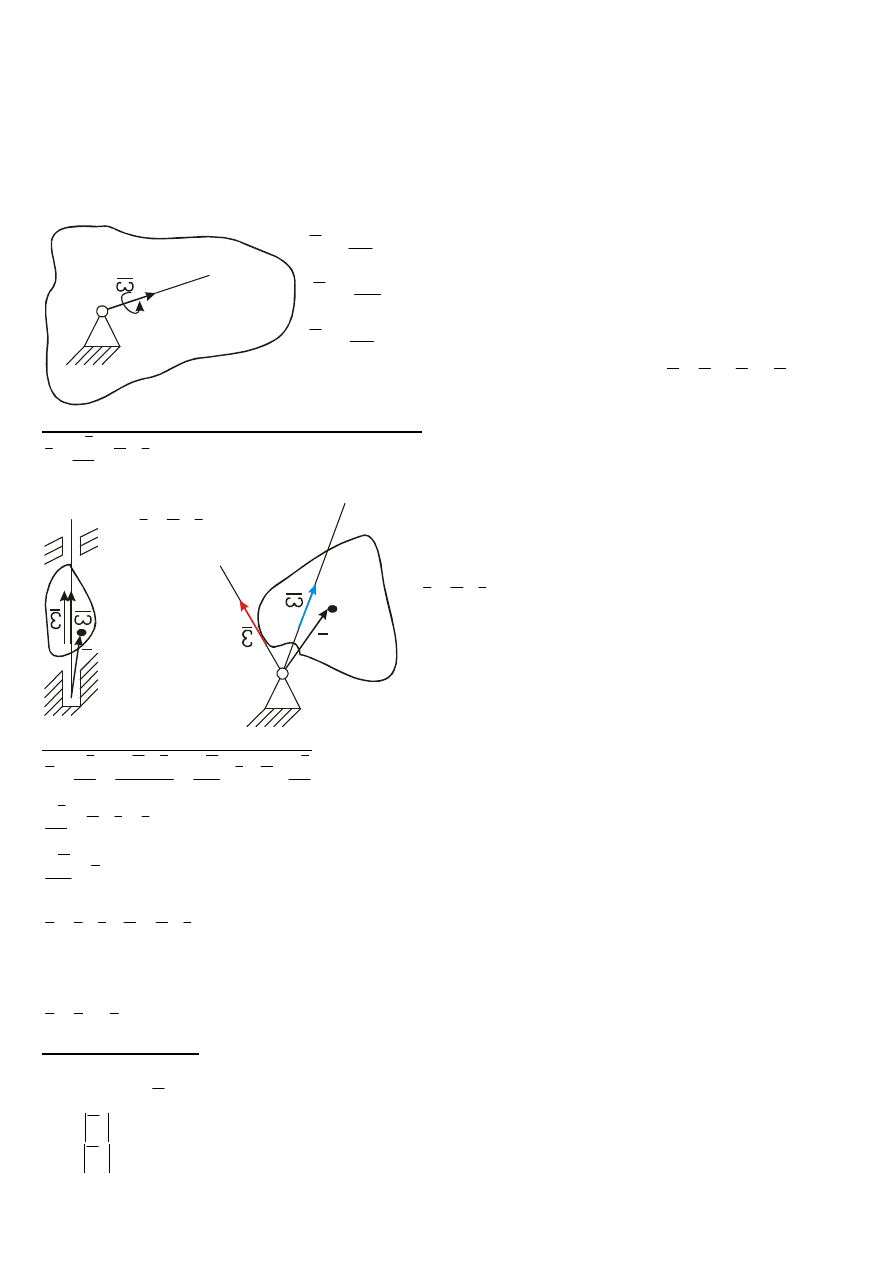
Ruch kulisty –

jest to taki ruch ciała sztywnego podczas którego jeden punkt zwany środkiem ruchu

kulistego jest nieruchomy, zaś torami pozostałych punktów są powierzchnie kuli o środku w punkcie
będącym środkiem ruchu kulistego.
Ruch kulisty opisujemy przy pomocy kątów Eulera.

φ – kąt obrotu własnego

ψ – kąt precesji

 –kąt nutacji

C

I

a

W

I

v

A

B

I

(t)

A

B

I

(t)

A

V

B

V

U

V

A

V

B

V

Z

I

(t)

I

(t)

Z

V

B

I

u

V

X

Y

Z

0

N

Zeta

Teta

Xi

Płaszczyzna
teta - xi

Płaszczyzna
XY

Krawędź przecięcia
płaszczyzn

X

Y

Z

N

Zeta

Teta

Xi

0

1

2

3

2

1

3

12

11

Kąty Eulera:
Podczas ruchu ciała sztywnego wartości kątów obrotu własnego, precesji, nutacji zmieniają się w czasie:

 

t

f

1





 

t

f

2





 

t

f

3





Aby jednocześnie określić ruch należy podać trzy równania.
Ruch ciała sztywnego w ruchu kulistym ma trzy stopnie swobody.

Prędkość kątowa w ruchu kulistym.

dt

d







1

- prędkość kątowa obrotu własnego

dt

d



2



- prędkość kątowa precesji

dt

d







3

- prędkość kątowa nutacji

Prędkość kątowa wyrażona jest jako suma geometryczna:

3

1















Prędkość dowolnego punktu w ruchu kulistym.

r

dt

v

d

v









OBROTOWY KULISTY

ω - chwilowa

Przyspieszenie w ruchu kulistym.





dt

r

d

r

dt

d

dt

r

d

dt

v

d

a





















v

r

dt

v

d















dt

d

, stąd:



















D

a

v

a

r

r

a

















0

a

o

– przyspieszenie obrotowe,

a

D

– przyspieszenie do osiowe.

D

o

a

a

a





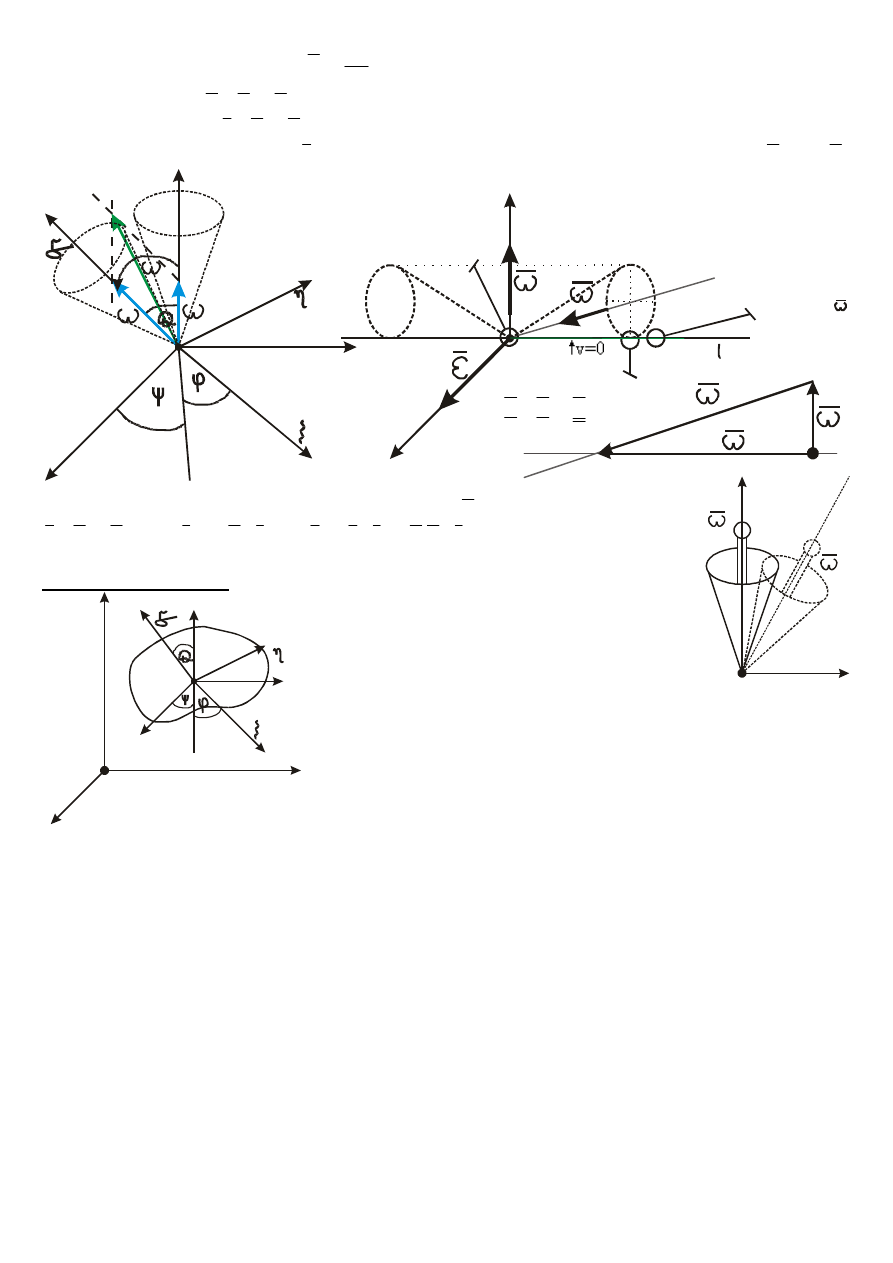
Precesja regularna: kąt nutacji jest stały, a prędkość nutacji równa się zero – wartości prędkości obrotu
własnego i precesji są stałe.























.

.

0

.

2

1

3

const

const

const









0

I

l

I

r

I

l=const.

r

v







I

r

r

v







12

Prędkość kątowa precesji wynosi:

0

3





dt

d





Suma geometryczna:

2

1











Przyspieszenie kątowe:











2

Wektor przyspieszenia kątowego

 jest prostopadły do płaszczyzny wyznaczonej wektorami

1

 oraz  .

1.

Szukamy

chwilowej

osi obrotu

dla

danego

położenia.

Prędkość

punktów leżących na chwilowej osi

obrotu jest równa 0.

2. Szukamy punktów nieruchomych ( 1, 2 ) jest to oś

 .











2

A

r

v

AC



















m

V

An

m

u

r

r

a















Ruch bryły swobodnej.

Położenie bryły sztywnej w ruchu dowolnym będzie

jednoznacznie określone jeżeli w danej chwili

czasowej będą znane współrzędne ruchomego układu
x

0

(t), y

0

(t), z

0

(t) oraz kąty

 

t



,

 

t



,

 

t



.

X

Y

Z

1

2

12

X

Z

Y

1

2

0

1

2

Chwilowa oś obrotu,
na niej znajduje się

2

1

2

1











1

2

X

Y

Z

Z

X

Y

0

1

0

13

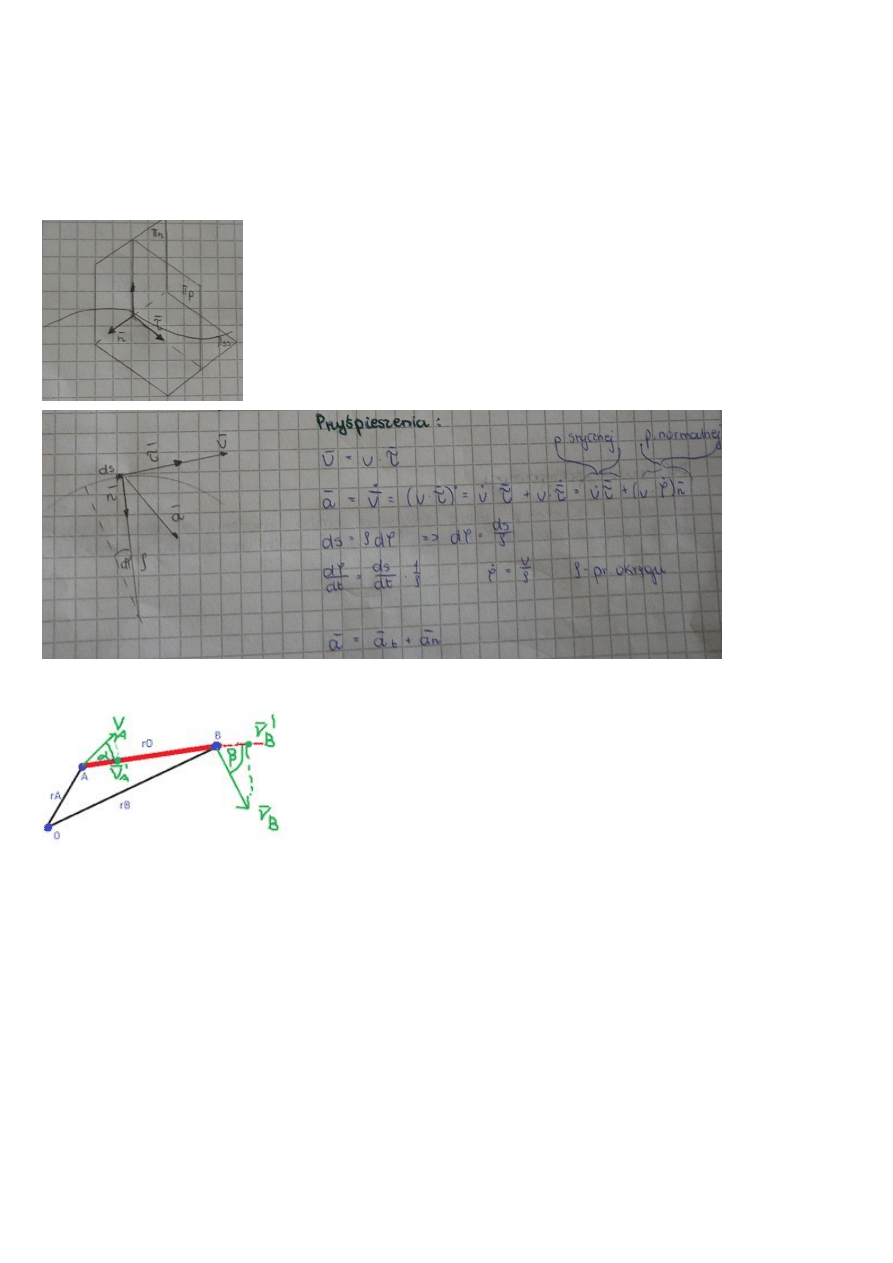
Naturalny układ współrzędnych

Podczas ruchu punktu po dowolnym torze możemy poprowadzić do toru
płaszczyznę ściśle styczną(π

ss

), płaszczyznę normalną (π

n

) i płaszczyznę prostującą

(π

p

) w miejscu w którym znajduje się aktualnie rozważany punkt. Krawędzie

przecięcia się płaszczyzn są osiami: styczną normalną główną i binormalną.

Trójścian FRENETA

Twierdzenie o ruchu prostej:

rzuty prędkości dwóch dowolnych punktów ciała sztywnego na prostą łączącą te

punkty są sobie równe.

(WEKTOROWO)

r0•r0=|r0|

2

=const

(rB-rA)

2

-r0

2

=0 po zróżniczkowaniu względem czasu i przyjęciu oznaczeń:

rB+rA=r, (rA)’=VA, (rB)’=VB daje rVB=rVA czyli 
rVAcos(r,VA)=rVBcos(r,VB)  VAcos(r,VA)=VBcos(r,VB)

Aksoidy

Aksoida ruchoma jest to miejsce geometryczne chwilowych osi obrotu w układzie ruchomym.
Aksoida nieruchoma jest to miejsce geometryczne chwilowych osi obrotu w układzie nieruchomym