Mariusz Pluciński
Informatyka, gr. 1
Projekt ppp09c - drzewo czerwono-czarne
Drzewo czerwono-czarne - sprawozdanie
Opis algorytmu
Drzewo czerwono-czarne jest w istocie rozszerzeniem struktury zwykłego drzewa binarnego przez dodanie do niego tzw. własności czerwono-czarnych. Zmodyfikowane w ten sposób drzewo charakteryzuje się zautomatyzowanym równoważeniem po każdej operacji wstawiania/usuwania elementów. Dzięki temu że drzewo jest cały czas zrównoważone, operacja wyszukiwania przebiega znacznie szybciej niż w zwykłym, niezrównoważonym drzewie.
Struktura binarnego drzewa poszukiwań
Binarne drzewo poszukiwań, w stosunku do zwykłych drzew, posiada kilka dodatkowych założeń:
Stopień każdego wierzchołka jest nie większy od 3
Oznacza to, że każdy wierzchołek ma co najwyżej dwóch synów.
Wyróżnia się lewego i prawego syna, przy czym lewy syn zawsze ma wartość klucza nie większą od wartości klucza swojego rodzica, a prawy syn wartość nie mniejszą od wartości klucza swojego rodzica.
Przy czym w programie prezentacyjnym przyjęto założenie o unikalności kluczy, w celu uproszczenia implementacji.
Istotną cechą binarnego drzewa poszukiwań jest jego zrównoważenie. Drzewo jest zrównoważone, gdy dla każdego węzła różnica w wysokości jego lewego i prawego poddrzewa wynosi co najwyżej 1. Cecha ta jest ważna, gdyż operacja wyszukiwania (jak również dodawania i usuwania) elementów wykazuje najbardziej optymalne działanie w przypadku drzew zrównoważonych. Samo binarne drzewo poszukiwań nie przewiduje jednak automatycznego równoważenia, tak więc najczęściej wykorzystuje się jego rozszerzenia, wprowadzające takie możliwości. Jednym z takich rozszerzeń jest właśnie drzewo czerwono-czarne.
Własności czerwono-czarne
Drzewo czerwono-czarne rozszerza strukturę zwykłego binarnego drzewa poszukiwań przez wprowadzenie kilku dodatkowych założeń, gwarantujących względne zrównoważenie drzewa:
Każdemu z węzłów zostaje przypisany dodatkowy atrybut - kolor - o dwóch dopuszczalnych wartościach: czerwony lub czarny.
Korzeń drzewa jest zawsze czarny
Każdy pusty liść jest traktowany jako czarny
Wszyscy synowie każdego czerwonego węzła są czarni
Każda ścieżka prowadząca z korzenia do dowolnego liścia zawiera tę samą liczbę czarnych węzłów (inaczej: czarna wysokość każdego węzła od korzenia jest taka sama). Właśnie ta właściwość gwarantuje utrzymanie zrównoważenia w drzewie.
Operacja rotacji
Ważną rolę w implementacji operacji wstawiania i usuwania elementów w drzewie czerwono-czarnym (jak również w wielu innych algorytmach równoważenia drzew) pełni operacją rotacji. Wyróżnić można operację rotacji w lewo lub w prawo.
Rotacja węzła x w lewo polega na zamianie jego pozycji w drzewie z pozycją jego prawego syna - y. Węzeł x staje się wówczas lewym synem węzła y, węzeł y zajmuje natomiast pozycję węzła x w relacji z jego dawnym rodzicem. Zależność pomiędzy węzłem x i jego lewym synem nie ulega zmianie, podobnie jak zależność pomiędzy węzłem y a jego prawym synem. Natomiast lewy syn węzła y staje się prawym synem węzła x, przenosząc ze sobą całe poddrzewo.
Rotacja węzła w prawo przebiega analogicznie, z tym że wymianie pozycji podlega węzeł x oraz jego lewy syn. Zależności i operację są wówczas symetryczne do tych opisanych wyżej.
Rotacja w lewo węzła jest wykonalna jeżeli posiada on prawego syna. Analogicznie rotacja w prawo jest wykonalna, jeżeli węzeł posiada lewego syna.
Procedura wyszukiwania
Operacja wyszukiwania w drzewie czerwono-czarnym przebiega w sposób identyczny co w zwykłym drzewie binarnym.
Należy rekurencyjnie przyrównywać poszukiwaną wartość klucza do wartości klucza danego węzła. Jeżeli są równe, to szukana wartość została właśnie znaleziona.
Jeżeli wartość poszukiwanego klucza jest mniejsza od wartości klucza w sprawdzanym węźle, to należy sprawdzić czy dany węzeł ma lewego syna. Jeżeli nie ma, to żaden węzeł w drzewie nie posiada takiej wartości klucza. Jeżeli ma, należy przejść do tego syna i na nim wykonać sprawdzanie rekurencyjne.
Analogicznie, jeżeli wartość poszukiwanego klucza jest większa od wartości klucza w sprawdzanym węźle, należy sprawdzić czy sprawdzany węzeł posiada prawego syna. Jeżeli nie ma, to żaden węzeł w drzewie nie posiada takiej wartości klucza. Jeżeli ma, należy przejść do tego syna i na nim wykonać sprawdzanie rekurencyjne.
Algorytm rozpoczyna się od sprawdzenia korzenia, następnie przechodzi on rekurencyjnie po niższych gałęziach, kończąc się zgodnie z podanymi warunkami. Możliwe jest również skonstruowanie wersji iteracyjnej algorytmu.
Procedura wstawiania
Procedura wstawiania elementu do drzewa czerwono-czarnego jest rozbudowana w stosunku do procedury wstawiania w zwykłym drzewie binarnym.
Wstawianie wartości do zwykłego drzewa binarnego jest operacją zbliżoną do operacji wyszukiwania, z taką zmianą, że w przypadku stwierdzenia nie istnienia danej wartości w drzewie zostaje ona wstawiona właśnie w to miejsce gdzie stwierdzono jej brak. Natomiast postępowanie w przypadku znalezienia klucza o takiej wartości jaką chcemy wstawić zależy od tego czy przyjęto założenie o unikalności kluczy w drzewie czy nie.
Nowo wstawiony węzeł jest zawsze kolorowany na czerwono. Potem następuje operacja przywrócenia własności czerwono-czarnych.
Algorytm przywracania właściwości czerwono-czarnych rozpoczyna się ze wskaźnikiem x ustawionym na nowo wstawiony węzeł. Na początek sprawdza się, czy rodzic węzła x jest czerwony (gdyż tylko wtedy własności drzewa zostały zaburzone). Jeżeli nie, drzewo uznaje się za zrównoważone i kończy pracę algorytmu wstawiania.
Dalszy tok postępowania zależy od wystąpienia jednego z sześciu warunków, związanych z kolorami węzłów leżących na pobliskich nowo wstawionemu gałęziach. Zazwyczaj rozpatruje się jedynie trzy warunki, ponieważ druga trójka jest ich ich symetrycznym odbiciem, a przynależność do drugiej z nich zmienia jedynie kierunek wykonywanych rotacji na przeciwny. Poniższe opisy odnoszą się do przypadku gdy ojciec węzła x jest lewym synem swojego ojca (dziadka węzła x):
Brat ojca węzła x jest czerwony
W takiej sytuacji należy pokolorować zarówno ojca węzła x jak i jego brata na czarno. Następnie ustawić wskaźnik x na ojca ojca węzła x (tzn. dziadka) i rozpocząć algorytm przywracania własności na tym węźle.
Brat ojca węzła x jest czarny, a x jest prawym synem swojego ojca
Ten przypadek zazwyczaj sprowadza się do przypadku trzeciego, poprzez wykonanie na ojcu węzła x obrotu w lewo.
Brat ojca węzła x jest czarny, a x jest lewym synem swojego ojca
W takiej sytuacji należy pokolorować ojca węzła x na czarno, dziadka węzła x na czerwono, a następnie wykonać na dziadku węzła x obrotu w prawo.
Powyższe przypadki (wraz z ich trzema symetrycznymi wersjami) są w pełni wystarczające, aby zapewnić utrzymanie właściwości czerwono-czarnych przez drzewo, a zgodnie z założeniem 5. również utrzymanie zrównoważenia przez drzewo.
Procedura usuwania
Procedura usuwania węzła z drzewa czerwono-czarnego, podobnie jak pozostałe operacje na tym drzewie, stanowi rozszerzenie tej operacji dla zwykłych drzew binarnych.
Postępowanie podczas usuwania węzła w drzewie binarnych zależy od tego, ilu ma on synów:
żadnego - nie są wymagane żadne dodatkowe operacje, węzeł może zostać usunięty bezpośrednio
jednego - podstawić syna usuwanego węzła w miejsce relacji rodzica usuwanego węzła z usuwanego węzła
dwóch - należy znaleźć następnik usuwanego węzła (najbardziej lewy element w jego prawym poddrzewie), następnie wstawić następnika w miejsce usuwanego węzła.
Następnie, o ile usuwany węzeł był czarny, należy wykonać algorytm przywracania własności czerwono-czarnych, za wskaźnik początkowy przyjmując jedynego syna usuwanego węzła.
Opis programu
Program prezentacyjny przedstawia strukturę drzewa czerwono-czarnego w formie graficznej. Węzły zawierają przypisane im wartości liczbowe oraz kolor. Zachowana jest również hierarchia węzłów.
Programem steruje się przy pomocy poleceń wpisywanych z klawiatury. Rozpoznawany jest następujący zestaw poleceń:
insert x - (za x podstawić należy wartość liczbową z zakresu 1-255) - wstawienie elementu o wartości klucza x do drzewa.
random x - (za x podstawić należy wartość liczbową z zakresu 1-255) - wstawienie x elementów (każdy o losowej wartości) do drzewa.
find x - (za x podstawić należy wartość liczbową z zakresu 1-255) - odszukanie elementu o wartości klucza x w drzewie.
delete x - (za x podstawić należy wartość liczbową z zakresu 1-255) - usunięcie elementu o wartości klucza x z drzewa.
exit - koniec pracy programu.
Przedstawienie działania algorytmu dla przykładowych danych
W drzewie czerwono-czarnym operacją o niewątpliwie największym stopniu komplikacji jest wstawianie elementów. Poniższy opis odnosi się do tego właśnie algorytmu.
Rozważmy proste drzewo z kilkoma węzłami i zachowanymi własnościami czerwono-czarnymi.
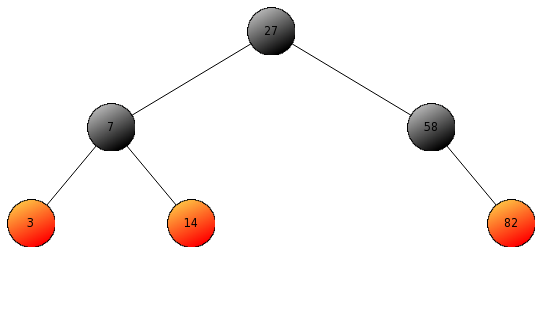
Dla tak przygotowanego drzewa prześledźmy krok po kroku procedurę wstawiania elementu o wartości 89.
Na początek, umieszczamy węzeł 89 za pomocą standardowej procedury dla drzew binarnych. Węzeł 89 staje się wówczas prawym synem węzła 82. Nowy węzeł kolorujemy zawsze na czerwono.
Następnie stwierdzamy, że zarówno nowy węzeł (89) jak i jego rodzic (82) mają kolor czerwony. Należy więc dokonać operacji przywrócenia własności czerwono-czarnych.
Obrany przypadek zależy od koloru brata ojca. W opisywanym wypadku węzeł 82 nie ma brata, zakładamy więc obecność w tym miejscu czarnego wartownika. Jako że 89 jest prawym synem 82, zachodzi przypadek nr 3. Zgodnie z procedurą obsługi tego przypadku, kolorujemy ojca (82) na czarno, dziadka (58) na czerwono, a następnie wykonujemy na dziadku obrót w lewo.
Ostatecznie, drzewo po wykonaniu operacji wygląda następująco:
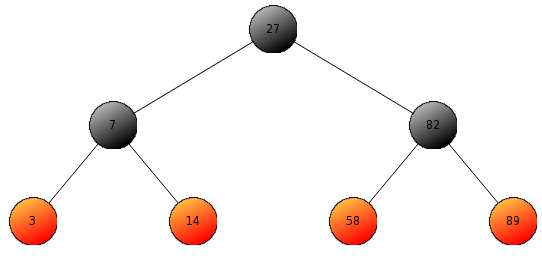
Wyszukiwarka
Podobne podstrony:
drzewo czerwono czarne
drzewo czerwono czarne
200 Stendhal, Czerwone i czarne
Stendhal - Czerwone i czarne, opracowania oświecenie romantyzm
czerwone i czarne t 1 stendhal E4RR6HVQCAV3VIQ4US3LHOMPJAE2BZG53DIR32A
czerwone i czarne
Stendhal - Czerwone i czarne - streszczenie, kulturoznawstwo, semestr II
czerwone i czarne t 2 stendhal TQYMTU5ZMUYJ4DY2T6WPZMUEFT25ULBNYTHLRMQ
11 Stendhal Czerwone i czarne
CZERWONE I CZARNE
STENDHAL CZERWONE I CZARNE T2
Stendhal Czerwone i czarne 01 treść
Stendahl Czerwone i czarne (t 1)
Stendhal Czerwone i czarne tom 1
Stendhal Czerwone i Czarne 1
Stendahl, Czerwone i czarne1
Stendhal Czerwone i Czarne t 1
Julian Sorel z powieści Stendhala Czerwone i czarne a bohaterowie romantyczni
czerwone i czarne stendhal
więcej podobnych podstron