Laboratorium Technik Cyfrowych nr 3

Projektowanie układów logicznych jest ważnym i zarazem trudnym zagadnieniem. Możemy je wykonać np. w następujące sposoby:

• Bezpośrednio wg tabeli prawdy.

• Minimalizując funkcję algebraicznie.

• Metodą tabeli Karnaugha zaznaczając grupy jedynek.

• Metodą tabeli Karnaugha zaznaczając grupy zer.

• Dowolną metodą z powyższych, przedstawiając rozwiązanie za pomocą jednego rodzaju bramek.

Podstawową rzeczą zatem jest stworzenie tabeli prawdy, z której korzystamy niezależnie od wybranego przez nas sposobu. Pierwszy sposób jest oczywiście najprostszym i zarazem najgorszym rozwiązaniem. Minimalizacja funkcji algebraicznie nie jest łatwa jednakże, jeśli biegle korzystamy z praw i twierdzeń algebry Boole`a, może być bardzo szybką metodą.

Bramka logiczna - element konstrukcyjny maszyn i mechanizmów (dziś zazwyczaj: układ scalony, choć podobne funkcje można zrealizować również za pomocą innych rozwiązań technicznych, np. hydrauliki czy pneumatyki), realizujący fizycznie pewną prostą funkcję logiczną, której argumenty (zmienne logiczne) oraz sama funkcja mogą przybierać jedną z dwóch wartości, np. 0 lub 1 (zob. algebra Boole'a).

Podstawowymi elementami logicznymi, stosowanymi powszechnie w budowie układów logicznych, są elementy realizujące funkcje logiczne: sumy (alternatywy), iloczynu (koniunkcji) i negacji. Są to odpowiednio bramki OR, AND i NOT. Za pomocą dwóch takich bramek (np. OR i NOT lub AND i NOT) można zbudować układ, realizujący dowolną funkcję logiczną.

Bramki NAND (negacja koniunkcji), oraz NOR (negacja sumy logicznej) nazywa się funkcjonalnie pełnymi ponieważ przy ich użyciu (tzn. samych NAND lub samych NOR) można zbudować układ realizujący dowolną funkcję logiczną. Dowolną bramkę logiczną można też skonstruować za pomocą pary bramek, np. za pomocą OR i NOT lub AND i NOT. Układy takie nazywamy układami zupełnymi.

Bramkę logiczną XOR często wykorzystujemy w układach arytmetyki takich jak sumatory lub subtraktory.

1. Przedstawienie zagadnienia.

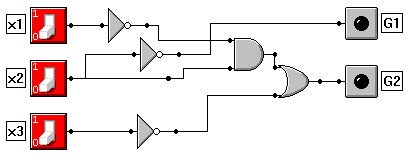
Laboratorium nr 3 polega na zaprojektowaniu układu logicznego obsługującego sytuację przedstawioną za pomocą poniższego schematu.

x₁, x₂, x₃ są czujnikami które informują układ o tym czy odpowiednia dla każdego z nich temperatura została osiągnięta, odpowiednio do otrzymanych danych układ włącza lub wyłącza grzałki G1 i G2.
W sprawozdaniu przyjąłem, że czujnik x1 (i odpowiednio pozostałe) zaczyna emitować sygnał „1” gdy temperatura T jest większa lub równa od T₁. Podobnie grzałka jest włączona gdy otrzymuje sygnał „1” i wyłączona gdy otrzymuje „0”. Przyjąłem również założenie, że moc grzewcza G₁ jest większa od G₂.

2. Analiza problemu.

W przypadku zadań 3, 4, 5 mamy zbudować zwykłe układy logiczne. Jednak w przypadku zadania 6, musimy zbudować układ uwzględniający możliwość awarii czujników, co powoduje, że trzeba ponownie przeanalizować tabelę prawdy i w miejsca stanów nieustalonych grzejników podać konkretne wartości logiczne „1” lub „0” w zależności od informacji dostarczanych przez czujniki.
Awarię możemy wykryć jedynie gdy czujnik wyższej temperatury zwraca „1” a niższej „0”. Ten sposób jednak nie wykrywa sytuacji w której czujnik x1 uległ awarii i stale zwraca wartość „0”. W takiej sytuacji nie jesteśmy w stanie wykryć awarii i zabezpieczyć układu przed przegrzaniem. Przyjmujemy założenie, że maksymalnie 1 czujnik może ulec awarii oraz, że w przypadku niejednoznacznym ważniejsze jest by nie przekroczyć mocy grzewczej układu (zakładamy, że temperatura przyjmuje wartość wyższą).

3. Zbudować wariant nieoptymalny (wg tabeli prawdy).

x3	x2	x1	G1	G2
0	0	0	1	1
0	0	1	-	-
0	1	0	-	-
0	1	1	-	-
1	0	0	1	0
1	0	1	-	-
1	1	0	0	1
1	1	1	0	0

G₁= ~x₁ * ~x₂ * ~x₃ + x₃ * ~x₂ * ~x₁
G₂= ~x₁ * ~x₂ * ~x₃ + x₃ * x₂ * ~x₁




4. Zbudować wariant minimalny najprostszy układ kombinacyjny (wg tabeli Karnaugha).

G1
x3 \ x1, x2	00		01		11	10
0	1		-		-	-
1	1		0		0	-
G2
x1, x2 \ x3	0	1
00	1	0
01	-	1
11	-	0
10	-	-

G₁ = ~x₂

G₂ = ~x₃ + ~x₁ * x₂




5. Zbudować wariant minimalny na jednym typie bramek.

G₁ = ~x₂
G₂ = ~x₃ + ~x₁ * x₂
A NOR A ~A
G₁ = x₂ NOR x₂
G₂= (x₃ NOR x₃) + [(x₁ NOR x₁) AND x₂]
A OR B (A NOR B) NOR (A NOR B)
A AND B (A NOR A) NOR (B NOR B)
G₂ = [(x₃ NOR x₃) NOR (x₁ NOR (x₂ NOR x₂))] NOR [(x₃ NOR x₃) NOR (x₁ NOR (x₂ NOR x₂))]




6. Zbudować układ uwzględniający możliwość awarii czujników.

Przyjąć założenie, że może być uszkodzony jeden czujnik, może wtedy pokazywać trwale stan 0 albo 1.

Awaria jednego z czujników rozpoznawana jest wtedy, gdy czujnik wyższej temperatury pokazuje, że temperatura została osiągnięta, a czujnik niższej pokazuje, że ta nie została osiągnięta.

Grzałki powinny być sterowane jak najdokładniej wg zasad pod rysunkiem, w sytuacji niejednoznacznej ważniejsze jest aby nie przekroczyć mocy grzania przy danej temperaturze.

W każdym przypadku awarii powinna się zaświecić lampka sygnalizująca stan awarii.

x3	x2	x1		Awaria			G1		G2
0	0	0		0			1		1
0	0	1		1			1		1
0	1	0		1			0		1
0	1	1		1			0		0
1	0	0		0			1		0
1	0	1		1			0		0
1	1	0		0			0		1
1	1	1		0			0		0
- miejsca wykrywalnych awarii
G1
x3 \ x1, x2			00		01	11		10
0			1		0	0		1
1			1		0	0		0

G2
x3 \ x1, x2	00	01	11	10
0	1	1	0	1
1	0	1	0	0

Lampka awarii
x3 \ x1, x2	00	01	11	10
0	0	1	1	1
1	0	0	0	1


G₁ = ~x₂ * (~x₁ + ~x₃)
G₁ = ~x₂ * ~(x₁ * x₃)
G₁ = ~ (x₂ + (x₁ * x₃))
G₁ = x₂ NOR (x₁ * x₃)

G₂ = (~x₁ + ~x₂) * (~x₃ + ~x₁) * (~x₃ + x₂)
G₂ = (x₁ NAND x₂) * (x₁ NAND x₃) * (~x₃ + x₂)

Awaria = x₂ * ~x₃ + x₁ * ~x₃ + x₁ * ~x₂
Awaria = ~x₃ * (x₂ + x₁) + x₁ * ~x₂




7. Wnioski

• Układ zbudowany w oparciu o tabelę prawdy przekazuje do grzałek sygnał „0” podczas gdy w tabeli wartość jest nieokreślona.

• Układ zbudowany zarówno w oparciu o tabelę prawdy jak i tabelę Karnaugha nie sprawdza się w przypadku wystąpienia awarii, gdyż w pierwszym wypadku wyłącza wszystkie grzałki, a w drugim w zależności od sposobu grupowania włączy je (grupowanie „1”) lub wyłączy (grupowanie „0”).

• Sposób wykrywania awarii nie wykrywa wszystkich możliwych awarii. Stany czujników
  (x₃ = 1, x₂ = 1, x₁ =1), (1,1,0), (1,0,0), (0,0,0) mimo iż potencjalnie mogą zawierać awarię takowej nigdy nie zgłoszą. Dodatkowo założenie, że maksymalnie 1 czujnik może być w danym momencie uszkodzony wyklucza pewne możliwości interpretacji stanów np. (0,1,1) mógłby być zinterpretowany jako uszkodzenie x₂ i x₃, jednak przy obecnym założeniu wskazuje jednoznacznie na uszkodzenie x₁.

• Pomimo swej niedoskonałości sposób wykrywania uszkodzeń czujników jest stosunkowo dobrym rozwiązaniem, gdyż nie wymaga innych dodatkowych czujników, w związku z czym jest najtańszą metodą wykrywania pojedynczych awarii czujników systemu grzewczego.
  
  

Damian Pawlik
WFMiIS
grupa 21

~A + ~B ~(A * B)

~A * ~B ~(A + B)
~(A + B) A NOR B

---