Sprawozdanie ,,C2”

	ĆWICZENIE ,,C2” POMIAR CIEPŁA WŁAŚCIWEGO POWIETRZA METODĄ ROZŁADOWANIA KONDESATORA.
FIZYKA I ROK	OCENA Z KOLOKWIUM	OCENA ZE SPRAWOZDANIA	OCENA KOŃCOWA

I.WSTĘP TEORETYCZNY

Równanie stanu gazu doskonałego:

Przemianę izotermiczną (T = const) opisuje prawo Boyle'a i Mariotte'a:

Dla ustalonej porcji gazu iloczyn ciśnienia i objętości jest w ustalonej temperaturze wielkością stałą

p₁V₁ = p₂V₂ = const

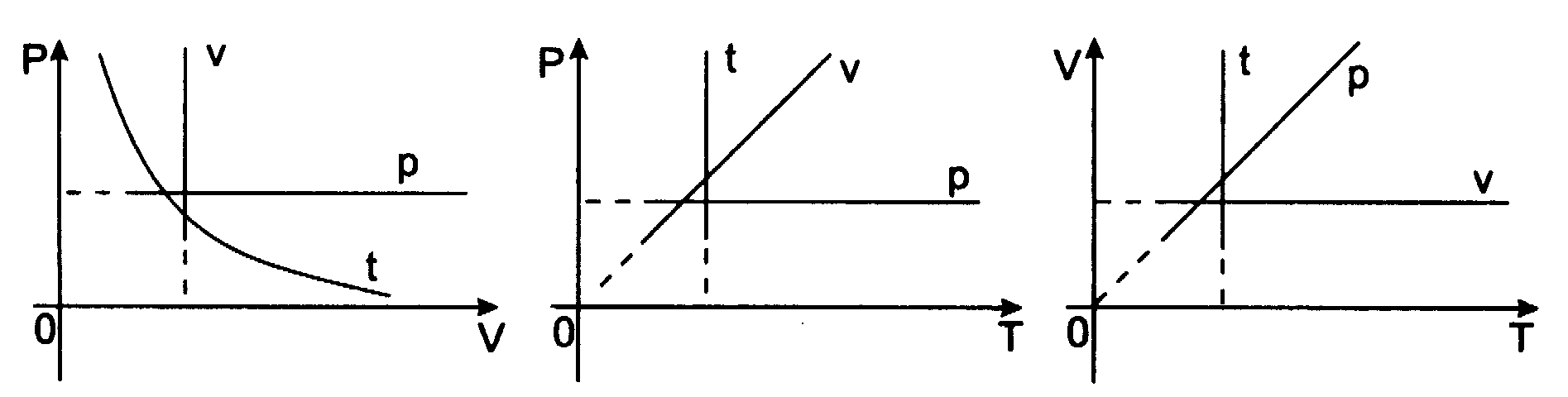
Przemianę izobaryczną opisuje prawo Gay - Lussaca:

Dla ustalonej porcji gazu pod stałym ciśnieniem wzrost temperatury o 1^oC powoduje wzrost objętości gazu o
objętości, jaką zajmował gaz w temperaturze 0^oC

V - objętość gazu w temperaturze t (^oC) V₀ - objętość gazu w temperaturze 0^oC

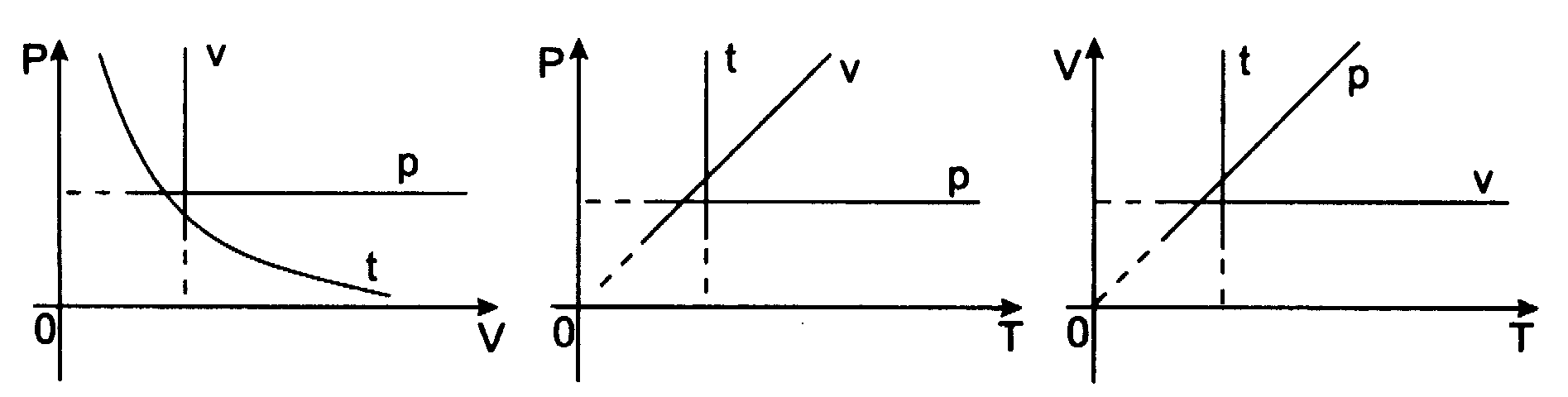
Przemianę izochoryczną (V = const) opisuje prawo Charlesa:

Dla ustalonej porcji gazu w stałej objętości wzrost temperatury o 1^oC powoduje wzrost ciśnienia gazu o
ciśnienia, jakie miał gaz w temperaturze 0^oC

p - ciśnienie w temperaturze t

p₀ - ciśnienie w temperaturze 0^oC

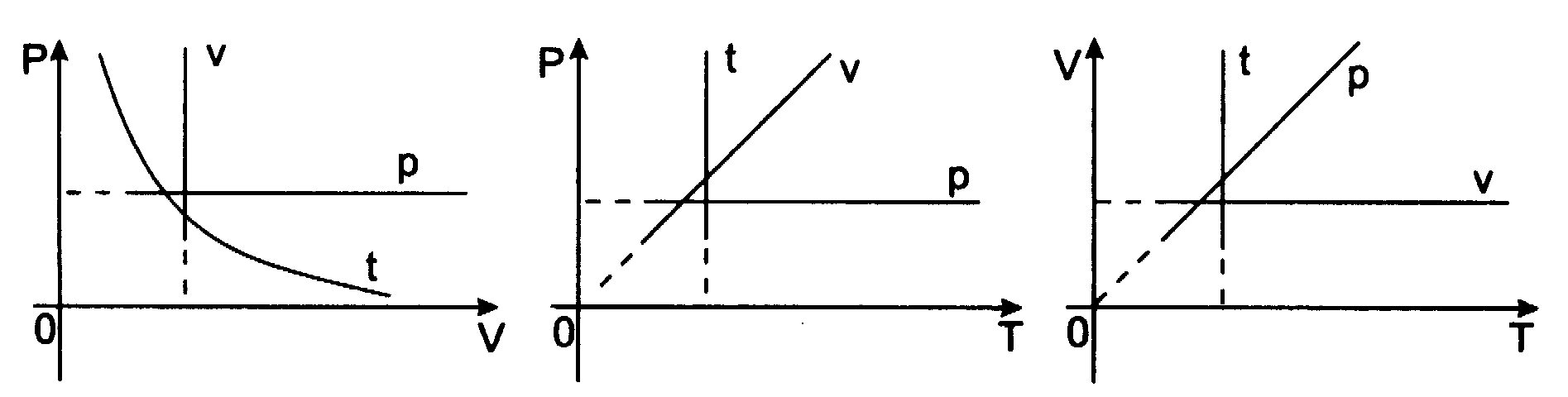
Prawo Gay - Lussaca i Charlesa uzyskują postać, gdy temperaturę podajemy w skali Kelwina:

T - odpowiada temperaturze t

T₀ - odpowiada temperaturze 0^oC

Pierwsza zasada termodynamiki - zmiana energii wewnętrznej ciała równa jest algebraicznej sumie pracy wykonanej nad ciałem przez siły zewnętrzne i ciepła wymienionego z otoczeniem

ΔE_k = W + Q

ΔE_k - zmiana energii wewnętrznej

W - wykonana praca

Q - ciepło wymienione z otoczeniem

Zasada ta stwierdza, że dostarczone ciepło dQ może być wykorzystane na wzrost energii wewnętrznej dE i wykonanie przez gaz pracy dW.

dQ = dE + dW = dE + pdW

Podczas ogrzewania ciała z zachowaniem stałej objętości, ciepło musi być dostarczone jedynie na wywołanie przyrostu energii wewnętrznej, związanego ze wzrostem temperatury, natomiast podczas ogrzewania pod stałym ciśnieniem gaz się rozszerza i wykonuje prace (dV≠0), co wymaga dostarczenia większej ilości energii potrzebnej zarówno na wzrost energii wewnętrznej, jak i wykonanie pracy.

Ciepło molowe - to ilość ciepła potrzebna do ogrzania 1 mola substancji o 1 Kelwin. Ciepło molowe przy stałej objętości wnosi:

n - liczba moli

i - liczba stopni swobody

Średnia energia cząsteczki gazu jest proporcjonalna do temperatury:

i - liczba stopni swobody

k - stała Boltzmana

Dla gazu jednoatomowego i = 3 (do opisu tego gazu wystarczy znajomość trzech składowych prędkości). Dla gazu dwuatomowego, i = 5, gdyż ruch takiej cząsteczki opisują trzy składowe prędkości ruchu środka masy i dwie składowe związane z ruchem obrotowym.

Dla gazu dwuatomowego energia wewnętrzna wyniesie:

N - liczba Avogadro

Nk = R - stała gazowa

Dlatego też ciepło molowe przy stałej objętości wyniesie:

Zasada ekwipartycji energii - gdy liczba punktów jest bardzo duża i obowiązuje mechanika Newtonowska, wówczas wszystkie wyrazy tj.
, mają taką samą wartość i ta wartość zależy wyłącznie od temperatury.

Innymi słowy dostępna energia zależy wyłącznie 0od temperatury i rozkłada się w równych porcjach na wszystkie sposoby, w jakie może ją absorbować cząsteczka. Każdy z takich sposobów absorbcji energii nazywany stopniami swobody.

Kondensatorem - nazywamy taki układ przewodników, w którym obecność jednego wpływa na obecność drugiego przewodnika. Tworzące go przewodniki nazywamy okładkami kondensatora.

Pojemnością kondensatora - nazywamy stosunek zgromadzonego na nim ładunku Q do różnicy potencjałów między jego okładkami. Wielkość ta jest stała dla danego kondensatora, jeśli znajdujące się w pobliżu naładowane lub uziemione przewodniki nie zmieniają położenia. Wielkość ta informuje nas, jaki ładunek wprowadzić na okładki, by napięcie między nimi wynosiło 1V. Jednostką pojemności w układzie ,,SI” jest
(jeden Farad)

W układzie pomiarowym następuje rozładowanie kondensatora przez opornik (który, w tym przypadku stanowi spirala), znajdujący się w naczyniu z gazem (naczynie Dewara). Wzrost temperatury spirali powoduje wzrost temperatury gazu w wyniku czego, gaz zwiększa swoją objętość i ciśnienie. Wzrost ciśnienia mierzymy za pomocą manometru rtęciowego. Przy dużej objętości naczynia w stosunku do objętości manometru przemianę możemy uznać za przemianę izochoryczną, zgodnie z zależnością:

U - napięcie

C - pojemność kondensatora

Przyrosty ciśnienia zależą liniowo do U², zaś współczynnik kierunkowy (nachylenia) tej prostej:

pozwala obliczyć C_V:

II.CZĘŚĆ PRAKTYCZNA

Wartości ustalone:

V = 0,5 · 10^-3 m³

C = 5000
1000μF = 0,005F

T = 296 K

p = 735 · 10^-3 m · 9,81
· 13609
= 98060,76

Wyniki otrzymane podczas przeprowadzania doświadczenia zestawiłem w tabeli nr. 1:

Tab. 1

L.p	U [V]	U^2 - xi [V]	p [mm H2O]	∆p - yi [Pa]	xiyi	xi^2	yi^2
1	12	144	0,0065	66,217	953,248	20736	4384,70
										0,007
			2					14	196	0,0115	110,3625	21631,05	38416	12179,90
										0,011
			3					16	256	0,0017	167,751	42944,256	65536	28140,40
										0,0172
			4					18	324	0,024	240,345	77871,78	104976	577657,72
										0,025
			5					20	400	0,029	289,395	115758	160000	83749,45
										0,030
			6					22	484	0,037	367,875	178051,5	234256	135332,02
										0,038
			7					24	576	0,044	441,45	254275,2	331776	194878,1
										0,046
			8					26	676	0,055	549,36	371367,36	456976	301796,41
										0,057
			9					28	784	0,067	664,6275	521067,96	614656	441729,71
										0,0685
∑		3840		2897,383	1583920,354	2027328	1779848,40

Obliczam współczynnik a i b:

Wyznaczam odchylenie standardowe od wartości a:

Wyznaczam odchylenie standardowe od wartości b:

Wyznaczam prostą teoretyczną:

y = ax + b → y = 0,89x - 60

x = 0 ; y = - 60

x = 790 ; y = 643,1

Wyznaczam proste y₁, y₂:

y₁ = (a + S_a)x + (b + S_b) y₂ = (a - S_a)x + (b - S_b)

x = 0 ; y₁ = 12151,85 x = 0 ; y₂ = -12271,185

x = 790 ; y₁ = 13036,65 x = 790 ; y₂ = 12270,525

Obliczam ciepło właściwe ze wzoru:

Wyznaczam niepewność ciepła właściwego metodą różniczki zupełnej:

Wyznaczam niepewność procentową pomiaru ciepła właściwego:

Wnioski:

Celem doświadczenia było wyznaczenie ciepła właściwego powietrza metodą rozładowania kondensatora. Błędy obliczeniowe powstały na skutek niedokładności przyrządów pomiarowych. Pomimo to wyniki są obarczone dość małą niepewnością ok. 3,31%.

1

---