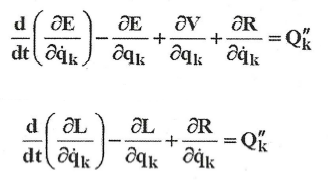
RÓWNANIA LAGRANGE'A II-GO RODZAJU: algorytmiczny sposób uzyskiwania równań różniczkowych modelujących zachowanie się układów dynamicznych. k=1,…,s Gdzie: E - energia kinetyczna, V - energia potencjalna, L- potencjał kinetyczny (funkcja Lagrange'a), q_k - współrzędne uogólnione, Q_k'' - siły uogólnione (niepotencjalne), R - funkcja Ripley'a.
REGULATORY PROPORCJONALNE P: z(t)=k*e(t)+z₀, gdzie k - wsp. proporcjonalności [zakres proporcjonalności to przedział (0,1/k)], e(t) - uchyb, z₀ - wstępna wartość wielkości nastawiającej. Charakterystykę czasową regulatora otrzymuje się nadając uchybowi postać skoku jednostkowego. Transmitancja operatorowa: K(s)=k.
REGULATORY CAŁKUJĄCE I: wartość wielkości nastawiającej zmienia się z prędkością proporcjonalną do uchybu. Z(t)=
T_i - czas działania całkującego (czas zdwojenia), z₀ - wstępna wartość wielkości nastawiającej. Transmitancja: K(s) =
Odpowiedź skokowa: z(t)=

REGULATOR PROPORCJONALNO-RÓŻNICZKUJĄCY PD: wartość wielkości wyjściowej jest proporcjonalna do prędkości zmian wielkości wejściowej. Zależność funkcyjna między wielkością nastawiającą a uchybem: z(t) = kT_d
, K(s)=k[T_is+1]
REGULATORY PROPORCJONALNO-CAŁKUJĄCE PI - zależność funkcyjna między wielkością nastawiającą a uchybem: z(t)=
Transmitancja operatorowa: K(s) = k[
Charakterystyka czasowa: z(t)=k[

REGULATORY PID - utrzymuje wartość wyjściową na określonym poziomie, zwanym wartością zadaną. Realizuje algorytm: z(t)=k_p[T_d

Transmitancja idealna: K(s)=k[
Transmitancja rzeczywista: K(s)=k[
Aby z regulatora PID zrobić regulator: -P, należy ustawić Ti=∞ -PD, należy ustawić Ti=∞ -Pi, należy ustawić Td=0
Analiza częstotliwościowa- zajmuje się przenoszeniem przez układ funkcji harmonicznie zmiennych. Umożliwia ona określenie częstotliwości składowych zawartych w przebiegu czasowym funkcji. Jeżeli f jest okresowa to korzystając z przekształcenia Fouriera można określi wartości amplitud czest podstawowej i harmonicznej.
Przekształcenie Laplacea- przekształcenie które opisuje związek miedzy funkcja czasu zwana oryginałem a odpowiadającą funkcja zespolona zwana transformata zmiennej zespolonej L[x(t)]=X(s)=∫0→∞ x(t)e^-st dt. Własności: -liniowość (przekształcenie spelnia zasade superpozycji) L[a*f1+b*f2]=a*F1+b*F2 -transformata splotu, tw. Borela L[f1*f2]=F1*F2 -tw o zmienie skali(podobieństwie) L[f(^t_k)]=k*F(s*k) -tw o przesunieciu rzeczywistym L[f(t-a)*l(t-a)]= e^-asF(s) -tw o przesunieciu zespolonym L[e^-λtf(t)]=F(s+λ) -tw o transformacie pochodnej funkcji czasu -tw o transf calki oznaczonej funkcji czasu od 0 do t -tw i różniczkowaniu transf L[t*f]=-dF/ds -tw o całkowaniu transf L[f(t)/t]= ∫s→∞ F(λ) d λ -tw odnoszące się do splotu dwóch funkcji Warunki istnienia transf: f(t)=0 dla t<0, f(t) okreslona jednowartosciowa i posiada pochodna przy t>0,
Transmitancją operatorową G(s) jednowymiarowego układu liniowego stacjonarnego nazywamy wielkość określoną jako stosunek transformaty odpowiedzi Y(s) do transformaty wymuszenia U(s) tego układu przy zerowych warunkach początkowych. Jest częstotliwościowym modelem układu (określonym w dziedzinie s). Określa ogólne własności stacjonarnego układu liniowego.
Transmitancją widmową G(jω) liniowego układu stacjonarnego nazywamy wielkość określoną jako stosunek wartości zespolonej składowej wymuszonej Y(jω) wywołanej wymuszeniem sinusoidalnym do wartości zespolonej tego wymuszenia U(jω)
Charakterystyka statyczna: funkcja określająca zależność wielkości wyjściowej y_s elementu lub układu, od wielkości wejściowej x_s w stanie ustalonym (y_s x_s=const), czyli Y_s=f_s(x_s)
Charakterystyka dynamiczna czasowa: przebieg w czasie odpowiedzi układu dynamicznego y(t) na zadane wymuszenie x(t) (naczęściej standardowe wymuszenie funkcją Heaviside'a).
Charakterystyka częstotliwościowa: charakterystyka opisująca sygnał wyjściowy układu w zależności od amplitudy i częstotliwości sinusoidalnie zmiennego sygnału wejściowego. W przypadkach liniowych, stacjonarnych układów dynamicznych charakterystyka częstotliwościowa jest jednoznacznie określona przez tzw. „transmitancję widmową” układu.
Kryterium stabilności Hurwitza oparte jest na wyznacznikach utworzonych ze współczynników równania charakterystycznego. -badamy współczynniki równania charakterystycznego układu a0sn+ a1sn-1+…+ an-1s+ an=0 -tworzymy wyznaczniki ze współczynników równania charakterystycznego, Jeżeli wszystkie współczynniki a0…an i wszystkie wyznaczniki A1…An są dodatnie to części rzeczywiste pierwiastków rozpatrywanego równania są ujemne i układ jest asymptotycznie stabilny.
Kryterium Michajłowa Oparte jest na analizie krzywej (hodografu Michajłowa) wektora określonego równaniem charakterystycznym układu regulacji (mianownikiem transmitancji przyrównanym do 0) do którego podstawiamy s=jω. Krzywe przedstawiające miejsce geometryczne punktów końców wektorów przy zmianie ω od 0 do ∞ nazywa się hodografem Michajłowa. Układ jest stabilny jeżeli przy ω rosnącym od 0 do +∞ hodograf M. przebiega przeciwnie do ruchu wskazówek zegara od punktu należącego do osi Re; kolejno przez „n” ćwiartek płaszczyzny zmiennych zespolonych (I, II, III, IV) gdzie n jest rzędem równania charakterystycznego.
Kryterium Nyquista opiera się na odwzorowaniu płaszczyzny zespolonej poprzez funkcje zmiennej zespolonej. Ponieważ krzywa odwzorowania jest charakterystyką częstotliwościową układu otwartego (bez sprz. zwr.) może ona posłużyć do badanie układu zamkniętego. Wyraża się: Jeżeli pkt (-1;0) znajduje się na zewnątrz charakterystyki układu otwartego to układ zamknięty jest stabilny. Podstawiamy za s=jω; otrzymamy charakterystykę częstotliwościową. Układ jest stabilny bo (-1;0) jest poza wykresem
Sterowanie- oddziaływanie za pomocą urządzenia sterującego na dany proces fizyczny (obiekt sterowania) aby osiągnąć określony cel Układ sterowania- zespol wspopracujacych urzadzen realizujących zadany proces fizyczny i jego sterowanie. W skł ukł sterowania wchodzi zawsze obiekt sterowania(regulacji) oraz urządzenie sterujące (sterownik lub regulator). Element ukł automatyki- każde urządzenie lub jego czesc występujące w układzie automatycznej regulacji w którym można wyodrębnić sygnaly wejść i wyjściowe( pomiarowe, wzmacniające, sumacyjne i nastawcze)
Sterowanie w ukł otwartym(zamkniętym-ukl automatycznej regulacji)- proces streowania przebiega bez (z) śledzenia (pomiaru) stanu wielkośći sterowanej i bez (z) przekazywanie informacji o stanie tej wielkości (poprzez układ sprzężenia zwrotngo) do urządzenia sterującego.|| Na urządzenie sterujące oddziałują wielkości sterowane w obiekcie (występuje sprzężenie zwrotne). W takim przypadku urządzenie sterujące nazywa się regulatorem. Regulator dokonuje pomiaru różnicy e między wartością zadaną wielkości regulowanej w, a wartością wielkości regulowanej y w dowolnej chwili czasu, a następnie na tej podstawie oddziałuje na człon nastawczy obiektu, przeciwdziałając wpływowi zakłócenia z, czyli zmniejszając uchyb (błąd) regulacji e.Cechy: zamknięta pętla oddzialywan elementow tworzących układ, jednobieżność przepływu sygnalu w torze oddzialywan, ujemnie sprzężenie zwrotne w torze oddzialywan, stała gotowość układu do działania. Ponadto układ charakteryzuje: osiągalność, sterowalność, stabilizowalność, odtwarzalność, obserwowalność, wykrywalność.

Zmienna sterowana- wielkość lub warunek który jest mierzony i sterowany.
Zmienna sterująca- wlk lub war który jest zmieniany przez sterownik tak aby osiagnac wartość zmiennej sterowanej.
Zakłócenie- sygnał który wywiera niekorzystny wpływ na wartość sygnalu wejściowego. Generowane wewnątrz jest nazywane wewnętrznym, a zewnętrzne jest generowane poza systemem i stanowi sygnał wejściowy.
Regulacja automatyczna- proces kompensacji wpływow wielkości zaklucajacych na przebieg realizowanego procesu fizykalnego w taki sposób, aby wartości wielkości regulowanych jak najmniej roznily się od wartości pożądanych.
Obiekt regulacji- podukład układu regulacji w którym dokonuje się regulacji jednej lub wielu wielkości fizycznych.
Błąd(uchyb odchyłka) regulacji- różnica miedzy bieżącą wartością zadana wielkosci regulowanej w(t), a rzeczywista wartością y(t). e(t)=w(t)-y(t)
Regulator- podukł układadu regulacji który dokonuje: pomiaru wartości wlk regulowanej, porównania z wartoscia zadana, przetworzenia sygnału roznicy wielkości zadanej i regulowanej na sygnał nastawczy(sterujący) kompensujący wpływ zaklucen. W wyniku czego wartość wlk regulowanej jest (z zalozonym odchyleniem) rowna wartości zadanej.
Sygnał- dowolna wielkość fizyczna wystepujaca w procesie sterowanie lub automatycznej regulacji za pomocą której sa przekazywane informacje. Charakteryzuje się treścią fizyczna sygnału(wielkość fizyczna która jest nośnikiem informacji no ciśnienie natężenie prądu przepływu) oraz parametrem informacji(wartość wielkości fizycznej).
Informacja-każdy czynnik zwiększający wiedze o otaczajacej rzeczywistości, zmniejszający niepewność działania.
Sygnał analogowy- taki sygnal którego wartości wlk fizycznej jednoznacznie i w sposób ciagly odwzorowywane sa na wartości wlk fiz będącej treścią fizyczna sygnału(czyli na parametr informacji). Sygnał analogowy może przyjmować dowolna wartość z ciągłego przedzialu ograniczonego zakresem zmienności. Jego wart mogą być określone w każdej chwili, dzięki funkcji matematycznej opisującej dany sygnal.
Sygnał dyskretny- charakteryzuje się okreslona liczna skonczoncyh wartości parametry informacji. (próbkowane kwantowe kodowane(cyfrowe))
Sygnał próbkowany- powstaje przes pobranie parametru informacji i przyjecie zalozenia ze pobrana wartość reprezentuje sygnał próbkowany w zadanym przedziale, wynikającym z narzuconej czestotliwosci(gęstości) próbkowania.
Sygnał kwantowy- powstaje poprzez pomiar przyrostu parametru informacji i przyjecie zalozenia o przyrostowej reprezentacji sygnału kwantowego w zadanym przedziale.
Sygnał cyfrowy- dziedzina i zbior wartości da dyskretne. Znaczenie tego terminu może odnosić się do wlk pierwotnie ciągłej i analogowej, która została sprobkowana i skwantowana.
Węzeł sumacyny- wezel ukl automatyki utworzony przez człon sumacyjny posiadający dwa wejście i jedno wyjście, wielkości wejściowe nie ulegaja zmianie, jedynie dodaja się do siebie algebraicznie.
Węzeł zaczepowy(rozgałęziony)- takie rozgałęzienie w torze przepływu sygnalu, do którego nie stosuje się regul dodawania ani odejmowania.
Sprzężenie zwrotne- połącznie umozliwiajace przepływ sygnalu reprezentującego wielkość wyjsciowa do wezla sumacyjnego celem porównania jej z sygnalem reprezentującym wartość wielkości zadanej i wykonanie oddziaływania na urządzenie nastawsze na drodze sygnalu wejściowego do obiektu.
Sterowanie ręczne- gdy sygaly sterujące procesem sa wytwarzane przez urządzenie sterujące w wyniku oddzialywam wymuszeń wymuszonych bezpośrednio aktywnoscia człowieka.
Sterowanie automatyczne- gdy sygnaly sterujące procesem sa wytrwarzane przez urządzenie serujace w wyniku oddzialywan wymuszeń przez celowo dobrane srodki techniczne wchodzące w skład urządzenia sterującego. UKŁAD REGULACJI STAŁOWARTOŚCIOWEJ - Taki układ regulacji, którego algorytm działania realizuje utrzymanie wielkości regulowanej na stałym poziomie. W przypadku układu regulacji stałowartościowej wartość wielkości zadanej w nie ulega zmianom podczas procesu regulacji.
Ukł reg programowej- algorytm działania realizuje zmianę wielkości regulowanej zgodnie z programem założonym z góry. Wartość wielkości zadanej jest znaną funkcją czasu w=f(t).
Ukł reg nadążnej (śledzący)- algorytm działania realizuje zmianę wielkości regulowanej zgodnie ze zmieniającą się w czasie nieznaną z góry funkcją wielkości zadanej w(t), kształtowaną przez czynniki spoza układu regulacji. Zmiany wielkości regulowanej y w układzie nadążają za zmianami wielkości zadanej w, zwanej w tym przypadku wartością wiodącą.
Ukl reg ekstremalnej- algorytm działania realizuje stale ekstremalny poziom wielkości regulowanej, niezależnie od zmieniającej się wartości wielkości zakłócającej.
Serwomechanizm - Techniczna realizacja układu regulacji nadążnej (układu śledzącego), w którym wielkość wyjściowa jest reprezentowana sygnałem mechanicznej współrzędnej położenia (kątem obrotu lub przesunięciem). Ważną cecha takich układów jest fakt, że modele matematyczne poszczególnych elementów układu są znane, a ich parametry nie zmieniają się wraz ze zmianą sygnału zakłóceń.
Ukł reg adaptacyjnej- algorytm sterowania ulega zmianie, realizując pożądane działanie układu, mimo zmian własności obiektu sterowania oraz zmian oddziaływań zewnętrznych.
Ukł rozgrywający-główna cechą zasady działania jest formułowanie sygnałów sterujących na podstawie pewnej gry, czyli porównania zbioru możliwych rozwiązań i dokonywania wyboru w każdej operacji sterowania.
Liniowy ukł sterowania-model matematyczny ma postać liniowych równań różniczkowych, całkowych, różniczkowo-różnicowych bądź operatorowych.
Nieliniowy- model matematyczny ma postać nieliniowych równań różniczkowych, całkowych, różniczkowo-różnicowych bądź operatorowych.
Dyskretny- można opisać równaniami różniczkowo-różnicowymi.
Ciągły- można opisać równaniami różniczkowymi.
Dyskretno-ciągły- można opisać równaniami różniczkowymi oraz różniczkowo-różnicowymi.
Stacjonarny- którego parametry można przedstawić w postaci stałych wielkości fizykalnych, niezmiennych w czasie.
Niestacjonarny- parametry należy przedstawić w postaci wielkości fizykalnych, zmiennych w czasie.
O parametrach skupionych- parametry są stałe bądź zmienne w czasie, lecz nie są funkcjami współrzędnych przestrzennych układu.
O parametrach rozłożonych- parametry są stałe bądź zmienne w czasie i są funkcjami współrzędnych przestrzennych układu.
Zdeterminowany- parametry fizykalne oraz wymuszenia są funkcjami stałymi lub zdeterminowanymi funkcjami czasu i zmiennej stanu układu
Stochastyczny- parametry fizykalne oraz wymuszenia są funkcjami losowymi o znanych, bądź zbadanych charakterystykach probabilistycznych.

Podstawowe elementy układów automatycznych:

- bezinercyjny - inercyjny I rzędu - z opóźnieniem czasowym - oscylacyjny - inercyjny II rzędu - całkujący - różniczkujący I rzędu

Impuls jednostkowy (Delta Diraca) d(t)=0 przy t nie=0 d(t)->niesk. przy t=0

Gdy warunek poniżej jest spełniony również spełniona jest f Diracka

f d(t)dt, czyli d(t)=lim (alfa->0) Ui(t) Ui - wartość skokowa, alfa - przedział czasu Przykład takiego wykresu może nawiązać do uderzeń a zatem d(t)=[d1(t)/dt] Pole powierzchni zawartej pod figurą impulsu jest w całym przedziale czasu równe 1. Delta Diracka jest pochodną po czasie funkcji Heaviside'a.

Nazwa	G(jw)	P(w)	G(w)	F(w)	A(w)
El. róż. idealny	kTjw	0	kTw	Pi/2	kTw
El. róż. rzecz.	P(w)+G(w)	[(kt^2*w^2)/ (1+T^2*w^2)]	[(kt*w)/ (1+T^2*w^2)]	Arctg1/TW	(Ktw*(pierw 1+T^2w^2))/ 1+T^2+w^2
El. opóźniający	K*e(-tojw)	K*costow	K*sintow	-tow	k
El. bezinercyjny	K	K	0	Arcth0=0	k
El inercyjny I rzedu	k/T(jw)+1	k/1+t^2w^2	-ktw /1+t^2w^2	arctgTW	k/ pierw(1+t^2w^2)
El całk. idealny	k/jw lub 1/jtw	0	-k/w lub -1/tw	Arctg(-niesk)- pi/2	K/w lub 1/tw
El. całk. Rzeczywisty	-j*k/ w(t^2w^2+1)	-kT/ (t^2w^2+1)	-k/ w(t^2w^2+1)	Arcth1/tw	k/ w*pierw(t^2w^2+1)

Zbiornik z swobodnym wypływem

A1(t) [m^3/s]-natęzenie przepływu cieczy na wlocie do zbiornika

A2(t) - natężenie przepływu cieczy na wylocie zbiornika

h(t) [m] - wysokość poziomu cieczy w zbiorniku

s(t) [m^2] - [powierzchnia tafli

Układ matematyczny:

V(t) objętość cieczy w zbiorniku przy czym deltaV(t)=Sdeltah(t), a przy tym deltat->dt,deltaV(t) oraz deltah(t)->dh(t)

można zapisać dV(t)=Sdh(t) natomiast Q2(t)=a*pierw(h(t)) lub Q2(t)=h(t)/Rh(h) gdzie Rh(h)=h/pierw(h)*a=[pierw(h)*h/h*a]- [pierw(h)/a][s/m^2]

Bilans zbiornika:

Q1(t)=Q2(t)+[dV(t)/dt] gdzie dV(t)/dt - natężenie przyrostu objętości cieczy w zbiorniku.

Jeśli dV(t)/dt będzie spadało to bilans będzie malał. To co wpływa musi się równać temu co wypływa:

Q1(t)=[h(t)/Rh(h)]+[S*dh(t)/dt] - Równanie różniczkowe przepływu cieczy przez zbiornik ze swobodnym wypływem.

Czwórnik RLC

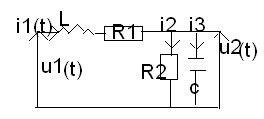
Z 2 prawa kirchoffa wynika U1(t)=L*di1(t)/dt+R1i1+U2(t), przy czym U2=R2i2(t) i3(t) = C*dU2(t)/dt

Z 1 prawa kirchoffa (i1 = i2+ i3)

U2(t)=R2i2(t) oraz i2(t)=C*dU2(t)/dt Uzyskuje się i1(t)=1/Rz*U2(t)+C*dU2(t)/dt

Równanie:

1/LC*U1(t)=[d^2U2(t)/dt^2]+[LR1R2C/R2LC]*[dU2(t)/dt]+[R1+R2/R2LC]*U2(t)

Równanie różniczkowe obwodu elektrycznego czwórnika rlc umożliwiające znalezienie odp ukł. U2(t) na sygnał wejściowy U1(t)

Transmitancja operatorowa o wielu wejściach i wyjściach

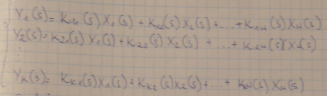
Regulatory o działaniu nieciągłym (przerywanym, przekaźnikowym, wielostawnym) zmieniają wartość wielkości sterującej obiektem w sposób przełączny, czyli wielkość ta może  przyjmować tylko 2 lub kilka wybranych wartości. Regulatory nieciągłe zbudowane są przeważnie z układów stykowych, stykowo - przekaźnikowych lub układów elektronicznych z przerzutnikami.

- regulator wielopołożeniowy (regulator dwu- i trójstawny)

Regulatory o działaniu ciągłym (przekaźnikowym) zmieniają wartość wielkości sterującej obiektem w sposób przełączny, czyli wielkość ta może  przyjmować tylko 2 lub kilka wybranych wartości. Regulatory nieciągłe zbudowane są przeważnie z układów stykowych, stykowo - przekaźnikowych lub układów elektronicznych z przerzutnikami.

- regulator proporcjonalny P
- regulator całkujący I
- regulator proporcjonalno-całkujący PI
- regulator proporcjonalno-różniczkujący PD
- regulator proporcjonalno-całkująco-różniczkujący PID

Regulatory o działaniu dyskretnym (cyfrowe) zmieniają wartość wielkości sterującej obiektem w podobny sposób jak regulatory nieciągłe - z tą różnicą, że zmiana wartości następuje tylko w wybranych chwilach czasu, a stopniowanie jest na tyle precyzyjne, że dla obiektu w praktyce niezauważalne. Działanie tych regulatorów opiera się na wykorzystaniu układów mikroprocesorowych lub komputerowych.

Układ jest dyskretny, jeżeli przynajmniej jeden jego sygnał ma charakter dyskretny, tzn. przyjmuje tylko określone wartości dla określonych argumentów. Zazwyczaj układy takie opisuje się równaniami różnicowymi.

---