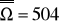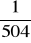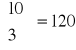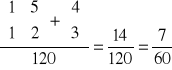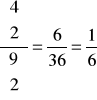Zadanie 6

Spośród cyfr: 1, 2, 3, 4, 5, 6, 7, 8, 9 losujemy kolejno po jednej cyfrze trzy razy, nie zwracając wylosowanej cyfry po każdym losowaniu.

1. Jakie jest prawdopodobieństwo zdarzenia, że otrzyma się liczbę 451, zapisując cyfry w kolejności losowania?

2. Oblicz prawdopodobieństwo zdarzenia, że wylosuje się trzy cyfry, którymi można zapisać liczbę 451.

3. Jakie jest prawdopodobieństwo zdarzenia, że uzyska się liczbę mniejszą od 451, zapisując cyfry w kolejności losowania?

Rozwiązanie: 

1. Określamy przestrzeń zdarzeń elementarnych: Będzie nią zbiór wariacji (ciągów - "losujemy kolejno ..") bez powtórzeń ("nie zwracając...").

2. Liczba zdarzeń elementarnych to iloczyn liczb: 9, 8 i 7.(tyle jest możliwości wylosowania kolejnej liczby. Stąd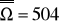 
   

3. Zdarzeniu z podpunktu (a)  odpowiada jedna możliwość (konkretne cyfry 4,5,1.  Stąd prawdopodobieństwo wynosi: P(A) =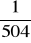
   

4. W przypadku drugiego zdarzenia wystarczy wypisać wszystkie liczby trzycyfrowe utworzone z użyciem każdej z cyfr 4,5,1. Tworzą one zbiór B

B = {145, 154, 415, 451, 514, 541} - czyli 6 „zdarzeń elementarnych”.

Otrzymujemy prawdopodobieństwo: P(B) =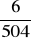

5. W podpunkcie c) zadania należy dokonać pewnej klasyfikacji:

• Najpierw obliczamy liczbę zdarzeń, w których za pierwszym razem uzyskamy cyfrę ze zbioru: {1, 2, 3}.

Mamy wtedy: 3⋅8⋅9 możliwości (gdyż za drugim (trzecim losowaniem) wybieramy jakąkolwiek liczbę z pozostałych)

Otrzymujemy liczbę możliwości: 216

-   Następnie  obliczamy liczbę zdarzeń, w których za pierwszym razem wylosowano cyfrę 4, za drugim razem cyfrę mniejszą od 5.

Mamy wtedy: 3⋅7 możliwości (gdyż drugą z wylosowanych cyfr może być 1,2 lub 3, a trzecia dowolną z pozostałych)

Otrzymujemy liczbę możliwości: 21

Dodajemy otrzymane liczby, co daje liczbę 237, czyli prawdopodobieństwo wynosi

P(C )=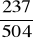

Zadanie 7

Na loterii jest 10 losów, wśród których jeden los wygrywa całą stawkę, 4 losy wygrywają po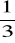
stawki, a pozostałe losy są puste. Jakie jest prawdopodobieństwo, że kupując trzy losy wygrywamy:

(a)    dokładnie całą stawkę?

(b)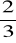    
stawki, pod warunkiem, że pierwszy kupiony los był pusty

Rozwiązanie

1. W naszym zadaniu mamy jakby „kule” trzech kolorów: jeden to 1 wygrywający los, drugi to 4 losy po jednej trzeciej stawki i trzeci to 5 losów pustych.

2. Wygraniu dokładnie całej stawki sprzyjają następujące możliwości (Obliczamy prawdopodobieństwo sumy zdarzeń rozłącznych!): 1 los wygrywający i dwa puste, trzy losy po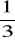 
   stawki!

3. Zdarzeniem elementarnym jest każdy podzbiór utworzony z elementów zbioru 10 elementowego.  Liczba zdarzeń elementarnych to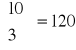
   .

4. Prawdopodobieństwo dla podpunktu (a) obliczamy następująco:

P(A) =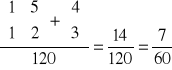

5. Prawdopodobieństwo dla podpunktu (b) dotyczy sytuacji, w której musimy uwzględnić dodatkowy warunek (czasami określany jako „nowa” przestrzeń omega!) „Pierwszy wylosowany los był pusty”.

Wygramy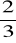 
stawki, tylko wtedy, gdy następne losy będą z „drugiego” koloru. Wtedy prawdopodobieństwo obliczamy podobnie, ale .... dla 9 kul!

6. Mamy:  P(B) =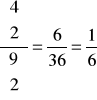
   .   Mamy tutaj do czynienia z 9 kulami, wśród których są  4 kule puste.

Ćwiczenie 1

Rozwiąż zadania 1- 12 str. 105-107 z podręcznika.

---