Luiza Pańczyk

definicja:

Macierzą m × n (tzn. o m wierszach i n kolumnach) o wyrazach w zbiorze X nazywamy tablicę:

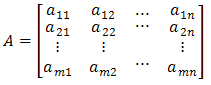
gdzie a_i,j należy do X dla 1 ≤ i ≤ m, 1 ≤ j ≤ n.

Rzędy poziome macierzy A nazywamy wierszami, rzędy pionowe kolumnami.

Zbiór wszystkich macierzy m × n o wyrazach ze zbioru X oznaczamy M_m×n(X).

Na przykład M_m×n(R) oznacza zbiór wszystkich macierzy rzeczywistych o wymiarach m × n.

definicja:

Układowi równań:

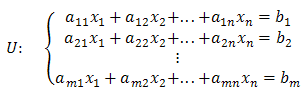
możemy przypisać macierz:

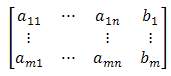
Taką macierz nazywamy macierzą rozszerzoną układu U.

Macierz:

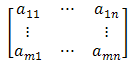
nazywamy macierzą współczynników układu U.

Na macierzach (podobnie jak na układach równań) można wykonywać trzy proste operacje:

- dodać do jednego wiersza macierzy inny wiersz pomnożony przez liczbę,

- zamienić dwa wiersze miejscami,

- pomnożyć wiersz przez liczbę różną od zera.

Te trzy opisane powyżej operacje nazywamy operacjami elementarnymi na wierszach.

Operacje elementarne na wierszach macierzy odpowiadają takim samym operacjom na równaniach układu równań.

Ciągłe przepisywanie całego układu równań jest dość czasochłonne. Dlatego warto wykonywać działania jedynie na macierzy odpowiadającej danemu układowi, aby na końcu tylko odczytać z niej rozwiązanie.

Przy takim podejściu całe zadanie sprowadza się do przekształcenia macierzy na postać schodkową zredukowaną. Z takiej postaci od razu widać rozwiązania układu równań.

definicja:

Mówimy, że macierz A należąca do Mm×n(R) jest w postaci schodkowej, jeżeli A spełnia warunki:

- każdy wiersz zerowy (składający się z samych zer) znajduje się poniżej każdego wiersza niezerowego,

- w każdym wierszu pierwszy (licząc od lewej) niezerowy wyraz znajduje się w kolumnie stojącej na prawo od pierwszego niezerowego wyrazu wiersza poprzedniego.

Mówiąc intuicyjnie - macierz jest w postaci schodkowej, jeżeli w kolejnych wierszach występuje na początku coraz więcej zer (kolejne wiersze macierzy przypominają schodki).

definicja:

Mówimy, że macierz jest w zredukowanej postaci schodkowej, jeżeli spełnia warunki:

- jest w postaci schodkowej,

- w każdym wierszu pierwszy niezerowy wyraz jest równy 1, a ponadto inne wyrazy w jego kolumnie są zerami.

Uwaga:

Każdą macierz można za pomocą operacji elementarnych sprowadzić do postaci schodkowej zredukowanej!

Powyższa uwaga jest niezwykle ważna, ponieważ dzięki niej możemy rozwiązywać dowolnie skomplikowane układy równań liniowych. Wystarczy sprowadzić do postaci schodkowej zredukowanej macierz odpowiadającą takiemu układowi, a następnie odczytać z niej rozwiązanie.

definicja:

Macierz transponowana do macierzy A to macierz A^T, która powstaje przez zamianę jej wierszy na kolumny i kolumn na wiersze.

definicja:

Wektory nazywamy wektorami liniowo zależnymi, jeżeli istnieją takie stałe (z których co najmniej jedna jest różna od zera), że:

.

Na odwrót powiedzielibyśmy, że dwa wektory są liniowo niezależne, jeżeli NIE istnieją takie stałe (z których co najmniej jedna jest różna od zera), że:

.

definicja:

Rzędem wierszowym macierzy nazywamy maksymalną liczbę liniowo niezależnych wierszy tej macierzy.

Rzędem kolumnowym macierzy nazywamy maksymalną liczbę liniowo niezależnych kolumn tej macierzy.

Rząd wierszowy jest równy rzędowi kolumnowemu danej macierzy. Wspólną wartość rzędu wierszowego i kolumnowego nazywamy rzędem macierzy.

Inaczej mowiąc, rząd macierzy to stopień największego, niezerowego minora tej macierzy lub rząd macierzy równy jest ilości liniowo niezależnych wierszy lub kolumn w macierzy. Rząd macierzy zapisujemy symbolicznie rzA.

Rząd macierzy A jest równy r wtedy i tylko wtedy, gdy

- istnieje niezerowy minor stopnia r macierzy A.

- każdy minor macierzy A stopnia wyższego niż r (o ile taki istnieje) jest równy zeru.

Praktyczną metodą obliczania rzędu macierzy jest metoda Gaussa, gdzie należy za pomocą operacji elementarnych sprowadzić macierz do macierzy schodkowej. Wówczas wszystkie niezerowe wiersze są liniowo niezależne i można łatwo odczytać rząd macierzy. Stopień macierzy jest wtedy liczbą znaczących równań tego układu, czyli liczbą schodków.

Twierdzenie Kroneckera-Capellego

Twierdzenie Kroneckera-Capellego wykorzystujące rząd macierzy jest naprawdę bardzo proste. Mając dowolny (niewiadomych nie musi być tyle samo, co równań) układ równań:

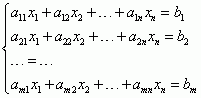
Nasz układ ma m równań i n niewiadomych. Rząd macierzy głównej to rząd macierzy utworzonej ze współczynników przy niewiadomych, czyli:

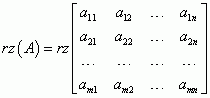
Nie musi to być macierz kwadratowa. Rząd macierzy uzupełnionej to rząd macierzy utworzonej ze współczynników przy niewiadomych z dodaną kolumną wyrazów wolnych (po prawych stronach równości):

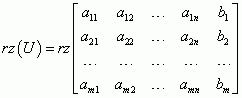
Twierdzenie Kroneckera-Capellego stwierdza, że układ ma rozwiązania wtedy i tylko wtedy, gdy rząd macierzy głównej równy jest rzędowi macierzy uzupełnionej:

rz(A)=rz(U)

Z twierdzenia wynikają następujące wnioski:

1. Jeżeli rząd macierzy głównej, rząd macierzy uzupełnionej i liczba niewiadomych w układzie są równe to układ równań ma dokładnie jedno rozwiązanie.

2. Jeżeli rząd macierzy głównej jest taki sam jak rząd macierzy uzupełnionej, ale jest mniejszy od liczby niewiadomych to układ równań ma nieskończenie wiele rozwiązań.

3. Jeżeli rząd macierzy głównej jest różny od rzędu macierzy uzupełnionej , wtedy układ równań nie ma rozwiązań.

Źródła:

http://www.matemaks.pl/macierze.php

http://blog.etrapez.pl/macierze/rzad-macierzy/

http://www.math.edu.pl/rzad-macierzy

http://blog.etrapez.pl/macierze/rzad-macierzy-w-twierdzeniu-kroneckera-capellego/