|
Imię i nazwisko: Adam Sobantka |
Ćw. 15 Wyznaczenie ładunku właściwego elektronu e/m metodą magnetronową |
||
|
Kierunek i rok: Fizyka I uzupełniająca |
Ocena z kolokwium:
…………………..
…………………... Data/podpis |
Ocena ze sprawozdania:
…………………...
…………………... Data/podpis |
Ocena końcowa:
…………………...
…………………... Data/podpis |
|
Nazwisko prowadzącego zajęcia:
|
|||
Teoria
Ruch ładunku w polu elektrycznym i magnetycznym
Na ładunek q w polu elektrycznym o natężeniu E działa siła:
![]()
(1)
której wartość nie zależy od prędkości poruszającego się ładunku. Natomiast pole magnetyczne oddziałuje na ładunki elektryczne siłą zwaną siłą Lorentza:
![]()
(2)
gdzie vjest prędkością ładunku, a B- indukcją pola magnetycznego. Z własności iloczynu wektorowego wynika, że wektor siły jest prostopadły do płaszczyzny wyznaczonej przez wektory
v i5, a jego zwrot wyznacza reguła śruby prawo skrętnej. Wartość siły Lorentza wynosi:
![]()
(3)
Jak łatwo zauważyć, pole magnetyczne nie działa na ładunek elektryczny wówczas, gdy ładunek nie porusza się (v = 0) lub gdy porusza się w kierunku linii indukcji pola magnetycznego
(wtedy sinus kąta między wektorami v i B równa się zero). Siła działająca na ładunek będzie miała wartość największą, gdy ruch ładunku będzie się odbywał prostopadle do linii indukcji
magnetycznej B . Ponieważ siła Lorentza jest zawsze skierowana prostopadle do kierunku ruchu ładunku, to (dla stałego pola magnetycznego) praca wykonana przez tę siłę nad ładunkiem
wynosi zero. Dla elementu toru ładunku o długości dL praca ta, dW, wynosi F-dL - jest ona
równa zero, ponieważ wektory F i dL są zawsze prostopadle. Z tego powodu stałe pole magnetyczne nie może zmienić energii kinetycznej poruszającego się ładunku, a zatem i wartości prędkości; może tylko zmienić kierunek jego ruchu.
Całkowita siła działająca na ładunek znajdujący się jednocześnie w polach elektrycznym i magnetycznym jest sumą wektorową sił określonych wzorami (1) i (2) i wyraża się wzorem:
![]()
(4)
Rozpatrzmy przypadek, gdy elektron wlatuje z prędkością v do obszaru, w którym działa
tylko pole magnetyczne o kierunku linii indukcji B równoległym do osi OZ i prostopadłym do wektora prędkości (rys. 1).
Z
definicji siły Lorentza (2) i (3) wynika, że siła działająca na
cząstkę leży na płaszczyźnie XY i jej wartość wynosi![]() Ponieważ
przyśpieszenie styczne do toru cząstki
Ponieważ
przyśpieszenie styczne do toru cząstki
jest równe zeru, to wektor prędkości ma stałą wartość. Ruch może odbywać się tylko w płaszczyźnie XY i siła będzie zawsze prostopadła do kierunku ruchu. Również przyśpieszenie
cząstki a = F/m ma stałą wartość i jest skierowane prostopadle do prędkości.
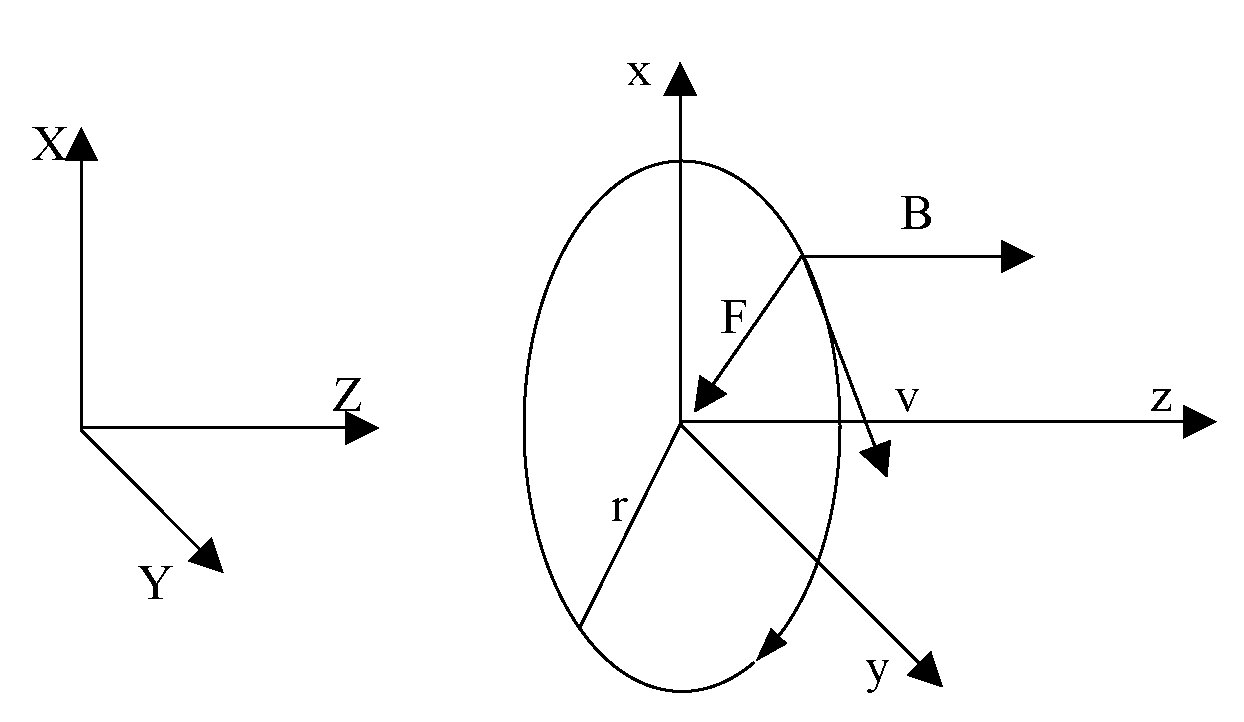
Rys. 1 Ruch ładunku w polu magnetycznym.
Ruchem o takich własnościach jest ruch jednostajny po okręgu, w którym siła Lorentza jest zarazem siłą dośrodkową:

(5)
gdzie r - jest promieniem okręgu, po którym porusza się cząstka. Łatwo z ostatniego wzoru obliczyć ten promień:
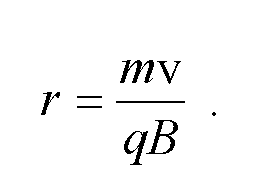
(6)
Można też obliczyć czas zataczania jednego okręgu przez poruszający się ładunek, czyli tak zwany okres obiegu:
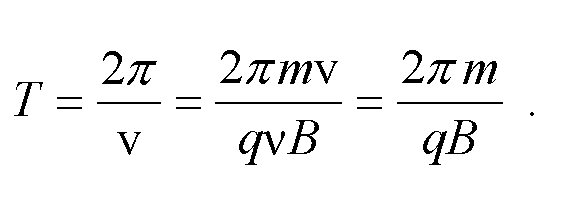
(7)
Czas ten nie zależy od prędkości ładunku, a tylko od wartości pola magnetycznego i stosunku masy cząstki do jej ładunku. Powyższe cechy ruchu ładunków w polu magnetycznym i elektrycznym zostały wykorzystane przy budowie wielu przyrządów pomiarowych, takich jak np. spektrometry masowe, komory pęcherzykowe, cyklotrony, itp.
Przeanalizujmy
teraz sytuację, gdy elektron porusza się w obszarze, w którym
działają oba
pola:
magnetyczne i elektryczne, tak
jak pokazano to na rys. 2. Kierunki wektorów natężeń pól
elektrycznego i magnetycznego są do siebie równoległe, natomiast
kierunek prędkości elektronu tworzy z kierunkami wektorów natężeń
pól kąt a.
Wektor
prędkości v rozkładamy na dwie składowe:
prostopadłą![]() i
równoległą
i
równoległą![]() do
wektora indukcji magnetycznej.
do
wektora indukcji magnetycznej.
Ruch w każdym z kierunków rozpatrujemy osobno. W kierunku prostopadłym do kierunku linii sił pól elektrycznego i magnetycznego na elektron działa, zgodnie ze wzorem (3), siła Lorentza równa:
![]()
(8)
Zgodnie z wcześniejszymi rozważaniami ruch w tej płaszczyźnie (prostopadłej do kierunku linii sił pól elektrycznego i magnetycznego) będzie ruchem po okręgu o promieniu wyliczonym ze wzoru:
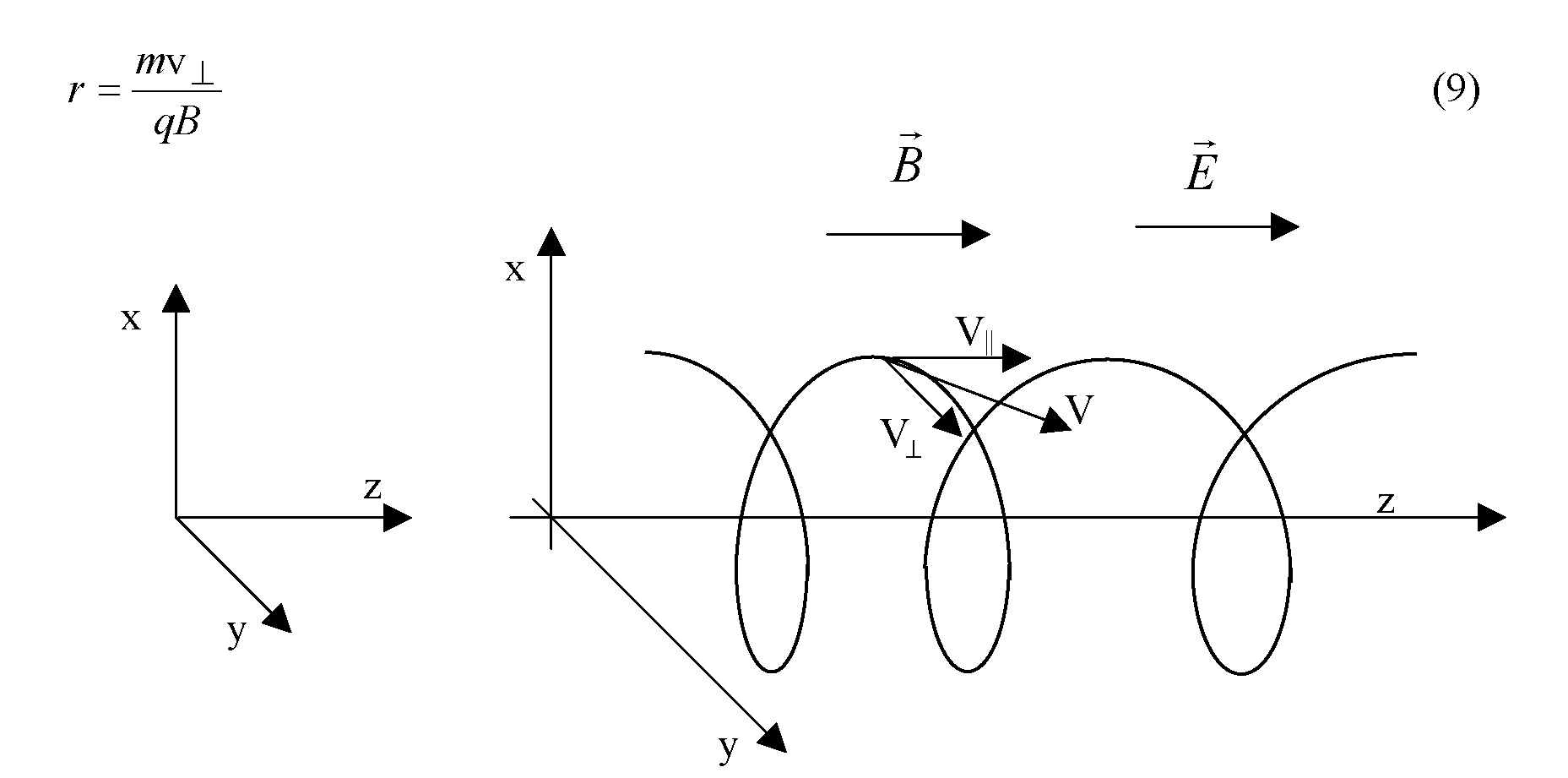
Rys. 2 Ruch elektronu w polach elektrycznym i magnetycznym.
Natomiast
w kierunku równoległym (wzdłuż linii sił obu pól) na cząstkę
poruszającą się w tym kierunku z prędkością![]() działa
tylko siła od pola elektrycznego. W przypadku jego nieobecności
elektron poruszałby się w tym kierunku ze stałą
prędkością
działa
tylko siła od pola elektrycznego. W przypadku jego nieobecności
elektron poruszałby się w tym kierunku ze stałą
prędkością![]() (składowa
(składowa
siły Lorentza wzdłuż tego kierunku jest równa zeru), a złożenie ruchów w obu kierunkach dawałoby w efekcie ruch elektronu po linii śrubowej o stałym skoku. Obecność pola elektrycznego powoduje, że elektron w tym kierunku porusza się ruchem jednostajnie przyśpieszonym, co po złożeniu daje ruch po linii śrubowej o zmiennym, zwiększającym się skoku.
Wyznaczanie wartości e/m metoda magnetronu.
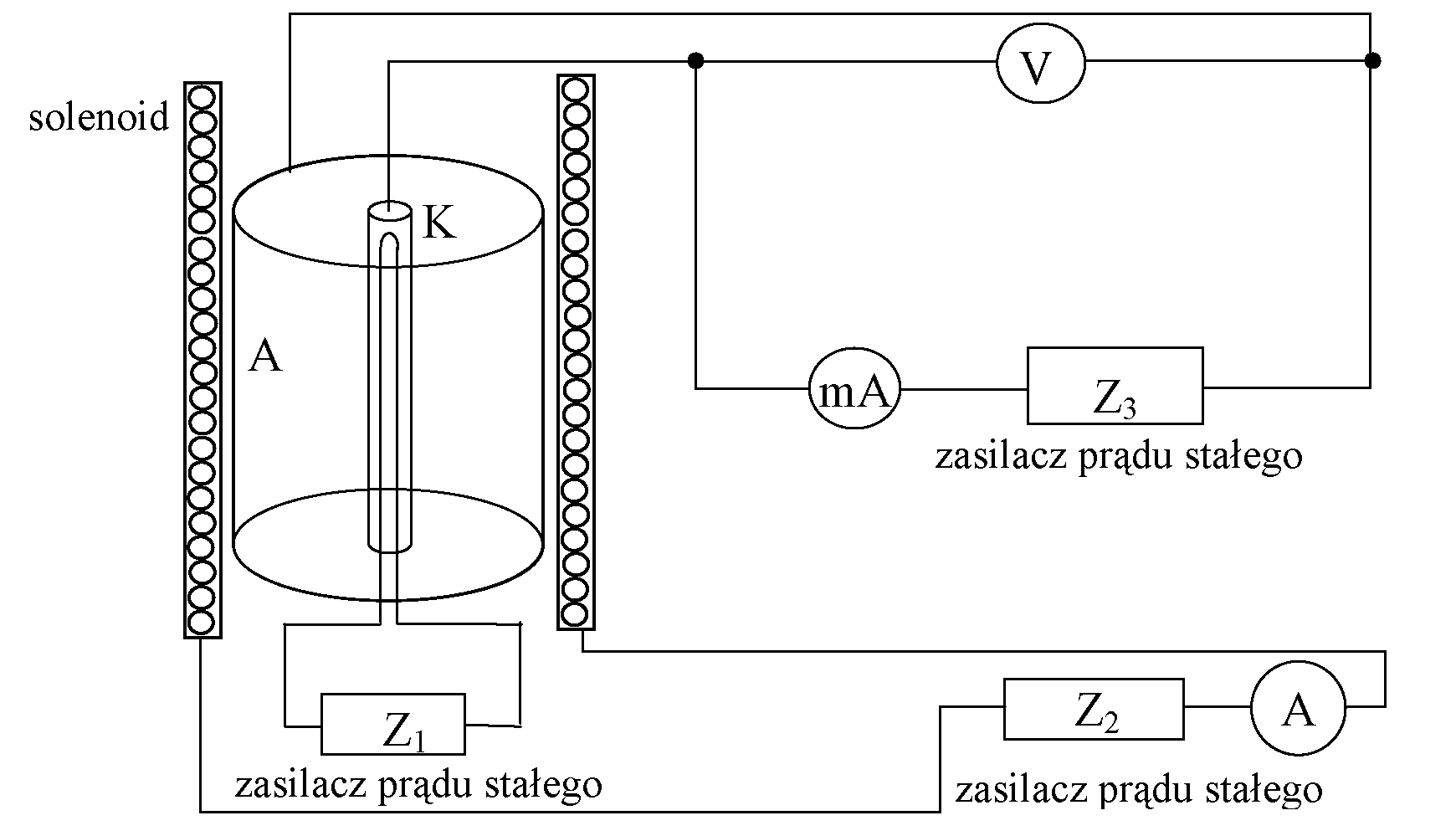
Rys. 3 Schemat budowy magnetronu i układu do pomiaru wartości e/m. A - anoda, K - katoda, Zj - zasilacz obwodu żarzenia katody, Z2 - zasilacz prądu uzwojenia cewki, Z3 - zasilacz napięcia anodowego.
Z żarzonej katody emitowane są elektrony (zjawisko termoemisji). Poruszają się one od katody do anody wskutek obecności pola elektrycznego. Przyłożenie zewnętrznego pola
magnetycznego powoduje zakrzywienie toru ich ruchu, a dla pewnej, krytycznej wartości pola magnetycznego, zakrzywienie jest tak duże, że elektrony przestają docierać do anody. Efekty działania pola magnetycznego na ruch elektronów w magnetronie przedstawia rys.4.
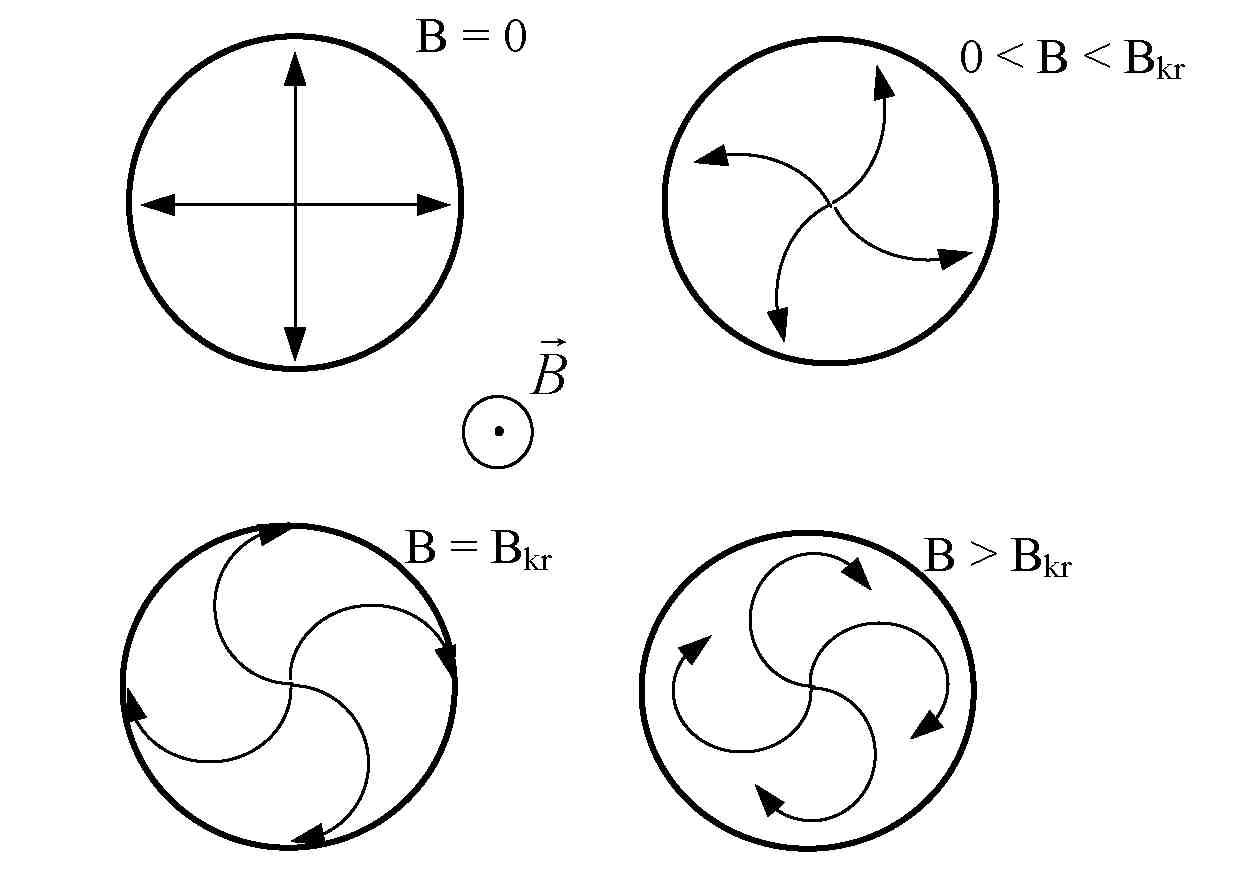
Rys. 4 Wpływ pola magnetycznego na ruch elektronów od katody do anody.
Rozpatrując
zależność prądu anodowego od zewnętrznego pola magnetycznego,
możemy w prosty sposób wyznaczyć wartość stosunku ładunku do
masy elektronu -![]() W
tym celu
W
tym celu
przeanalizujemy ruch elektronu w magnetronie od katody do anody w obecności pola magnetycznego, tak jak na rys.5, gdzie między anodę i katodę jest przyłożone napięcie U a lampa
znajduje
się w polu magnetycznym o indukcji![]()
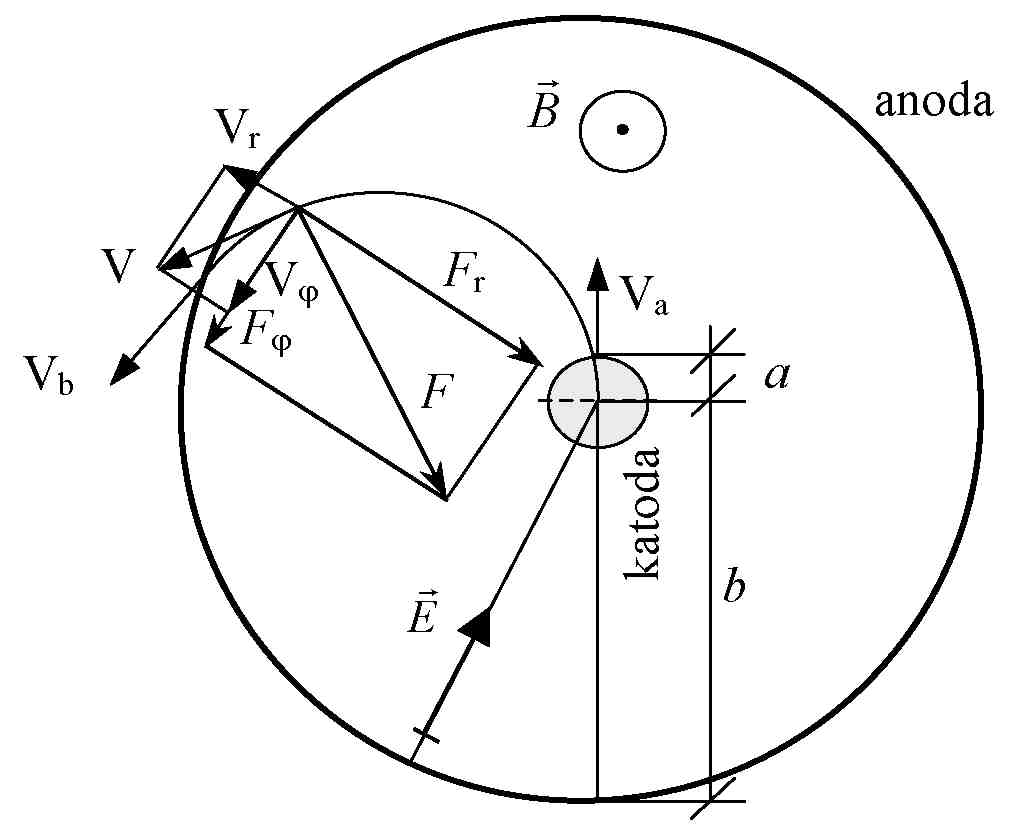
Rys. 5 Siły działające w magnetronie na poruszający się elektron.
Siłę
Lorentza, podobnie jak prędkość, możemy rozłożyć na dwie
składowe: w kierunku do ośrodka lampy (wzdłuż promienia)
![]() i
w kierunku prostopadłym do promienia
i
w kierunku prostopadłym do promienia
![]() .
Całkowita
.
Całkowita
siła
działająca na elektron będzie miała składowe![]() oraz
oraz![]() (siła
(siła![]() pochodzi
od różnicy
pochodzi
od różnicy
potencjałów
pomiędzy anodą i katodą). Siły![]() działają
wzdłuż promienia r i nie mogą
działają
wzdłuż promienia r i nie mogą
zmienić
momentu pędu elektronu względem osi lampy![]() ,
ponieważ
,
ponieważ
wektory![]() i
i
![]() są
równoległe). Moment pędu
są
równoległe). Moment pędu![]() elektronu
względem osi magnetronu (równy co do wartości bezwzględnej
elektronu
względem osi magnetronu (równy co do wartości bezwzględnej![]() może
zmienić jedynie składowa siły
może
zmienić jedynie składowa siły
Lorentza
![]() -
jej kierunek i wielkość określamy ze wzoru (2). Kierunek siły
-
jej kierunek i wielkość określamy ze wzoru (2). Kierunek siły
![]() będzie
będzie
prostopadły
do wektora indukcji magnetycznej![]() i
składowej prędkości
i
składowej prędkości![]() .
Na podstawie (2) możemy napisać:
.
Na podstawie (2) możemy napisać:
![]()
(10)
Należy
podkreślić, że wartość siły Lorentza zmienia się, gdyż
zmienia się wartość składowej prędkości![]() wskutek
obecności pola elektrycznego. Stosując do tej zależności drugą
zasadę dynamiki Newtona dla ruchu obrotowego:
wskutek
obecności pola elektrycznego. Stosując do tej zależności drugą
zasadę dynamiki Newtona dla ruchu obrotowego:
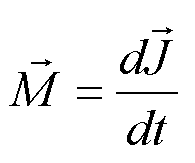
(11a)
gdzie![]() jest
momentem siły, którego wartość zgodnie ze wzorem (10) wynosi:
jest
momentem siły, którego wartość zgodnie ze wzorem (10) wynosi:
![]()
(11b)
a J - jest momentem pędu o wartości:
![]()
(11c)
Podstawiając
wyrażenia (1 Ib) i (lic) do wzoru (1 la) po uwzględnieniu, że we
wzorze (11 b)
![]() otrzymuj
emy:
otrzymuj
emy:
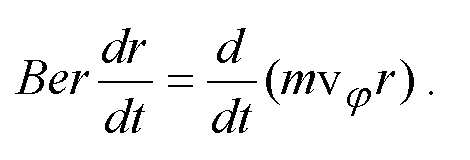
(12)
Mnożąc ostatnie równanie przez dt\ całkując stronami wzdłuż promienia od katody do anody, czyli od wartości a do b :

(13)
otrzymujemy :
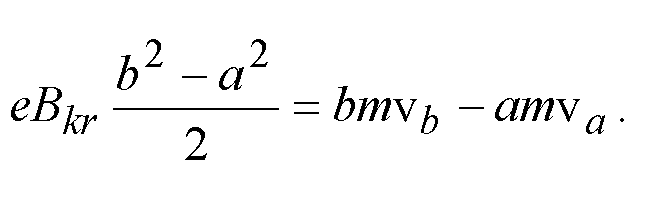
(14)
Bez
popełnienia znaczącego błędu możemy przyjąć, że![]() równa
się zero, ponieważ większość elektronów opuszcza
katodę dokładnie w kierunku od anody do katody i
nie posiada składowej wielkości
równa
się zero, ponieważ większość elektronów opuszcza
katodę dokładnie w kierunku od anody do katody i
nie posiada składowej wielkości![]() Natomiast
Natomiast![]() można
obliczyć w bardzo prosty sposób. Można przyjąć, że
elektrony docierając do anody posiadają tylko składową
prędkości
można
obliczyć w bardzo prosty sposób. Można przyjąć, że
elektrony docierając do anody posiadają tylko składową
prędkości![]() (dla
(dla![]() kierunek
prędkości elektronów jest styczny do powierzchni anody - porównaj
rys.5).
kierunek
prędkości elektronów jest styczny do powierzchni anody - porównaj
rys.5).
Energia kinetyczna elektronów równa się pracy sił pola elektrycznego:
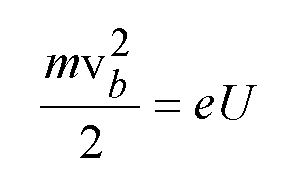
Stąd:
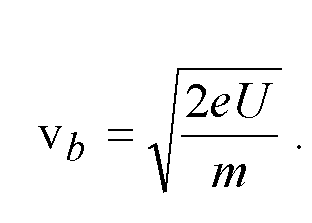
Podstawiamy otrzymany wynik do równania (14) :
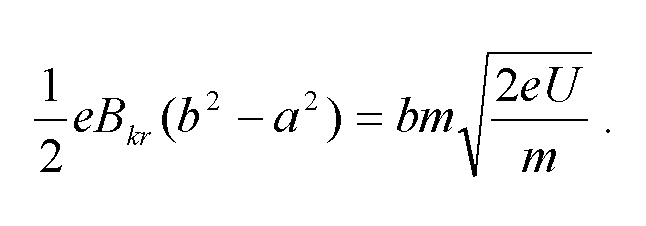
(15) (16)
(17)
Wartość
indukcji
![]() można
powiązać z natężeniem przepływającego
można
powiązać z natężeniem przepływającego
![]() przez
cewkę
przez
cewkę
wytwarzającą pole, stosując wzór na wartość indukcji pola magnetycznego w solenoidzie:
gdzie
\x
- przenikalność
magnetyczna ośrodka,![]()
![]()
(18)
N-
liczba zwojów cewki na jednostkę jej długości. Po prostych
przekształceniach wzoru (17), przy uwzględnieniu (18),
otrzymamy wzór na interesującą nas wartość
przyjmujemy![]() (dla
próżni
(dla
próżni![]() ):
):
-
stała magnetyczna próżni,

(19)
W celu wyznaczania stosunku e/m konieczne jest określenie wartości prądu krytycznego, przy którym przestaje płynąć prąd anodowy. Gdyby wszystkie elektrony miały jednakową prędkość początkową (a tym samym i końcową), to zależność prądu anodowego od indukcji pola magnetycznego wyglądałaby tak, jak na rys.óa i wartość prądu krytycznego byłaby wartością, dla której prąd anodowy maleje do zera.
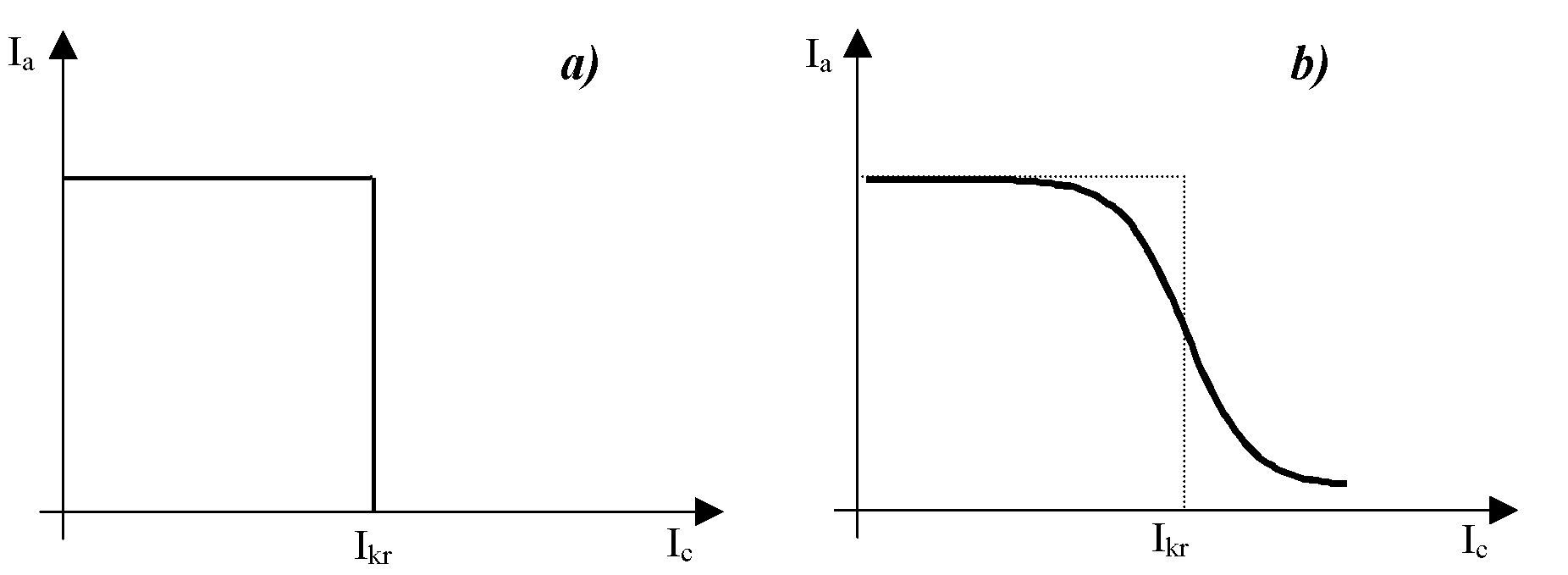
Rys. 6 Zależność prądu anodowego od prądu płynącego przez cewkę w przypadku: a) idealnym, b) rzeczywistym.
Tak jednak nie jest, gdyż elektrony opuszczają katodę z różnymi prędkościami (rozkład prędkości elektronów opuszczających katodę jest rozkładem Maxwella - Boltzmanna),
a dodatkowo zderzają się ze sobą na drodze od katody do anody. W efekcie wartość pola krytycznego dla różnych elektronów jest różna, a wykres prądu anodowego w funkcji prądu płynącego przez cewkę ma charakter jak na rys.ób. Za wartość prądu krytycznego przyjmujemy tę wartość, dla której krzywa ma punkt przegięcia.
Wyznaczanie wartości e/m metodą ogniskowania wiązki elektronowej (pole magnetyczne równolegle do osi lampy oscyloskopowej).
Rys.7
przedstawia poglądowo schemat lampy oscyloskopowej i wybrany układ
współrzędnych, w którym będzie opisywany ruch elektronów.
Elektrony emitowane przez katodę są przyśpieszane w stałym polu
elektrycznym (napięcie między anodą i katodą wynosi U) do
prędkości![]() określonej
wzorem (16) - wektor
określonej
wzorem (16) - wektor![]() jest
skierowany wzdłuż osi Z. Rozpędzone do prędkości
jest
skierowany wzdłuż osi Z. Rozpędzone do prędkości
![]() elektrony
poruszają się w jednorodnym polu magnetycznym o
indukcji
elektrony
poruszają się w jednorodnym polu magnetycznym o
indukcji
![]() skierowanym
wzdłuż osi Z wytworzonym przez zewnętrzną cewkę. Równocześnie
podczas przelotu elektronów przez płytki odchylające, znajdują
się one w słabym, zmiennym polu
skierowanym
wzdłuż osi Z wytworzonym przez zewnętrzną cewkę. Równocześnie
podczas przelotu elektronów przez płytki odchylające, znajdują
się one w słabym, zmiennym polu
elektrycznym
o natężeniu
![]() ,
którego wektor jest skierowany wzdłuż osi X. Pole to nadaje
,
którego wektor jest skierowany wzdłuż osi X. Pole to nadaje
elektronom
dodatkową, niewielką prędkość![]() prostopadłą
do pola magnetycznego
prostopadłą
do pola magnetycznego![]()
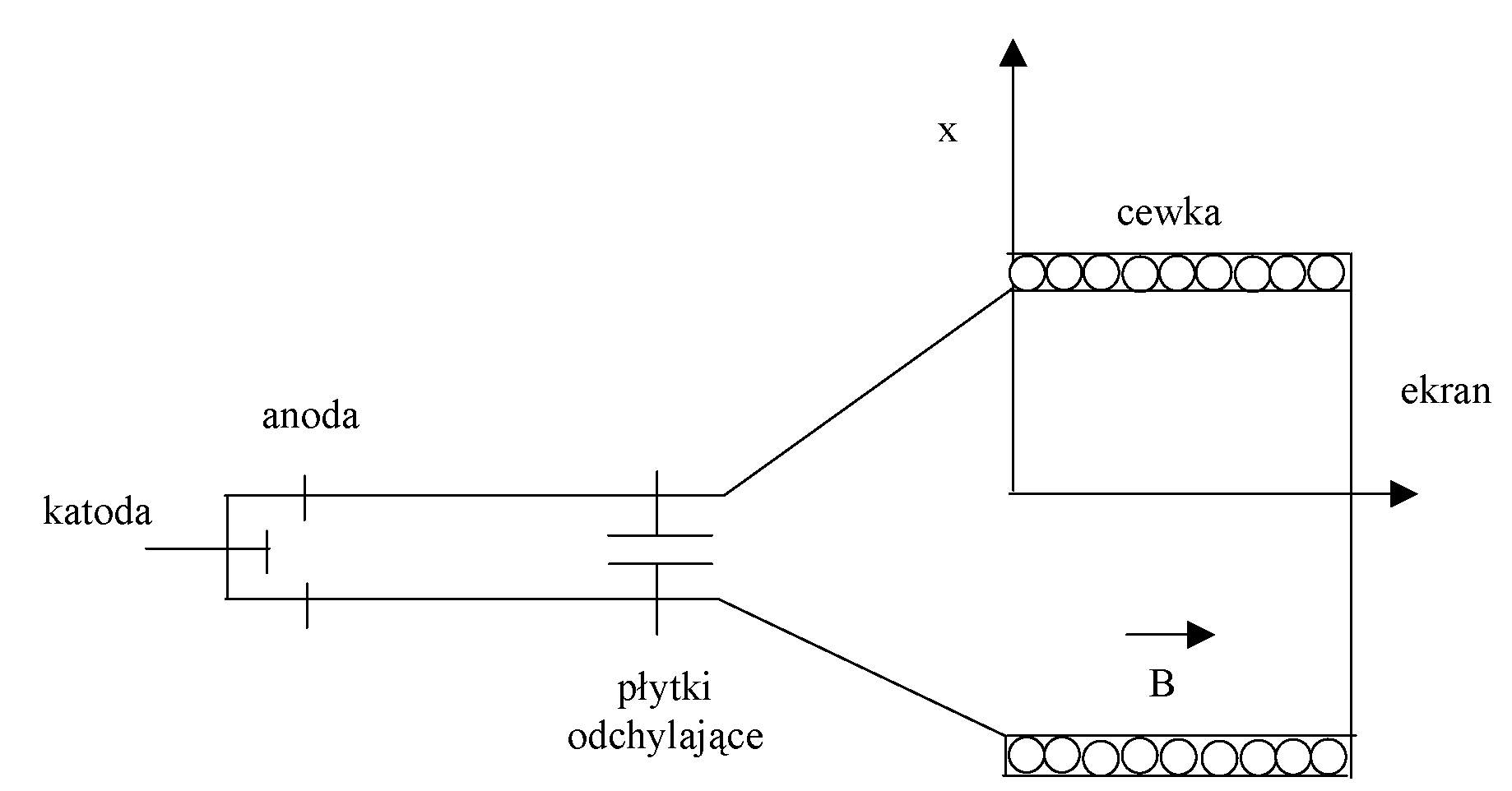
Rys. 7 Schemat lampy elektronowej z zaznaczonym układem współrzędnych.
Zgodnie z wcześniejszymi rozważaniami tory elektronów wlatujących do jednego pola magnetycznego pod kątem różnym od zerowego są liniami śrubowymi, leżącymi na powierzchni walca. Oś tego walca jest równoległa do kierunku pola magnetycznego, promień wynosi zgodnie z
(6)![]() (
(![]() -
jest składową prędkości elektronu w kierunku OY), a okres obiegu
(czas
-
jest składową prędkości elektronu w kierunku OY), a okres obiegu
(czas
zataczania
kąta![]() w
płaszczyźnie prostopadłej do osi walca) wynosi zgodnie ze wzorem
(7):
w
płaszczyźnie prostopadłej do osi walca) wynosi zgodnie ze wzorem
(7):
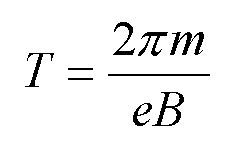 (20)
(20)
i nie zależy od prędkości elektronów. Obraz uzyskany na ekranie lampy oscyloskopowej odpowiada przecięciu torów elektronów płaszczyzną XY, prostopadłą do osi lampy.
Na
rys.8 przedstawiono obraz, który powstaje na ekranie, gdy do płytek
odchylających jest przyłożone napięcie zmienne![]() ,
w obecności stałego pola magnetycznego.
,
w obecności stałego pola magnetycznego.
W
takim przypadku elektrony uzyskują różne prędkości
![]() i
ich tory leżą na powierzchniach
i
ich tory leżą na powierzchniach
różnych walców.
Ze
względu na taki sam okres obiegu po okręgu (wzór (20)), obraz
obserwowany na ekranie odpowiada punktom uderzenia elektronów w
ekran po zatoczeniu tych samych kątów przez elektrony w ich ruchu
po różnych torach śrubowych. Kąt ten wynosi![]() ,
gdzie t oznacza
,
gdzie t oznacza
czas
przelotu elektronów od płytek odchylających do ekranu, a T czas
zataczania kąta![]() w płaszczyźnie prostopadłej do osi lampy.
w płaszczyźnie prostopadłej do osi lampy.
Gdy
kąt jest wielokrotnością![]() co
odpowiada przebyciu przez elektrony drogi
co
odpowiada przebyciu przez elektrony drogi![]()
elektrony spotykają się na osi lampy. Jeśli zmieniając napięcie U między katodą i anoda oraz indukcję magnetyczna B wewnątrz cewki, dobierzemy v i T tak, że na drodze od płytek odchylających do ekranu mieści się całkowita wielokrotność vT, to na ekranie lampy zamiast linii prostej zaobserwujemy świecący punkt. To zjawisko nazywamy zogniskowaniem wiązki.
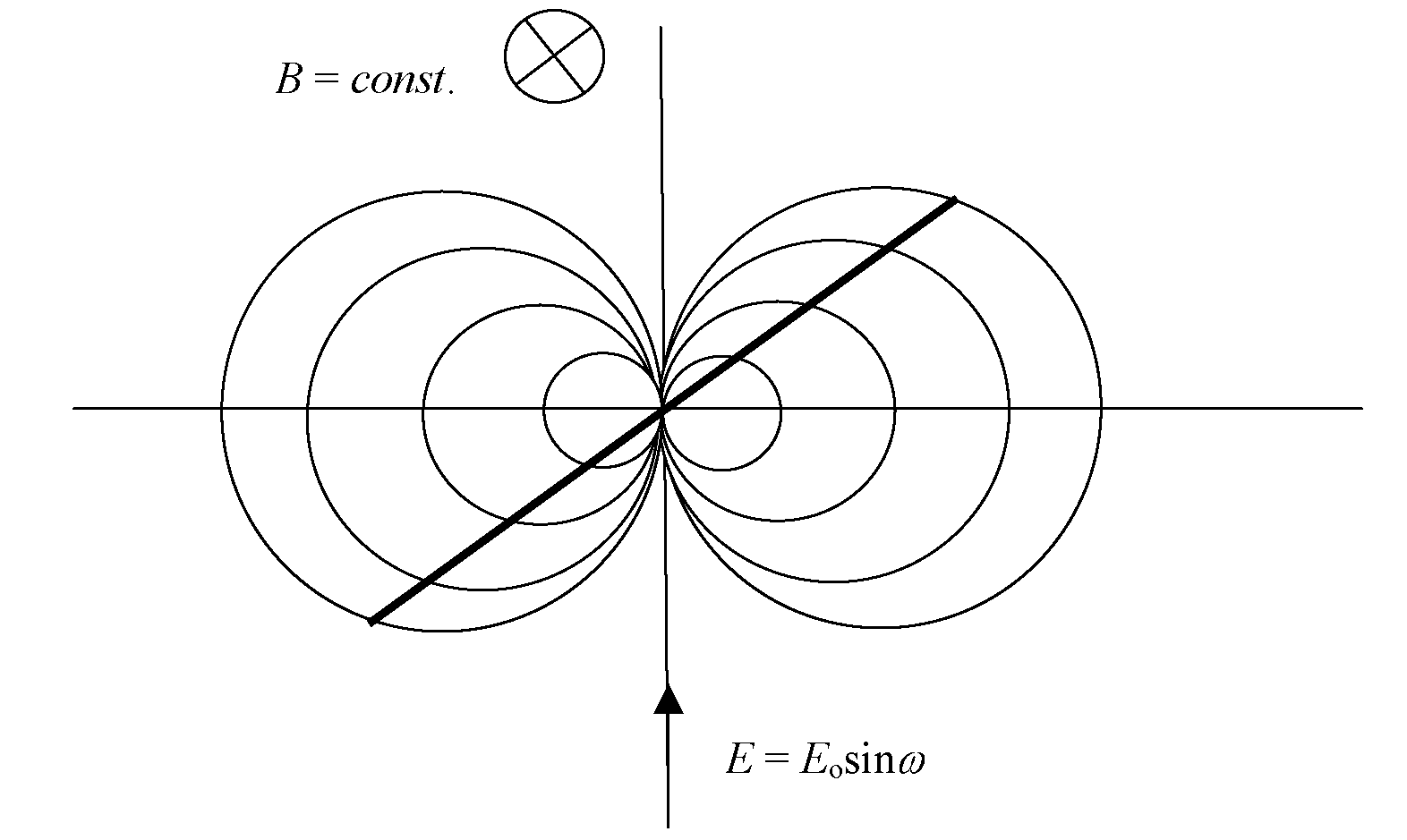
i
Rys. 8 Obraz powstający na ekranie oscyloskopu (grubsza linia) w przypadku, gdy do płytek odchylających jest przyłożone napięcie zmienne w obecności stałego pola magnetycznego. Cienkie linie oznaczają rzuty torów elektronów na płaszczyznę ekranu.
Dla warunku zogniskowania spełniony jest warunek nTv = d (n - krotność ogniskowania), skąd ze wzoru (20) wynika, ż
e![]() (21)
(21)
Ze wzoru (16) wyznaczamy prędkość otrzymujemy:
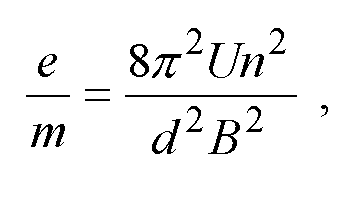
gdzie n = 1,2,3,..., natomiast d - jest długością obszaru działania pola magnetycznego.
Wyznaczanie wartości e/m metodą odchylania wiązki elektronowej (pole magnetyczne prostopadłe do osi lampy oscyloskopowej).
Rozpatrzmy teraz ruch elektronu w lampie oscyloskopowej tak, jak to przedstawiono na rysunku 9a. Wektor indukcji pola magnetycznego jest skierowany wzdłuż osi Z. Jest oczywiste, że w przypadku braku napięcia na płytkach odchylających i pola magnetycznego wewnątrz lampy, na ekranie lampy zaobserwujemy świecący punkt w jego środku. Przyłożenie stałego pola magnetycznego (wektor indukcji skierowany wzdłuż osi Y) spowoduje przesunięcie plamki o wartość x w kierunku pionowym.

Rys.9 Ruch elektronu w lampie elektronowej, gdy pole magnetyczne jest prostopadłe do kierunku ruchu elektronu: a) schemat układu, b) zależności geometryczne.
(23)
(24) (24)
Na
rys.9b przedstawiono zależności geometryczne prowadzące do
wyznaczania stosunku
![]() Łatwo
zauważyć, że z twierdzenia Pitagorasa mamy :
Łatwo
zauważyć, że z twierdzenia Pitagorasa mamy :

czyli po uproszczeniu:
![]()
Uwzględniając, że promień okręgu po którym poruszają się elektrony wynosi zgodnie z (6)
skąd:
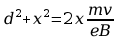 po pewnych przekształceniach
po pewnych przekształceniach
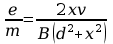
Wzór powyższy nie umożliwia bezpośredniego wyznaczenia wartości stosunku e/m, gdyż prędkość elektronu v jest zależna od tego stosunku. Sposób wyznaczenia wartości stosunku e/m podany jest w części poświęconej opracowaniu wyników. Wartość indukcji pola magnetycznego B obliczamy ze wzorów na indukcję w cewce (dokładne wzory na tabliczce przy ćwiczeniu), a wartość prędkości v ze wzoru (16).
Wyznaczanie wartości e/m przy użyciu cewek Helmholtza.
W tej części ćwiczenia wykorzystuje się specjalną lampę wypełnioną argonem pod małym ciśnieniem (około 0,1 Pa). Gaz ten odgrywa zasadniczą rolę w doświadczeniu, ponieważ elektrony zderzając się z cząsteczkami gazu powodują ich jonizację. Na skutek rekombinacji jonów argonu zachodzi zjawisko luminescencji i możliwa staje się obserwacja toru ruchu elektronów. Jednocześnie jony argonu oddziałując elektrostatycznie z elektronami, powodują ogniskowanie wiązki elektronowej. Elektrony są wyrzucane w obszar lampy za pomocą działa elektronowego, które przyspiesza je do energii E = eU. Lampa umieszczona jest między dwoma współosiowymi uzwojeniami z drutu miedzianego, zwanymi cewkami Helmholtza. Płynący przez cewki prąd elektryczny, powoduje powstanie wewnątrz lampy pola magnetycznego o wektorze indukcji magnetycznej B skierowanym prostopadle do osi lampy. Cewki Helmholtza mają duże rozmiary, by zapewnić otrzymanie jednorodnego pola magnetycznego wewnątrz lampy. Lampa może być obracana wokół własnej osi, co umożliwia zmianę kierunku prędkości elektronów względem kierunku pola magnetycznego. W pewnej pozycji ruch elektronów będzie odbywać się po okręgu, którego promień określa równanie (6). Wewnątrz lampy znajduje się również metalowa drabinka pokryta farbą fluoryzującą, pozwalającą na dokładny pomiar średnicy toru ruchu elektronów.
Jak
wynika z równania (6):![]() promień
toru elektronów możemy zmieniać,
promień
toru elektronów możemy zmieniać,
zmieniając wartość prędkości elektronów oraz wartość indukcji pola magnetycznego B. Wartość
prędkości
v możemy, zgodnie z równaniem
![]() zmieniać
zmieniając napięcie
zmieniać
zmieniając napięcie
przyspieszające U. Wyznaczając prędkość v z tego równania i podstawiając do równania (6), otrzymujemy po prostych przekształceniach:
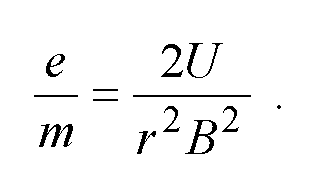 (25)
(25)
Wartość indukcji pola magnetycznego B możemy zmieniać, regulując natężenie prądu płynącego przez cewki Helmholtza. Przy założeniu, że przez obie cewki płynie identyczny prąd,
B
określone jest wzorem:![]() gdzie:
n - ilość zwojów = 154; R - promień cewek
gdzie:
n - ilość zwojów = 154; R - promień cewek
Helmholtza![]()
![]() -
przenikalność magnetyczna w próżni =
-
przenikalność magnetyczna w próżni =![]()
Podstawiając powyższe wartości do równania na indukcję pola otrzymujemy :
![]() [indukcja
będzie w T, jeśli prąd podstawi się w A] (26)
[indukcja
będzie w T, jeśli prąd podstawi się w A] (26)
W
ten sposób wartość![]() dla
wyżej opisanego układu pomiarowego w zależności od wielkości
fizycznych mierzonych w doświadczeniu wyniesie:
dla
wyżej opisanego układu pomiarowego w zależności od wielkości
fizycznych mierzonych w doświadczeniu wyniesie:
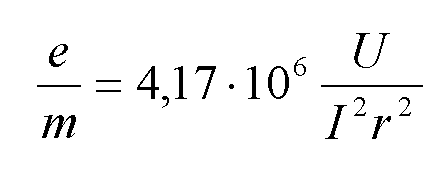 (29)
(29)
Aby
uzyskać![]() w
jednostkach podstawowych układu SI, należy podstawić wartość
napięcia V w woltach, prądu I w amperach, a promień okręgu r w
metrach.
w
jednostkach podstawowych układu SI, należy podstawić wartość
napięcia V w woltach, prądu I w amperach, a promień okręgu r w
metrach.
Dioda próżniowa - najprostszy rodzaj lampy elektronowej. Posiada dwie elektrody - anodę i katodę. Katoda jest źródłem elektronów. Próżniowe diody prostownicze wysokiego napięcia nazywa się kenotronami.
Diody pośrednio żarzone
E misja
z katody zachodzi pod wpływem wysokiej temperatury (emisja
termoelektronowa) - katoda jest żarzona najczęściej za pomocą
prądu elektrycznego. Cechą charakterystyczną diody jest
jednokierunkowy przepływ prądu elektrycznego: w kierunku od anody
do katody (elektrony poruszają się w kierunku odwrotnym). Prąd
płynie przez diodę tylko wtedy gdy anoda ma potencjał wyższy niż
katoda. Jednokierunkowe przewodzenie prądu zachodzi na skutek tego,
że tylko rozgrzana katoda ma zdolność emisji elektrony. Przy
polaryzacji w kierunku przewodzenia (anoda +, katoda) pole
elektryczne między elektrodami przyspiesza wyemitowane elektrony,
przy polaryzacji odwrotnej pole elektryczne hamuje ruch elektronów
nie dopuszczając do ich przepływu.
misja
z katody zachodzi pod wpływem wysokiej temperatury (emisja
termoelektronowa) - katoda jest żarzona najczęściej za pomocą
prądu elektrycznego. Cechą charakterystyczną diody jest
jednokierunkowy przepływ prądu elektrycznego: w kierunku od anody
do katody (elektrony poruszają się w kierunku odwrotnym). Prąd
płynie przez diodę tylko wtedy gdy anoda ma potencjał wyższy niż
katoda. Jednokierunkowe przewodzenie prądu zachodzi na skutek tego,
że tylko rozgrzana katoda ma zdolność emisji elektrony. Przy
polaryzacji w kierunku przewodzenia (anoda +, katoda) pole
elektryczne między elektrodami przyspiesza wyemitowane elektrony,
przy polaryzacji odwrotnej pole elektryczne hamuje ruch elektronów
nie dopuszczając do ich przepływu.
Pierwszą diodę próżniową skonstruował angielski fizyk John Ambrose Fleming w roku 1904, jednak do powszechnego użytku weszła dopiero pod koniec lat 20. Wcześniej była wykorzystywana rzadko - jako element prostowniczy dużej mocy.
Ze względu na zastosowanie diody dzielą się na detekcyjne, prostownicze i specjalne (np. mikrofalowe czy szumowe), co wymusza odpowiednie cechy konstrukcyjne. W europejskim systemie oznaczeń lamp diodom odpowiadają - po pierwszej literze definiującej rodzaj żarzenia - litery: A (dioda detekcyjna), B (podwójna dioda detekcyjna), Y (dioda prostownicza) oraz Z (podwójna dioda – duodioda – prostownicza). Przykładowe typy diod: EY88, AZ1, EAA91 (oznaczenia w systemie europejskim) lub RGN1054 (w systemie Telefunken).
Diody bespośrednio żarzone
N ajprostsze
diody prostownicze budowane były bez galwanicznego oddzielenia
włókna żarzenia od katody. Inaczej mówiąc włókno żarzenia
miało potencjał katody, co powodowało pewne utrudnienia w budowie
urządzeń z użyciem takich lamp (włókno żarzenia takiej diody
musiało być zasilane zazwyczaj z innego źródła, niż pozostałe
lampy i miało zazwyczaj wysoki potencjał dodatni względem
elektrycznej "masy" urządzenia), ale znacznie upraszczało
konstrukcję samej diody. Dioda taka nazywana była dodatkowym
określeniem "bezpośrednio żarzona". Taką właśnie
konstrukcję miały m.in. tak podwójna dioda AZ1, jak i
przedstawiona na fotografii poniżej podwójna dioda AZ12 - jedno
włókno żarzenia stanowiące wspólną katodę oraz dwie anody.
ajprostsze
diody prostownicze budowane były bez galwanicznego oddzielenia
włókna żarzenia od katody. Inaczej mówiąc włókno żarzenia
miało potencjał katody, co powodowało pewne utrudnienia w budowie
urządzeń z użyciem takich lamp (włókno żarzenia takiej diody
musiało być zasilane zazwyczaj z innego źródła, niż pozostałe
lampy i miało zazwyczaj wysoki potencjał dodatni względem
elektrycznej "masy" urządzenia), ale znacznie upraszczało
konstrukcję samej diody. Dioda taka nazywana była dodatkowym
określeniem "bezpośrednio żarzona". Taką właśnie
konstrukcję miały m.in. tak podwójna dioda AZ1, jak i
przedstawiona na fotografii poniżej podwójna dioda AZ12 - jedno
włókno żarzenia stanowiące wspólną katodę oraz dwie anody.
Emisja termoelektronowa - emisja elektronów przez rozgrzane ciała, w wyniku cieplnego pobudzenia elektronów. Dla większości ciał emisja termoelektronowa zachodzi w temperaturach powyżej 1000 kelwinów, a dla trudnotopliwych metali w temperaturach powyżej 2000K. Zjawisko znalazło szerokie zastosowanie w lampach elektronowych.
Zjawisko to było wzmiankowane w 1873 roku przez Guthrie, opisuje on że silnie rozgrzane żelazo umieszczone w próżni wysyła ładunki ujemne, ale nigdy nie udało mu się uzyskać ładunków dodatnich. Powtórnym odkrywcą był Thomas Edison (13 lutego 1880), który badał konstruowane przez siebie żarówki. On także zauważył jednokierunkowość prądu płynącego w bańce między rozgrzanym włóknem a zimną elektrodą.
Brytyjski fizyk John Ambrose Fleming zastosował opisane przez Edisona zjawisko do detekcji fal radiowych konstruując dwuelektrodową lampę próżniową (diodę), którą opatentował 16 listopada 1904 roku.
Owen Richardson badał zjawisko emisji termoelektronowej sformułował wzór określający gęstość prądu emisji i otrzymał w 1928 roku nagrodę Nobla w dziedzinie fizyki za "prace dotyczące termoemisji elektronów, a w szczególności za odkrycie prawa nazwanego jego imieniem".
Prawo Richardsona
Rozgrzany metal lub tlenek metalu emituje elektrony. Gęstość prądu emisji J określona jest wzorem:
![]()
Gdzie A, zwana stałą Richardsona, określona jest wzorem:
![]()
T jest temperaturą w kelwinach,
W jest pracą wyjścia elektronu z metalu,
k jest stałą Boltzmana,
m i e to masa i ładunek elektronu,
h to stała Plancka.
Emisja elektronów to zjawisko fizyczne polegające na wyrzucaniu elektronów z przewodnika, półprzewodnika a w wyjątkowych przypadkach też z izolatorów do otoczenia. Do wyrzucenia elektronu z ciała potrzebna jest energia do pokonania przyciągania ciała w ilości równej lub większej niż praca wyjścia. W zależności od źródła energii dostarczanej emitowanym elektronom rozróżniane są:
Emisja termoelektronowa - źródłem energii elektronów jest energia kinetyczna ruchu cieplnego elektronów.
Jest najczęściej wykorzystywanym sposobem uzyskiwania elektonów - stosowana w niemal wszystkich typach lamp elektronowych.
Emisja fotoelektronowa - źródłem energii jest promieniowanie elektromagnetyczne np. światło, promieniowanie rentgenowskie.
Emisja wtórna - źródłem energii są uderzające w emitujący materiał cząstki, np. elektrony, protony
Emisja polowa - emisja pod wpływem bardzo silnego pola elektrycznego, na przykład na ostrzu (projektor elektronowy) lub w pobliżu ostrza poruszającego się nad ciałem (Skaningowy mikroskop tunelowy)
Egzoemisja - emisja pod wpływem różnych czynników, np. podczas deformowania, skrobania ciała, emisja pod wpływem światła o energii mniejszej od pracy wyjścia z ciała, które poddano wcześniej naświetlaniu promieniowaniem jonizującym.
Opracowanie wyników.
Charakterystyka
zależności prądu anodowego w funkcji prądu zwojnicy
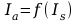 dla trzech stałych napięć anodowych
dla trzech stałych napięć anodowych
Dla Ua=2,5[V] Dla Ua=1,5[V]
|
|
Ja/10[mA] |
Js100[mA] |
|
Ja[mA] |
Js1000[mA] |
|
1 |
27,0 |
0,5 |
1 |
19,3 |
0,3 |
|
2 |
27,0 |
0,6 |
2 |
19,2 |
0,6 |
|
3 |
27,0 |
1,0 |
3 |
19,2 |
1,0 |
|
4 |
26,6 |
1,3 |
4 |
19,0 |
1,3 |
|
5 |
26,5 |
1,5 |
5 |
18,0 |
1,6 |
|
6 |
26,4 |
2,0 |
6 |
17,7 |
2,0 |
|
7 |
26,1 |
2,4 |
7 |
17,5 |
2,3 |
|
8 |
26,1 |
2,6 |
8 |
17,5 |
2,6 |
|
9 |
26,1 |
3,0 |
9 |
17,4 |
3,0 |
|
10 |
26,0 |
3,5 |
10 |
17,2 |
3,5 |
|
11 |
26,0 |
6,9 |
11 |
16,6 |
6,6 |
|
12 |
16,3 |
10,5 |
12 |
5,5 |
10,0 |
|
13 |
6,3 |
14,0 |
13 |
2,6 |
13,5 |
|
14 |
2,1 |
17,5 |
14 |
1,0 |
17,0 |
|
15 |
1,1 |
21,0 |
15 |
0,6 |
20,5 |
Wyznaczanie
z wykresów wartości prądów krytycznych
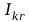 gdzie
gdzie
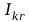 jest argumentem przypisanemu wartości
jest argumentem przypisanemu wartości
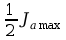 :
:
Dla
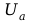 =2,5
[V],
=2,5
[V],
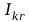 =
11,15
[A]
=
11,15
[A]
Dla
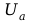 =12
[V]
,
=12
[V]
,
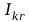 =8,33
[A]
=8,33
[A]
Obliczam
wartości
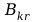 wykorzystując
wzór na natężenie pola w cewce Helmholtza:
wykorzystując
wzór na natężenie pola w cewce Helmholtza:
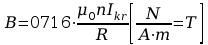
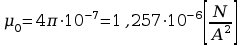

Dla
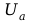 =2,5
[V],
=2,5
[V],

Dla
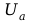 =1,5
[V],
=1,5
[V],

Obliczanie wartości ładunku właściwego elektronu e/m ze wzoru:
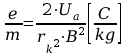
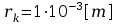 -
promień katody,
-
promień katody,
Dla
 =2,5
[V]
=2,5
[V]
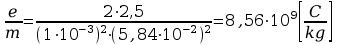
Dla
 =1,5
[V]
=1,5
[V]
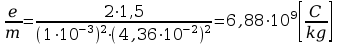
Wartość
średnią obliczam z wzoru:

Wyznaczanie odchylenia standardowego:

Wyznaczanie metodą Studenta – Fishera dla wartości e/m błąd prawdopodobny i maksymalny.
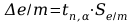
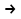 dla
dla
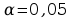
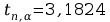
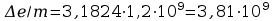
Wyszukiwarka
Podobne podstrony:
Teoria do I i II gr. anionów, ~FARMACJA, I rok, CHEMIA OGÓLNA I NIEORGANICZNA, Chemia końcowy z kati
teoria do weryfikacji elementów maszyn
teoria do egzaminu
Teoria do krzyżówek
Teoria do ćwiczeń laboratoryjnych, UTP Elektrotechnika, 2 semestr, Teoria obwodów, Laborki
TEORIA DO KRZYŻ., TEORIA DO KRZYŻOWEK
teoria do szeląd trzeba dokończyć pisać z , Studia - Inżynieria Środowiska, Hydraulika 1 i 2
teoria do 109, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria
TEORIA DO KRZYŻÓWEK, 160
metody projekcyjne teoria do prezentacji
analityczna teoria do 3 kartkowki
teoria do 6, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Teoria do projektu 3, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 2, Geodezja, od Donia -
WCY Teoria do cw 6, semestr 2, podstawy elektroniki i elektroniki
teoria do redoksów 2a, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie or
teoria do rozdz. 9, Rosyjski
Teoria do kolokwium, Inżynieria Środowiska Politechnika Śląska Rybnik, Ochrona Środowiska, Ochrona Ś
teoria do cwiczeń 05.11, semestr 1, Chemia, teoria