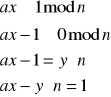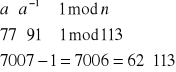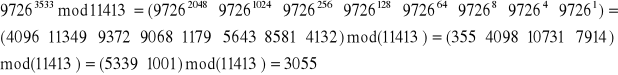Na początek takie krótkie zadanie do wykonania. Mamy dany prosty szyfr podstawieniowy:
PYX LODCXW PF PYID ETXDPIFO ID ZMXLW
A poniżej mamy 26 liter alfabetu angielskiego ułożonych w porządku od najczęściej używanej w angielskich tekstach:
e t a o i n s r h l d c u m f p g w y b v k x j q z
Należy rozszyfrować powyższy zaszyfrowany tekst. Należy to zrobić intuicyjnie podstawiając do szyfru odpowiednie litery i wyrazy korzystając z zasad gramatyki języka angielskiego, bo cały tekst jest w języku angielskim. Poprawnym rozwiązaniem będzie szyfr: THE ANSWER TO THIS QUESTION IS CLEAR.
Na dzisiejszych zajęciach z kolei zajmiemy się obliczaniem odwrotności modularnej. Załóżmy, że mamy jakąś liczbę naturalną n większą od 1 i jakieś a naturalne takie, że NWD(n, a) = 1. Oznacza to, że są to liczby względnie pierwsze, czyli takie, które nie mają wspólnych dzielników większych niż jeden. Wtedy istnieje 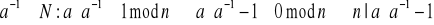
. Istnieje taka zasada, że jeśli liczba n w tej parze będzie liczbą pierwszą, to liczby n i a są względnie pierwsze. Przykładowo weźmy liczbę n = 113 i liczbę a = 77. Mamy wykazać, że rzeczywiście NWD(113, 77) = 1 i że liczby 113 i 77 są względnie pierwsze. Zatem na początek dokonamy małej przemiany tego równania, co już mieliśmy. Przyjmijmy, że x i y to liczby naturalne i x równe jest a do potęgi -1, czyli odwrotności a. Wówczas mamy zależność:
I teraz naszym zadaniem będzie znalezienie tych liczb x i y całkowitych, żeby tą jedynkę przedstawić jako taką kombinacje liniową x a i n. Podstawiamy wartości a i n do równania:
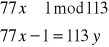
, gdzie x należy do przedziału od 1 do 112.
Skorzystamy najpierw z algorytmu Euklidesa i będziemy dzielić to 113 przez 77 z resztą chcąc udowodnić, czy rzeczywiście NWD(113, 77) = 1. I rozpisujemy:
I widzimy wyraźnie, że wyszła nam ta jedynka. A zatem potwierdziło się twierdzenie. Z tego ciągu wyprowadzimy rozkład, a potem z tego rozkładu odczytamy x i y. A zatem:
1 = 36 - 7 * 5 = 36 - 7 (77 - 2 * 36) = - 7 * 77 + 15 * 36 = - 7 * 77 + 15 (113 - 77) = 15 * 113 - 22 * 77, gdzie 113 to nasze n i 77 to nasze a. Teraz wystarczy podstawić to do równania:
Mamy nasze x. I na koniec liczymy nasze y:
Popatrzmy na następujący przykład. Niech p = 101, q = 113 i e = 3533. Zliczamy n = p * q = 101 * 113 = 11413. 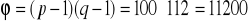
. Naszym zadaniem będzie policzenie d. A zatem wiedząc, że 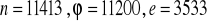
dokonujemy rozkładu algorytmem Euklidesa:
Mamy naszą jedynkę. Rozkładamy ją zatem:
1 = 5 - 2 * 2 = 5 - 2 (17 - 3 * 5) = -2 * 17 + 7 * 5. I tak dalej (rozkład należy dokończyć w domu). Po tym rozkładzie otrzymamy równość, że 1 = x * 11200 - y * 3533. I teraz nasze d będzie równe 11200 - y = 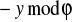
. Otrzymamy za d liczbę czterocyfrową. Kluczem publicznym będzie wówczas 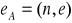
, zaś kluczem prywatnym będzie 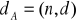
. Teraz natomiast przejdżmy do szyfrowania w RSA. Załóżmy, że mamy jakąś wiadomośc M (tekst jawny), jakiś szyfrogram C i przyjmijmy, że M = 9726 spełniający warunki, że 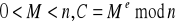
. Weźmy za n liczbę z poprzedniego zadania równą 11413, oraz liczbę e równą 3533. I teraz w jaki sposób obliczyć nasz szyfrogram C. Zgodnie z równaniem, czyli: 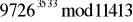
. Nie potęgujemy jednak tego, bo by to było nie możliwe, ale aby to obliczyć istnieje pewna zasada. Należy zastosować algorytm potęgowania modularnego. Polega on na tym, że najpierw rozkładamy liczbę 3533, czyli nasze e na potęgi liczby 2, czyli przyjmujemy, że 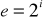
:
I teraz naszym zadaniem będzie obliczenie 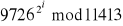
dla i od 0 do 11. I liczymy:
Ostatnim krokiem będzie rozpisanie. Z tego wyjdzie nam szukany szyfrogram C:
Aby sprawdzić, czy wyszedł dobry wynik, można poszukać klucza publicznego d takiego, że: 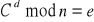
. D zliczamy na podstawie wzorów powyższych. I to niech będzie zadanie domowe.A teraz przejdźmy do kolejnego zadania. Należy wyznaczyć wartość liczbową tekstu jawnego M zaszyfrowanego algorytmem RSA przy pomocy klucza publicznego e = 13 wiedząc, że wartość liczbowa szyfrogramu c = 57, oraz wiedząc, że p = 11 i q = 7. Najpierw więc liczymy klucz publiczny (n, e). n liczymy ze wzoru p * q co daje 11 * 7 = 77. Więc mamy klucz publiczny (n, e) = (77, 13). Teraz kolej na wyznaczenie klucza prywatnego d = (n, d) = (77, d). Wiemy, że 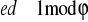
. Wielkość pomocnicza równa będzie w naszym przypadku 60. Mamy więc rozwiązać równanie 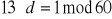
. Stosujemy tu algorytm Euklidesa do obliczenia d. I tak:
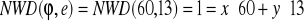
1 = 3 - 2 = 3 - (5 - 3) = -5 + 2 * 3 = - 5 + 2 (8 - 5) = 2 * 8 - 3 * 5 = 2 * 8 - 3 (13 - 8) = - 3 * 13 + 5 * 8 = - 3 * 13 + 5 (60 - 4 * 13) = 5 * 60 - 23 * 13. Więc x = 5 i y = - 23. Stąd d = - 23 mod 60 = 37. I mamy klucz prywatny d = (77, 37). Zdeszyfrujmy i sprawdźmy obliczenia. 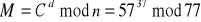
. Rozkładamy 37 na potęgi dwójki:
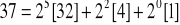
i liczymy 
. Do 5 bo jajwyższa potęga 2 to 5. I teraz:
Zatem się zgadza. Spróbujmy jeszcze zdeszyfrować obliczając szyfrogram korzystając ze wzoru 
. Rozpisujemy trzynastke na potęgi dwójki i mamy:
i liczymy teraz dla i = 0, 1, 2, 3:
I teraz: 
. Zatem się zgadza !
![]()